Wave energy converters in coastal structures

Introduction

Fig 1: Construction of a coastal structure.

Coastal works along European coasts are composed of very diverse structures. Many coastal structures are ageing and facing problems of stability, sustainability and erosion. Moreover climate change that produces especially sea level rise represents a new danger for them. Coastal dikes will be indeed exposed in Europe to waves with height greater than the design value, in particular all the structures built in shallow water where the depth imposes the maximal amplitude because of wave breaking.

These structures need therefore to be modernized and adapted on the one hand to climate change and on the other hand to increase of maritime traffic and size of container carriers.

This necessary adaptation will be costly but will constitute an opportunity to integrate converters of sustainable energy in the new maritime structures along the coasts and in particular in harbours. This initiative will contribute to the reduction of the greenhouse effect. Produced energy can be directly used for the energy consumption in harbour area and will reduce the carbon footprint of harbours by feeding the docked ships with green energy. Nowadays these ships use their motors to produce electricity power on board even if they are docked. Integration of wave energy converters in coastal structure will favour the emergence of the new concept of future harbour with zero emission.

Wave energy and wave energy flux

In a sea state, the time-mean wave energy density E per unit horizontal area on the water surface (J/m²) is the sum of kinetic and potential energy density per unit horizontal area. The potential energy density is equal to the kinetic energy both contributing half to the time-mean wave energy density E that is proportional to the wave height squared according to linear wave theory :

(1)

[math]E= \frac{1}{8} \rho g H_{m0}^2[/math]

g is the gravity and [math]H_{m0}^2[/math] the spectral estimate of significant wave height. As the waves propagate, their energy is transported. The energy transport velocity is the group velocity. As a result, the time-mean wave energy flux per unit crest length (W/m) perpendicular to the wave propagation direction, is equal to :

(2)

[math] P= Ec_{g}[/math]

with [math]c_{g}[/math] the group velocity (m/s). Due to the dispersion relation for water waves under the action of gravity, the group velocity depends on the wavelength λ (m), or equivalently, on the wave period T (s). Further, the dispersion relation is a function of the water depth h (m). As a result, the group velocity behaves differently in the limits of deep and shallow water, and at intermediate depths:

[math](\frac{\lambda}{20} \lt h \lt \frac{\lambda}{2})[/math]

Application for wave energy converters

For regular waves in deep water:

(3)

[math]c_{g} = \frac{gT}{4\pi} [/math] and [math]P_{w1} = \frac{\rho g^2}{32 \pi} H_{m0}^2 T[/math]

The time-mean wave energy flux per unit crest length is used as one of the main criteria to choose a site for wave energy converters. If local data are available ([math]H_{m0}^2 [/math], T) for a sea state through in-situ wave buoys for example, satellite data or numerical modelling, the last equation giving wave energy flux [math]P_{w1}[/math] gives a first estimation. Averaged over a season or a year, it represents the maximal energetic resource that can be theoretically extracted from wave energy. If the directional spectrum of sea state variance F (f,[math]\theta[/math]) is known with f the wave frequency (Hz) and [math]\theta[/math] the wave direction (rad), a more accurate formulation is used:

(4)

[math]P_{w2} = \rho g\int\int c_{g}(f,h)F(f,\theta) dfd \theta[/math]

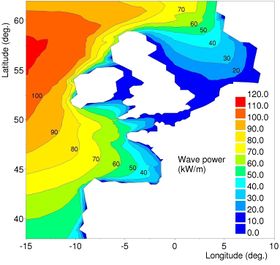
Fig 2: Time-mean wave energy flux along West European coasts .

It can be shown easily that equation (4) can be reduced to (3) with the hypothesis of regular waves in deep water. The directional spectrum is deduced from directional wave buoys, SAR images or advanced spectral wind-wave models, known as third-generation models, such as WAM, WAVEWATCH III, TOMAWAC or SWAN. These models solve the spectral action balance equation without any a priori restrictions on the spectrum for the evolution of wave growth.

From TOMAWAC model, the near shore wave atlas ANEMOC along the coasts of Europe and France based on the numerical modelling of wave climate over 25 years has been produced . Using equation (4), the time-mean wave energy flux along West European coasts is obtained (see Fig. 2). This equation (4) still presents some limits like the definition of the bounds of the integration. Moreover, the objective to get data on the wave energy near coastal structures in shallow or intermediate water requires the use of numerical models that are able to represent the physical processes of wave propagation like the refraction, shoaling, dissipation by bottom friction or by wave breaking, interactions with tides and diffraction by islands.

The wave energy flux is therefore calculated usually for water depth superior to 20 m. This maximal energetic resource calculated in deep water will be limited in the coastal zone:

• at low tide by wave breaking;
• at high tide in storm event when the wave height exceeds the maximal operating conditions;
• by screen effect due to the presence of capes, spits, reefs, islands,...

Technologies

According to the International Energy Agency (IEA), more than hundred systems of wave energy conversion are in development in the world. Among them, many can be integrated in coastal structures. Evaluations based on objective criteria are necessary in order to sort theses systems and to determine the most promising solutions.

Criteria are in particular:

1. the converter efficiency : the aim is to estimate the energy produced by the converter. The efficiency gives an estimate of the number of kWh that is produced by the machine but not the cost.
2. the converter survivability : the capacity of the converter to survive in extreme conditions. The survivability gives an estimate of the cost considering that the weaker are the extreme efforts in comparison with the mean effort, the smaller is the cost.

Unfortunately, few data are available in literature. In order to determine the characteristics of the different wave energy technologies, it is necessary to class them first in four main families .

Overtopping with low-head hydraulic turbine	Submerged oscillating bodies with hydraulic motor, hydraulic turbine, linear electrical generator.
Floating oscillating bodies with hydraulic motor, hydraulic turbine, linear electrical generator.	Oscillating water column with water turbine.
Fig 3: The various wave energy technologies

An interesting result is that the maximum average wave power that a point absorber can absorb [math]P_{abs} (W)[/math] from the waves does not depend on its dimensions . It is theoretically possible to absorb a lot of energy with only a small buoy. It can be shown that for a body with a vertical axis of symmetry (but otherwise arbitrary geometry) oscillating in heave the capture (or absorption) width [math]L_{max} (m)[/math] is as follows :

(5)

[math]L_{max} = \frac{P_{abs}}{P_{w}} = \frac{\lambda}{2\pi}[/math] or [math]1 = \frac{P_{abs}}{P_{w}} \frac{2\pi}{\lambda}[/math]

References

The main author of this article is Sergent, Philippe With contributions by: François Bouttes, Bertrand Michard, Alain Clément, Aurélien Babarit, Virginie Baudry, Michel Benoit and Giovanni Mattarolo For other articles by this author see Category:Articles by Sergent, Philippe