Difference between revisions of "Swash zone dynamics"
Dronkers J (talk | contribs) (Created page with "==Introduction== Image: BaldockFig1.jpg|thumb|440px|left|Figure 1. Definition sketch for the nearshore littoral zone (swash zone width exaggerated). After <ref> Elfrink, B....") |
Dronkers J (talk | contribs) |
||
| Line 154: | Line 154: | ||
{{author | {{author | ||
| − | |AuthorID= | + | |AuthorID=34603 |
|AuthorFullName=Tom Baldock | |AuthorFullName=Tom Baldock | ||
|AuthorName= Tom Baldock}} | |AuthorName= Tom Baldock}} | ||
Revision as of 12:03, 1 June 2017
Contents
Introduction
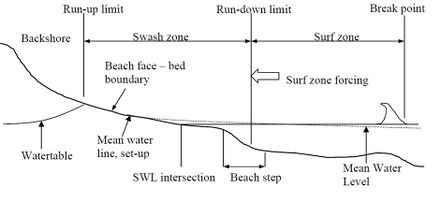
The swash zone forms the land-ocean boundary at the landward edge of the surf zone, where waves runup the beach face (figures 1, 2). It is perhaps the region of the ocean most actively used by recreational beach users and, being very visible, is the region of the littoral zone most associated with beach erosion and the impacts of climate change. The landward edge of the swash zone is highly variable in terms of geomorphology, and may terminate in dunes, cliffs, marshes, ephemeral estuaries and a wide variety of sand, gravel, rock or coral barriers. This influences the exchange of sediment between the land and ocean, which ultimately forms the coastline.
In terms of coastal processes and coastal protection, a large part of the littoral sediment transport occurs in the swash zone, both cross-shore and longshore, which influences beach morphology, and beach erosion and beach recovery during and after storms. Wave runup is an important factor in the design of coastal protection and also generates hazards for beach users, and is the dominant process leading to the erosion of coastal dunes. Swash hydrodynamics also influence the ecology of the intertidal zone and groundwater levels in sub-aerial littoral beaches and low lying islands, which is often critical for freshwater water supply on islands and atolls [2].
Characteristics of the swash zone
The hydrodynamic processes in the swash zone are characterised by very different types of fluid flow compared to the open ocean and surf zone, as illustrated in figure 2, where the strongly orbital motion of waves is transformed into flow parallel to the bed (velocity [math]V[/math]), usually in thin shallow sheets (thickness [math]d[/math]). In terms of fluid mechanics, the key difference is the occurrence of supercritical flow in the swash zone, where the Froude number,[math]V/ \sqrt{gd}[/math], is greater than 1, which has important implications for the nature of the flow. Other important distinctions are that friction becomes more important in controlling aspects of the shallow flow in the swash zone than in the surf zone, and that turbulence and sediment transport in the swash zone is generated locally in the swash zone and advected into the swash zone from the surf zone. A key feature of both the hydrodynamics and sediment dynamics in the swash zone is intermittency, where the extent and degree of inundation of the swash zone varies over different timescales, from orders of seconds and tidal periods to years and decades. This is a challenge for coastal scientists, both in terms of measurement and modelling of the physical processes. For the purposes of this summary, the swash zone will be considered as the region of the beach face exposed to the atmosphere over wind, swell and infragravity wave durations, i.e., seconds to a few minutes.
The characteristics of the swash zone hydrodynamics and sediment transport are governed by the inner surf zone and the underlying beach, with feedback of course between the morphology and hydrodynamic processes. The beach slope is a controlling parameter [3]. On dissipative beaches, with wide surf zones, most of the wind wave and swell energy is dissipated seaward of the swash zone. Therefore, swash processes are dominated by those due to long, or infragravity, waves, which are frequently non-breaking standing waves (figure 2a). On intermediate and reflective beaches, short wave energy reaches the beach face in the form of bores or shore-breaks, which collapse at the beach, initiating a runup motion characterised by a thin sheet of water with a rapidly propagating wave tip which is analogous to a dam-break flow over a dry bed (figure 2b). This sheet of water is slowed by gravity and friction until the flow reverses and forms another shallow flow seaward, the backwash. On coarse grained sand and gravel beaches a significant volume of the uprush and some of the backwash may percolate into the beach, reducing the volume of water in the surface backwash flow. These two distinct types of swash zone make modelling hydrodynamic processes difficult, since parametric models rely on similarity of processes, and therefore phase resolving models of the whole surf zone, or at least the inner surf zone, are required if the details of the hydrodynamics are required. Fortunately some processes are modelled very well by parametric models, perhaps more accurately than phase-resolving models, particularly wave runup.
Wave runup and overtopping
Wave runup is perhaps the most important aspect of swash zone flows. While the motion of the water volume as a whole may be considered as runup, conventionally wave runup refers to the landward limit of the swash motion on the beach face, usually defined vertically above the ocean level. The runup and rundown of the shoreline is referred to as the swash excursion or oscillation. A typical plot of the shoreline motion is shown in figure 3.
Remarkably, the maximum runup is still most reliably described by a simple empirical parametric formula, which is perhaps one of the oldest regularly in use, proposed by Hunt (1959). Despite numerous variations, the underlying scaling still holds over a very large range of wave conditions, both in the laboratory and field. The scaling for runup proposed by Hunt [4] is:
[math]R_{max}=\xi H_0 = \tan \beta \sqrt{H_0 L_0} , \qquad (1)[/math]
where [math]\xi[/math] is the surf similarity parameter, or Iribarren number ([math]\xi =\tan\beta / \sqrt{H_0/L_0})[/math] and [math]H_0, L_0[/math] and [math]\beta[/math] are offshore wave height, wave length and the swash zone beach face slope, respectively. This is strictly only applicable for monochromatic waves and the maximum runup. However, the same formulation has been widely used to describe random wave runup, using appropriate statistical parameters to describe the wave conditions. This parameter is usually the runup elevation exceeded by 2% of the waves, [math]R_{2\%}[/math]. The most widely used derivative of Hunt's formula is perhaps due to Stockdon et al. [5], which also allows for a contribution from infragravity waves:
[math] R_{2/%} = 1.1 \; \left( 0.5 \sqrt{H_s L_p \; (0.563 \beta^2 + 0.004)} +0.35 \; \beta \sqrt{H_s L_p} \right) , \qquad \xi_p \ge 0.3 , \qquad (2)[/math]
[math] R_{2/%}= 0.43 \; \beta \sqrt{H_s L_p} , \qquad \xi_p \lt 0.3 , \qquad (3)[/math]
where the term [math]0.35 \; \beta \sqrt{H_s L_p}[/math] represents the setup, [math]H_s[/math] is the deep water significant wave height, and [math]L_p[/math] is the wavelength corresponding to the deep water peak wave period, [math]T_p[/math]. Atkinson et al. [6] compared a number of recent runup formulations to measurements from a range of beaches and concluded that the models generally predict runup with errors of order [math]\pm 25 \%[/math].

Swash-swash interactions occur through the overtaking of a swash uprush by the following bore or during the collision of the backwash flow with the next uprush. The magnitude, or vertical excursion, of the swash oscillations, from rundown position to runup, is strongly influenced by interaction between wave uprush and backwash, with the period of the incident waves also controlling the period of the swash oscillations at swell and wind wave frequencies [8]. Hence, given a finite time for the uprush and backwash to occur, there is a finite magnitude for a swash oscillation at a given frequency on a given beach slope if the motion is solely controlled by gravity. This leads to swash saturation, where an increase in incident wave height does not increase the magnitude of the swash oscillations. This can be parameterised for individual events, or through a spectral representation.
For non-breaking monochromatic waves, this limit is given by Miché [9]:
[math]\varepsilon_s=\frac{a_s \omega^2}{g \beta^2} = 1 , \qquad (4)[/math]
where [math]a_s[/math] is the vertical amplitude of the shoreline motion, [math]\omega[/math] is the angular wave frequency ([math]=2 \pi f[/math] - where [math]f[/math] is the wave frequency), [math]g[/math] the gravitational acceleration and [math]\beta[/math] the beach slope. This assumes a saturated surf zone and, based on the limiting amplitude for monochromatic unbroken standing waves, [math]\varepsilon \approx 1[/math]. For swash initiated by breaking wave bores, Baldock and Holmes [10] derived a theoretical value [math]\varepsilon \approx 2.5[/math], where saturation is controlled by swash-swash interaction as opposed to surf zone saturation. Spectra of the shoreline oscillations also indicate saturation at higher frequencies, with a typical roll-off in the energy density that is proportional to [math]f^{-4}[/math], which is also evident from equation 4. Huntley et al. [11] proposed a uniform spectral form for saturated swash spectra, but variations occur due to different surf zone conditions (figure 4).

When the runup exceeds the elevation of the crest of a structure, beach berm or dunes, wave overtopping or wave overwash occurs. This process is very important in building beach berms higher, in association with the spring-neap tidal cycle, but also leads to coastal flooding and inundation of the backshore region. The geomorphology of barrier islands and gravel barriers is strongly dependent on swash overtopping, and breaching of these systems by landward transport of sediment during the overtopping can lead to rapid and potentially catastrophic failure of protective coastal barriers (figure 5). The response of coastlines to sea level rise is also be influenced by swash overtopping and sediment overwash, which increases recession in comparison to the classical Bruun Rule [13]. A combination of parametric modelling and numerical techniques is required to model these scenario [14]
Swash zone hydrodynamics

Swash zone flows have several features that differ from those in the surf zone, but this is dependent on the dominant wave conditions in the inner surf zone as noted above. Many key characteristics again depend on the Iribarren number [17]. For infragravity standing long waves, the variation in flow depth and flow velocity at a point is relatively symmetrical during uprush and backwash. Short wave bores generate more asymmetrical flows, with the maximum velocity occurring at the start of inundation, with a rapid rise to the maximum depth, with an almost linear deceleration to flow reversal, and a correspondingly similar uniform acceleration in the backwash, at least until the flow becomes very shallow, when friction retards the flow significantly. A key aspect of these flows is diverging flow, which means the swash lens thins rapidly.
Runup and backwash velocities in the field reach 2-5 m/s, which are generally larger than those in the surf zone. The runup durations are typically shorter than the backwash duration, and the backwash depths are shallower than during the uprush, and therefore the velocity moments tend to be skewed offshore, which has important implications for the sediment dynamics [18]. The asymmetry is however affected by the mass and momentum advected into the swash zone, which depends on the flow in the inner surf zone. Self-similar solutions for different boundary conditions are presented by Guard and Baldock [16], following the work of Peregrine and Williams [15], figure 6. These indicate the fundamental nature of the hydrodynamics, which comprise of a near parabolic motion of the shoreline (due to gravity being the dominant process) and a saw-tooth shaped variation in velocity with time, which decreases at a near linear rate from the peak velocity, which occurs as the shoreline passes a given location. The water surface slope dips seaward for nearly the whole swash cycle, i.e. the total fluid acceleration is offshore throughout the swash cycle.
This results in a key difference between the surf zone and swash zone bed boundary conditions, namely that there is generally little phase lag between velocity and the bed shear stress in the swash zone, i.e. maxima in bed shear stress occur close to the instants of maxima in velocity. Close to the time of flow reversal, the flow near the bed does however reverse prior to the flow higher in the water column, due to the adverse pressure gradient during the uprush [19]. The boundary layer is thinnest at the seaward edge of the swash zone during uprush, and grows following the flow up the beach. The boundary layer largely vanishes at flow reversal, and again grows from the bed as the flow recedes. Accounting for such processes in sediment transport models remains to be tackled.
There are several sources of turbulence in the swash zone. In the runup, turbulence is advected from the inner surf zone, which combines with further generation of turbulence at the bed. The boundary layer is evolving, generally increasing in thickness and may become depth limited. During the backwash turbulence generation occurs mainly at the bed, with swash-swash interactions generating further turbulence as the next wave arrives. Overall, the high turbulence near the bed leads to high bed shear stresses and the potential for high concentrations of suspended sediment transport [21].
Friction plays a large role in controlling the shoreline motion, with friction factors based on conventional fluid mechanics principles typically in the range [math]0.02\lt f\lt 0.1[/math]. Friction effects are strongest when the flow is shallowest, at the swash tip, reducing runup excursions, and late in the backwash, so the shoreline recedes more slowly. Simple models, comprising of a ballistic motion plus friction, describe the shoreline motion reasonably well, although details are missing [22][23]. Inclusion of friction effects in the internal flow requires numerical modelling at present, or the use of integral models which can avoid the uncertainty in the treatment of friction at the shoreline [24]. However, recent results suggest that the effects of friction on the internal flow are small compared to the effects at the swash tip. For example, figure 7 shows a method of characteristics solution for the swash flow with and without friction. The numerical results indicate that the two solutions are similar when water is present, which is interesting given the significant effect of friction on the location of the shoreline. The reason is the supercritical nature of the flow, which is a particular feature of the swash zone. This means that the large change in the shoreline position due to friction does not significantly affect the flow seaward of the shoreline until the flow becomes subcritical, which does not occur until late in the uprush. Similarly, the supercritical nature of the backwash flow means that the changes to the shoreline position further landward cannot significantly affect flow further seaward. Thus, the supercritical nature of the swash flow means that the significant changes in shoreline position do not significantly affect the flow in the interior of the swash lens.
Sediment transport mechanics

Cross-shore sediment transport in the swash zone generally occurs as a combination of bed load under sheet flow conditions, with a flat bed, plus an additional component of suspended load, generated locally and advected into the swash zone by surf zone bores. For the bed load, the Meyer-Peter and Muller [26] formulation, or derivatives, generally perform well with calibration, i.e. determining the transport coefficient and friction factor remain problematic. In these models, the transport is typically a function of the velocity cubed. The relative balance between bed load, which is generated locally, and suspended load depends on the sediment grain size, and also on the quantity of sediment advected into the swash zone from the inner surf zone (figure 8). This can be considerable, and affects the distribution of suspended load across the swash zone. While the basic sediment transport equations still apply, model-data comparisons are lacking, particularly close to the bed where suspended sediment concentrations are largest.

In simple [math]u^3[/math] type sediment transport models the asymmetry of the flow tends to export sediment from the swash zone. In reality, this is balanced by the suspended sediment imported and advected into the swash zone from the inner surf [25], the distribution of which is illustrated in figure 9. Measurement of suspended sediment in the backwash remains a challenge, and is difficult to separate from bed-load. The quantity of suspended load entering the swash zone affects the net deposition pattern, and hence zones of erosion or accretion, as illustrated by Pritchard and Hogg [27]. Data is still lacking in the field to reliably quantify this process, which is complicated by sediment suspended by swash-swash interactions and the influence of turbulence in the inner surf zone, which is significant [28]. The infiltration and exfiltration of water into the beach during swash flows is an important contributor to groundwater processes, particularly on coarse grain beaches, and also influences sediment transport [29].
The mechanics of longshore sediment transport in the swash zone are well-understood in principle, but data and modelling is limited, despite the clear presence of a significant contribution to the total longshore transport in the littoral zone. In the swash zone the flow direction during both runup and rundown has a longshore component under oblique waves (the usual case). The boundary between the surf and swash zone is also an active region of longshore transport, particularly on steep cobble or coral beaches, where sediment may also move offshore into the inner surf zone, then alongshore, and then back onshore as the wave conditions or tide change [30]. While the relative importance of longshore transport in the swash zone compared to the surf zone is greater during milder wave conditions than during storms, longshore sediment transport in the swash zone may account for up to 50% of the total longshore transport [31]. Longshore transport in the swash zone is also relatively more important on steep beaches and where small oblique waves break frequently at the shoreline, e.g., in estuary mouths and landward of lagoons behind fringing and barrier reefs.
Morphodynamics
The evolution of the beach face in the swash zone is controlled by the sediment fluxes across the boundaries, both longshore and cross-shore. Thus, the morphology is influenced by the presence of dunes, cliffs and hard structures at the landward extent of the beach, by conditions in the inner surf one, notably bars, rip cells, beach steps, and by lateral boundaries such as groynes, breakwaters and estuary mouths. While the general processes are again well understood, and similar to those applied for littoral transport in the surf zone, the details of dune erosion, barrier degradation and progradation and the short and long term balance of sediment deposition and erosion remain a challenge [32]. For example, rates of deposition and erosion vary significantly on wave-by-wave time scales, wave group time-scales, and tidal time-scales, plus seasonal and annual changes due to variations in wave and wind climate. Further, while the active swash zone is usually relatively plane (excluding dunes), feedback between morphology and hydrodynamics does lead to more complex morphology such as Beach Cusps. Varying tides also lead to the formation of beach ridges and berms at different elevations, which complicate the overall topography. Dunes act as significant sources and sinks of sediment that control swash zone morphodynamics and that of the whole beach, and are essential in developing the sediment budget for the whole beach. A further aspect is the influence of vegetation, which can provide important stabilising mechanisms for dunes. The upper beach and swash zone is where the impacts of sea level rise will be most visible, with loss of the upper beach if the coastline cannot recede landward.
Measurement techniques
Research on swash zone processes is both assisted and hindered by the nature of the swash. The beach face is generally accessible for deployment of instruments, particularly with the aid of large tides, it is close to the shore and associated infrastructure, and much wave energy has been dissipated in the surf zone. However, flows are very shallow and also intermittent, making measurements over the depth difficult and time-averaging complex. In terms of in-situ instruments, the shoreline motion can be measured by runup wires or point instruments such as pressure sensors or ultrasonic sensors, flow velocity with electromagnetic or acoustic instruments, and morphology changes with standard survey techniques or ultrasonic sensors. To tackle larger scales and to avoid in-situ measurements and to sample over longer time-scales, remote sensing by video has adopted techniques first developed for the surf zone by Aagaard and Holm [33] to determine friction factors [23], runup [5] and internal kinematics [34]. Shore-mounted LIDAR is becoming a promising tool for high resolution and long term monitoring [35], figure 10. However, both these techniques suffer from loss of resolution in the thinning backwash, and do not provide flow velocity with any degree of reliability. Sediment transport measurements using sediment traps [36][37] still provide the most reliable measure of total load transport rates in the field, supplemented by sediment transport rates derived from morphological measurements through sediment continuity, which can be particularly useful during overwash events. Both techniques require predominantly cross-shore transport.
Related articles
References
- ↑ Elfrink, B. and T. Baldock (2002). Hydrodynamics and sediment transport in the swash zone: a review and perspectives. Coastal Engineering 45: 149-167
- ↑ Nielsen P., 1999. Groundwater dynamics and salinity in coastal barriers. J. Coastal Res., 15: 732-740.
- ↑ Guza, R. T., Thornton, E. B. and Holman, R. A., 1984. Swash on steep and shallow beaches. Proc. 19th Int. Conf. Coastal Eng., ASCE, 708-723.
- ↑ Hunt, I.A., 1959. Design of sea-walls and breakwaters. Transactions of the American Society of Civil Engineers, 126: 542-570.
- ↑ 5.0 5.1 Stockdon, H. F., Holman, R. A., Howd, P. A. & Sallenger JR, A. H. 2006. Empirical parameterization of setup, swash, and runup. Coastal Engineering, 53, 573-588.
- ↑ Atkinson, A.L., Power, H.E., Moura, T., Hammond, T., Callaghan, D.P. and Baldock, T.E., 2017. Assessment of runup predictions by empirical models on non-truncated beaches on the south-east Australian coast. Coastal Engineering, 119: 15-31.
- ↑ Hughes, M. G., T. Aagaard, T. E. Baldock and H. E. Power, 2014. Spectral signatures for swash on reflective, intermediate and dissipative beaches. Marine Geology 355: 88-97.
- ↑ Holman, R. A. 1986. Extreme value statistics for wave runup on a natural beach. Coastal Engineering, 9: 527-544.
- ↑ Miché, R., 1951. Le pouvoir réfléchissant des ouvrages maritimes exposés à l'action de la houle. Ann. Ponts et Chaussees, 121: 285-319.
- ↑ Baldock T. E. and Holmes P., 1999. Simulation and prediction of swash oscillations on a steep beach. Coastal Engineering, 36: 219-242.
- ↑ Huntley, D. A., R. T. Guza and A. J. Bowen, 1977. Universal form for shoreline runup spectra. Journal of Geophysical Research-Oceans and Atmospheres 82: 2577-2581.
- ↑ Donnelly, C., N. Kraus and M. Larson, 2006. State of knowledge on measurement and modeling of coastal overwash. Journal of Coastal Research 22: 965-991.
- ↑ Rosati, J. D., R. G. Dean and T. L. Walton, 2013. The modified Bruun Rule extended for landward transport. Marine Geology 340: 71-81.
- ↑ Roelvink, D., Reniers, A., Van Dongeren, A.P., de Vries, J.V.T., McCall, R. and Lescinski, J., 2009. Modelling storm impacts on beaches, dunes and barrier islands. Coastal engineering, 56: 1133-1152.
- ↑ 15.0 15.1 15.2 Peregrine, D. H. and S. M. Williams, 2001. Swash overtopping a truncated plane beach. Journal of Fluid Mechanics 440: 391-399.
- ↑ 16.0 16.1 Guard, P. A. and T. E. Baldock, 2007. The influence of seaward boundary conditions on swash zone hydrodynamics. Coastal Engineering 54: 321-331.
- ↑ Roos, A. and Battjes, J.A., 1977. Characteristics of flow in runup of periodic waves. Proc. 15th International Conference on Coastal Engineering, ASCE, pp. 781-795
- ↑ Raubenheimer, B., R. T. Guza, S. Elgar and N. Kobayashi, 1995. Swash on a gently sloping beach. Journal of Geophysical Research-Oceans 100(C5): 8751-8760.
- ↑ Kikkert, G. A., T. O'Donoghue, D. Pokrajac and N. Dodd, 2012. Experimental study of bore-driven swash hydrodynamics on impermeable rough slopes. Coastal Engineering 60: 149-166.
- ↑ Deng, X., H. Liu, Z. Jiang and T. E. Baldock, 2016. Swash flow properties with bottom resistance based on the method of characteristics. Coastal Engineering 114: 25-34
- ↑ Puleo, J. A., R. A. Beach, R. A. Holman and J. S. Allen, 2000. Swash zone sediment suspension and transport and the importance of bore-generated turbulence. Journal of Geophysical Research-Oceans 105(C7): 17021-17044.
- ↑ Hughes M. G., 1995. Friction factors for wave uprush. J. Coastal Res., 13: 1089-1098
- ↑ 23.0 23.1 Puleo, J. A. and K. T. Holland, 2001. Estimating swash zone friction coefficients on a sandy beach. Coastal Engineering 43: 25-40
- ↑ Archetti, R. and M. Brocchini, 2002. An integral swash zone model with friction: an experimental and numerical investigation. Coastal Engineering 45: 89-110.
- ↑ 25.0 25.1 25.2 Hughes, M. G., T. Aagaard and T. E. Baldock, 2007. Suspended sediment in the swash zone: Heuristic analysis of spatial and temporal variations in concentration. Journal of Coastal Research 23: 1345-1354.
- ↑ Meyer-Peter, E. and Müller, R., 1948. Formulas for bed-load transport. Proc. IAHR, Stockholm
- ↑ Pritchard, D. and A. J. Hogg, 2005. On the transport of suspended sediment by a swash event on a plane beach. Coastal Engineering 52: 1-23
- ↑ Butt, T., P. Russell, J. Puleo, J. Miles and G. Masselink, 2004. The influence of bore turbulence on sediment transport in the swash and inner surf zones. Continental Shelf Research 24(7-8): 757-771.
- ↑ Turner, I.L. and G. Masselink, 1998. Swash infiltration-exfiltration and sediment transport. Journal of Geophysical Research, 103(C13): 30,813-30,824
- ↑ Kench, P. S., E. Beetham, C. Bosserelle, J. Kruger, S. M. L. Pohler, G. Coco and E. J. Ryan, 2017. Nearshore hydrodynamics, beach face cobble transport and morphodynamics on a Pacific atoll motu. Marine Geology 389: 17-31.
- ↑ Kamphuis J. W., 1991. Alongshore sediment transport rate distribution. Coastal Sediments '91 Conference, ASCE, 170-183.
- ↑ Masselink, G. and J. A. Puleo (2006). Swash-zone morphodynamics. Continental Shelf Research 26(5): 661-680
- ↑ Aagaard, T. and J. Holm, 1989. Digitization of wave runup using video records. Journal of Coastal Research 5: 547-551.
- ↑ Power, H. E., R. A. Holman and T. E. Baldock, 2011. Swash zone boundary conditions derived from optical remote sensing of swash zone flow patterns. Journal of Geophysical Research, Oceans 116, C06007, doi:10.1029/2010JC006724
- ↑ Blenkinsopp, C. E., M. A. Mole, I. L. Turner and W. L. Peirson, 2010. Measurements of the time-varying free-surface profile across the swash zone obtained using an industrial LIDAR. Coastal Engineering 57(11-12): 1059-1065.
- ↑ Horn, D. P. and T. Mason, 1994. Swash zone sediment transport modes. Marine Geology 120(3-4): 309-325.
- ↑ Masselink, G. and M. Hughes (1998). Field investigation of sediment transport in the swash zone. Continental Shelf Research 18(10): 1179-1199
Please note that others may also have edited the contents of this article.
|




