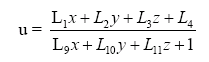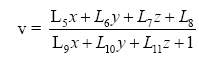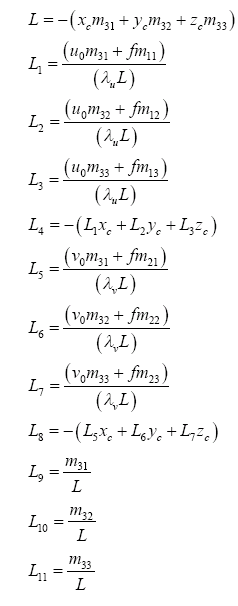Difference between revisions of "Argus standard image processing"
| Line 1: | Line 1: | ||
== Geo-referencing of oblique video data == | == Geo-referencing of oblique video data == | ||
| − | Quantification of image features like sand bars, shorelines and foam patterns demands the conversion of image coordinates to field coordinates . This conversion depends on the camera location , the camera orientation defined through three camera angles, namely the tilt, the azimuth and the roll, and the effective focal length, which directly relates to the camera horizontal field of view. The angles , and represent the rotation with regard to the vertical z-axis, the orientation in the horizontal -plane and the rotation of the focal plane with respect to the horizon, respectively. The transformation of field to image coordinates is thus a rotation about three successive angles , and and can be expressed by the linearised version of the collinearity equations, following standard photogrammetric procedures, as follows (Holland et al., 1997): | + | Quantification of image features like sand bars, shorelines and foam patterns demands the conversion of image coordinates to field coordinates . This conversion depends on the camera location , the camera orientation defined through three camera angles, namely the tilt, the azimuth and the roll, and the effective focal length, which directly relates to the camera horizontal field of view. The angles , and represent the rotation with regard to the vertical z-axis, the orientation in the horizontal -plane and the rotation of the focal plane with respect to the horizon, respectively. The transformation of field to image coordinates is thus a rotation about three successive angles , and and can be expressed by the linearised version of the collinearity equations, following standard photogrammetric procedures, as follows (Holland et al., 1997, [[Argus literature]]): |
| − | [[Image:Equation1.png|thumb|250px|centre]] | + | [[Image:Equation1.png|thumb|250px|centre|Equation 1]] |
and | and | ||
| − | [[Image:Equation2.png|thumb|250px|centre]] | + | [[Image:Equation2.png|thumb|250px|centre|Equation 2]] |
The coefficients L1 to L11 are linear functions of the camera orientation ( , , ), the | The coefficients L1 to L11 are linear functions of the camera orientation ( , , ), the | ||
camera position and the effective focal length ( ). The inverse transformation from image to field coordinates results in a system of two equations with three unknowns. The z-coordinates are assumed in this transformation to match a certain horizontal reference level or the tidal water level. | camera position and the effective focal length ( ). The inverse transformation from image to field coordinates results in a system of two equations with three unknowns. The z-coordinates are assumed in this transformation to match a certain horizontal reference level or the tidal water level. | ||
| − | + | [[Image:imiageVSrealworld.png|thumb|350px|centre|Relation between image (u,v) and real world (x,y,z) co-ordinates]] | |
| − | |||
| − | Standard photogrammetric procedures (Holland et al., 1997) enable the transformation from real world coordinates (x,y,z) to image coordinates (u,v) on the basis of the collinearity equations (Eq | + | Standard photogrammetric procedures (Holland et al., 1997, [[Argus literature]]) enable the transformation from real world coordinates (x,y,z) to image coordinates (u,v) on the basis of the collinearity equations (Eq. 1 and 2) .The latter contain 11 coefficients L1-L11, which are described as |
| − | + | [[Image:Equation3.png|thumb|250px|centre|Equation 3]] | |
| + | In Eq. 3, (x,y,z) are the camera xyz-coordinates, (u0,v0) are the image center uv-coordinates, f is the effective focal length and λu and λv are the horizontal and vertical scale factors. The m-coefficients describe the successive rotations around the azimuth , tilt and roll , | ||
| − | + | [[Image:Equation4.png|thumb|250px|centre|Equation 4]] | |
| − | |||
| − | |||
The theoretical formulations presented here are valid for use with distortion-free lenses. Owing to the incorporation of λu and λv, the formulations embody a correction for the slightly non-squareness of individual pixels. The latter is induced by a minor difference in sampling frequency between the camera and image acquisition hardware, which causes a minor mismatch between the number of horizontal picture elements at the camera CCD and the number of columns at the image frame buffer, where the image processing system stores the video data. | The theoretical formulations presented here are valid for use with distortion-free lenses. Owing to the incorporation of λu and λv, the formulations embody a correction for the slightly non-squareness of individual pixels. The latter is induced by a minor difference in sampling frequency between the camera and image acquisition hardware, which causes a minor mismatch between the number of horizontal picture elements at the camera CCD and the number of columns at the image frame buffer, where the image processing system stores the video data. | ||
| − | |||
== Argus Database == | == Argus Database == | ||
Revision as of 15:59, 4 April 2007
Geo-referencing of oblique video data
Quantification of image features like sand bars, shorelines and foam patterns demands the conversion of image coordinates to field coordinates . This conversion depends on the camera location , the camera orientation defined through three camera angles, namely the tilt, the azimuth and the roll, and the effective focal length, which directly relates to the camera horizontal field of view. The angles , and represent the rotation with regard to the vertical z-axis, the orientation in the horizontal -plane and the rotation of the focal plane with respect to the horizon, respectively. The transformation of field to image coordinates is thus a rotation about three successive angles , and and can be expressed by the linearised version of the collinearity equations, following standard photogrammetric procedures, as follows (Holland et al., 1997, Argus literature):
and
The coefficients L1 to L11 are linear functions of the camera orientation ( , , ), the camera position and the effective focal length ( ). The inverse transformation from image to field coordinates results in a system of two equations with three unknowns. The z-coordinates are assumed in this transformation to match a certain horizontal reference level or the tidal water level.
Standard photogrammetric procedures (Holland et al., 1997, Argus literature) enable the transformation from real world coordinates (x,y,z) to image coordinates (u,v) on the basis of the collinearity equations (Eq. 1 and 2) .The latter contain 11 coefficients L1-L11, which are described as
In Eq. 3, (x,y,z) are the camera xyz-coordinates, (u0,v0) are the image center uv-coordinates, f is the effective focal length and λu and λv are the horizontal and vertical scale factors. The m-coefficients describe the successive rotations around the azimuth , tilt and roll ,
The theoretical formulations presented here are valid for use with distortion-free lenses. Owing to the incorporation of λu and λv, the formulations embody a correction for the slightly non-squareness of individual pixels. The latter is induced by a minor difference in sampling frequency between the camera and image acquisition hardware, which causes a minor mismatch between the number of horizontal picture elements at the camera CCD and the number of columns at the image frame buffer, where the image processing system stores the video data.
Argus Database
The Argus data base of meta information (hereafter referred to as argusDB) is a key-component of the Argus Runtime Environment. Without argusDB, no quantitative interpretation of image features would be possible. The argusDB contains all information needed to quantitatively interpret Argus video images. This concerns the characteristics of the local site, video station, image processor, cameras applied, the available ground control points and geometry solutions, etc. All meta information is accessible on the basis of the Argus image filename (that is: epochtime, name of the station and camera number). The different components of argusDB are all inter-connected. For instance, on the basis of the site identifier, all video stations available at that site can found. On the basis of the station identifier, all cameras of that station can be found. On the basis of a camera identifier, all geometry solutions available for that camera can be found, etc. Using the epochtime of interest as an additional constraint yields a unique geometry solution, etc.
Merging images
Panoramic and plan view merged images can be composed by geo-referencing the images from all the cameras of an Argus station. Plan view images enable the measurement of length scales of morphological features like breaker bars and the detection of rip currents. A very useful post-processing tool is the Argus Merge Tool which enables to rectify and join together single time averaged Argus images. This results in a plan view of the nearshore zone (Fig.).
Fig.: Merged image
The bright regions indicate regions of intense wave breaking hence the location of shallow water depth. In this way, morphologic features like the shoreline and breaker bars can easily be identified. Within the Argus merge tool it is possible to specify the condition at which moments images are collected to create a merged image. The condition can either be a tidal level or a wave height, both user-defined. Specifying a condition with wave heights bigger than 1.5 m produces merged images on which the bars are clearly visible by the smooth white bands at locations with a lot of wave breaking. These images are appropriate to analyse the behaviour of bars. When a low-tide level condition is specified, for example NAP -0.60 m, the rendered merged images are very useful to analyse the morphological features of the intertidal beach.