Difference between revisions of "Artificial reefs"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 101: | Line 101: | ||
==See also== | ==See also== | ||
| − | :[[Natural barriers]] | + | :[[Natural shore protecting barriers]] |
:[[Detached breakwaters]] | :[[Detached breakwaters]] | ||
:[[Stability of rubble mound breakwaters and shore revetments]] | :[[Stability of rubble mound breakwaters and shore revetments]] | ||
Revision as of 14:20, 20 May 2020
Contents
Introduction
An artificial reef (AR) can be defined as any solid man-made structure which has been submerged in the natural environment (Bohnsack, 1989[1]). Artificial reefs are often also called low-crested structures (LCS). They may be purposely placed to alter local hydrodynamics (coastal defense ARs) or this effect may be incidental (ship wrecks, offshore windmills, oil rigs etc.). Regardless of their construction or purpose, artificial reefs generally involve the introduction of a hard substrate to a soft bottom environment, altering both the abiotic as the biotic properties of the environment. Coastal defense artificial reefs are therefore often constructed as multipurpose structures, i.e. besides the main function to defend the coast from erosion they also maximise secondary objectives such as to improve spot surfability, to stabilize nourishment material and to create marine parks of increased biodiversity. Since different aims, materials and configurations as well as site dependent factors are to be considered, design criteria for these structures are not easily defined a priori.
Materials
Stones
Stones are especially used for rubble mound structures whose hydraulic stability is verified through the formulae available in literature for low-crested structures (Burcharth et al., 2007 [2]). Un-corrected design of the structure by a wrong selection of stone size causes a low efficiency of the AR. Structure reshaping induced by wave breaking over the reef may occur and produce instability, with stones rolling down from the structure. Stones are relatively cheaper than other materials but can be more dangerous for surfing safety. For more detailed information, see Stability of rubble mound breakwaters and shore revetments.
Geobags, geotextile sand containers and geotubes
Geotubes consist of sacks made by geotextile that are filled with sand or gravel. They are characterized by a length and diameter of 20 and 3 m respectively and are particularly recommended for deep bottoms (Matteotti et al., 2003[3]). Geotextile sand containers (GSCs) and geobags are very similar to geotubes, although their dimensions are smaller than that and thus are usually adopted at lower depths. The cost of a reef made of GSCs is usually greater than in case of other materials because of the difficult placement. GSCs and geobags are often employed as revetments or as seaward slopes of nearshore structures. Unfortunately, no exhaustive analyses regarding element stability are available the need to combine numerical and physical models with practice and experience in the field to establish the real stability of the GSC remains. For more detailed information, see Sand-filled geosystems in coastal engineering.
The Narrowneck reef (figure 1) is perhaps the most successful example of an Artificial Surfing Reef (ASR) because it requires a modest maintenance degree, while a lot of benefits are obtained in terms of coastal defense and development of surfing sports. The required maintenance after the construction has been very low, consisting in the addition of only 50 GSCs in 6 years (Jackson et al, 2007[4]). The main objectives of this ASR were to enlarge the beach and to improve the spot surfability. Therefore, this reef consists of two arms with a central channel in between to ensure slow rip currents (Jackson et al, 2002[5]). The ASR in Narrowneck is composed of 458 geotubes, placed at depths ranging between 1.5 (crest) to 10 meters water depth (low tide). The reef is 270 m long (cross shore direction) and 170 m wide (longshore direction), covering a total volume of 120,000 m3. The geotextile sand containers were filled with 100-300m3 of native sand in order to eliminate the contamination hazard in case of breaking (Jackson et al, 2002[5]). The Narrowneck reef contributes significantly to the stabilisation of the nourished beach and induced the formation of a salient which is approximately 50 m wide cross-shore. With regards to the second goal, surfable waves are reproduced on average for 184 days/year, with spilling or plunging breakers in case of weak storms and typically plunging breakers for intense storms (Jackson et al, 2007[4]). Finally, the GSC surface was found to be intensely colonized by marine flora (Jackson et al, 2007[4]).
Reef units
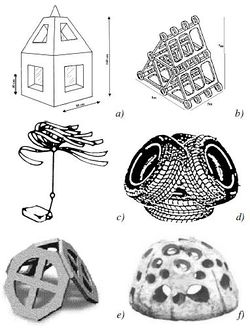
Reef units of different shapes and constructive characteristics can be used to produce ARs. Their macro-roughness reduces the incident wave agitation above the reef, creating local turbulence and vortices. Usually they are made by steel, reinforced or pre-stressed concrete, fibreglass or a variety of composite materials. These units are produced individually on shore and transported to the staging area. Here they could be combined in a variety of configurations thus allowing adjustment to local conditions and needs. Most of the units are designed to provide nursery areas for fish, to permit a good water recirculation, promote current deflections and marine colonization (O’Leary, 2001[6]). Some examples are shown in figure 2.
Figure 2e shows the so-called tecnoreef modules. Constructed from concrete-based natural products, they pose little impact on the ecosystem. Each module consists of reinforced octagonal plates, which are characterized by holes (usually four) having a quarter of a circle shape. The modules are assembled together to create a sort of pyramid that usually consists of three octagonal plates, the so called “base system”. The structure basis is made larger than the crest thus ensuring the resistance and stability to cross-shore currents and drag forces. They globally reduce cross-shore currents due to friction and turbulence. The consequent deposition of transported sediments within and around the pyramids is increased by the differently inclined facets on the external and internal surfaces of the modules. These irregularities facilitate localized microcurrents and create continuous circular currents (spheres of water) which release their energy upwards within each element. The constant circulation and exchange of water allows the influx of nutrients and permanent occupation by flora and fauna.
Equally note-worthy are the reef ball elements shown in figure 2f. These have an hemispherical shape (Harris, 1995[7]) and are typically 1-2 m high and 2 m wide. A reef ball is made by polyester with glass reinforcement and is thus very resistant to corrosion. The reef ball contains a buoy that allows it to float during construction phase and that is deflated when the element is definitively placed. They are characterised by high porosity (40-50%), roughness and many cavities or holes which have a double action. First off, the roughness and holes increase the structure complexity which assures a quick colonisations by marine species and aquatic plants (Pilarczyk, 2003[8]). Secondly, these structures are specifically designed to generate turbulence, vortices and vertical jets which dissipate wave energy. Under storm attacks, the geometry of reef balls reduces the stability whereas the porosity, through the reduction of lifting forces, causes a beneficial compensating effect.
The Grand Cayman reef (Cayman Islands) was one of the first examples of a Reef ball artificial reef. Between 2002 and 2005, approximately 230 Reef Ball units, ranging in size between 9 to 11 m width and 1.3 to 1.6 m height, were placed in 5 rows on the predominantly rocky bottom (Harris, 2009[9]). A gap is placed in front of the shallowest and widest part of the adjacent natural rock reef. The purpose of the reef was to restore the beach in front of the “Marriott beach resort” that disappeared in 2002 due to severe erosion during storm surges. The monitoring activities during the years 2002-2007 (Arnouil, 2008[10]) documented an average shoreline accretion of 18 m just 3 months after the reef installation and an almost complete beach restoration (peak width of 30 m) in 2006. The profile of the beach showed some relevant changes. In 2002, before the construction of the reef, the elevation of the highest point was below mean sea level. After the reef construction there was a significant increase in elevation, from +1.0 m to +1.8 m along the shore (3 months later). Between 2003 and 2007 a berm formation was observed in correspondence of the reef. The berm height (from +0.7 m to +1.0 m) and width (from 7 m to 10 m) are increased significantly till the summer of 2007 and then appeared stable same till now (Arnouil, 2008[10]).
Geometry
Layout
There are many schemes adopted for ARs, especially for those made by geotextile, depending on their principal function. After defining the objectives to be achieved, an appropriate geometry can be selected. Here, the case of submerged structures that are used to defend the coast from erosion are primarily considered. The layout in figure 3a represents the traditional configuration of gap separated rubble mound barriers parallel to the littoral zone. The waves that break over the reef induce an inshore increase of sea level and a simultaneous decrease of wave height due to energy dissipation over the crest (Pilarczyk, 2003[8]). Figure 3b - 3f shows some sample layouts for artificial reefs and artificial surfing reefs (ASRs). Overall, the structure is composed by two convergent wedges and a focus where the waves break (Ranasinghe et al., 2006[11]), defining a-frame waves, i.e waves that break in a central point while the breakpoint evolves in a symmetrical way from the case of submerged structures that are used to defend the coast from erosion. The geometries in figures 3d and 3f show a large front of the structure parallel to the shore and thus are characterized by an intermediate behaviour between a simple AR and an ASR. Many modifications exist where a central channel (also referred to as a rip channel or paddling channel) is introduced to the scheme (Van Ettinger, 2005[12]). Fig. 3f represents such an ASR with a central gap. The focus gap can be at the same depth of the seabed or raised from it. The rip channel reduces the intensity of rip currents and thus increase safety of surfers.
Cross-section
The cross-section of ARs varies according to the used materials and the main function of the structure. Figure 4a shows the cross section of a submerged barrier made of GSCs. The crest width of such a reef is much greater than that of traditional low crested structures and rubble mound breakwaters. The crest width must in fact be sufficiently large to dissipate wave energy (Pilarczyk, 2003[8]). Moreover, both seaward and landward slopes are steeper than in traditional breakwaters, reducing the volumes of material together with construction costs. In the body of the barrier, GSCs are longitudinally disposed whereas on the landward and seaward slopes GSCs are transversely disposed (Koerner et al., 2006[13]). This reduces the number of gaps which are exposed to breaking waves, increasing AR stability (Recio et al., 2009[14]). In figure 4b, the body of the reef is composed by differently sized GSCs in order to fill all the gaps between the GSCs (Recio et al., 2009[14]), while the seaward and landward slopes are covered by geotubes. Clearly, for geotubes stability the angle at seabed must be lower than in the previous scheme. Figure 4c shows an Aquareef that is composed by an internal core made of rubble stones and one upper layer of special blocks that induce localized turbulence, dissipating incident wave energy. This scheme is the most common on Japanese coasts (Pilarczyk, 2003[8]). The Iburi reef in Hokkaido is an example of this peculiar reef design. In figure 4d the core of the reef is made of geotubes characterized by different dimensions while armour and filter layers are composed by stones (Pilarczyk, 2003[15]). This ASR profile is characterized by a submerged crest over which the waves peel (figure 4). A linear or convex profile for wedges can be adopted (Van Ettinger, 2005[12]). A convex profile can better compensate the change of the breaker intensity but it is more difficult to be constructed while the easier constructed linear profile creates the phenomenon of “wave pinching” i.e. a reduction of the pipe under plunging waves (Mead, 2003[16]). At the back of the ASR, wedges can be cut or uncut to modulate the velocity of rip and longshore currents. If a cut profile for wedges is adopted, the velocity of rip currents is generally lower than with the un-cut profile (Van Ettinger, 2005 [12]).
Dimensions
The size of the barrier depends on its use. If we consider a barrier for coastal protection, as in figure 3a, the parameters to be estimated are the crest and gap width (Pilarczyk, 2003[8]). For the first it is important to define the desired transmitted wave height or, in other words, the transmission coefficient. For the second, it is important to estimate the rip current velocities in order to establish an appropriate gap width. Moreover, it has to be considered that an increase of the rip channel may decrease the speed of rip currents but, at the same time, it may increase the transmission coefficient [math]K_T[/math] (Van der Meer et al., 2005[17]). Another critical parameter is crest submergence, since it has to cope with the desired value of [math]K_T[/math] as well as account for safe conditions for swimmers and surfers within the tidal excursion of the construction site. The depth of the structure crest has to be related to the breaking wave height. The following method (USACE, 2012[18]) is provided for estimating the wave breaking height ([math]H_b[/math]) and breaking depth ([math]h_b[/math]). This method is based on the deep water un-refracted wave height ([math]H'_b[/math]), the offshore wave length ([math]L_0[/math]) and the seabed slope ([math]m[/math]).
By defining the breaker height index as: [math]\omega_b= 0.56\left (\large\frac{H_0\prime}{L_0} \normalsize\right)^{-0.2}[/math]
the wave breaking height is: [math]H_b=H_0 \cdot \omega_b[/math].
Deriving [math]H_b[/math] from this equation, provided the breaker index [math]\omega_b[/math] is known and the waves are depth-limited, it can be written: [math]h_b= \left ( \large\frac{H_b}{\gamma_b} \normalsize \right )[/math].
[math]H_b[/math]H can be estimated by the following formula: [math]\gamma_b=b-a \left ( \large\frac{H_b}{gT^2} \normalsize \right )[/math],
where [math]a[/math] and [math]b[/math] depend on the seabed slope [math]m[/math] as follows: [math]a=43.8 \cdot(1-e^{-19m}) , \quad b=\left (\large\frac{1.56}{1+e^{-19.5m}} \normalsize \right )[/math].
The appropriate crest width of the reef ([math]B[/math]) can be derived considering:
- the reef crest must be greater than the plunge distance which is the distance between plunge and break point, in order to assure that waves break over the crest. There is an empirical formula based on laboratory tests (Smith and Kraus, 1990[19]) that provide the plunging distance [math]X_P[/math].
- [math]B[/math] is related to the transmission coefficient KT (Pilarczyk, 2003.a[8]) and therefore, fixing an appropriate value for [math]K_T[/math], [math]B[/math] is derivable from some formulae in literature: [math]X_p=H_b \cdot (0.63\xi^{-1}+1.81)[/math], where the Iribarren and Battjes parameter [math]\xi=\large\frac{m}{\sqrt(H/L)} \normalsize [/math] must satisfy the condition [math] \; 0.29 \lt \xi \lt 3.46 [/math].
The wave transmission coefficient [math]K_T[/math] is typically in the range 0.3-0.7 for a cross-section of an Aquareef. Transmitted wave heights decrease with increasing relative wavelength and are affected by wave breaking. If [math]3R_c / H_i[/math] is relatively small, with [math]R_c[/math]= the submergence (freeboard), [math]H_i[/math]= the incident wave height, waves easily break on the reef and in this particular case [math]K_T[/math] is smaller than in the other cases (Hirose et al., 2002[20]). It is observed that wave energy dissipation (Hamaguchi et al., 1992[21]) is greater for the Aquareef unit type than for the rubble stones, though the values are similar when [math]R_c / H_i \lt 1[/math]. Therefore [math]K_T[/math] can be determined by formulae valid for submerged rubble mound structures (Van der Meer et al., 2005 [17]), which include the crest width [math]B[/math] to describe the behavior of [math]K_T[/math] when [math]R_c=0[/math]. For example, the d’Angremond et al. formula (1996[22]) reads:
[math]K_T=-0.4 \left(\large\frac{R_c}{H_i} \normalsize \right)+0.64 \left(\large\frac{B}{H_i} \normalsize \right)^{-0.31}\cdot(1-e^{-0.5\xi})[/math].
In this formula, [math]K_T[/math] is limited between 0.075 and 0.8. This equation tends to overestimate [math]K_T[/math] when [math]B/H_i \gt 10[/math] and therefore an attempt to improve the description of [math]K_T[/math] was done in recent studies (Van der Meer et al., 2005[17]). A suitable formula (Van der Meer et al., 2005[17]) for submerged structure having a large relative crest width is:
[math]K_T=-0.35\left(\large\frac{R_c}{H_i} \normalsize \right)+0.51 \left(\large\frac{B}{H_i} \normalsize \right)^{-0.65}\cdot(1-e^{-0.41\xi})[/math].
Artificial Surfing Reefs (ASR)
For artificial surfing reefs, the dimensions of the arms strongly depend on the extension of the surf area and on the desired breakpoint length. The design elements to define are the crest submergence, wedge slopes, rip-channel width and aperture angle [math]\delta[/math]. Crest submergence can be designed based on the criteria already provided. The main goals of the ASR wedges are to create surfable breakers (Ranasinghe et al., 2006[23]), according to the required surf category (bodysurfing, bodyboard, paddle board, short board, etc.). Therefore the wedge slopes m must be determined basing on appropriate values of the Iribaren/Battjes parameter [math]\xi[/math] (Battjes, 1974[24]). Surfable breakers are characterized by [math]0 \lt \xi \lt 0.5 [/math] for spilling and [math]0.5 \lt \xi \lt 3.3[/math] for plunging breakers, but is also preferable to have values between 2.0 and 3, which clearly characterize plunging breakers (Scarfe, 2002[25]). Moreover, in the plunging category, it is possible to distinguish the type of breaker based on the vortex ratio defined as follows (Mead and Black, 2000[26]): [math]VR=\large\frac{F}{W} \normalsize [/math] with [math]F[/math] and [math]W[/math] being the tube dimensions subtended by the plunging breaker. [math]VR[/math] also depends on seabed slope [math]m[/math] and particularly it increases as [math]m[/math] decreases. Plunging breakers are characterized by low values of [math]VR[/math] (typically between 1.6-2.5), while higher values of [math]VR[/math] characterize less intense breaking. Generally, vortex ratio depends on slope [math]m[/math] as follows (Mead and Black, 2000[26]) [math]VR=0.065 \cdot m^{-1}+0.821[/math].
Finally, the rip channel elements must be fixed in order to reduce the speed of central and lateral rip currents. Unfortunately, no formulae have been developed so far that synthetically provide [math]b[/math] and [math]\delta[/math]; but some examples of numerical models exist in literature (Van Ettinger, 2005[12]; Muilwijk, 2005 [27]; Trung, 2006[28]) which show that by increasing of angle [math]\delta[/math], the rip current through the channel decreases (Van Ettinger, 2005[12]).
Function
ARs dissipate incident waves by breaking and thereby reduce inshore wave agitation and increase the tendency to create geomorphologic forms (Pilarczyk, 2003[8]), i.e salient or tombolo, which vary accordingly to AR dimensions and to sediment size. The rules for low-crested structures (LCSs) and ARs are recalled below (Pilarczyk, 1996[29]):
[math]\large\frac{L_S}{X} \normalsize \gt 0.66 (1-K_T)[/math] (tombolo), [math]\quad \large\frac{L_S}{X} \normalsize \gt \large\frac{1}{(1-K_T)}[/math] (salient and single reef), [math]\quad \large\frac{G L_S^2}{X} \normalsize \gt 0.5 (1-K_T)[/math] (salient and multi-reef),
where [math]L_S[/math] is the longshore dimension of the reef and [math]X[/math] the offshore distance. The gap width is usually [math]L \le G \le 0.8 L_S[/math], where [math]L[/math] is the wave length. Field data along Australian coasts indicate that tombolo and salient formation (Black and Andrews, 2001[30]) occurs when:
[math]\large\frac{L_S}{X} \normalsize \gt 0.6[/math] (tombolo), [math]\quad \large\frac{L_S}{X} \normalsize \lt 2[/math] (salient).
Furthermore, the distance between the tip of the salient and the offshore reef ([math]X_{off}[/math]) can be predicted from the longshore dimension of the offshore reef ([math]L_S[/math]) by the following formula (Andrew, 1997[31]): [math]\large\frac{X_{off}}{L_S} \normalsize =0.5 \left(\large\frac{L_S}{X} \normalsize \right)^{-1.27}[/math].
Ming and Chiew (2000[32]) showed that salient occurs behind a detached breakwater when [math]\large\frac{X}{L_S} \normalsize \gt 0.8[/math] and determined the plan area of sand deposition ([math]A[/math]) as the area enclosed by the initial shoreline and the shoreward equilibrium shoreline: [math]\large\frac{A}{X^2} \normalsize =-0348+0.043\large\frac{X}{L_S} \normalsize +0.711\large\frac{L_S}{X} \normalsize [/math].
Problems resulting from the increasing submergence [math]R_c[/math] are different for ARs or for ASRs as they are mainly related to their specific purposes (Pilarczyk, 2003.a[8]). For an AR, [math]R_c[/math] directly affects the transmission coefficient [math]K_T[/math] and hence a higher residual wave agitation behind the reef will be observed. Therefore, the AR tends to be less effective for coastal defence and the most common way to restore the initial value of [math]R_c[/math] is to perform a rock/element recharge on the structure crest. For an ASR, the problem is the increase of [math]K_T[/math] and a decrease of spot surfability, due to an increase of breaking wave heights based on depth limited conditions (Van Ettinger, 2005[12]). This means that a greater surfer ability is required to ride the waves (Mead, 2003), and this may decrease the number of persons for which the ASR was originally conceived. Additionally, the number of surfable days per year may decrease (Mead, 2000a), since higher incident waves are needed to maintain the same hydrodynamic conditions over the reef. Also in this case, the most common way to cope with sea level rise and changes of [math]R_c[/math] is to place one or more additional layers of material over the ASR crest.
See also
- Natural shore protecting barriers
- Detached breakwaters
- Stability of rubble mound breakwaters and shore revetments
- Sand-filled geosystems in coastal engineering
- Theseus Official Deliverable 2.1 - Integrated inventory of data and prototype experience on coastal defences and technologies
- The Rock Manual (2007)[33]
- The Coastal Engineering Manual (2012)[18]
- The Eurotop Manual (2018)[34]
Appendix: Design of Artificial Reefs made of Geotextile Sand Containers
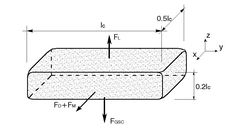
Specific analysis of structure stability under non breaking waves exists in the literature for ARs made by GSCs or geobags (Recio et al, 2009[14]) or reef units (Harris, 2009[9]). In case of structures made by stones, design methods refer essentially to the studies available for LCSs (Burcharth et al., 2007[35]). Few studies exist dealing with deeply submerged structures that may act as a local increase of bottom roughness that dissipates energy depending on local wave length (Corvaro et al., in press[36]). The force system acting on a single GSC is summarised in figure 5. In this scheme, the container is assumed to be a rigid body and is characterised by a width that is half of the length [math]l_c[/math] and a height is 0.2 times the length.
The forces acting on GSC are (Recio et al, 2009[14]
Drag force [math]F_D=0.5 C_d \cdot \rho_w \cdot A_s \cdot u^2 ; \quad[/math] Inertia force [math]F_i=C_m \cdot \rho_w \cdot V \cdot \partial u / \partial t ; \quad[/math] Lift force [math]F_L=0.5 \cdot C_L \cdot \rho_w \cdot A_T \cdot u^2 ; \quad[/math]
Buoyancy force [math]F_B=g \cdot \rho_w \cdot V ; \quad [/math] Weight force [math]F_{GSC}=g \cdot \rho_s \cdot V \quad[/math],
where [math]A_t=l_c^2/2, \quad A_s=l_c^2/10, \quad V=l_c^3/10[/math], and where [math]C_d, C_m, C_L[/math] are drag, inertia and lift coefficients, respectively. These can be estimated based on experimental results (Recio, 2008[37]). The sliding and overturning equilibrium conditions are, respectively (Recio et al, 2009[14]),
[math]\mu (F_{GSC}-F_L) \ge F_D + F_M , \quad F_{GSC} l_c/2 \ge F_M l_c /10 + F_D l_c /10 + F_L l_c /2 , [/math]
where [math]\mu[/math] is the dimensionless friction factor and [math]u[/math] the orbital velocity. A key issue for the proper design of ARs made with GSC is to account for the effect of the GSC deformation. GSC deformability can be taken into account (Recio et al, 2009 [14]) by 1) introducing new deformation factors for the mobilizing forces ([math]K_{CD}, K_{CL}, K_{CM}[/math]) dependent of the sand fill ratio of GSC, wave conditions, properties of the filling material and deformation of the geotextile; 2) by introducing new deformation factors for the resisting forces ([math]K_R[/math]) which depend on sand fill ratio of GSC, properties of the filling material, wave conditions, steepness of the structure slopes and position and number of adjacent GSCs; 3) by modifying the existing force coefficients ([math]CD, CM, CL[/math]). However, [math]CD[/math] and [math]CL[/math] are a function of the Reynolds number [math]Re[/math] and of the roughness and thus they are influenced also by the wave-induced flow around the GSC and by its shape.
Physical model tests (Recio, 2008) [37] are the only way to derive the corresponding coefficients modified by deformations effects ([math]CD', CM', CL'[/math]). Approximation for the values of these coefficients can be found in Recio and Oumeraci (2009) [14]. Expressions to estimate the new coefficients to be introduced are first synthesised in case sliding equilibrium is considered. Regarding the resisting force [math]F_{GSC}[/math], the GSC deformations affects the projected weight forces of the GSC and thus also modifies its stability (Recio et al., 2009). Generally, [math]K_R[/math] varies accordingly to the part of the structure that is considered, particularly the slope or the crest. In order to estimate sliding deformation factors ([math]KS_{CD}, KS_{CL}, KS_{CM}[/math]) the condition for sliding equilibrium, Eq. (30), is applied. [math]KS_{CD}[/math] can be evaluated only by the variation of the projected area [math]A'_S=0.14 \, l_c^2[/math] normal to the wave direction (Recio et al., 2009[14]) as follows: [math]KS_{CD}=A'_S / A_S=1.4[/math].
Since the volume of the container remains constant (thus the influence of shape variation on the added mass is small) and inertia forces are smaller than drag forces, especially in shallow water, [math]KS_{CM}[/math] can be assumed equal to 1,0 (Recio et al., 2009[14]). [math]KS_{CL}[/math] is influenced by the variation of the projected area in the wave direction ([math]A'_T = 0.47 \, l_c^2[/math]) and thus results: [math]KS_{CL}=A'_T / A_T =0.94[/math]. Finally, the deformation factor for the resisting force is defined as [math]KS_R=V'/ V[/math], where [math]V'=0.16 \, l_c^3[/math] and [math]V = 0.1 \, l_c^3[/math], giving [math]KS_{R}=\large\frac{V\prime}{V}\normalsize =1.60[/math]. However, [math]KS_R[/math] depends also on the seabed slope angle [math]\alpha[/math] (Recio et al., 2009 [14]): [math]KS_R=0.0007 \cdot \alpha^2 +0.25 \cdot \alpha-6.83[/math]. Since similar deformations occur for containers placed on the slope and on the crest, it is reasonable to assume that the deformation factors are the same with the exception of [math]KS_R[/math]. In fact shape variations are greater for GSCs placed on the seaward slope than on the crest (Recio, 2008[37]). For GSC on the crest, [math]KS_R[/math] becomes (Recio et al., 2009 [14]): [math]KS_{R}=\large\frac{V\prime}{V}\normalsize =0.70[/math] and depends on the slope angle: [math]KS_R=-0.00009 \cdot \alpha^2 +0.019 \cdot \alpha-0.008[/math].
Expressions to estimate the new coefficients to be introduced are now synthesised in case overturning equilibrium is considered. For the overturning equilibrium the deformation factors [math]KO_{CD}, KO_{CM}, KO_{CL}, KO_{R}[/math] account, in this case, for the variation both of forces and moments (Recio et al., 2009[14]). For the moment due to the drag force, the factor [math]KO_{CD}[/math] should be estimated as: [math]KO_{CD}=\large\frac{A\prime_S}{A_S}\normalsize \cdot \large\frac{z\prime_{CD}}{z_{CD}}\normalsize \cong1.54[/math]. Similarly, deformation factors related to Morison (inertia) and lift forces are respectively: [math]KO_{CM}=\large\frac{z\prime_{CM}}{z_{CM}}\normalsize \cong1.1, \quad KO_{CL}=\large\frac{A\prime_t}{A_t}\normalsize \cdot \large\frac{x\prime_{CL}}{x_{CL}}\normalsize \cong0.80[/math], where [math]z[/math] is moment arm on the [math]z[/math]-axis. Finally, assuming that the GSC volume in deformed configuration is the same as in the non-deformed configuration, [math]KO_R[/math] results: [math]KO_{R}=\large\frac{x\prime_{GSC}}{x_{GSC}}\normalsize \cong0.92[/math], with [math]x[/math] being the moment arm on the [math]x[/math]-axis.
To apply the hydraulic stability formulae, the required parameters are:
- the wave-induced horizontal velocity u at the depth of the critical GSC. This velocity can be derived from simple analytical models based on linear wave theories.
- the wave-induced horizontal acceleration at same depth [math]\partial u / \partial t[/math];
- the friction factor [math]\mu[/math] between GSCs, which can be derived from physical model tests;
- the force and deformation coefficients.
However, in the design phase it is too difficult to define [math]C_D, C_M, C_L[/math] because they are functions of the Reynolds number, that also depends on the unknown size of the container. The following iterative procedure is proposed (Recio et al., 2009[14]):
- by using linear wave theory, the wave-induced orbital velocity [math]u[/math] and acceleration [math]\partial u / \partial t[/math] at the depth of the critical container can be calculated;
- the Reynvolds number [math]Re[/math] is computed and consequently the coefficients [math]C'_D, C'_M, C'_L[/math] and the deformation factors [math]K_{CD}, K_{CM}, K_{CL}, K_{R}[/math] can be selected from the corresponding range (Recio, 2009[14]);
- the GSC length [math]l_{GSC}[/math] is derived as the length that satisfies the equilibrium conditions for sliding and overturning;
- based on the obtained value for [math]l_{GSC}[/math]l value, calculate again Reynolds number [math]Re[/math], [math]C'_D, C'_M, C'_L, K_{CD}, K_{CM}, K_{CL}, K_{R}[/math], and then re-calculate the required length [math]l_c[/math].
It is recommended to use the maximum velocity [math]u[/math] together with the maximum acceleration [math]\partial u / \partial t[/math] (Recio et al., 2009[14]), although their phases are shifted by [math]\pi / 2[/math] and theoretically, when occurs the maximal drag force (influenced by [math]u^2[/math]), the inertia force [math]F_M[/math] (influenced by [math]\partial u / \partial t[/math]) tends to zero.
Under breaking waves, the GSC behaves as flexible body, being uplifted and deformed by wave impact. Breaking wave loads cause very high overpressures on GSC surfaces in very short time intervals and therefore the elements are exposed to static and impulsive loads. In these conditions, it may happen that high pressures, especially at sea water level, tend to separate adjacent GSCs, generating a flow in between and a resulting increase of the pressures acting on the seaward slope of around two times, due to the superposition of incoming and reflected waves from the gaps. This process could lead to a seaward displacement of GSCs and thus be critical for structure stability.
Currently, not many studies have investigated the stability of reef units under regular wave attacks. This is due to their different shapes and geometries that make it difficult to elaborate a generalized theory. In this section only the reef balls are considered. Other reef elements are characterized by different geometries and shapes, which generally cannot be compared to that of Reef Balls and hence require specific knowledge beyond the following. The stability criterion is derived by applying the sliding equilibrium (Harris et al., 1998[38]), where the horizontal wave force acting on the reef unit can be decomposed into drag and inertia forces and the resisting force is due only to the friction between the element and the seabed (Harris et al., 1998[38]). Therefore. in order to estimate the right dry weight that ensures the stability, the sliding equilibrium can be rewritten as (Harris et al., 1998[38]):
[math]F_{W}\ge\large\frac{F_S}{\mu}\normalsize (F_D+F_i)+F_l+F_B ,[/math]
where [math]F_D, F_i, F_B, F_L[/math] can be estimated through the given equations above and [math]F_W[/math] is the dry weight of the unit. The friction factor [math]\mu[/math] can be assumed equal to 0.4 for sliding on sand bottom or 0.5 on hard bottom (Harris et al., 1998[38]) and [math]F_S[/math] is a safety factor. The forces are very difficult to estimate and thus several laboratory tests were carried out under regular waves in a wave tank (Harris et al., 1998[38]). These tests provided for selected wave conditions a relationship between the unit weight and the water depth, which strongly affects the horizontal water particle velocity and acceleration and hence the drag and inertia forces. The initial relationship between depth and dry weight being almost linear, there is a peak that represents a critical depth value beyond which the minimum dry weight (and therefore, the stability) is not affected by the depth (i.e. the curves tend to become horizontal)(Harris et al., 1998[38]).
References
- ↑ Bohnsack, J.A., 1989. Are high densities of fishes at artificial reefs the result of habitat limitation or behavioral preference? Bulletin of Marine Science. 44, 631-645.
- ↑ Burcharth, H. F., Hawkins, S., Zanuttigh, B., and Lamberti, A., 2007. Environmental Design Guidelines for Low Crested Coastal Defence Structures, Elsevier.
- ↑ Matteotti G., Ruol P., 2003. L’impiego dei geosintetici nelle opere di ingegneria marittima e costiera, 2003 [1]
- ↑ 4.0 4.1 4.2 Jackson, L, Corbett, B., Tomlinson, R., McGrath, J., Stuart, G., 2007. Narrowneck Reef: Review of Seven Years of Monitoring. [2]
- ↑ 5.0 5.1 Jackson, L.A., Tomlinson R., McGrath, J., Turner, I., 2002. Monitoring of a multi functional submerged geotextile reef breakwater. Proceedings of the 28th International Conference on Coastal Engineering 7-12th July 2002 Cardiff, Wales.
- ↑ O’Leary, Hubbard T., O’Leary D. Artificial Reefs Feasibility Study, Coastal Resources Centre National University of Ireland Cork, 2001
- ↑ Harris, L.E., 1995. Engineering design of artificial reefs. Oceans '95, Marine Technology Society, Washington, D.C., Vol. 2, pp. 1139-1148.
- ↑ 8.0 8.1 8.2 8.3 8.4 8.5 8.6 8.7 Pilarczyk, K.W., 2003. Alternative systems for coastal protection: an overview. International Conference on Estuaries and Coasts November 9-11, 2003, Hangzhou, China.
- ↑ 9.0 9.1 Harris, L.E., 2009. Artificial Reefs for Ecosystem Restoration and Coastal Erosion. Protection with Aquaculture and Recreational Amenities, Reef Journal. 1(1), pages 235-246.
- ↑ 10.0 10.1 Arnouil D.S., 2008. Shoreline Response for a Reef Ball Submerged Breakwater System Offshore of Grand Cayman Island. Thesis of Master of Science in Ocean Engineering, submitted to Florida Institute of Technology, Florida (2008). [3]
- ↑ Ranasinghe, R., Turner, I.L., 2006. Shoreline response to submerged structures: A review. Coastal Engineering. 53, 65– 79.
- ↑ 12.0 12.1 12.2 12.3 12.4 12.5 Van Ettinger, H.D., 2005. Artificial surf reef design. Thesis at Delft University of Technology, 2005. [4]
- ↑ Koerner, G.R., Koerner, R.M., 2006. Geotextile tube assessment using a hanging bag test. Geotextiles and Geomembranes. 24, 129–137
- ↑ 14.00 14.01 14.02 14.03 14.04 14.05 14.06 14.07 14.08 14.09 14.10 14.11 14.12 14.13 14.14 Recio, J., Oumeraci, H., 2009. Process based stability formulae for coastal structures made of geotextile sand containers. Coastal Engineering. 56, 632–658.
- ↑ Pilarczyk, K.W., 2003. Design of low-crested (submerged) structures – an overview. 6th International Conference on Coastal and Port Engineering in Developing Countries, Colombo, Sri Lanka.
- ↑ Mead, S., 2003. Surfing Science. Proceedings of the 3rd International Surfing Reef Symposium, Raglan, New Zealand, June 22-25, 2003.
- ↑ 17.0 17.1 17.2 17.3 Van der Meer, J. W., Briganti, R., Zanuttigh, B.,Wang, B., 2005. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coastal Engineering. 52, 915–929.
- ↑ 18.0 18.1 USACE, 2012. Coastal engineering manual. Report No 110-2-1100. Washington DC: US Army Corps of Engineers https://www.publications.usace.army.mil/USACE-Publications/Engineer-Manuals/u43544q/636F617374616C20656E67696E656572696E67206D616E75616C/
- ↑ Smith, E. R., Kraus, N.C., 1991. Laboratory study of wave-breaking over bars and artificial reefs. Journal of Waterway, Port, Coastal and Ocean, 1991.
- ↑ Hirose, N., Watanuki, A., Saito, M., 2002. New Type Units for Artificial Reef Development of Eco-friendly Artificial Reefs and the Effectiveness Thereof. PIANC Congress, Sydney, see also 28th ICCE, Cardiff.
- ↑ Hamaguchi, N. Watanuki, A., Hasegawa, M., Noguchi, M., 1991. Development of submerged breakwaters for harmonized fisheries. Proceedings of The Japanese Society of Fisheries Engineering, 67-68.
- ↑ d’Angremond, K., van der Meer, J.W., de Jong, R.J., 1996. Wave Transmission at Low-Crested Structures. Coastal Engineering 1996, pp. 2418-2427.
- ↑ Ranasinghe R., Turner, I.L., 2006. Shoreline response to submerged structures: A review. Coastal Engineering. 53, p65– 79
- ↑ Battjes J. A., 1974. Surf Similarity. Proceedings 14th Coastal Engineering Conference, ASCE, pp: 466-480.
- ↑ Scarfe, B. E., 2002. Categorising Surfing Manoeuvres Using Wave and Reef Characteristics. Unpublished MSc Thesis, University of Waikato, Hamilton, New Zealand.
- ↑ 26.0 26.1 Mead, S. T., Black, K. P., 2000. Predicting the Breaking Intensity of Surfing Waves. Special Issue of the Journal of Coastal Research on Surfing, pp: 51-65.
- ↑ Muilwijk, M.P., 2005. Artificial Surf Reef on Maasvlakte 2, Msc.Thesis, Delft University of Technology, Faculty of Civil Engineering and Geosciences, Section of Hydraulic Engineering, june 2005.[5]
- ↑ Trung L.H., 2006. Interacting Artificial Surf Reefs, MSc Thesis, 2006 (downloadable from www.jcronline.org).
- ↑ Pilarczyk, K.W. and Zeidler, R.B., 1996. Offshore breakwaters and shore evolution control, A.A. Balkema, Rotterdam.
- ↑ Black, K. and Andrews, C.J., 2001. Sandy Shoreline Response to Offshore Obstacles, Part I: Salient and tombolo geometry and shape, Part II: Discussion of Formative Mechanisms. Journal of Coastal Research, Special Issue on Surfing.
- ↑ Andrews, C.J., 1997, Sandy shoreline response to submerged and emerged breakwaters, reefs or islands. Unpublished Thesis, University of Waikato, New Zealand
- ↑ Ming D., and Chiew, Y-M., 2000. Shoreline Changes behind Detached Breakwater. J.Waterway, Port, Coastal, and Ocean Engng. 126(2), March/April.
- ↑ CIRIA/CUR/CETMEF 2007. The Rock Manual. The use of rock in hydraulic engineering (2nd ed.). C683. London: CIRIA
- ↑ Van der Meer, J.W., Allsop, N.W.H., Bruce, T., De Rouck, J., Kortenhaus, A., Pullen, T., Schüttrumpf, H., Troch, P. and Zanuttigh, B. 2018. Manual on wave overtopping of sea defences and related structures, 2nd ed. http://www.overtopping-manual.com/
- ↑ Burcharth, H. F., Hawkins, S., Zanuttigh, B. and Lamberti, A., 2007. Environmental Design Guidelines for Low Crested Coastal Defence Structures Elsevier.
- ↑ Corvaro, S., Mancinelli, A., Brocchini, M., Seta, E., Lorenzoni, C., On the wave damping due to a permeable seabed. Coastal Engineering, In Press.
- ↑ 37.0 37.1 37.2 Recio J. 2008, Hydraulic Stability of Geotextile Sand Containers for Coastal Structures –Effect of Deformations and Stability Formulae – PhD Thesis, Leichtweiss Institute for Hydraulic Engineering and Water Resources.
- ↑ 38.0 38.1 38.2 38.3 38.4 38.5 Harris L.E., Gonzalez J.E.C., 1998. Stability analysis for the submerged Reef Ball breakwater. proposed for the Mayan Palace Resort, Quintana Roo, Mexico", (1998 [6]
Please note that others may also have edited the contents of this article.
|
Please note that others may also have edited the contents of this article. |