Difference between revisions of "Breaker index"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 17: | Line 17: | ||
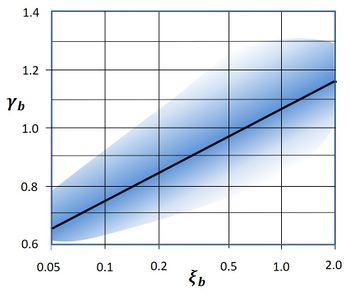
| − | [[File:BreakerIndex.jpg|thumb|left|350px|Fig. 1. The area covered by experimental data for the breaker index as a function of the surf similarity parameter. The density of the experimental data is represented by varying degrees of | + | [[File:BreakerIndex.jpg|thumb|left|350px|Fig. 1. The area covered by experimental data for the breaker index as a function of the surf similarity parameter. The density of the experimental data is represented by varying degrees of blueness. The black line is the Battjes formula Eq. 4. Figure adapted from Ostendorf and Madsen (1979<ref name=O>Ostendorf, D. and Madsen, O. 1979. An Analysis of Longshore Current and Associated Sediment Transport in the Surf Zone. Boston: Massachusetts Institute of Technology, Department of Civil Engineering Technical Report 241, 169p.</ref>).]] |
Experiments by Battjes (1974<ref name=B>Battjes, J.A. 1974. Surf similarity. Proceedings 14th International Conference on Coastal Engineering, pp. 466–480</ref>) suggested that this dependence on wavelength and bed slope could be represented by the [[surf similarity parameter]] | Experiments by Battjes (1974<ref name=B>Battjes, J.A. 1974. Surf similarity. Proceedings 14th International Conference on Coastal Engineering, pp. 466–480</ref>) suggested that this dependence on wavelength and bed slope could be represented by the [[surf similarity parameter]] | ||
Revision as of 23:08, 17 April 2021
Definition of Breaker index:
The ratio of wave height and still water depth at the shoreface location where waves start breaking.
This is the common definition for Breaker index, other definitions can be discussed in the article
|
Notes
The hydrodynamics in the surf zone and the associated sediment transport largely depend on the process of wave breaking. Waves break when the steepness of the wave front exceeds a certain limit. The wave breaking process is very complex. Hence, instead of solving the underlying dynamical equations, it is represented in most models by empirical formulas. These models therefore make use of the breaker index concept. This concept is based on observations showing that the wave height progressively decreases with depth in the surf zone. The strongest assumption is that the ratio of wave height and still water depth is constant throughout the surf zone,
[math]\large\frac{H(x)}{h(x)}\normalsize = \gamma = constant , \qquad (1)[/math]
where [math]H[/math] is the wave height, [math]h[/math] the still water depth and [math]\gamma[/math] the breaker index. This assumption is called saturated wave breaking.
This assumption is too rough for most applications. In a more refined approximation the two parameters wave steepness [math]H/L[/math] and the shoreface bedslope [math]m=\tan \beta[/math] are taken into consideration and the breaker index is evaluated at the breakpoint indicated by the subscript [math]b[/math],
[math]\large\frac{H_b}{h_b}\normalsize = \gamma_b . \qquad (2)[/math]
It may be expected that shorter waves will break earlier on the shoreface than longer waves (i.e. at greater depth for the same wave height), and that wave running over a steep slope will break later (i.e. at smaller depth) than waves running over a gentle slope. The breaker index should thus be an increasing function of the wavelength and the bed slope.
Experiments by Battjes (1974[2]) suggested that this dependence on wavelength and bed slope could be represented by the surf similarity parameter
[math]\xi=m / \sqrt{H/L} , \qquad (3)[/math]
according to the formula
[math]\gamma_b = 1.06 + 0.14 \ln \xi_b . \qquad (4)[/math]
Many other more elaborate formulas have been proposed. For example, the formulas by Ostendorf and Madsen (1979[1])
[math]\gamma_b = 0.14 \large\frac{L_b}{h_b} \normalsize \tanh(p \, k_b \, h_b) , \quad k=2 \pi / L , \; p = 0.8 + 5 \; min(m, 0.1) , \qquad (5)[/math]
and by Goda (2010[3])
[math]\gamma_b = 0.17 \large\frac{L}{h_b}\normalsize [1-exp(-\large\frac{3 \pi h_b}{L}\normalsize (1+11m^{4/3}))] , \qquad (6)[/math]
both requiring an iterative solution because of the dependence on [math]h_b[/math].
The results of experiments designed to determine the breaker index yield widely scattered results, even for experiments with similar bed slope and incident waves. Fig. 1 gives an impression of the range covered by experimental data when the breaker index is plotted as a function of the surf similarity parameter.
The formulas (4, 5, 6) were derived for regular monochromatic waves. Analysis of experiments [1][3] indicates that these formulas can also be applied for irregular waves with [math]H[/math] replaced by [math]H_s[/math] and with [math]\gamma[/math] multiplied by 0.7.
For gently sloping shorefaces, typically [math]m \lt 0.02[/math], it may be assumed that wave breaking is saturated throughout the surf zone, i.e. Eq. (1) approximately holds with [math]\gamma (x) = \gamma_b \; [/math][4]. For steeper slopes the ratio [math]H(x)/h(x)[/math] increases towards the shoreline[3].
Related articles
- Shoreface profile
- Shallow-water wave theory
- Surf similarity parameter
- Waves
- Wave set-up
- Littoral drift and shoreline modelling
References
- ↑ 1.0 1.1 1.2 Ostendorf, D. and Madsen, O. 1979. An Analysis of Longshore Current and Associated Sediment Transport in the Surf Zone. Boston: Massachusetts Institute of Technology, Department of Civil Engineering Technical Report 241, 169p.
- ↑ Battjes, J.A. 1974. Surf similarity. Proceedings 14th International Conference on Coastal Engineering, pp. 466–480
- ↑ 3.0 3.1 3.2 Goda, Y. 2010. Reanalysis of regular and random breaking wave statistics. Coastal Engineering Journal 52: 71-106
- ↑ LeMehaute, B . 1962. On non-saturated breakers and the wave run-up. Proceedings of the 8th International Conference Coastal Engineering, pp. 77-92, ASCE