Difference between revisions of "Coriolis acceleration"
Dronkers J (talk | contribs) |
Dronkers J (talk | contribs) |
||
| Line 57: | Line 57: | ||
|AuthorName=Dronkers J}} | |AuthorName=Dronkers J}} | ||
| − | [[Category: | + | [[Category:Physical coastal and marine processes]] |
| + | [[Category:Ocean and shelf sea]] | ||
[[Category:Hydrodynamics]] | [[Category:Hydrodynamics]] | ||
| − | |||
Revision as of 20:47, 28 June 2019
Definition of Coriolis acceleration:
Coriolis acceleration is the acceleration due to the rotation of the earth, experienced by particles (water parcels, for example) moving along the earth's surface. Ocean currents are influenced by Coriolis acceleration.
This is the common definition for Coriolis acceleration, other definitions can be discussed in the article
|
Coriolis acceleration is generated by the eastward rotation of the earth around the N-S axis.
This acceleration can be considered a purely kinematic effect by noting that time derivation in a rotating frame introduces a term related to rotation of the axes of reference [1]:
[math](d \vec r / dt)_{fixed frame} = \vec u + \vec \Omega \times \vec r ,[/math]
where [math]\vec r[/math] indicates the position of a fluid parcel on the rotating earth ([math]\vec r =0[/math] at the earth's centre), [math]\vec u \equiv d \vec r /dt[/math] is the velocity on the rotating earth, [math]\vec \Omega[/math] the rotation vector along the N-S rotation axis. The radial earth rotation frequency [math]\Omega \approx 7.3 \,10^{-5} s^{-1}[/math]. The acceleration then follows from
[math](d^2 \vec r /dt^2)_{fixed frame} = d \vec u /dt + \vec \Omega \times \vec u + \vec \Omega \times \vec u + \vec \Omega \times (\vec \Omega \times \vec r) .[/math]
The term [math]d \vec u /dt[/math] is the acceleration on the rotating earth, [math]2 \vec \Omega \times \vec u[/math] is the Coriolis acceleration and the term [math]\vec \Omega \times (\vec \Omega \times \vec r)[/math] is the component of the centrifugal force compensated by earth's attraction and adjustment of the equilibrium sea surface slope. If no forces are acting on the fluid and in the absence of friction, [math](d^2 \vec r /dt^2)_{fixed frame} =0 .[/math]
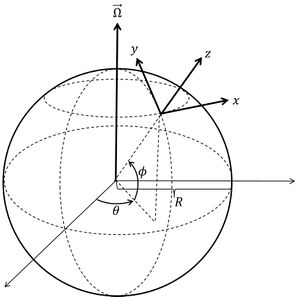
In order to find the more usual formulas for the Coriolis acceleration we use a system of axes on the rotating earth as indicated in figure 1, where [math]\theta[/math] is the azimuthal angle indicating longitude (expressed in radians), [math]\phi[/math] the elevation radian angle indicating latitude and [math]R[/math] is the earth radius. In this coordinate system the vector components are
[math]\vec u = (u=R \cos \phi \; d\theta / dt, v = R d \phi /dt, 0) , \; \vec \Omega = (0, \Omega \cos \phi, \Omega \sin \phi) .[/math]
The Coriolis acceleration is then given by:
[math]du/dt = f v, \; dv/dt = - fu, \; f=2 \Omega \sin \phi .[/math]
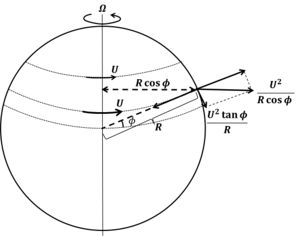
The Coriolis acceleration can be derived in a more intuitive way if we consider fluid velocities ([math]u,v[/math]) much smaller than the earth's surface rotation velocity [math]U = R \Omega \cos \phi[/math]. Due to the rotation of the earth, a centrifugal force, perpendicular to the earth's rotation axis, acts on ocean waters. This centrifugal force is only partly compensated by earth's attraction; it has a component acting along the surface of the earth towards the equator, see figure 2.
If water is at rest this tangential component of the centrifugal force is balanced by a sea surface slope. When seawater is brought into motion, this equilibrium is broken and water motion experiences Coriolis acceleration. A current [math]u[/math] in east-direction will experience an acceleration toward the equator as a result of the increased tangential component of the centrifugal force:
[math] dv/dt = - \sin \phi [(U+u)^2 - U^2]/R \cos\phi \approx - fu[/math] with [math]f = 2 \Omega \sin{\phi} . [/math]
The approximation is very accurate because in natural situations [math]|u| \lt \lt |U|[/math].
When fluid is travelling northward along the earth's surface with velocity [math]v = R d\phi/dt ,[/math] it experiences a decrease of surface rotation velocity [math]U[/math]. The principle of angular momentum conservation implies that the fluid will accelerate in order to conserve its angular momentum. This can be expressed as
[math]d[(U + u) R \cos \phi ] / dt = d[\Omega R^2 \cos^2 \phi + u R \cos \phi ] / dt =0 .[/math]
From this equation we find [math]du/dt = fv[/math], assuming again that [math]|u| \lt \lt |U| .[/math]
When fluid parcels are set in motion they thus experience an acceleration to the right on the northern hemisphere ([math]\phi\gt 0[/math]) and an acceleration to the left on the southern hemisphere. Because [math]f[/math] is small (typically on the order of [math]10^{-4}[/math]), earth's rotation hardly influences currents which fluctuate with higher frequencies, such as wave orbital motion. However, the influence on stationary currents or slowly varying currents, such as wind-driven flow and tidal motion, can be significant (see Coriolis and tidal motion in shelf seas). This is the case in wide basins, with width of the order or larger than [math]|\vec u + \vec v|/f .[/math]
A fluid moving freely (no external or frictional forces) in a wide basin (no water surface inclination), with initial velocity [math]V[/math], will describe a circular motion due to Coriolis acceleration:
[math]u=V \sin ft , \; v= V \cos ft .[/math]
The fluid follows an inertial circle with radius [math]V/f[/math]. This flow pattern can be sometimes observed when a strong river jet enters a wide basin.
Please note that others may also have edited the contents of this article.
|