Coriolis and tidal motion in shelf seas
Contents
Introduction
Tidal waves in wide basins are strongly influenced by earth's rotation (Coriolis acceleration). Tidal waves turn around so-called amphidromic points, where the vertical motion is almost nil. At some distance from the basin boundaries the tidal current vector describes an ellipse during the tidal period.
Assumptions
We will restrict the discussion to situations where the following assumptions approximately hold:
- a homogeneous shelf sea of uniform depth;
- a single (semi-diurnal) tidal component with radial frequency [math]\omega[/math] ;
- tidal motion driven by the ocean tide at the shelf boundary;
- tide-generating forces of moon and sun are negligible for the selected domain;
- latitudinal variation of the Coriolis parameter [math]f[/math] can be neglected;
- frictionless tidal flow;
- tidal amplitude much smaller than depth;
- current velocities much smaller than tidal wave celerity [math]c[/math].
Tidal equations
Inclusion of Coriolis acceleration, [math]f=2\Omega \sin \phi[/math], in the tidal equations yields:
[math] \Large \frac{\partial u}{\partial t} \normalsize - f v + g \Large \frac{\partial \eta}{\partial x} \normalsize =0 ,[/math]
[math] \Large \frac{\partial v}{\partial t} \normalsize + f u + g \Large \frac{\partial \eta}{\partial y} \normalsize =0 ,[/math]
[math] \Large \frac{\partial \eta}{\partial t} \normalsize + h \; ( \Large \frac{\partial u}{\partial x} + \Large \frac{\partial v}{\partial y} \normalsize ) =0 .[/math]
The following conventions are used:
- [math]u,v[/math] are the depth-averaged tidal current velocities in [math]x,y[/math]-directions, respectively;
- [math]\eta[/math] is the tide level;
- [math]h[/math] is the average depth;
- [math]\Omega[/math] is the radial frequency of earth's rotation;
- [math]\phi[/math] is the latitude expressed in radians (positive for the northern hemisphere, negative for the southern hemisphere).
The current velocities [math]u,v[/math] can be eliminated from the tidal equations; this gives
[math]\Large \frac{\partial^2 \eta }{\partial t^2} \normalsize + f^2 \eta = gh \; (\Large \frac{\partial^2 \eta }{\partial x^2} + \frac{\partial^2 \eta }{\partial y^2} \normalsize ) . [/math]
Dispersion relation
The wave solution of the tidal equation has the form
[math] \eta(x,y,t)= A e^{\large i(k_x x+k_y y - \omega t) \normalsize} .[/math]
The physical water level elevation [math]\eta[/math] corresponds to the real part of this expression. The propagation direction is given by the real part of the vector [math]\vec k = (k_x,k_y)[/math], written as [math]\Re \vec k = (k,l)[/math], and the phase speed is given by [math]c=\omega / \sqrt{k^2+l^2} .[/math] Substitution of this solution yields the dispersion relation
[math] gh(k_x^2+k_y^2)=\omega^2-f^2 .[/math]
By choosing the [math]x[/math]-axis along the propagation direction (i.e. [math]k=\omega / c, l=0[/math]), the dispersion relation reads
[math]gh(k^2-\mu^2)=\omega^2-f^2, [/math]
where the imaginary part [math]\mu \equiv \Im k_y [/math] is the damping factor perpendicular to the propagation direction. For the tidal wave solution the corresponding velocity components are given by
[math]u = g \Large \frac{k \omega - \mu f }{\omega^2-f^2} \normalsize \Re \eta , \; v = g \Large \frac{k f - \mu \omega}{\omega^2-f^2} \normalsize \Im \eta. [/math]
At [math]x=0[/math] the velocity components are
[math]u = B c (1 - \Large \frac{\mu f c}{\omega^2} \normalsize) \cos \omega t, \; v = - B c \Large \frac{f -\mu c}{\omega} \normalsize \sin \omega t , \; B = \Large \frac{A/h} {1 -(\mu c / \omega)^2} \normalsize e^{\large -\mu y \normalsize }. [/math]
For [math]\mu c \lt f \lt \omega ,[/math] the current vector ([math]u,v[/math]) rotates anti-cyclonically around an ellipse; for [math]\mu=0[/math] the demi-axes are ([math]A \omega / kh, A|f|/kh[/math]), see figure 1.
Kelvin wave
A particular solution of the tidal equations corresponds to
[math]\mu = \Large \frac{f}{c} \normalsize , \; c=\sqrt{gh} .[/math]
For this solution, which is called Kelvin wave, we have [math] v=0[/math] and
[math] \eta(x,y,t)= A e^{\large-fy/c \normalsize } \cos(kx-\omega t) ,\; u= (Ac/h) e^{\large -fy/c \normalsize } \cos(kx-\omega t). [/math]
The Kelvin wave is a reasonable approximation for tidal waves in the vicinity of a straight coastline [math]y=y_0[/math], where [math]v \approx 0[/math].
The Kelvin wave is largest near the coastline and exponentially damped further away; it propagates along the coast with the coastline at the right hand in the northern hemisphere ([math]f,y\gt y_0[/math]) and with the coastline at the left hand in the southern hemisphere ([math]f,y\lt y_0[/math]).
Amphidromic points
A tidal wave propagating in a rectangular basin of length [math]L[/math] can be described by the sum of two Kelvin waves, an incoming wave propagating in negative [math]x[/math]-direction along the right boundary [math]y=0[/math] and a reflected wave propagating in positive [math]x[/math]-direction along the left boundary [math]y=b[/math],
[math]\eta = (A/2) \left[e^{\large f(y-b/2)/c \normalsize }\cos(kx+\omega t) + e^{\large -f(y-b/2)/c \normalsize } \cos(kx-\omega t) \right] ,[/math]
[math]u = (cA/2h) \left[e^{\large f(y-b/2)/c \normalsize }\cos(kx+\omega t) - e^{\large -f(y-b/2)/c \normalsize } \cos(kx-\omega t) \right] ,[/math]
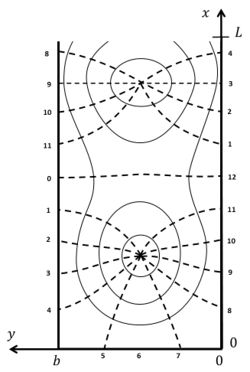
The closed landward boundary is at [math]x=0[/math] and the open seaward boundary at [math]x=L[/math]. At [math]x=\pi/2k, y=b/2[/math] the vertical wave motion is zero; this is the so-called amphidromic point. In long basins another amphidromic point exists at [math]x=3\pi/2k, y=b/2[/math]. In long wide basins the tidal wave composed of incoming and reflected Kelvin waves turns around amphidromic points, see figure 2.
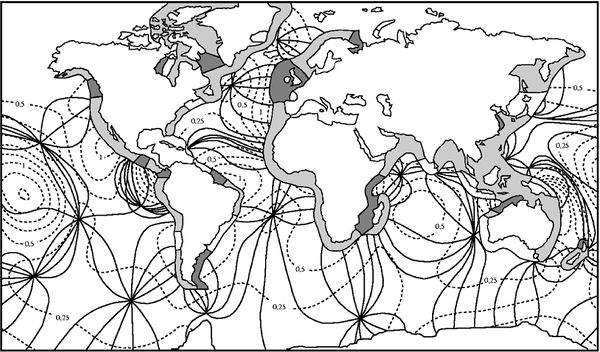
In the ocean the semidiurnal lunar tidal wave turns around amphidromic points, see figure 3. This illustrates that ocean tides can be approximately characterised by a system of Kelvin waves.
Poincaré waves
Because Kelvin waves are not a full solution of the tidal equations, the condition [math]u=0[/math] at the closed boundary [math]x=0[/math] is satisfied only for [math]y=b/2[/math]. Other wave solutions have to be taken into account near the head of the basin. These are the so-called Poincaré waves, which are periodic in the lateral coordinate [math]y[/math] in order to satisfy the condition [math]v=0[/math] at the lateral basin boundaries [math]y=(0,b) [/math],
[math]v = \sum_{n=1}^{n=\infty} (C_n e^{\large \nu_n x \normalsize } + D_n e^{\large -\nu_n x \normalsize }) \sin (\Large \frac{n \pi y }{b} \normalsize) \cos(\omega t) .[/math]
From the dispersion relation we have
[math]\nu_n^2=-k_x^2=(\Large \frac{n\pi}{b})^2- \frac{\omega^2-f^2}{gh} \normalsize .[/math]
In basins which are much narrower than the tidal wavelength, [math]\nu_n[/math] is a real positive number, [math]\nu_n \approx n \pi /b[/math]. In this case Poincaré waves are significant only near the head of the basin and strongly damped elsewhere. The contribution of the Poincaré waves to the tidal elevation can be derived by eliminating [math]u[/math] from the tidal equations. The result is
[math] \eta = \Large \frac{h}{\omega^2+gh \nu_n^2} \normalsize (f \Large \frac{\partial v}{\partial x} + \frac{\partial^2 v}{\partial y \partial t} \normalsize).[/math]
The coefficients [math]C_n,D_n[/math] are determined from the boundary conditions
[math]u_K(0,y,t)+u_P(0,y,t)=0[/math] and [math]\eta_K(L,y,t)+\eta_P(L,y,t)=\eta(L,y,t)[/math]
at the landward and seaward boundaries. The subscripts [math]K,P[/math] indicate the Kelvin and Poincaré wave contributions, respectively. The solution was first given by G.I. Taylor in 1921 [1], see figure 2.
Influence of friction
Inclusion of friction influences the tidal wave in several important ways. Analytical expressions can be derived if the tidal equations are linearised. Because calculations are quite lengthy, the reader is referred to the literature [2], [3]. Here we only mention some major consequences of the inclusion of friction terms in the tidal equations.
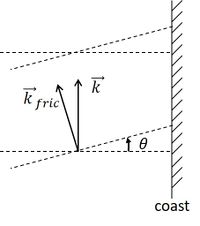
(1) The crests of Kelvin waves are not perpendicular to the coastline, but are rotated in cyclonic direction, see figure 4.
(2) The amphidromic points are not situated on the center line of semi-enclosed basins, but they are shifted in cyclonic direction relative to the propagation direction of the incoming tidal wave, see figure 5.
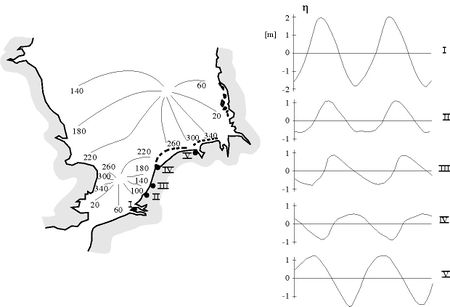
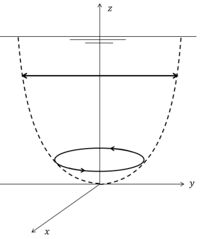
(3) The current velocity vector rotates in cyclonic direction with increasing distance from the water surface [4],[5], see figure 6. This can be shown by decomposing the tidal current in two circular rotating components, one component rotating in cyclonic direction and the other component in anticyclonic direction. If the magnitude of the two components is the same, the tidal current is rectilinear. Frictional damping depends on the rotation sense. The anticyclonic component is more strongly damped with increasing depth than the cyclonic component; the latter therefore dominates near the bottom.
(4) In shallow coastal zones, with significant tide compared to the depth, the Kelvin wave propagates faster at high tide than at low tide. The tidal wave therefore becomes increasingly distorted in the propagation direction; tidal rise becomes faster than fall. See figure 5. Fast tidal rise causes stronger flood currents than ebb currents in adjacent tidal lagoons and estuaries. This tidal asymmetry stimulates sediment import. It can result in silting up of lagoons and in the formation of turbidity maxima in estuaries.
References
- ↑ Taylor, G.I. (1922) Tidal oscillations in gulfs and rectangular basins. Proc Lond Math Soc 20:148–181
- ↑ Pedlosky, J. (1979) Geophysical Fluid Dynamics. Springer Verlag, 624 pp.
- ↑ Rienecker, M.M. and Teubner, M.D. (1980) A note on frictional effects in Taylor’s problem. J Mar Res 38(2):183–191
- ↑ Prandle, D. (1982) The vertical structure of tidal currents. Geophys. and Astrophys. Fluid Dynamics 22: 29-49
- ↑ Maas, L.R.M. and Van Haren, J.J.M. (1987) Observations on the vertical structure of tidal and inertial currents in the central North Sea. Journal of Marine Research. 45: 293-318
Please note that others may also have edited the contents of this article.
|