Proudman resonance and meteo tsunamis
Contents
Generation of meteo tsunamis
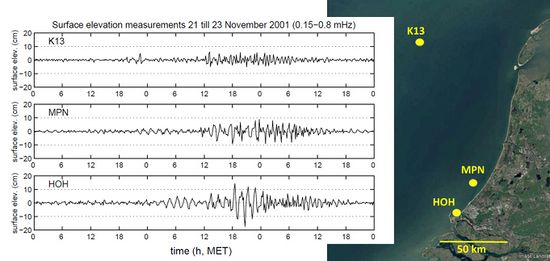
Local atmospheric pressure disturbances above open water generate wave motions at the water surface. The periods of these meteo-induced waves are typically in the range of a few minutes to a few hours, i.e. intermediate between wind waves and tidal waves. The amplitude of these waves is generally small (typically in the cm range) compared to wind waves and tidal waves. However, in some cases they can be strongly amplified. This occurs when the pressure perturbation advances at a speed comparable to the propagation speed (celerity) of the surface waves in the water body. This amplification is known as Proudman resonance, after the scientist who first demonstrated this phenomenon[2]. When meteo-induced water waves are strongly amplified they are often called meteo tsunamis, because their period is in the same range where tsunamis caused by other phenomena occur, such as submarine earthquakes and landslides – see the article Tsunami. Various atmospheric processes can generate meteo tsunamis, for example frontal passages, gales, squalls, storms, orographic influence and tornados. An example of a meteo tsunami is shown in Fig. 1.
Proudman resonance
Whether the propagation speed [math]V[/math] of an atmospheric pressure disturbance is comparable to the celerity [math]c[/math] of surface waves depends on the depth of the water body, which can be approximated by [math]c=\sqrt{gh}[/math], where [math]h[/math] is the local water depth and [math]g \approx 9.8 \, m^2 s^{-1}[/math] the gravitational acceleration. In deep ocean water the wave propagation celerity is always much larger (typically in the order of 200 m/s) than the speed of atmospheric pressure disturbances (typically in the order of 10-30 m/s). However, on the continental shelf (depths between 50 and 500 m), the speeds can be comparable and Proudman resonance can occur. The mathematical derivation by Proudman is presented in the appendix.
Harbor seiches

Proudman resonance can amplify the initial meteo-induced water wave by a factor 5-10 if the propagation speeds of the atmospheric disturbance and the water wave are about the same[3]. Even in this case the amplitude of the meteo tsunami will not exceed a few decimeters. Waves of this amplitude generally do not cause great harm. However, further amplification can occur if the wave period is close to the resonance period of coastal topographic features, such as semi-enclosed bays and basins. Many harbors resonate at wave periods in the same range as the periods of meteo tsunamis, on the order of one minute period for small harbors and on the order of one hour for large harbors (the basic resonance period of an elongate harbor of length [math]L[/math] and depth [math]h[/math] is given by [math]4L/\sqrt{gh}[/math]). If the harbor resonance period and the wave period match, a further wave amplification with a factor 5-10 is possible[4]. Resonant harbor waves are called seiches. For a more detailed discussion of this phenomenon, the reader is referred to the article Harbor resonance. Harbor seiches can cause considerable damage to berthed vessels and harbor infrastructure (Fig. 2).
Appendix: A simple mathematical model of Proudman resonance
The simple model, first described by Proudman[2], considers the following idealised situation:
- Continental shelf of uniform depth [math][/math],
- The influence of friction, tide and earth's rotation are neglected.
The pressure disturbance is assumed uniform in [math]y[/math]-direction and moves without deformation in [math]x[/math]-direction with velocity [math]V[/math]. The disturbance is then given by [math]p=-g \rho f(x-Vt)[/math], where [math]\rho[/math] is water density. The shallow-water equations of motion read
[math]\Large\frac{\partial u}{\partial t}\normalsize + g \Large\frac{\partial \zeta}{\partial x}\normalsize = - \Large\frac{1}{\rho}\frac{\partial p}{\partial x}\normalsize , \quad h\Large\frac{\partial u}{\partial x}\normalsize + \Large\frac{\partial \zeta}{\partial t}\normalsize = 0[/math].
Elimination of [math]u[/math] gives the equation [math]\Large\frac{\partial^2 \zeta}{\partial t^2}\normalsize -gh\Large\frac{\partial^2 \zeta}{\partial x^2}\normalsize = -gh\Large\frac{\partial^2 }{\partial x^2} \normalsize f(x-Vt)[/math].
The general solution reads
[math]\zeta(x,t)=\zeta^{(1)}(x-ct)+ \zeta^{(2)}(x+ct)+ \zeta^{(3)}(x-Vt), \qquad \zeta^{(3)}=\Large\frac{f}{1-(V/c)^2}\normalsize , \quad c=\sqrt{gh}[/math].
The functions [math]\zeta^{(1)}[/math] and [math]\zeta^{(2)}[/math] are determined by the initial conditions [math]\zeta=0, u=0[/math] at [math]t=0[/math]. Evaluation of these conditions yields
[math]\zeta(x,t)=\Large\frac{1}{1-(V/c)^2}\normalsize \Big[ f(x-Vt) - \Large\frac{1}{2}\normalsize (1+\Large\frac{V}{c})\normalsize f(x-ct) - \Large\frac{1}{2}\normalsize (1-\Large\frac{V}{c})\normalsize f(x+ct) \Big] [/math].
If the propagation speed of the disturbance is close to the wave celerity, [math]V =c+dc[/math], the expression of [math]\zeta[/math] can be approximated by
[math]\zeta(x,t) \approx -\Large\frac{Vt}{2}\frac{\partial}{\partial x} \normalsize f(x-VT), \qquad x \le Vt[/math].
In this case we have Proudman resonance: the amplitude of the meteo-induced wave increases linearly with time. It can be shown that this result remains qualitatively valid even if the conditions of this simple model are not strictly met[5].
Related articles
References
- ↑ De Jong, M.P.C. 2004. Origin and prediction of seiches in Rotterdam harbour basins. PhD thesis Delft University.
- ↑ 2.0 2.1 Proudman, J. 1929. The effects on the sea of changes in atmospheric pressure. Geophys J Int 2: 197–209
- ↑ 3.0 3.1 Monserrat, S., Vilibic, I. and Rabinovich, A.B. 2006. Meteotsunamis: atmospherically induced destructive ocean waves in the tsunami frequency band. Natural Hazards and Earth System Sciences 6: 1035–1051
- ↑ Rabinovich, A.B. 2009. Seiches and harbor oscillations. In: Handbook of Coastal and Ocean Engineering (Ed. Y.C. Kim). World Scientific Publ., Singapoure
- ↑ Williams, D.A., Horsburgh, K.J., Schultz, D.M. and Hughes, C.W. 2021. Proudman resonance with tides, bathymetry and variable atmospheric forcings. Natural Hazards 106: 1169–1194
Please note that others may also have edited the contents of this article.
|