Difference between revisions of "Stability models"
| Line 83: | Line 83: | ||
====3) Linearization of the governing equations.==== | ====3) Linearization of the governing equations.==== | ||
| − | The perturbations with respect to the selected equilibrium solution must be defined, <math> | + | The perturbations with respect to the selected equilibrium solution must be defined, <math>z_b'(x,y,t) = z_b(x,y,t) - z_{be}(x,y)</math>, <math>E'(x,y,t) = E(x,y,t) - E_e(x,y)</math>, etc. Then, the governing equations must be linearized by neglecting powers higher than one of those perturbations. If the perturbations in all the variables are represented by a vector <math>X(t)</math>, the linearized equations can be represented by: |
<math>\ dX(t)/dt = B \cdot X(t) </math> | <math>\ dX(t)/dt = B \cdot X(t) </math> | ||
| Line 98: | Line 98: | ||
<math>\ Z(x,y) = A e^{i (K_x x + K_y y)} </math> | <math>\ Z(x,y) = A e^{i (K_x x + K_y y)} </math> | ||
| − | where <math>A</math> is a constant vector. In this case, the eigenvalue problem can be solved algebraically leading to a complex dispersion relation, <math> \sigma = \sigma (K_x,K_y) </math>. Very often, there is uniformity in one direction, say <math>y</math>, but not in the other. This is typically the case in coastal stability problems where the equilibrium solution depends on the cross-shore coordinate, <math>x</math>, but not on the alongshore one, <math>y</math>. Thus, the eigenfunctions are wave-like only in the <math>y</math> direction and are | + | where <math>A</math> is a constant vector. In this case, the eigenvalue problem can be solved algebraically leading to a complex dispersion relation, <math> \sigma = \sigma (K_x,K_y) </math>. Very often, there is uniformity in one direction, say <math>y</math>, but not in the other. This is typically the case in coastal stability problems where the equilibrium solution depends on the cross-shore coordinate, <math>x</math>, but not on the alongshore one, <math>y</math>. Thus, the eigenfunctions are wave-like only in the <math>y</math> direction and are: |
<math>\ Z(x,y) = e^{i K_y y} F(x)</math> | <math>\ Z(x,y) = e^{i K_y y} F(x)</math> | ||
| − | In this case, solving the corresponding eigenproblem requieres solving a boundary value problem for ordinary differential equations for <math>F(x)</math> which is commonly done by numerical methods. In case where the equilibrium state has gradients in any horizontal direction the eigenproblem leads to a boundary value problem for partial differential equations | + | In this case, solving the corresponding eigenproblem requieres solving a boundary value problem for ordinary differential equations for <math>F(x)</math> which is commonly done by numerical methods. In case where the equilibrium state has gradients in any horizontal direction the eigenproblem leads to a boundary value problem for partial differential equations in <math>\ Z(x,y) </math>. |
====5) Analysis of the eigenvalue spectrum. Extracting conclusions.==== | ====5) Analysis of the eigenvalue spectrum. Extracting conclusions.==== | ||
Revision as of 10:22, 5 April 2007
Contents
- 1 Stability: concepts.
- 2 Stability methods: use in coastal sciences.
- 3 Stability methods: use in long term morphological modelling.
- 4 Linear stability models.
- 5 Nonlinear stability models.
Stability: concepts.
The concepts of equilibrium and stability come from Classical Mechanics. A state where a system is in balance with the external forcing so that it does not change in time is called an equilibrium position. However, any equilibrium position may be either stable or unstable. If released near a stable equilibrium position, the system will evolve towards such a position. On the contrary, if released near an unstable equilibrium position, it will go far away from this position. For instance, a pendulum has two equilibrium positions, one up (A), another down (B). If released at rest at any position (except at A) the pendulum will start to oscillate (if it is not already in B) and due to friction it will end up at rest at B. Thus, the pendulum will move spontaneously towards the stable equilibrium and far away from the unstable equilibrium.
Similarly, a beach under constant wave forcing is commonly assumed to reach after some time certain equilibrium profile. However, two main assumptions are here involved: i) an equilibrium state exists and ii) the equilibrium is stable. The existence of an equilibrium profile seems to be granted in the books on coastal sciences and the stability of such an equilibrium is implicitly assumed. However, even if an equilibrium profile exists, it is not necessarily stable. This means that the system would ignore such an equilibrium, it would never tend spontaneously to it. Furthermore, several equilibria may exist, some of them stable, some others unstable.
Example:
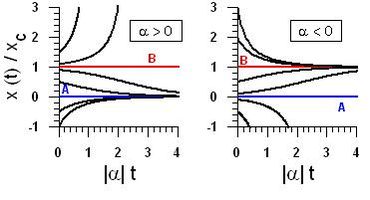
Let us assume a system which is described by only one variable as a function of time, [math]x(t)[/math], and two constant parameters [math] \alpha [/math] and [math] x_c \gt 0 [/math] which are representative of both the characteristics of the system and the external forcing. Assume that this variable is governed by the ordinary differential equation:
[math] \frac{dx}{dt} = \alpha (x-x_c)x \qquad (1) /math\gt For instance, in a coastal system, \lt math\gt \alpha [/math] could represent sediment grain size or wave height, and [math]x(t)[/math] the shoreline displacement at an alongshore location. Given an initial position [math] x(0)=x_0 [/math], the subsequent evolution of the system is described by the solution of the differential equation
[math] x(t) = \frac{x_0 x_c}{x_0 +(x_c-x_0)exp(x_c \alpha t)} \qquad (2)[/math]
It becomes clear that the system has two equilibrium positions, (A): [math]x=0[/math], and (B): [math]x=x_c[/math]. Moreover, for [math] \alpha \gt 0[/math], (A) is stable while (B) is unstable. In contrast, (A) is unstable and (B) is stable for [math] \alpha \lt 0 [/math]. This is illustrated by Fig. 1 where typical [math]x(t)[/math] solutions are plotted for various initial conditions.
Stability methods: use in coastal sciences.
Coastal and Geomorphic systems exhibit patterns both in space and time. Some of these patterns directly obey similar patterns in the external forcing. For example, a beach profile may erode and subsequently recover directly in response to the cycle storm/calm weather in the external wave forcing with the same time scale. This is known as forced behaviour. Other patterns, even if they are driven by some external forcing, do not resemble similar patterns in the forcing. For instance, although bed ripples may be originated by a unidirectional current over a sandy bed, there is nothing in the current itself which dictates the shape, the lengthscale or the characteristic growth time of the ripples. The ripples constitute a new pattern which is not present in the forcing. This is called free behaviour or self-organized behaviour. The forced behaviour is much simpler to predict once the forcing is known. In contrast, predicting the free behaviour is typically much more complicated as it involves the complex internal dynamics of the system itself.
Stability methods are the genuine tool to describe, understand and model pattern formation by self-organization. The typical procedure is to start considering an equilibrium of the system where the pattern is absent (for instance, flat bed, in case of ripples). The key point is that small fluctuations or irregularities are always present (a perfect flat bed or an exact unidirectional, uniform and steady current do not exist). Then, if the equilibrium is stable, any initial small perturbation of the equilibrium will dye away in time. Thus, those small fluctuations will not succeed in driving the system far from the equilibrium (the bed will keep approximately flat). However, if the equilibrium is unstable, there will exist initial perturbations that will tend to grow. Among all of them, some will grow faster than others and their characteristics will prevail in the state of the system. In other words, the patterns corresponding to these initially dominant perturbations of the equilibrium will emerge and will explain the occurrence of the observed patterns (the ripples). However, different patterns may emerge during the instability process and the finally dominant one (the one which is observed) may not correspond to the initially dominant.
Stability methods have been applied to understand the origin and dynamics of many coastal features. A first example are the shear or vorticity waves in the surf zone. These are low frequency waves which are not gravity waves but are originated from the wave-driven longshore current. Their wavelength is a few times the width of the surf zone, their period is of a few minutes an they propagate with a celerity which is a fraction of the peak longshore current. Their occurrence can be explained as a hydrodynamic instability (i.e., bed changes are not essential) as follows. One may consider a rectilinear coast with an alongshore uniform bathymetry and an alongshore uniform wave forcing (with shore oblique incidence). Then, an alongshore uniform current along with a uniform set-up/set-down is an equilibrium state of the system (mean wave-averaged hydrodynamics). If the current shear is small in comparison with bed friction and turbulent lateral mixing, the equilibrium is stable. However, if it is strong enough, the current becomes unstable and the instability leads to the growth of shear waves. The final result may be a meandering and pulsating longshore current with the wavelength and period of shear waves.
When applied to the formation of morphological patterns the instability which leads to the growth is typically originated by a positive feedback between the evolving morphology and the hydrodynamics. This can operate at different scales and in various environments. The oscillatory flow of waves over a flat sandy bed moves the sand back and forth without a net displacement. Therefore, this constitutes an equilibrium of the water-sediment system. However, if a small undulation is given to the bed, this originates vortex flow in a vertical plane which is able of pilling up the sand over the crest of the undulation. If this tendency is stronger than gravity the flat bed will be unstable and ripples will develop from such an instability. Similarly, a unidirectional and steady current over a flat bed transports sediment but if there are no longitudinal gradients there is neither erosion nor deposition: the water-sediment system is in equilibrium. But any perturbation given to the bottom will disturb the water flow thereby causing longitudinal gradients in sediment flux. If the gradients are so that there is convergence at the shallows and/or divergence at the deeps, the topographic perturbation will tend to grow. If this growth reinforces the hydrodynamic perturbation a positive feedback between the bed form and the flow will occur and the flat bed and uniform current will be unstable. This instability may lead the formation of hydraulic dunes.
Beach cusps are topographic undulations at the swash zone of some beaches. They are intriguing mainly because their striking regularity and alongshore periodicity. There is a number of potential explanations for their origin, including edge wave forcing. However, their origin by self-organization has become more and more plausible in recent years. According to it, an alongshore uniform swash zone is in equilibrium with an alongshore uniform wave forcing. If small undulations are superimposed on the equilibrium topography, the uprush and run-down will no longer be uniform: the hills will deflect the uprush and the run-down will be stronger at the depressions. If this flow pattern erodes the depressions and deposits sand an the hills, a positive feedback will occur thereby de-stabilizing the equilibrium and making the cusps to emerge.
At a length scale larger than that of ripples, dunes and cusps, the surf zone may also exhibit a variety of morphological patterns which are commonly known as rhythmic features because they are periodic or nearly periodic alongshore. Their alongshore spacing is of the order of one to a few times the surf zone width, i.e., typically from tens to hundreds of meters, up to maybe one-two km's. A very common source of such patterns is a meandering shore parallel bar which is called crescentic bar. The deepest sections of such a bar are called rip channels. The shallowest sections tend to approach the shore and sometimes attach to it. At the attachment points, the coastline becomes cuspate and this defines what are called mega-cusps. They are different from the 'ordinary' cusps in that those are associated to the shoals at the attachment points which are called transverse bars. However, transverse bars may also exist as elongated shoals connected to the shore (at the corresponding mega-cusps) without any relation with crescentic bars. If their orientation is not exactly shore-normal they are called oblique bars.
Although the origin of crescentic bars and other rhythmic bars was related to the forcing by edge waves, many recent studies point to its formation by self-organization of the coupling between bathymetry, waves and currents in the surf zone. A basic state is assumed where the coastline is rectilinear and the bathymetry is alongshore uniform, either unbarred or with one or more shore-parallel bars. Wave incidence may be shore-normal, with some angle or even with directional spreading. The wave field is assumed to be constant in time. Since the cross-shore profile is assumed to be an equilibrium profile there is no cross-shore net sediment transport. Even if there is longshore transport due to wave obliquity there are no gradients in such transport so that the morphology is constant in time. This is an equilibrium state of the coupling between morphology, wave field and mean hydrodynamics. Now, this equilibrium may be stable or unstable. This means that given a small perturbation on the bathymetry, the wave field will be altered (changes in wave energy distribution, wave breaking, shoaling, refraction, diffraction, etc.), hence the mean hydrodynamics will be altered too (changes in the currents, in set-up/set-down). Therefore, there will be changes in sediment transport thereby appearing convergences/divergences of sediment flux and morphological changes. Now, these morphological changes may either reinforce or damp the initial perturbation. If the latter happens for any perturbation one may consider, the equilibrium is stable and the bathymetry will keep alongshore uniform. If the former happens for at least one possible perturbation, the equilibrium is unstable and the beach will 'spontaneously' (i.e., from the small fluctuations) develop coupled patterns in the morphology, the wave field and the mean hydrodynamics other than the featureless equilibrium. These patterns may eventually result in the observed rhythmic bars with the corresponding circulation patterns. This has been shown for the case of crescentic bars and transverse/oblique bars.
Stability methods can be used not only to understand and model naturally occurring features but also to analize the efficiency and impact of human interventions. The sand which is dumped in a shoreface nourishment interacts with the natural nearshore bars and may trigger some of the morphodynamic instability modes of the system. Following this idea, Dodd??? has applied a morphodynamic stability analysis to assess the efficiency of different shoreface nourishment strategies.
At a scale which is similar to that of rhythmic surf zone bars, the so-called free bars in rivers and estuaries can be originated from an instability of the flat bed and unidirectional current equilibrium.
Stability methods: use in long term morphological modelling.
Continental shelf morphologic features
The sea bed of the continental shelf is rarely flat. Rather, it is usually covered by a number of different types of morphological features ranging from megaripples to sand waves and sand banks. The latter two may be considered as long term features since the characteristic time for its formation and evolution is of decades or centuries. Their horizontal lengthscale (size and spacing) is of the order of hundreds of m for sand waves and few km's for the sand banks. Their origin has been explained as a morphodynamic instability of the coupling between the sandy bed and the tidal currents. The equilibrium situation is the flat bed where the tides do not create any gradient in sediment flux. The instability mechanism involves only depth averaged flow in case of sand banks whereas it is related to net vertical circulation cells in case of sand waves. Sand banks may also appear near the coast, in water depths of 5-20 m. In this case they are known as shoreface-connected sand ridges. Their origin has also been explained from an instability but where the tidal currents have little influence. In this case, the instability mechanism is caused by the storm driven coastal currents in combination with a transversely sloping sea bed.
Tidal inlets
Large scale shoreline instabilities
Shorelines characterized by a wave climate with high incidence angle with respect to the shore-normal commonly show a wavy shape, cuspate landforms and spits [[1]]. This can be interpreted as a result of a coastline instability. The littoral drift or total alongshore sediment transport driven by the breaking waves, [math]Q[/math], is a function of wave incidence angle with respect to the shore-normal in deep water, [math]\theta[/math]. It is zero for [math]\theta=0[/math], increases up to maximum for about [math]\theta=\theta_c=43^o[/math] and decreases down to zero for [math]\theta=90^o[/math]. The equilibrium situation is a rectilinear coastline with alongshore uniform nearshore bathymetry and alongshore uniform wave forcing with a [math]\theta[/math] angle. Assume now a small undulation of the otherwise rectilinear coastline consisting of a cuspate foreland. The wave obliquity with respect to the local shoreline is larger at the downdrift side than at the updrift side. Then, if [math]\theta \lt \theta_c[/math], higher obliquity means higher transport so that there will be larger sediment flux at the downdrift side than at the updrift side. This will erode the cuspate shape and the shoreline will come back to the rectilinear equilibrium shape. The shoreline is stable. The contrary will happen if [math]\theta \gt \theta_c[/math] so that the shoreline will be unstable in this case. The instability tends to create undulations of the coastline (shoreline sand waves) with an initial wavelength of about 1-10 km's with a characteristic growth time of the order of a few years. Once the initial undulations have grown, the shoreline may evolve towards larger wavelengths and very complex shapes including hooked spits.
Linear stability models.
The equations governing coastal systems are typically nonlinear and it is difficult to solve them or to extract useful information from them. However, the small departures from an equilibrium situation approximately obey linear equations that are very useful to determine whether the equilibrium is stable or unstable and, in the latter case, which are the emerging patterns and how fast they grow at the initial stage. For instance, for the equilibrium B ([math]x=x_c[/math]) for equation (1), one may define the departure from equilibrium, [math]z(t)=x(t)-x_c[/math], with governing equation:
[math]\frac{dz}{dt} = \alpha (x_c+z)z \simeq \alpha x_c z[/math],
where the last approximation is valid for [math]z \ll x_c [/math] and is called linearization. The approximate equation is linear in [math]z(t)[/math] and it is immediately solved to give:
[math]z(t) = z(0) e^{\sigma t}[/math],
where [math]\sigma = \alpha x_c [/math] is called the growthrate and determines whether the perturbation of equilibrium will grow or decay. We recover that B is stable if [math]\alpha \lt 0 [/math] and unstable if [math]\alpha \gt 0 [/math] without solving the nonlinear equation (1).
Typical steps in developing and using a linear stability model.
1) Governing equations.
The first step is to define the variables describing the state of the system. These may be the level of the sea bed as a function of two horizontal coordinates and time, [math]z_b(x,y,t)[/math], or the wave energy density field, [math]E(x,y,t)[/math], or the position of the coastline as a function of a longitudinal coordinate and time, [math] x_s (y,t)[/math], etc. Then, equations expressing the time derivatives of those variables must be derived. For coastal morphodynamic problems these typically constitute a system of partial differential equations in [math]x,y,t[/math].
2) Equilibrium state.
An equilibrium solution of the governing solutions where all the variables of the system are constant in time, i.e., [math]\partial z_b(x,y,t)/\partial t = 0[/math], [math]\partial E(x,y,t)/\partial t = 0[/math], etc. , must be selected.
3) Linearization of the governing equations.
The perturbations with respect to the selected equilibrium solution must be defined, [math]z_b'(x,y,t) = z_b(x,y,t) - z_{be}(x,y)[/math], [math]E'(x,y,t) = E(x,y,t) - E_e(x,y)[/math], etc. Then, the governing equations must be linearized by neglecting powers higher than one of those perturbations. If the perturbations in all the variables are represented by a vector [math]X(t)[/math], the linearized equations can be represented by:
[math]\ dX(t)/dt = B \cdot X(t) [/math]
where [math]B[/math] is a linear operator typically involving partial derivatives with respect to the horizontal coordinates, [math]x, y [/math].
4) Solving the linearized equations. Eigenvalue problem.
Since the coefficients of the linearized equations do not depend on time, solutions can be found as
[math]\ X(t) = e^{\sigma t} \, Z(x,y) [/math]
where [math]\sigma [/math] and [math]Z(x,y)[/math] are eigenvalues and associated eigenfunctions of operator [math]B[/math] (note that [math]Z[/math] is [math]n[/math]-dimensional, where [math]n[/math] is the number of variables describing our system). These eigenvalues and eigenfunctions may be complex and only the real part of the latter expression has physical meaning. The equations corresponding to the eigenproblem are partial differential equations in [math]x,y[/math]. In case where the equilibrium solution is uniform in both [math]x,y[/math] directions (e.g. stability of horizontal flat bed in an open ocean), the coefficients do not depend on these coordinates and wave-like solutions may be found as
[math]\ Z(x,y) = A e^{i (K_x x + K_y y)} [/math]
where [math]A[/math] is a constant vector. In this case, the eigenvalue problem can be solved algebraically leading to a complex dispersion relation, [math] \sigma = \sigma (K_x,K_y) [/math]. Very often, there is uniformity in one direction, say [math]y[/math], but not in the other. This is typically the case in coastal stability problems where the equilibrium solution depends on the cross-shore coordinate, [math]x[/math], but not on the alongshore one, [math]y[/math]. Thus, the eigenfunctions are wave-like only in the [math]y[/math] direction and are:
[math]\ Z(x,y) = e^{i K_y y} F(x)[/math]
In this case, solving the corresponding eigenproblem requieres solving a boundary value problem for ordinary differential equations for [math]F(x)[/math] which is commonly done by numerical methods. In case where the equilibrium state has gradients in any horizontal direction the eigenproblem leads to a boundary value problem for partial differential equations in [math]\ Z(x,y) [/math].
5) Analysis of the eigenvalue spectrum. Extracting conclusions.
The real part of [math]\sigma [/math] determines the growth or decay of the associated

