Difference between revisions of "Testpage2"
Dronkers J (talk | contribs) (Blanked the page) |
Dronkers J (talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | Tsunami | ||
| + | |||
| + | {{Definition|title=Tsunami | ||
| + | |definition= Series of long waves caused by a strong local disturbance of the water mass. The wavelength is typically much larger than the wavelength of wind-generated waves and much smaller than the wavelength of tidal waves. }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Tsunami causes and occurrence== | ||
| + | |||
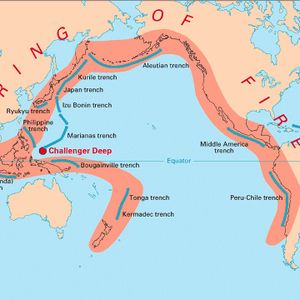
| + | [[Image:RingofFireUSGS.jpg|thumb|300px|left|Figure 1: Ring of fire around the Pacific. Image USGS.]] | ||
| + | |||
| + | The occurrence of a tsunami can have several causes<ref name=RV>Röbke, R.B. and Vött, A. 2017. The tsunami phenomenon. Progress in Oceanography 159: 296–322</ref>. The main cause, responsible for the strongest tsunamis, are seaquakes (submarine earthquakes): the sudden uplift of the seabed due to shifting earth plates. This mainly occurs in subduction zones, where an earth plate slides under an adjacent earth plate causing vertical motion of the submarine crust along the subduction line. The most important subduction zones lie along the edges of the Pacific Ocean, the so-called ring of fire (see Fig. 1). The strength of the tsunami depends not only on the vertical and horizontal size of the seafloor uplift, but also on the speed at which the seafloor rises. The strongest response occurs when this speed is comparable to the local wave propagation speed. The tsunami wave radiates in both directions perpendicular to the subduction line. | ||
| + | |||
| + | A second important cause is submarine gravity mass wasting. Such slides can be triggered by seismic activity at a sloping seabed (e.g., the shelf break) that is covered with a thick layer of unconsolidated material. The tsunami wave propagates in the direction of the slide and is strongest if the speed of the debris flow is comparable to local wave propagation speed. Gas formation (methane) due to the anaerobic degradation of organic material can contribute to the loss of stability of the sediment layer on the sloping seabed <ref>Tinivella, U., Accaino, F. and della Vedova, B. 2008. Gas hydrates and active mud volcanism on the south Shetland continental margin, Antarctic Peninsula. Geo-Mar. Lett. 28: 97–106</ref>. | ||
| + | Volcanic activity and subaerial landslides can also cause tsunamis, but these are usually not as strong. A tsunami can in rare cases result from the impact of a large meteorite. | ||
| + | |||
| + | Another type of tsunamis, so-called meteotsunamis, can arise from atmospheric disturbances. Sudden local pressure fluctuations can generate a small setup or set-down of the water level that is amplified if the atmospheric front propagates at a speed comparable to the wave propagation speed or if the spatial/temporal scales coincide <ref>Monserrat, S., Vilibić, I. and Rabinovich, A.B. 2006. Meteotsunamis: atmospherically induced destructive ocean waves in the tsunami frequency band. Nat. Hazards Earth Syst. Sci. 6: 1035–1051</ref>. The amplitude of meteotsunamis is usually small, but it can increase strongly due to resonance effects in semi-closed basins (e.g., harbor seiches, which are damaging for moored ships). | ||
| + | |||
| + | |||
| + | ==Tsunami characteristics== | ||
| + | A tsunami usually consists of a number of waves (up to about ten) of different amplitude <ref>Grilli, S.T., Harris, J.C., Tajalli Bakhsh, T.S., Masterlark, T.L., Kyriakopoulos, C., Kirby, J.T. and Shi, F. 2013. Numerical simulation of the 2011 Tohoku tsunami based on a new transient FEM Co-seismic source: comparison to far- and near-field observations. Pure Appl. Geophys. 170: 1333–1359</ref>. The third, fourth or fifth wave are often the highest <ref> Murty, T.S. 1977. Seismic sea waves. Tsunamis. In: Stevenson, J.C. (Ed.), Bulletin of the Fisheries Research Board of Canada, vol. 198</ref>. The characteristic wave period is different for each tsunami, but usually much greater than the period of wind-driven waves (i.e., more than a few minutes) and much smaller than the tidal period (i.e., less than two hours). The wave height can be a few meters at the place of origin, but when the tsunami starts propagating over the ocean the wave height quickly becomes smaller and is then usually less than one meter<ref> Bolt, B.A., Horn, W.L., Macdonald, G.A. and Scott, R.F. 1975. Geological hazards. Earthquakes—Tsunamis—Volcanoes—Avalanches—Landslides—Floods. Springer, New York</ref>. The wavelength is much greater than the water depth and the energy loss during ocean propagation is small (approximately inversely proportional to the wavelength). The propagation speed <math>c</math> can therefore be approximated with the formula <math>c = \sqrt {gD}</math>, where <math>D</math> is the average depth and <math> g </math> the gravitational acceleration. Tsunamis travel at great speed across the ocean (<math>c</math> in the order of a few hundred m/s) covering distances of many thousands of kilometers without great energy loss. | ||
| + | The energy flux <math> F </math> can be estimated with the formula <math>F = cE \approx (1/8) \rho g H ^ 2 \sqrt {gD}</math>, where <math>E</math> is the tsunami wave energy, <math> H </math> the tsunami wave height and <math>\rho</math> the water density. When the tsunami reaches the coastal zone, the water depth decreases sharply as does the propagation speed <math> c </math>. However, frictional energy dissipation being relatively modest, the energy flux <math>F</math> remains almost the same. This implies <math>H_{shore}/H_{ocean} \approx (D_{ocean}/D_{shore})^{1/4}</math>: the wave height <math>H</math> of the tsunami is strongly increased, up to about 5 times the wave height on the ocean. The wave height can be amplified even more in marine inlets, such as bays, fjords or harbours, where the tsunami energy flux is concentrated and accelerated due to strong funnel effects <ref name=RV></ref>. The tsunami waves are also distorted when entering shallow water; when the rear of the wave train is still traveling in deeper water it gets closer to the front of the wave train which is already travelling in shallow water. Differences in propagation speed of wave crest and wave trough contribute to steepening of the wave front on wide continental shelfs - wide compared to the tsunami wavelength. | ||
| + | |||
| + | When the tsunami wave arrives at the coast it runs up the shoreface (schematically depicted in Fig. 6). If the slope is steep (the width of the shoreface being much smaller than the wavelength of the tsunami, i.e. less than 10 km), the tsunami 'feels' the shoreface as a straight wall. The tsunami is then almost completely reflected and the wave height is doubled. The tsunami floods the coast as a surging wave with a relatively low speed that can be outrun. The wave run-up is not much higher than the wave height on the foreshore. | ||
| + | |||
| + | [[Image:Tsunami Phuket 2004.png|thumb|400px|left|Figure 2: The Indian Ocean tsunami of December 26, 2004, invading the coast at Phuket Thailand as a breaking bore. Picture from a camera lost on the beach. Image Flickr creative commons.]] | ||
| + | |||
| + | |||
| + | |||
| + | If the shoreface slope is gentle (the length of the foreshore being of the same order or greater than the wavelength), the tsunami transforms into an undular bore, with short waves riding on the main tsunami wave. When reaching the shore, the tsunami transforms further into a breaking bore (a wall of water, see Fig. 2) that propagates at great speed with a very fast rising water level. The wave run-up is much higher than the wave height at the toe of the shoreface (a factor of 2 and possibly more). | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | The above qualitative description suggests that the character of a tsunami is related to the surf similarity parameter <math>\xi</math> <ref name=MG> McGovern, D.J., Robinson, T., Chandler, I.D., Allsop, W. and Rossetto, T. 2018. Pneumatic long-wave generation of tsunami-length waveforms and their runup Coastal Engineering 138: 80–97</ref><ref name=LF>Larsen, B.E. and Fuhrman, D.R. 2019. Full-scale CFD simulation of tsunamis. Part 1: Model validation and run-up Coastal Engineering 151: 22–41</ref><ref name=MS>Madsen, P.A. and Schäffer, H.A. 2010. Analytical solutions for tsunami runup on a plane beach. J. Fluid Mech. 645: 27–57</ref>, | ||
| + | |||
| + | <math>\xi = \Large\frac{S}{\sqrt{2 A_0/L_{\infty}}}\normalsize = \Large\frac{S}{\omega} \sqrt{\frac{\pi g}{A_0}}\normalsize , </math> | ||
| + | |||
| + | where <math>A_0</math> is the tsunami wave height above mean sea level at the toe of the shoreface slope, <math>L_{\infty} = g T^2/(2 \pi)</math> is the tsunami wave length at infinite depth, <math>S</math> is the shoreface slope and <math>\omega</math> is the tsunami wave period. Surging waves correspond to high values of <math>\xi</math> and breaking waves to low values. | ||
| + | |||
| + | [[Image:BandAcehTsunamiLeadingDepression.jpg|thumb|300px|left|Figure 3: Retreating shoreline before arrival of the major wave of the Indian Ocean tsunami at Banda Aceh on December 26, 2004. Image C.E. Synolakis <ref name=SB>Synolakis, C.E. and Bernard, E.N. 2006. Tsunami science before and beyond Boxing Day 2004. Phil. Trans. R. Soc. A. 364: 2231–2265</ref>.]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | A distinction is often made between two types of tsunamis: tsunamis where the largest wave crest precedes the largest wave trough (sometimes called leading-elevation N-wave or LEN-wave) and tsunamis where the largest wave crest is preceded by the largest wave trough (sometimes called leading-depression N-wave or LDN-wave). Both types of tsunami occur in practice. In case of a LDN-wave, the sea retreats over a large distance and part of the shoreface falls dry before arrival of the wave crest, see Fig. 3. This is an important signal for bathers that a high tsunami wave is approaching. A LDN-wave approaches the shore at a lower speed than a similar LEN-wave, but the runup speed on land is in both cases of the same order. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Tsunami impact== | ||
| + | Tsunamis can cause enormous damage to coastal infrastructure, crushing houses, deracinating trees and making many casualties, see Fig. 4. From historical records it has been estimated that more than a million people have been killed worldwide by tsunamis <ref>National Geophysical Data Center/World Data Service, 2015. Global historical tsunami database. Tsunami event data. <http://www.ngdc.noaa.gov/hazard/tsu_db.shtml></ref>. In low-lying coastal areas (less than 10 m elevation above mean sea level) tsunamis can penetrate several kilometers inland. There are even records of tsunamis that have penetrated several tens of kilometers inland and have reached levels of several tens of meters. The flood water volume is approximately equal to the water volume above beach level of the incident tsunami wave <ref>Bryant, E.A., 2008. Tsunami: The Underrated Hazard, second ed. Springer, Berlin</ref>. Runup velocities of strong tsunamis are very high; velocities of the order of 5 – 8 m/s are common and speeds up to 20 m/s have even be observed<ref>Nanayama, F. and Shigeno, K. 2006. Inflow and outflow facies from the 1993 tsunami in southwest Hokkaido. Sed. Geol. 187: 139–158</ref>. The destructive power of tsunamis is largely due to the many debris that are dragged by the flow. Upon travelling inland the flow gradually slows down. The largest debris are deposited first whereas the finest sediments are transported further inland. Sedimentary records showing upward fining deposits over large distances are a distinctive mark of tsunami events. The return flow to the sea (backwash) can also be very strong and dangerous; it follows the strongest topographic slope and is often concentrated in channels, with velocities that are often higher than during the uprush <ref>Le Roux, J.P. and Vargas, G. 2005. Hydraulic behavior of tsunami backflows: insights from their modern and ancient deposits. Environ. Geol. 49: 65–75</ref>. | ||
| + | |||
| + | {| border="0" | ||
| + | |- | ||
| + | | valign="top"| | ||
| + | [[File:Tsunami Phuket 2004 S.Kennedy.jpg|thumb|left|300px|Fig. 4a. Impact of the Indian Ocean tsunami of December 26, 2004 at Phuket, Thailand. Image S. Kennedy, Flickr creative commons.]] | ||
| + | | valign="top"| | ||
| + | [[File:Tsunami Japan 2011 Flickr J.Teramoto.jpg|thumb|left|300px|Fig. 4b. Destruction at the Honshu coast, Japan, by the tsunami of March 11, 2011. Image J. Teramoto, Flickr creative commons.]] | ||
| + | | valign="top"| | ||
| + | [[File:Tsunami Japan 2011 S.Yoshida.jpg|thumb|left|300px|Fig. 4c. Destruction at the Honshu coast, Japan, by the tsunami of March 11, 2011. Image Y. Yoshida, Flickr creative commons.]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==Why are tsunamis so devastating== | ||
| + | The period of tsunami waves is typically in the range 300 – 6000 s (angular frequency in the order of 0.001 – 0.02 <math>s^{-1}</math>). Therefore, these waves are rather insensitive to the effect of earth's rotation, which corresponds to a frequency smaller than 0.00015 <math>s^{-1}</math>. Tsunami waves in the ocean have wavelengths typically in the order of 100 to 500 km and on the continental shelf in the order of 1 – 10 km. This implies that they are refracted and diffracted by seabed structures with spatial scales of these orders of magnitude. More specifically, this means that tsunami waves refract to the continental shelf and approach the shore more or less perpendicularly. The energy flux of tsunami waves is thus directed toward the coast. This contrasts with tidal waves that are too long for being refracted to the coast. Due to their very low frequency, tidal waves are bent along the coast by the effect of earth's rotation (see [[Coriolis and tidal motion in shelf seas]]). The energy flux of tidal waves, which is comparable in strength to the energy flux of tsunami waves, is therefore not directed towards the coast, but along the coast. Hence, the impact of tidal waves on the coast is much less than the impact of tsunami waves. | ||
| + | Just like tsunami waves, wind-generated waves are also refracted to the coast. Their energy density on the ocean is generally higher than the energy density of tsunami waves. However, the energy propagation speed of wind waves is much lower and so is the corresponding energy flux. Hence, wind waves are much less amplified when travelling into shallow water than tsunami waves. Moreover, wind waves lose a great deal of their energy due to breaking in the surf zone before they reach the shore. This explains why tsunamis have a far more devastating effect on the coast compared to tidal and wind waves. | ||
| + | |||
| + | |||
| + | ==Tsunami observation and warning== | ||
| + | Experimental measurements of real-life tsunamis running up the coast do not exist. Installing observation equipment at specific locations in anticipation of a tsunami makes no sense. Tsunami's are very rare events for each specific coastal location, even in areas that are very sensitive to submarine earthquakes. Experimental information about tsunamis that actually occurred is based on the effects observed in the coastal area after being hit by a tsunami. In some cases, eyewitness reports or amateur films are available. Although very important, this is insufficient for gaining in-depth understanding of the hydrodynamic processes that occur when a tsunami hits the coast. For this reason, understanding tsunamis is primarily based on modelling, as described in the next section. | ||
| + | |||
| + | Tectonic activity that generates tsunamis is recorded by many seismic stations around the world. However, submarine earthquakes do not necessarily cause a tsunami. Tsunamis traveling across the ocean are very long waves of small amplitude that cannot be easily detected visually or by ships. For tsunami warning, an extensive network of monitoring stations has been installed in ocean areas where tsunamis can occur. The largest network is the DART system <ref> Deep-ocean Assessment and Reporting of Tsunamis, https://www.ndbc.noaa.gov/dart/dart.shtml </ref> consisting of an array of stations in the Pacific Ocean, see fig. 5a. Each station consists of a seabed pressure recorder that detects the passage of a tsunami. The data is sent by sonar signal to a moored buoy. This buoy sends a radio signal via satellite to the Pacific Tsunami Warning Center, see Fig. 5b. In this way, a tsunami traveling across the ocean can be detected and an early warning can be issued to countries where the tsunami will land, allowing timely evacuation of risk populations. The information collected by the monitoring network also enables to estimate the nature and intensity of the tsunami and the possible impact on the coast. | ||
| + | |||
| + | {| border="0" | ||
| + | |- | ||
| + | | valign="top"| | ||
| + | [[File:TsunamiMonitoringNetwork.jpg|thumb|left|400px|Fig. 5a. The global tsunami monitoring network.]] | ||
| + | | valign="top"| | ||
| + | [[File:TsunamiWarningDARTsystem.png|thumb|left|400px|Fig. 5b. The DART monitoring system. Image NOAA.]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==Tsunami models== | ||
| + | Due to the lack of field observations, one has to rely on models for gaining insight into the hydrodynamic processes involved in tsunami events. The propagation of tsunami waves over the continental shelf and the shoreface can be simulated in hydraulic scale models based on Froude scaling, as long as boundary-layer processes are of minor importance. Scale effects occur when energy dissipation (wave breaking, bed friction) comes into play. This imposes a limitation on the simulation of the inland runup process in the laboratory. The same limitation applies to simple mathematical models that do not include wave breaking and friction. Detailed process-based numerical models are required for simulating these effects. A thorough model study of this type has been carried out by Larsen and Furman (2019)<ref name=LF></ref>. | ||
| + | |||
| + | A major problem for predicting the impact of tsunamis lies in the fact that the initial tsunami-generating disturbance cannot be predicted and is generally not well known. When a tsunami wave is detected on the ocean, the time is too short for an accurate calculation of the impact before the tsunami lands on the coast. Only theoretical or semi-empirical relationships can be used. | ||
| + | |||
| + | [[Image:TsunamiScheme.jpg|thumb|400px|left|Figure 6: Schematization of the shoreface and beach used in the tsunami runup model of Madsen and Schäfer (2010)<ref name=MS></ref>.]] | ||
| + | |||
| + | Relationships for the tsunami runup height and runup velocity, validated with laboratory experiments and advanced numerical models, are based on the theoretical work of Madsen and Schäfer (2010)<ref name=MS></ref>. They solved analytically the non-linear shallow-water equations (mass and momentum balance) over a sloping bed, | ||
| + | |||
| + | <math>\Large\frac{\partial \zeta}{\partial t}\normalsize + \Large\frac{\partial}{\partial x}\normalsize [(D+\zeta -Sx)u] = 0 , \quad \Large\frac{\partial u}{\partial t}\normalsize + u \Large\frac{\partial u}{\partial x}\normalsize + g \Large\frac{\partial \zeta}{\partial x}\normalsize =0 , </math> | ||
| + | |||
| + | where <math>t</math> is time, <math>x</math> is the spatial coordinate in the propagation direction, <math>D</math> is the average shelf depth, <math>S</math> is the average shoreface and beach slope, <math>\zeta</math> is the surface elevation and <math>u</math> is the depth-averaged current velocity. The corresponding schematization is shown in Fig. 6. Madsen and Schäfer considered an incident tsunami wave of the form | ||
| + | |||
| + | <math>\zeta(0,t) = A_0 \cos(\omega t) .</math> | ||
| + | |||
| + | For a non-breaking tsunami wave they arrived at the following expressions for the maximum runup height <math>R</math> and the maximum runup velocity <math>V</math>: | ||
| + | |||
| + | <math>R = 2 \pi^{3/4} A_0 (D / A_0)^{1/4} \xi^{-1/2} , \quad V = 2 \pi^{5/4} (A_0 / D) \sqrt{g A_0} \xi^{-3/2} . </math> | ||
| + | |||
| + | These simple expressions represent fairly well detailed numerical model results that include wave breaking, bed friction and turbulent energy dissipation<ref name=LF></ref>. The numerical model gives somewhat higher values of <math>R</math> and <math>V</math>, but in practice the values might be lower due to energy dissipation on obstacles that are generally present the runup area. | ||
| + | |||
| + | The numerical model <ref name=LF></ref> also provides results for <math>R</math> and <math>V</math> in the case of a breaking tsunami. These results are best approximated by | ||
| + | |||
| + | <math>R = A_0 \xi , \quad V = 2 \sqrt{g A_0} .</math> | ||
| + | |||
| + | The first expression corresponds to the formula established by Hunt (1959) <ref>Hunt, I.A. 1959. Design of seawalls and breakwaters. J. Waterw. Harbors Division ASCE 85: 123–152</ref> for swash uprush (see the article [[Swash zone dynamics]]) and the second expression corresponds to the initial flow velocity after dam break (see the article [[Dam break flow]]). | ||
| + | |||
| + | Non-breaking tsunamis occur for large <math>\xi</math>-values <math>\xi > \xi_b</math>, corresponding to a steep shoreface/beach slope and long-period tsunamis. Breaking tsunamis occur for small <math>\xi</math>-values <math>\xi < \xi_b</math>, corresponding to gentle shoreface/beach slope and short-period tsunamis. According to the numerical model <ref name=LF></ref>, <math>\xi_b \approx 3 (D / A_0)^{1/6}</math>. | ||
| + | |||
| + | The above relationships are the result of recent studies (up to 2019) of tsunami irruption on a coast. However, further underpinning of the above results is needed, given that previous investigations produce results that differ in some respects <ref name=MG></ref>. Synolakis <ref> Synolakis, C. E. 1987. The runup of solitary waves. J. Fluid Mech. 185: 523–545 </ref> modeled the tsunami as a solitary wave of height <math>H</math>. This model, which was validated with other laboratory measurements, yields for the runup height of a tsunami the relationship | ||
| + | |||
| + | <math>R = 2.8 H S (H/D)^{5/4} .</math> | ||
| + | |||
| + | A purely empirical rule for the maximum runup of a tsunami was proposed by Plafker (1964, unpublised). This rule states that the maximum runup will not exceed twice the height of the seafloor deformation resulting from a submarine earthquake <ref name=SB></ref>. | ||
| + | |||
| + | |||
| + | ==Related articles== | ||
| + | : [[Swash zone dynamics]] | ||
| + | : [[Dam break flow]] | ||
| + | : [[Tidal bore dynamics]] | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | <references/> | ||
Revision as of 00:09, 14 January 2020
Tsunami
Definition of Tsunami:
Series of long waves caused by a strong local disturbance of the water mass. The wavelength is typically much larger than the wavelength of wind-generated waves and much smaller than the wavelength of tidal waves.
This is the common definition for Tsunami, other definitions can be discussed in the article
|
Contents
Tsunami causes and occurrence
The occurrence of a tsunami can have several causes[1]. The main cause, responsible for the strongest tsunamis, are seaquakes (submarine earthquakes): the sudden uplift of the seabed due to shifting earth plates. This mainly occurs in subduction zones, where an earth plate slides under an adjacent earth plate causing vertical motion of the submarine crust along the subduction line. The most important subduction zones lie along the edges of the Pacific Ocean, the so-called ring of fire (see Fig. 1). The strength of the tsunami depends not only on the vertical and horizontal size of the seafloor uplift, but also on the speed at which the seafloor rises. The strongest response occurs when this speed is comparable to the local wave propagation speed. The tsunami wave radiates in both directions perpendicular to the subduction line.
A second important cause is submarine gravity mass wasting. Such slides can be triggered by seismic activity at a sloping seabed (e.g., the shelf break) that is covered with a thick layer of unconsolidated material. The tsunami wave propagates in the direction of the slide and is strongest if the speed of the debris flow is comparable to local wave propagation speed. Gas formation (methane) due to the anaerobic degradation of organic material can contribute to the loss of stability of the sediment layer on the sloping seabed [2]. Volcanic activity and subaerial landslides can also cause tsunamis, but these are usually not as strong. A tsunami can in rare cases result from the impact of a large meteorite.
Another type of tsunamis, so-called meteotsunamis, can arise from atmospheric disturbances. Sudden local pressure fluctuations can generate a small setup or set-down of the water level that is amplified if the atmospheric front propagates at a speed comparable to the wave propagation speed or if the spatial/temporal scales coincide [3]. The amplitude of meteotsunamis is usually small, but it can increase strongly due to resonance effects in semi-closed basins (e.g., harbor seiches, which are damaging for moored ships).
Tsunami characteristics
A tsunami usually consists of a number of waves (up to about ten) of different amplitude [4]. The third, fourth or fifth wave are often the highest [5]. The characteristic wave period is different for each tsunami, but usually much greater than the period of wind-driven waves (i.e., more than a few minutes) and much smaller than the tidal period (i.e., less than two hours). The wave height can be a few meters at the place of origin, but when the tsunami starts propagating over the ocean the wave height quickly becomes smaller and is then usually less than one meter[6]. The wavelength is much greater than the water depth and the energy loss during ocean propagation is small (approximately inversely proportional to the wavelength). The propagation speed [math]c[/math] can therefore be approximated with the formula [math]c = \sqrt {gD}[/math], where [math]D[/math] is the average depth and [math] g [/math] the gravitational acceleration. Tsunamis travel at great speed across the ocean ([math]c[/math] in the order of a few hundred m/s) covering distances of many thousands of kilometers without great energy loss. The energy flux [math] F [/math] can be estimated with the formula [math]F = cE \approx (1/8) \rho g H ^ 2 \sqrt {gD}[/math], where [math]E[/math] is the tsunami wave energy, [math] H [/math] the tsunami wave height and [math]\rho[/math] the water density. When the tsunami reaches the coastal zone, the water depth decreases sharply as does the propagation speed [math] c [/math]. However, frictional energy dissipation being relatively modest, the energy flux [math]F[/math] remains almost the same. This implies [math]H_{shore}/H_{ocean} \approx (D_{ocean}/D_{shore})^{1/4}[/math]: the wave height [math]H[/math] of the tsunami is strongly increased, up to about 5 times the wave height on the ocean. The wave height can be amplified even more in marine inlets, such as bays, fjords or harbours, where the tsunami energy flux is concentrated and accelerated due to strong funnel effects [1]. The tsunami waves are also distorted when entering shallow water; when the rear of the wave train is still traveling in deeper water it gets closer to the front of the wave train which is already travelling in shallow water. Differences in propagation speed of wave crest and wave trough contribute to steepening of the wave front on wide continental shelfs - wide compared to the tsunami wavelength.
When the tsunami wave arrives at the coast it runs up the shoreface (schematically depicted in Fig. 6). If the slope is steep (the width of the shoreface being much smaller than the wavelength of the tsunami, i.e. less than 10 km), the tsunami 'feels' the shoreface as a straight wall. The tsunami is then almost completely reflected and the wave height is doubled. The tsunami floods the coast as a surging wave with a relatively low speed that can be outrun. The wave run-up is not much higher than the wave height on the foreshore.
If the shoreface slope is gentle (the length of the foreshore being of the same order or greater than the wavelength), the tsunami transforms into an undular bore, with short waves riding on the main tsunami wave. When reaching the shore, the tsunami transforms further into a breaking bore (a wall of water, see Fig. 2) that propagates at great speed with a very fast rising water level. The wave run-up is much higher than the wave height at the toe of the shoreface (a factor of 2 and possibly more).
The above qualitative description suggests that the character of a tsunami is related to the surf similarity parameter [math]\xi[/math] [7][8][9],
[math]\xi = \Large\frac{S}{\sqrt{2 A_0/L_{\infty}}}\normalsize = \Large\frac{S}{\omega} \sqrt{\frac{\pi g}{A_0}}\normalsize , [/math]
where [math]A_0[/math] is the tsunami wave height above mean sea level at the toe of the shoreface slope, [math]L_{\infty} = g T^2/(2 \pi)[/math] is the tsunami wave length at infinite depth, [math]S[/math] is the shoreface slope and [math]\omega[/math] is the tsunami wave period. Surging waves correspond to high values of [math]\xi[/math] and breaking waves to low values.

A distinction is often made between two types of tsunamis: tsunamis where the largest wave crest precedes the largest wave trough (sometimes called leading-elevation N-wave or LEN-wave) and tsunamis where the largest wave crest is preceded by the largest wave trough (sometimes called leading-depression N-wave or LDN-wave). Both types of tsunami occur in practice. In case of a LDN-wave, the sea retreats over a large distance and part of the shoreface falls dry before arrival of the wave crest, see Fig. 3. This is an important signal for bathers that a high tsunami wave is approaching. A LDN-wave approaches the shore at a lower speed than a similar LEN-wave, but the runup speed on land is in both cases of the same order.
Tsunami impact
Tsunamis can cause enormous damage to coastal infrastructure, crushing houses, deracinating trees and making many casualties, see Fig. 4. From historical records it has been estimated that more than a million people have been killed worldwide by tsunamis [11]. In low-lying coastal areas (less than 10 m elevation above mean sea level) tsunamis can penetrate several kilometers inland. There are even records of tsunamis that have penetrated several tens of kilometers inland and have reached levels of several tens of meters. The flood water volume is approximately equal to the water volume above beach level of the incident tsunami wave [12]. Runup velocities of strong tsunamis are very high; velocities of the order of 5 – 8 m/s are common and speeds up to 20 m/s have even be observed[13]. The destructive power of tsunamis is largely due to the many debris that are dragged by the flow. Upon travelling inland the flow gradually slows down. The largest debris are deposited first whereas the finest sediments are transported further inland. Sedimentary records showing upward fining deposits over large distances are a distinctive mark of tsunami events. The return flow to the sea (backwash) can also be very strong and dangerous; it follows the strongest topographic slope and is often concentrated in channels, with velocities that are often higher than during the uprush [14].
Why are tsunamis so devastating
The period of tsunami waves is typically in the range 300 – 6000 s (angular frequency in the order of 0.001 – 0.02 [math]s^{-1}[/math]). Therefore, these waves are rather insensitive to the effect of earth's rotation, which corresponds to a frequency smaller than 0.00015 [math]s^{-1}[/math]. Tsunami waves in the ocean have wavelengths typically in the order of 100 to 500 km and on the continental shelf in the order of 1 – 10 km. This implies that they are refracted and diffracted by seabed structures with spatial scales of these orders of magnitude. More specifically, this means that tsunami waves refract to the continental shelf and approach the shore more or less perpendicularly. The energy flux of tsunami waves is thus directed toward the coast. This contrasts with tidal waves that are too long for being refracted to the coast. Due to their very low frequency, tidal waves are bent along the coast by the effect of earth's rotation (see Coriolis and tidal motion in shelf seas). The energy flux of tidal waves, which is comparable in strength to the energy flux of tsunami waves, is therefore not directed towards the coast, but along the coast. Hence, the impact of tidal waves on the coast is much less than the impact of tsunami waves. Just like tsunami waves, wind-generated waves are also refracted to the coast. Their energy density on the ocean is generally higher than the energy density of tsunami waves. However, the energy propagation speed of wind waves is much lower and so is the corresponding energy flux. Hence, wind waves are much less amplified when travelling into shallow water than tsunami waves. Moreover, wind waves lose a great deal of their energy due to breaking in the surf zone before they reach the shore. This explains why tsunamis have a far more devastating effect on the coast compared to tidal and wind waves.
Tsunami observation and warning
Experimental measurements of real-life tsunamis running up the coast do not exist. Installing observation equipment at specific locations in anticipation of a tsunami makes no sense. Tsunami's are very rare events for each specific coastal location, even in areas that are very sensitive to submarine earthquakes. Experimental information about tsunamis that actually occurred is based on the effects observed in the coastal area after being hit by a tsunami. In some cases, eyewitness reports or amateur films are available. Although very important, this is insufficient for gaining in-depth understanding of the hydrodynamic processes that occur when a tsunami hits the coast. For this reason, understanding tsunamis is primarily based on modelling, as described in the next section.
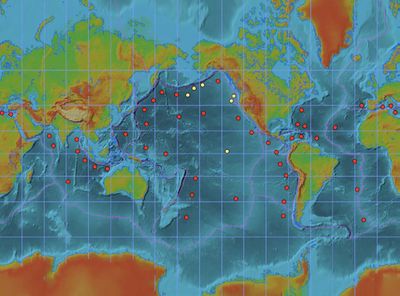
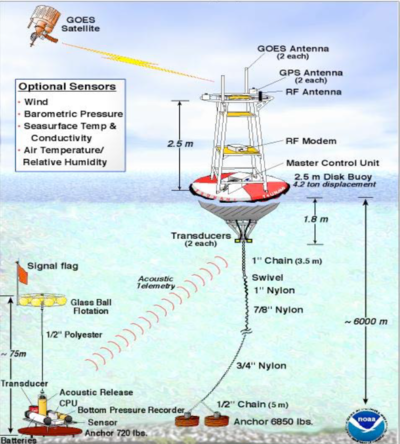
Tectonic activity that generates tsunamis is recorded by many seismic stations around the world. However, submarine earthquakes do not necessarily cause a tsunami. Tsunamis traveling across the ocean are very long waves of small amplitude that cannot be easily detected visually or by ships. For tsunami warning, an extensive network of monitoring stations has been installed in ocean areas where tsunamis can occur. The largest network is the DART system [15] consisting of an array of stations in the Pacific Ocean, see fig. 5a. Each station consists of a seabed pressure recorder that detects the passage of a tsunami. The data is sent by sonar signal to a moored buoy. This buoy sends a radio signal via satellite to the Pacific Tsunami Warning Center, see Fig. 5b. In this way, a tsunami traveling across the ocean can be detected and an early warning can be issued to countries where the tsunami will land, allowing timely evacuation of risk populations. The information collected by the monitoring network also enables to estimate the nature and intensity of the tsunami and the possible impact on the coast.
Tsunami models
Due to the lack of field observations, one has to rely on models for gaining insight into the hydrodynamic processes involved in tsunami events. The propagation of tsunami waves over the continental shelf and the shoreface can be simulated in hydraulic scale models based on Froude scaling, as long as boundary-layer processes are of minor importance. Scale effects occur when energy dissipation (wave breaking, bed friction) comes into play. This imposes a limitation on the simulation of the inland runup process in the laboratory. The same limitation applies to simple mathematical models that do not include wave breaking and friction. Detailed process-based numerical models are required for simulating these effects. A thorough model study of this type has been carried out by Larsen and Furman (2019)[8].
A major problem for predicting the impact of tsunamis lies in the fact that the initial tsunami-generating disturbance cannot be predicted and is generally not well known. When a tsunami wave is detected on the ocean, the time is too short for an accurate calculation of the impact before the tsunami lands on the coast. Only theoretical or semi-empirical relationships can be used.
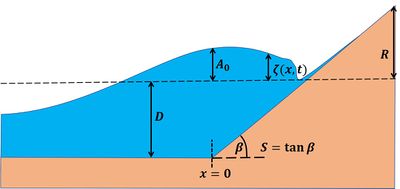
Relationships for the tsunami runup height and runup velocity, validated with laboratory experiments and advanced numerical models, are based on the theoretical work of Madsen and Schäfer (2010)[9]. They solved analytically the non-linear shallow-water equations (mass and momentum balance) over a sloping bed,
[math]\Large\frac{\partial \zeta}{\partial t}\normalsize + \Large\frac{\partial}{\partial x}\normalsize [(D+\zeta -Sx)u] = 0 , \quad \Large\frac{\partial u}{\partial t}\normalsize + u \Large\frac{\partial u}{\partial x}\normalsize + g \Large\frac{\partial \zeta}{\partial x}\normalsize =0 , [/math]
where [math]t[/math] is time, [math]x[/math] is the spatial coordinate in the propagation direction, [math]D[/math] is the average shelf depth, [math]S[/math] is the average shoreface and beach slope, [math]\zeta[/math] is the surface elevation and [math]u[/math] is the depth-averaged current velocity. The corresponding schematization is shown in Fig. 6. Madsen and Schäfer considered an incident tsunami wave of the form
[math]\zeta(0,t) = A_0 \cos(\omega t) .[/math]
For a non-breaking tsunami wave they arrived at the following expressions for the maximum runup height [math]R[/math] and the maximum runup velocity [math]V[/math]:
[math]R = 2 \pi^{3/4} A_0 (D / A_0)^{1/4} \xi^{-1/2} , \quad V = 2 \pi^{5/4} (A_0 / D) \sqrt{g A_0} \xi^{-3/2} . [/math]
These simple expressions represent fairly well detailed numerical model results that include wave breaking, bed friction and turbulent energy dissipation[8]. The numerical model gives somewhat higher values of [math]R[/math] and [math]V[/math], but in practice the values might be lower due to energy dissipation on obstacles that are generally present the runup area.
The numerical model [8] also provides results for [math]R[/math] and [math]V[/math] in the case of a breaking tsunami. These results are best approximated by
[math]R = A_0 \xi , \quad V = 2 \sqrt{g A_0} .[/math]
The first expression corresponds to the formula established by Hunt (1959) [16] for swash uprush (see the article Swash zone dynamics) and the second expression corresponds to the initial flow velocity after dam break (see the article Dam break flow).
Non-breaking tsunamis occur for large [math]\xi[/math]-values [math]\xi \gt \xi_b[/math], corresponding to a steep shoreface/beach slope and long-period tsunamis. Breaking tsunamis occur for small [math]\xi[/math]-values [math]\xi \lt \xi_b[/math], corresponding to gentle shoreface/beach slope and short-period tsunamis. According to the numerical model [8], [math]\xi_b \approx 3 (D / A_0)^{1/6}[/math].
The above relationships are the result of recent studies (up to 2019) of tsunami irruption on a coast. However, further underpinning of the above results is needed, given that previous investigations produce results that differ in some respects [7]. Synolakis [17] modeled the tsunami as a solitary wave of height [math]H[/math]. This model, which was validated with other laboratory measurements, yields for the runup height of a tsunami the relationship
[math]R = 2.8 H S (H/D)^{5/4} .[/math]
A purely empirical rule for the maximum runup of a tsunami was proposed by Plafker (1964, unpublised). This rule states that the maximum runup will not exceed twice the height of the seafloor deformation resulting from a submarine earthquake [10].
Related articles
References
- ↑ 1.0 1.1 Röbke, R.B. and Vött, A. 2017. The tsunami phenomenon. Progress in Oceanography 159: 296–322
- ↑ Tinivella, U., Accaino, F. and della Vedova, B. 2008. Gas hydrates and active mud volcanism on the south Shetland continental margin, Antarctic Peninsula. Geo-Mar. Lett. 28: 97–106
- ↑ Monserrat, S., Vilibić, I. and Rabinovich, A.B. 2006. Meteotsunamis: atmospherically induced destructive ocean waves in the tsunami frequency band. Nat. Hazards Earth Syst. Sci. 6: 1035–1051
- ↑ Grilli, S.T., Harris, J.C., Tajalli Bakhsh, T.S., Masterlark, T.L., Kyriakopoulos, C., Kirby, J.T. and Shi, F. 2013. Numerical simulation of the 2011 Tohoku tsunami based on a new transient FEM Co-seismic source: comparison to far- and near-field observations. Pure Appl. Geophys. 170: 1333–1359
- ↑ Murty, T.S. 1977. Seismic sea waves. Tsunamis. In: Stevenson, J.C. (Ed.), Bulletin of the Fisheries Research Board of Canada, vol. 198
- ↑ Bolt, B.A., Horn, W.L., Macdonald, G.A. and Scott, R.F. 1975. Geological hazards. Earthquakes—Tsunamis—Volcanoes—Avalanches—Landslides—Floods. Springer, New York
- ↑ 7.0 7.1 McGovern, D.J., Robinson, T., Chandler, I.D., Allsop, W. and Rossetto, T. 2018. Pneumatic long-wave generation of tsunami-length waveforms and their runup Coastal Engineering 138: 80–97
- ↑ 8.0 8.1 8.2 8.3 8.4 Larsen, B.E. and Fuhrman, D.R. 2019. Full-scale CFD simulation of tsunamis. Part 1: Model validation and run-up Coastal Engineering 151: 22–41
- ↑ 9.0 9.1 9.2 Madsen, P.A. and Schäffer, H.A. 2010. Analytical solutions for tsunami runup on a plane beach. J. Fluid Mech. 645: 27–57
- ↑ 10.0 10.1 Synolakis, C.E. and Bernard, E.N. 2006. Tsunami science before and beyond Boxing Day 2004. Phil. Trans. R. Soc. A. 364: 2231–2265
- ↑ National Geophysical Data Center/World Data Service, 2015. Global historical tsunami database. Tsunami event data. <http://www.ngdc.noaa.gov/hazard/tsu_db.shtml>
- ↑ Bryant, E.A., 2008. Tsunami: The Underrated Hazard, second ed. Springer, Berlin
- ↑ Nanayama, F. and Shigeno, K. 2006. Inflow and outflow facies from the 1993 tsunami in southwest Hokkaido. Sed. Geol. 187: 139–158
- ↑ Le Roux, J.P. and Vargas, G. 2005. Hydraulic behavior of tsunami backflows: insights from their modern and ancient deposits. Environ. Geol. 49: 65–75
- ↑ Deep-ocean Assessment and Reporting of Tsunamis, https://www.ndbc.noaa.gov/dart/dart.shtml
- ↑ Hunt, I.A. 1959. Design of seawalls and breakwaters. J. Waterw. Harbors Division ASCE 85: 123–152
- ↑ Synolakis, C. E. 1987. The runup of solitary waves. J. Fluid Mech. 185: 523–545