Talk:Beach Cusps
A more quantitative explanation of the self-organizing beach cusp mechanism was given by Dean and Maurmeyer, as given below.
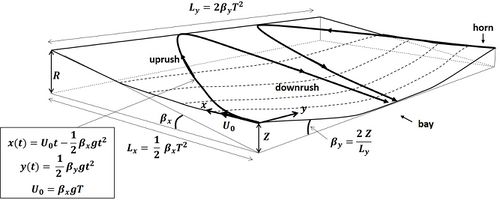
The scouring of incipient beach cusp embayments is due to the diversion of the wave uprush (swash excursion) from the incipient horns to the incipient embayments where consequently the wave downrush velocity is greater than the uprush. The inverse (minimum downrush) holds for the incipient horns that therefore will accrete. The Dean-Maurmeyer model is based on the assumption: The cusp planform that will develop after an initial perturbation will correspond to the situation where the embayment wave downrush is maximum.
The proportion of uprush that is diverted from the incipient horns to the incipient embayments is maximum when the swash diversion (uprush and downrush) equals half the embayment width, i.e. half the beach cusp spacing [math]L_y[/math], see Fig. 1. Half the maximum diversion occurs at time [math]T[/math] when the uprush has reached its highest point. In the simplest model of frictionless particle motion over a slope, the time [math]T[/math] depends on the ratio of distance to slope, for both the cross-shore and longshore directions. The maximum downrush in the embayment thus corresponds to the situation where the ratio longshore uprush diversion [math]L_y / 4[/math] to longshore slope [math]\beta_y[/math] equals the ratio cross-shore uprush [math]L_x[/math] to cross-shore slope [math]\beta_x[/math]. The beach cusp spacing [math]L_y[/math] is four times the longshore uprush diversion, thus proportional to [math]\beta_y L_x / \beta_x[/math]. The longshore slope [math]\beta_y[/math] is inversely proportional to the beach cusp spacing [math]L_y[/math] and proportional to the elevation difference [math]Z[/math] between horn and valley. This yields the formula [math]L_y \propto \beta_y L_x / \beta_x \propto Z L_x / (L_y \beta_x) [/math]. The elevation difference [math]Z[/math] cannot be larger than the vertical uprush (wave run-up) [math]R = \beta_x L_x[/math] and will become a certain proportion of [math]R[/math] in the course of cusp development. Substitution gives [math]L_y \propto Z L_x / (L_y \beta_x) \propto R L_x / (L_y \beta_x) \propto L_x^2 / L_y[/math] which implies [math]L_y \propto L_x[/math]. Maximum scouring of the embayment thus occurs when the cusp spacing [math]L_y[/math] is proportional to the wave uprush [math]L_x[/math].
The above model is of course an oversimplification of the beach cusp development process. It does not take into account many factors that can have a significant influence, such as frictional momentum dissipation, oblique and varying wave incidence angles, infragravity waves, etc. However, the basic assumption that beach cusps develop by maximizing the scouring downrush in an incipient embayment along the shoreline is highly plausible and yields a result that is close to what is observed in the field.
Reference:
Dean, R.G. and Maurmeyer, E.M. 1980. Beach cusps at Point Reyes and Drakes Bay, California. In: Procs. Int. Conf. Coastal Eng. ASCE, New York, 863-884.