Wavelet analysis of coastal processes

Introduction

Fourier analysis provides information on the frequency content of a signal by decomposing a signal into sinusoidal components. When the dominant processes have a linear or weakly nonlinear and approximately periodic character, the signal can often be represented accurately by a limited number of sinusoidal components. However, an accurate Fourier representation may require many components for signals without fixed periodicity or with localized features.

Wavelet analysis provides an alternative representation by decomposing the signal into functions that are localized in time or space and have different characteristic scales. It is therefore particularly suitable for representing transient and localized features and signals without fixed periodicity, while retaining a decomposition according to scale. A relatively small number of wavelet components may then provide an accurate representation of signals that would require many sinusoidal components in a Fourier representation (Burrus et al., 1998). An important property of wavelets is that their mean is zero; they are generally normalized to have unit squared norm.

Well-known examples of wavelets are the Mexican hat and the Morlet wavelet, see Fig. A1 of the appendix. These are examples of mother wavelets, which may be dilated and translated to form the wavelet basis. The first wavelet function was developed by Haar (1910). Wavelets have traditionally been used in data analysis to increase the signal-to-noise ratio, and also to compress the data to only a few wavelet functions.

Two main forms of wavelet analysis are commonly distinguished. The continuous wavelet transform (CWT) provides a detailed representation of how the spectral content of a signal varies with time (or space). Discrete wavelet transforms (DWT) decompose a signal into a finite set of components representing different scale ranges and are particularly useful for multiresolution analysis, filtering and data compression. Wavelets achieve resolution in time (or space) because each wavelet is localized: it is a window of limited length, scaled to the frequency band considered, that is shifted along the signal. In the continuous wavelet transform the window is shifted continuously. In the discrete wavelet transform it is shifted in steps that increase with scale, so that at large scales the position of a feature is resolved only coarsely and the result depends on where the record starts. The maximal overlap discrete wavelet transform (MODWT) avoids this by computing the wavelet coefficients at every sample position; see the Appendix.

Application in coastal bathymetry studies

An early application of wavelets to seabed topography by Sarah Little et al. (1993) was the analysis of large scale (of the order of 100 to 1000 km) bathymetric structure northeast of Hawaii; the wavelets the authors adopted for this analysis were Daubechies wavelets (see Appendix), a family of discrete orthogonal wavelets introduced by Ingrid Daubechies (1988). Based on scale analysis by applying a wavelet transform, the authors were able to discover a 200 km long low-frequency topographic zone, interpreted as a small abandoned slow-spreading rift. After this pioneering work, other topography identification investigations followed (eg. Little et al., 1996).

In a first coastal application, Li et al. (2005) analyzed nearshore beach profile variability at the Duck study site, North Carolina (USA). The space scales in this case were, instead, of the order of 0.1 km. The objective of the study was to analyze both time and space variability of the bathymetry. The authors also chose Daubechies’ wavelets as a base and an adapted maximum overlap discrete wavelet transform (AMODWT), as both are very suitable for decomposition of signals with strong space and time variations. Data of the bathymetry profile were available from thorough surveys since 1981. The analysis showed that beach-profile variability was strongly dependent on both location and scale. The largest spatial variability occurred in the sandbar region. The temporal variability differed with position along the profile. The wavelet decomposition revealed localized patterns of morphological variability that would be obscured in an analysis based only on the variance of the complete profile record.

Application in storm wave studies

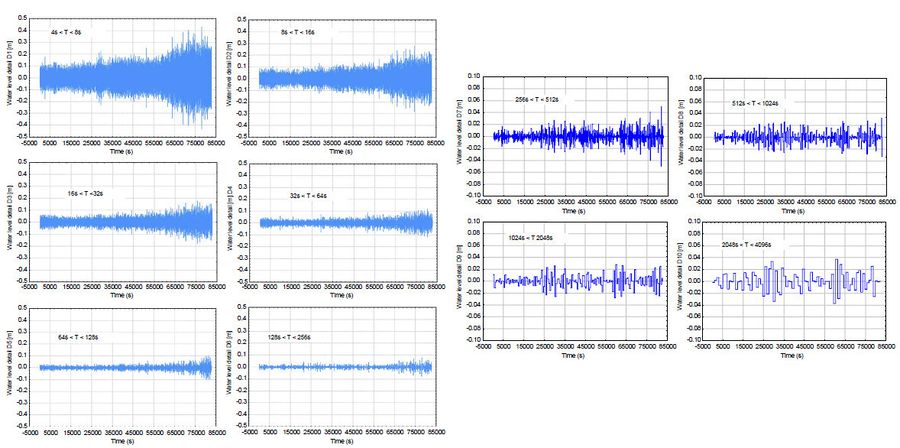
An example how a signal can be decomposed into different spectral bands using orthogonal wavelets was given by Różyński and Reeve (2005). Water levels were measured at a Baltic Sea coastal segment in Poland during a stormy event on 27th Oct. 2002, sampled at the rate of 0.5 Hz. Fig. 1, left panel, presents the results of wavelet decomposition with the orthogonal Haar wavelet (see Appendix) for frequency bands covering wind waves (4 – 8 s), swell (8-16 s) and infragravity waves (16-256 s). The growth of wave height of all those components during the storm buildup can clearly be seen.

Figure 1. Left panel: Spectral bands with water wave components. Right panel: Spectral bands with residual slow-varying components.

Figure 2: So-called 'smooth representation' of water level by Haar wavelets.

Fig. 1, right panel, shows residual spectral bands, which are roughly the same throughout the storm. The patterns belonging to each spectral band are called ‘details’ in wavelet terminology, whereas the pattern in Fig. 2 contains elements with periods above 4096 s i.e. the ultra-slow varying trend, featuring the storm surge. This pattern is called ‘smooth representation’ in wavelet terminology. We can see that the storm was decomposed into spectrally orthogonal, partially overlapping patterns, allowing for their detailed, individual examination; in wavelet terminology the smooth representation and details together are all parts of multi-resolution analysis of a time series. Jagged trajectories of the smooth representation and details describing long-period variability originate from the step shape of the Haar wavelet transform. More advanced Daubechies wavelets reduce such artefacts.

A Fourier spectrum could identify the spectral bands present during the storm, but would not directly show how growth of the amplitudes of these components evolved during storm build-up. The wavelet decomposition retains this temporal information.

Appendix A: Introduction to wavelet theory

Continuous Wavelet Transforms (CWT)

Continuous wavelets make it possible to analyze characteristic patterns of signals [math]y(t)[/math] in both the time (or space) domain and the frequency domain. The word 'signal' denotes the outcome of a process; we consider signals of limited length and assume that they are sampled at intervals much smaller than the signal length. The samples form a data record of [math]N[/math] numbers that can be analyzed by numerical methods. In the following, the words signal and data record are sometimes used indiscriminately.

Wavelet analysis is often used in cases where the frequency spectrum of a signal changes with time (or space); examples are data records representing bathymetry, wave registrations and many other common phenomena such as audio recordings. Fourier analysis of a signal [math]y(t) \rightarrow \hat{y}(f) = \int_{-\infty}^{\infty} \, y(t) \, e^{-2 i \pi f t} dt[/math] provides information only on the overall frequency content of the signal. When the frequency spectrum changes significantly along the signal, Fourier analysis requires dividing the signal into separate time (or space) slices. However, since the number of data points in each slice is similar, information about low frequencies is lost, while information about high frequencies may be redundant. Unlike Fourier transforms, wavelets have a time (or space) window that is moved along the signal and has a length that is adapted to each frequency domain studied. They are suitable not only for signal characterization, but also for signal compression.

Fig. A1. The mother wavelet functions of Morlet and Ricker (also called 'Mexican hat').

Different types of wavelet functions [math]\psi(t)[/math] can be used; a few examples are shown in Fig. A1. The functions [math]\psi(t)[/math] in these examples are so-called 'mother wavelets' which probe a frequency domain around a reference frequency [math]\nu[/math] often taken as 1 Hz and a time window around [math]t=0[/math]. In the following, we use dimensionless time [math]t^*=\nu \, t[/math] and dimensionless frequency [math]f^*=f/\nu[/math]. The mother wavelets are generalized by adapting the frequency domain and the time origin,

[math]\psi(t^*) \longrightarrow \psi_{f_0^*,t_0^*}(t^*) \equiv \psi\big(f_0^*(t^*-t_0^*)\big) , \qquad (A1)[/math]

The continuous wavelet transform [math]T(f_0^*,t_0^*)[/math] is the projection of the signal [math]y(t^*)[/math] on the wavelet component [math]\psi_{f_0^*,t_0^*}[/math] for different frequencies [math]f_0^*[/math] and time origins [math]t_0^*[/math]. For convenience of writing we drop the [math]^*[/math] from [math]t[/math] and [math]f[/math] in the rest of this section.

The wavelet function acts as a filter on the signal:

[math]T(f_0,t_0)=\sqrt{f_0} \, \int_{-\infty}^{\infty} \, dt \, y(t) \, \psi^*\big(f_0(t-t_0)\big) . \qquad (A2)[/math]

The integration extends over the whole signal length; the integration limits can be set to [math]\pm \infty[/math] because the wavelet function is practically zero for large [math]|t|[/math]. The symbol [math]\psi^*[/math] stands for the complex conjugate of [math]\psi[/math] when the wavelet is represented by a complex function. For a complex wavelet such as Morlet, [math]|T(f_0,t_0)|[/math] provides a measure of the local strength of the signal component at frequencies around [math]f_c f_0[/math], while [math]\arg T(f_0,t_0)[/math] provides information on its phase. Here [math]f_c[/math] is a fixed constant, usually taken close to 1. Large values of [math]|T(f_0,t_0)|[/math] are indicative of time windows around [math]t_0[/math] where the dominant frequencies in the time series are close to [math]f_c f_0[/math].

Although the wavelet family [math]\psi_{f_0,t_0}(t)[/math] does not constitute an orthogonal basis, it is nevertheless possible to reconstruct the original time series from the transforms [math]T(f_0,t_0)[/math]. By using Fourier transforms it can be shown that

[math]y(t)=\Large\frac{1}{C}\normalsize \, \int_{-\infty}^{\infty} \, dt_0 \, \int_{0}^{\infty} \, df_0 \, \sqrt{f_0} \, \psi\big(f_0(t-t_0)\big) \, T(f_0,t_0), \quad C = \int_0^{\infty} \, \Large\frac{df}{f}\normalsize \, |\hat{\psi}(f)|^2 , \quad \hat{\psi}(f) = \int_{-\infty}^{\infty} \, \psi(t) e^{-2 i \pi f t} dt , \qquad (A3)[/math]

where it is assumed that [math]\hat{\psi}(0)=0[/math]. For a complex wavelet whose spectrum contains essentially only positive frequencies (such as the Morlet wavelet), the right-hand side of (A3) must be replaced by twice the real part.

Wavelet analysis of datasets is often carried out with the Morlet wavelet function (Fig. A1)

[math]\psi(t) = \large \big(e^{2 i \pi f_c t} - e^{-\tfrac12 (2 \pi f_c)^2 } \big) e^{ -\tfrac12 t^2} \normalsize . \qquad (A4)[/math]

For [math]f_c=1[/math] the Morlet mother wavelet probes frequencies around the reference frequency [math]\nu[/math]. The wavelet [math]\psi \big(f_0(t - t_0)\big) [/math] then responds mainly to frequencies close to [math]f_c f_0[/math].

The Fourier transform of this complex wavelet function (A4) is focused around [math]f=f_c[/math] and has essentially only positive frequencies,

[math]\hat{\psi}(f) = \sqrt{2 \pi} \Big[ \large e^{- 2 \pi^2 ( f - f_c)^2} - e^{- 2 \pi^2 (f^2 + f_c^2)}\normalsize \Big]. \qquad (A5)[/math]

Boundary effects
Because the available data record has finite length, wavelets centered near its boundaries partly extend beyond the observations. Wavelet coefficients near the beginning and end of the record are therefore affected by the assumed treatment of the boundaries, especially at low frequencies [math]f_0[/math]. For the Morlet wavelet in this notation, the edge zone extends roughly [math]\sqrt{2}/f_0[/math] from each end of the record, so it widens as [math]f_0[/math] decreases. In continuous wavelet analysis the region in which such edge effects become important is commonly indicated by a cone of influence.

The review by Addison (2018) gives more detailed information on continuous wavelet transforms.

Discrete Wavelet Transforms (DWT)

The continuous wavelet transform still contains considerable redundant information on the analyzed dataset and takes much computation time. Discrete wavelet transforms do not have these disadvantages and are often used for reduction of datasets that otherwise require large storage space. They are often used for image processing or for the compression of audio records.

The Haar wavelets

Fig. A2. Haar wavelets.

An example of a discrete wavelet is the Haar wavelet:

[math]H(t) = 1 , \; 0 \le t \lt \tfrac12 ; \;\; H(t) = -1 , \; \tfrac12 \lt t \le 1 ; \; \; H(t) = 0 , \; t \lt 0, \; t \gt 1 \qquad (A6) [/math]

We consider here a signal [math]y(t)[/math] covering the interval [math]0 \le t \le 1[/math], sampled at [math]N=2^{n+1}[/math] equidistant times [math]t_i[/math]. From the Haar wavelet (the 'mother' wavelet) we construct the wavelet family (see Fig. A2)

[math]\psi_{j,k}(t) = 2^{j/2} \, H(2^j \, t - k) , \; \; j=0, 1, .., n ; \; k = 0 , .., 2^j - 1 . \qquad (A7)[/math]

Together with the constant scaling function [math]\phi(t)=1[/math], these wavelets form a complete orthonormal basis on the interval [math]0\lt t\lt 1[/math],

[math] \lt \psi_{j,k}(t)\, \psi_{lm}(t)\gt = \int_0^1 \psi_{j,k}(t) \, \psi_{l,m}(t) \, dt = \delta_{j,l} \, \delta_{k,m} , \qquad (A8)[/math]

where [math]\delta_{j,j}=1, \; \delta_{j,l}=0, \; j \ne l[/math].

It can be shown that every continuous function [math]y(t)[/math] in the interval [math]0 \le t \le 1[/math] can be decomposed in a series of Haar wavelets with components [math]y_{j,k}=\lt y(t)\, \psi_{j,k}(t)\gt [/math],

[math]y(t) \rightarrow \lt y(t)\gt + \sum_{j=0}^n \, \sum_{k=0}^{2^j-1} \, y_{j,k} \, \psi_{j,k}(t) , \; n \rightarrow \infty . \qquad (A9)[/math]

The Haar wavelets can be thought of as filters that extract information from the signal [math]y(t)[/math] at successive levels of detail. The lowest level of detail is obtained by taking the average; this corresponds to projecting the signal [math]y(t)[/math] on the scale wavelet (also called 'father wavelet') [math]\phi(t) = 1, \; 0 \le t \le 1; \; \phi(t)=0[/math] elsewhere. The next levels of detail are obtained by applying the filters [math]\psi_{0,0}[/math], [math]\psi_{1,0}, \, \psi_{1,1}[/math], etc. The filters [math]\psi_{n,0}, \, \psi_{n,1}, …, \psi_{n,2^n-1}[/math] give the highest level of detail.

The step functions make the Haar wavelets computationally fast and easy to implement, but limit the ability of Haar wavelets to represent smooth functions. For that reason, other discrete wavelets have been developed.

The Daubechies wavelets

Fig. A3. The Daubechies scaling function [math]\phi(t)[/math] and mother wavelet function [math]\psi(t)[/math] of order [math]N_D[/math]=20. From Wikipedia.

The most popular alternative to the Haar wavelets are the Daubechies wavelets, which can be considered a generalization of the Haar wavelets. The Daubechies wavelet family, named after the Belgian mathematician Ingrid Daubechies, is smoother and forms an orthonormal basis. There is no explicit expression for the Daubechies wavelets; they are constructed iteratively by a recursive method. The mother wavelet [math]\psi(t)[/math] is constructed as a sum of the scaling functions [math]\phi(t)[/math], which satisfy

[math]\phi(t)= \sum_{k=0}^{N_D -1} a_k \, \phi(2t-k), \quad \lt \phi(t)\gt \equiv \int_{-\infty}^{\infty} \phi(t) \, dt = 1 \; \longrightarrow \; \sum_{k=0}^{N_D -1} a_k = 2 , \qquad (A10)[/math]

and orthonormality conditions

[math]\lt \phi(t)\, \phi(t+m)\gt \equiv \int_{-\infty}^{\infty} \phi(t) \, \phi(t+m) \, dt = \delta_{0,m} \; \longrightarrow \; \sum_{k=0}^{N_D -1} a_k \, a_{k+2m} = 2 \delta_{0,m} , \qquad (A11)[/math]

where the even number [math]N_D[/math] is the order to which the system is determined. The Daubechies mother wavelet is defined by

[math]\psi(t) = \sum_{k=0}^{N_D-1} (-1)^k a_{N_D-1-k} \, \phi(2t-k) . \qquad (A12)[/math]

It is orthogonal to the scaling function [math]\phi(t)[/math] because

[math]\sum_{k=0}^{N_D -1} (-1)^k a_{N_D -1-k} a_k = 0 \, . \quad (A13)[/math]

A distinctive feature of Daubechies wavelets is that they have [math]N_D/2[/math] vanishing moments, while the associated scaling functions can reproduce polynomials of degree up to [math]N_D/2-1[/math]. This yields the condition

[math]\sum_{k=0}^{N_D-1} (-1)^k k^m a_k = 0, \; \; m=0, .., N_D/2-1 , \qquad (A14)[/math]

which can be derived by expanding [math]t^m[/math] as [math]t^m = \sum_{k=-\infty}^{\infty} c_k \, \phi(t-k)[/math], where the coefficients [math]c_k[/math] are a polynomial of degree [math]m[/math] in [math]k[/math] (for example, [math]\sum_k \phi(t-k)=1[/math] for [math]m=0[/math]), and noting that [math]\lt \phi(t-k) \, \psi(t)\gt = 0[/math] for all integers [math]k[/math] and [math]\psi(t)=0[/math] outside the interval [math][0, N_D − 1][/math].

The coefficients [math]a_k[/math] are determined by the conditions (A10), (A11) and (A14) up to a reversal of their order ([math]a_k \rightarrow a_{N_D−1−k}[/math]) if [math]N_D\lt 8[/math] ; for larger values of [math]N_D[/math] several essentially different solutions exist.

The functions [math]\phi(t)[/math] can be constructed by sampling at integer values [math]t=1, t=2[/math], etc. and noting that [math]\phi(t)=0, \; t \lt 0; \; t \gt N_D-1[/math]. Using the condition (A10), the Daubechies scaling function [math]\phi(t)[/math] and mother wavelet [math]\psi[/math] can be determined by iteration to the desired accuracy. The order [math]N_D[/math] determines the smoothness, number of vanishing moments and spatial extent of the wavelet functions, and is chosen according to the characteristics of the signal and the purpose of the analysis. The scaling function and mother wavelet function of order [math]N_D=20[/math] are shown in Fig. A3. The wavelet family is derived from the mother wavelet in the same way as for the Haar wavelet and forms an orthonormal basis:

[math]\psi_{j,k} (t) = 2^{j/2} \, \psi^w (2^j t -k) , \quad \lt \psi_{j,k} (t) \, \psi_{l,m} (t) \gt = \delta_{j,l} \, \delta_{k,m} , \qquad (A15)[/math]

where [math]\psi^w (2^j t -k)[/math] is the rescaled wavelet function, wrapped to the unit interval [math][0,1][/math] and [math] \lt ..\gt [/math] stands for integration over this unit interval.

We consider again a signal [math]y(t)[/math] covering the interval [math]0 \le t \le 1[/math], sampled at [math]N=2^{n+1}[/math] equidistant times [math]t_i[/math]. For large [math]N_D[/math], the signal can be written as a superposition of Daubechies wavelets,

[math]y(t) = \lt y(t)\gt + \sum_{j=0}^{n} \sum_{k=0}^{2^j -1} c_{j,k} \, \psi_{j,k}(t) , \quad c_{j,k} = \lt y(t) \, \psi_{j,k}(t) \gt \, , \qquad (A16)[/math]

It can be easily checked that the Daubechies wavelets and Haar wavelets become identical when choosing [math]N_D=2, \; a_0=a_1=1[/math].

The reviews by Williams and Amaratunga (1994) and Rowe and Abbott (1995) give more detailed information on discrete wavelet transforms.

The maximal overlap discrete wavelet transform (MODWT)

The discrete wavelet transform described above has two practical drawbacks. First, the dyadic DWT decomposition described above assumes a data record of length [math]N=2^{n+1}[/math]. Second, at detail level [math]j[/math] it produces only one coefficient for every [math]2^{n+1-j}[/math] samples (the wavelets [math]\psi_{j,k}[/math] are shifted in steps of [math]2^{-j}[/math], not sample by sample). As a consequence, the result depends on where the record happens to start: shifting the record by one sample can change the wavelet coefficients completely. The maximal overlap discrete wavelet transform (MODWT) removes both drawbacks by computing the wavelet coefficients at every sample position. MODWT is an extension of DWT obtained by computing the filter outputs at every sample instead of every [math]2^j[/math]-th sample, with filters rescaled by a factor [math]1/\sqrt{2}[/math] per level. It can be used to construct a multiresolution decomposition in which the smooth and detail components are defined at every sample position. The following formulation directly computes these components using symmetric filters derived from the Daubechies scaling coefficients.

Consider a data record [math]y_i, \; i=0, .., N-1[/math] of arbitrary length [math]N[/math]. We define the 'smooths' [math]S_{j,i}[/math], which are the part of the signal with periods longer than about [math]2^{j+1}[/math] sampling intervals. Starting from [math]S_{0,i}=y_i[/math], they are determined by iteration from the relation

[math]S_{j,i} = \sum_{n=-(N_D-1)}^{N_D-1} c_n \, S_{j-1,i+2^{j-1}n} , \quad c_n = c_{-n} = \tfrac14 \sum_k a_k \, a_{k+n} , \quad S_{0,i} = y_i . \qquad (A17)[/math]

Near the ends of the record, (A17) requires values outside the record; the record is then usually extended periodically or by reflection, and the first and last [math](2^j-1)(N_D-1)[/math] values at level [math]j[/math] are affected by this choice.

Because of (A11), [math]c_0 = \tfrac12[/math] and [math]c_n = 0[/math] for even [math]n \ne 0[/math]. For the Haar wavelet, [math]S_{j,i} = \tfrac14 S_{j-1,i-2^{j-1}} + \tfrac12 S_{j-1,i} + \tfrac14 S_{j-1,i+2^{j-1}}[/math]. The 'detail' [math]D_{j,i}[/math] at level [math]j[/math] is the difference between two successive smooths,

[math]D_{j,i} = S_{j-1,i} - S_{j,i} , \qquad (A18)[/math]

and contains the components with periods between about [math]2^j[/math] and [math]2^{j+1}[/math] sampling intervals. Note that MODWT level [math]j[/math] corresponds to DWT level [math]n+1-j[/math]; in MODWT, smaller [math]j[/math] yields finer local detail. Summation over all levels gives the exact decomposition

[math]y_i = \sum_{j=1}^J D_{j,i} + S_{J,i} . \qquad (A19)[/math]

Each detail [math]D_{j,i}[/math] and the smooth [math]S_{J,i}[/math] are aligned in time (or space) with the original record, so that features in the different scale bands can be compared directly with events in the signal, such as a storm.

For the Haar wavelet (corresponding to [math]N_D=2, \; a_0=a_1=1[/math]), level 1 is given by [math]S_{1,i} = \tfrac14 y_{i-1} + \tfrac12 y_i + \tfrac14 y_{i+1}[/math] and [math]D_{1,i} = -\tfrac14 y_{i-1} + \tfrac12 y_i - \tfrac14 y_{i+1}[/math]. Figs. 1 and 2 show such a multi-resolution analysis: details and a smooth that add up to the original signal.

A detailed treatment of the MODWT is given by Percival and Walden (2000).

Related articles

Data analysis techniques for the coastal zone

Linear regression analysis of coastal data

Analysis of coastal processes with Empirical Orthogonal Functions

Artificial Neural Networks and coastal applications

Data interpolation with Kriging

Random Forest Regression

Support Vector Regression

References

The main authors of this article are Grzegorz, Rozynski, Job Dronkers, Vanessa, Magar and James, Sutherland Please note that others may also have edited the contents of this article. For other articles by this author see Category:Articles by Grzegorz, Rozynski For other articles by this author see Category:Articles by Job Dronkers For other articles by this author see Category:Articles by Vanessa, Magar For other articles by this author see Category:Articles by James, Sutherland