Flocculation cohesive sediments
Because the information on flocculation of cohesive sediments is dispersed over several articles, the most relevant sections are brought together here. They are imported from the articles Dynamics of mud transport, Sediment deposition and erosion processes and Coastal and marine sediments.
Contents
Flocculation of cohesive sediments
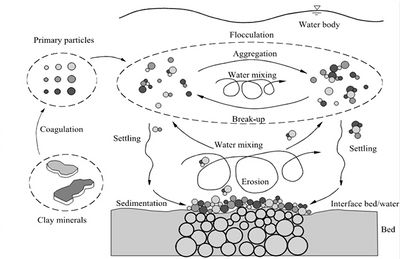
A key feature of mud particles is their cohesive nature that distinguishes them from non-cohesive solid particles such as sand. In soil, only clay minerals possess electrochemical cohesion. The median diameter of the size distribution of clay minerals is typically in the range of 1-2 μm and the spread is about 0.1 to 10 μm. Since clay minerals have a large surface area relative to their weight, the electrical surface charges ensure that they easily bind to one another (coagulate) and to other substances in an aquatic environment as the result of the Van der Waals forces. This process is enhanced by slimes (EPS) and mucus produced by micro-benthos and bacteria (that feed on decaying organic matter). Clays are therefore classified as cohesive sediments. Mud floc dynamics are schematically illustrated in Fig. 1.
The mean threshold diameter (grainsize) [math]d_T[/math] of about 10 μm distinguishing the fractions cohesive particles and larger cohesionless particles has been deduced from the experiments of Migniot[2] on the settling of twenty-seven fine-grained sediments (natural and clay minerals) and a compilation of data by McCave et al.[3] on the erosion of beds of kaolinite flocs and fine-grained quartz (< 62.5 μm) particles.
The size, structure and density of flocs are determined by the forces experienced by the aggregate-particles. These forces comprise: hydrodynamic forces (especially shear), collisions between particles and electrochemical forces (determined by the composition of solid particles and dissolved ions in the ambient water). The latter explains also why mud particles in fresh and saline water have a different structure.
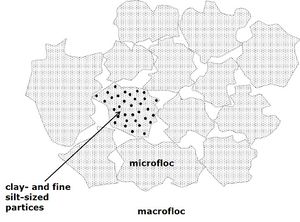
Flocs contain multiple mineral particles of generally much smaller diameters (van Olphen[4]), Fig. 2. They are watery with buoyant weights much lower than that of the mineral, which typically has a wet bulk density in the vicinity of 2,650 kg m-3. Flocs of silt size (less than about 100 [math]\mu[/math]m) are notionally called microflocs and those larger macroflocs (e.g. Eisma[5]). Natural flocs almost always contain organic detritus in variable proportions from practically nil to 100% by weight. Organic-rich mega-flocs (typically 1000 [math]\mu[/math]m) are often linked to seasonal biological events, such as algae-bloom). Their light weight and the biochemical bonding they provide can substantially influence floc properties (e.g. Gerbersdorf et al.[6]). Instead of microflocs, the term aggregates is also used, while the term flocs designates macroflocs (Law et al.[7]). Microflocs (aggregates) typically have undergone frequent cycles of formation, breakup, deposition and suspension during which inter-particle strength has increased presumably as a result of compaction and/or bacterial activity. The settling velocity of microflocs is usually greater than macroflocs of equal size due to their higher density and tighter packaging. Macroflocs (flocs) are associations of fine particles including microflocs that have recently formed, typically on tidal time scales. They have a loose structure and low density which makes them more susceptible to break up under turbulent stress. The simultaneous occurrence of micro- and macro-flocs is attributed to the tidal dynamics, and/or sometimes to the mixing of sea- and river-born aggregates.
Despite the trend to characterize the floc structure by a fractal number (Kranenburg[8]), the structure is not self-similar. In general, the fractal dimension decreases with increasing floc size, which implies that the floc structure becomes more and more open and its strength decreases.
The flocculation process and modelling are described in more detail in the Annex.
Settling Velocity
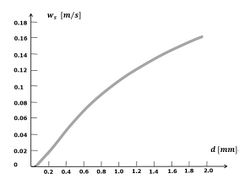
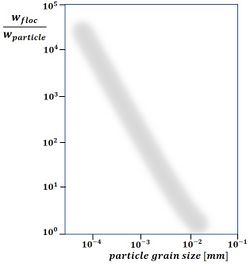
If the settling rate for very small particles, such as clay minerals, followed the curve for the settling rate of quartz spheres (see Figure 3), it would be so low that they almost never reach the bottom from suspension. The ubiquitous mud beds in coastal waters point to a different settling mechanism. This mechanism consists of flocculation, which incorporates these very small particles in flocs of much larger size and with aerodynamic shape. Observations show that flocs settle much faster than the individual constituent particles - a factor of a thousand or more, see Fig. 4. A substance that serves as a powerful binder is so-called EPS, extracellular polymeric substances (Grabowski et al.[9]). These large organic molecules (polysaccharides, proteins, nucleic acids and lipids) are exuded by living organisms and therefore omnipresent in coastal waters. Flocs grow much faster in natural seawater than in salinized distilled water (Skinnebach et al.[10]). In addition to EPS, bacterial colonization also plays a role in flocculation (Linley and Field[11]). Flocculation is further influenced by factors such as salinity and pH of the water. When flocs grow, they not only capture smaller flocs that settle more slowly, but also other suspended sediments, such as detritus, silt and fine sand. Frequent encounters between sediment particles are important for floc growth. Flocculation is thus enhanced with a high concentration of suspended material and with a certain (low) degree of turbulence (often expressed as the turbulent shear rate [math]G[/math]), dependent on the suspended sediment concentration (Mietta et al.[12]).
The process of flocculation occurs most often in a tidally dominated system during slack water, when the coincidence of elevated concentration and low-to-moderate turbulence allows flocs to grow. The time scale for floc formation depends on concentration squared (Hill et al.[13]). At high concentration, flocs form rapidly and settling begins almost immediately, but at low concentration there is a time lag before settling while particles form flocs. Disaggregation is the process of floc destruction and occurs under energetic conditions; marine aggregates or flocs break up when turbulent stress is at or above 0.1 Pa (the general case in estuaries)[13]. Deposition occurs when stress is low enough for flocs to settle from the water column. It is associated with decreases in concentration and overall particle size. As a suspension settles, however, a temporary increase in concentration near the seabed can occur[7].
Settling velocity formulas
Van Leussen[14] and others introduced the following expression for the settling velocity [math]w_s[/math]:
[math]{{w}_{s}}={{w}_{sh}}(G) \Large {{\left( \frac{\phi }{{{\phi }_{h}}} \right)}^{n}} \normalsize ;\quad {{w}_{sh}}(G)={{a}_{0}} \Large \left( \frac{1+{{\lambda }_{a}}G}{1+{{\lambda }_{b}}{{G}^{2}}} \right) \normalsize ;\quad \Large \frac{\phi }{{{\phi }_{h}}} \normalsize \le 1 , \qquad (1)[/math]
where the turbulent velocity shear rate [math]G[/math] is given by [math] G = \sqrt {\epsilon / \nu }=\sqrt{\Large\frac{\tau}{\rho \nu}\frac{dU}{dz}\normalsize} . \qquad (2)[/math]
Other symbols designate: [math]\phi =[/math] the volume fraction of cohesive sediment, [math]\epsilon =[/math] the energy dissipation rate per unit mass, [math]\tau =[/math] the shear stress, [math]\nu =[/math] the kinematic viscosity, [math]U(z) =[/math] the current velocity as a function of depth [math]z[/math]. The volume fraction at the onset of hindered settling is [math]\phi_h[/math] and [math]w_{sh}(G)[/math] is the maximum settling velocity for this volume fraction. The constants [math]a_0,\; n,\; \lambda_a, \; \lambda_b[/math] are independent of [math]G[/math] but depend, inter alia, on local sediment characteristics and must be determined experimentally. This expression is valid in the range [math]\phi \le \phi_h[/math]. The lowest applicable value of [math]\phi[/math] can be conveniently selected to correspond to the lowest experimental concentration [math]C[/math] of suspended sediment.
Setting [math]G = 0[/math] yields [math]\quad {{w}_{s}}={{w}_{sh}} \Large{{\left( \frac{\phi }{{{\phi }_{h}}} \right)}^{n}} \normalsize . \qquad (3)[/math]
A similar formula was derived empirically by Krone[16] with values of [math]w_{sh}[/math] and [math]n[/math] independent of [math]G[/math] deduced from settling tests on the flocs of San Francisco Bay sediment in a graduated glass cylinder. It was shown that Eq. (3) is consistent with the kinetics of inter-particle collisions and aggregation during the settling of suspended flocs previously postulated by Overbeek[17], with [math]n = 1/3[/math].
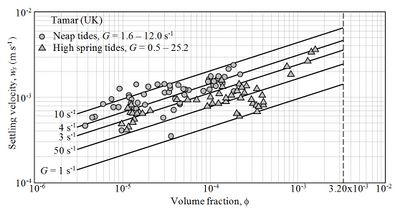
Returning to Eq. (1), in Fig. 5 field-collected data from a station in the Tamar estuary (UK) are included for two tidal conditions – high spring and neap (Manning [15]) – using an apparatus consisting of two components – LabSFLOC (Manning[18]) and INSSEV (Manning and Dyer[19]), which together permit optical image-based measurements of the settling velocity and the diameter as flocs fall in a column. The apparatus is taken on board the vessel and measurements are made immediately upon retrieving a sample of suspension at the desired depth below water surface. The velocity shear rate Eq. (2) was calculated from
[math]G= \Large [\frac{u_{*}^3}{\kappa \nu z_b}]^{0.5} \normalsize , \qquad (4)[/math]
where [math]u_*[/math] is the known bed friction velocity, [math]\rho_w= 1,015 \;[/math] kg m-3,[math]\; \kappa = 0.4[/math] is the von Karman constant, [math]\nu = 1.02 \times 10^{-6} \;[/math] m2/s and [math]z_b = 0.25 \;[/math] m is the nominal near-bed elevation representing the sampling depth. Values of the coefficients for lines from Eq. (1) are [math]a_0 = 10^{-4}, \; \phi_h = 3.2 \times 10^{-3}, \; \lambda_a = 10, \; \lambda_b = 0.01, \; n = 1/3[/math]. The [math]n[/math] value is consistent with [math]0.344 [/math] obtained from data on the settling of flocs of sediment from the San Francisco Bay in laboratory flumes, even though the hydraulic conditions were not entirely comparable with those in the bay (Mehta et al. [20]). The value [math]1/3[/math] is also supported by data from other estuaries (Winterwerp and van Kesteren[21]). For fixed values of [math]G[/math] (from [math]1[/math] to [math]50[/math] s-1), [math]w_s[/math] characteristically increases with [math]\phi[/math] as collisions between flocs/particles increase with particle concentration. The fifty-five data points for neap tide yield [math]2.34[/math] as the mean fractal dimension [math]D[/math] with a standard deviation [math]\sigma_D = 0.11[/math]. The 50 spring tide data points give [math]D = 2.32[/math] and [math]\sigma_D = 0.08[/math]. From this we may infer that variation in the tidal range did not have a significant impact on floc geometry.
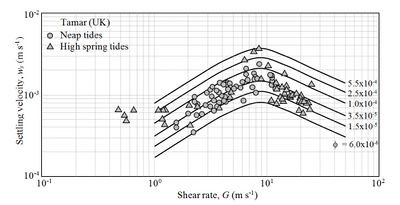
In Fig. 6 the Tamar data are replotted to emphasize the role of [math]G[/math] at constant [math]\phi[/math] ranging from [math]3.0 \times 10^{-6}[/math] to [math]5.5 \times 10^{-4}[/math] consistent with measured concentrations of suspended sediment. As turbulance increases, at [math]G \approx 10 \;[/math] s-1 the growth and breakup processes balance and [math]w_s[/math] attains a maximum. Further increase in [math]G[/math] results in the dominance of breakup and [math]w_s[/math] decreases. Data below about [math]1 \;[/math] s-1 suggest that at these low shear rates [math]w_s[/math] is not clearly dependent on [math]G[/math]. As the provenance of these low shear flocs is unknown it is reasonable to consider [math]1 \;[/math] s-1 to be the lowest value of [math]G[/math] at which Eq. (1) describes shear-induced aggregation.
Empirical formulas for the settling velocity of mud flocs have been determined by Soulsby et al. (2013[22]) for microflocs and macroflocs. Macroflocs are mainly agglomerates of microflocs, but are less stable than the smaller microflocs. Macroflocs have a higher fall velocity than microflocs because of their much greater size. The various factors that determine the fall velocity are captured in the following empirical formulas, for macroflocs [math] w_{M}[/math] and microflocs [math] w_{\mu}[/math], respectively:
[math] w_{M}=\Large\frac{g B_M}{G}\normalsize \left(\Large \frac{c}{ \rho}\normalsize \right)^k \left(\Large \frac{G d_\mu^2}{\nu}\normalsize \right)^{0.33} \exp \left[-\left( \Large \frac{u_{*M}}{\sqrt{\tau / \rho}}\normalsize \right)^{0.463} \right] , \qquad w_{ \mu}= \Large \frac{g B_\mu}{G}\normalsize \left(\Large \frac{Gd^2}{\nu}\normalsize \right)^{0.78} \exp \left[-\left(\Large \frac{u_{\mu}}{\sqrt{\tau / \rho}}\normalsize \right)^{0.66} \right] , \qquad (5)[/math]
where the index [math]M[/math] designates the macroflocs and the index [math]\mu[/math] the microflocs. The turbulent shear rate [math]G[/math] is given by Eq. (4). Other symbols stand for: [math]d[/math] the grainsize of the constituent primary particles and/or flocculi, [math]d_{\mu}[/math] the grainsize of the constituent microflocs, [math]\tau[/math] is the near-bed shear stress and [math]c [/math] the suspension concentration in [math] kg/l [/math]. For the Tamar and Gironde estuaries the following parameter values were established: [math] B_M = 0.13, \; B_{\mu} = 0.6, \; k = 0.22, \; u_{*M} = 0.067 m/s, \; u_{*\mu} = 0.025 m/s, \; d_\mu = 10^{-4} m, \; d = 10^{-5} m [/math]. The settling velocities observed in the Tamar and Gironde are 0.5-1 mm/s for microflocs and about 5 times larger for macroflocs.
Floc deposition
The volume deposition flux is, according to Eq. (1),
[math]F_s = w_s \phi (1 - \Large\frac{\tau_b }{\tau_d}\normalsize) = a(G){\phi }^{n+1} (1 - \Large\frac{\tau_b }{\tau_d}\normalsize), \qquad (6)[/math]
where [math]a(G)=w_{sh}(G) \phi_h^{-1}[/math], the bed shear stress [math]{{\tau }_{b}}={{\rho }_{w}}u_{*}^{2}[/math] and [math]\tau_d[/math] is called the critical shear stress for deposition. Deposition can occur only when [math]\tau_b[/math] is less than [math]\tau_d[/math].
In shallow estuaries, flocs are conveyed by current over the entire water depth [math]h[/math]. The deposition of flocs in terms of time-rate of decrease of [math]\phi[/math] is then given by
[math]h \Large \frac{d\phi }{dt} \normalsize = - F_s =- a(G) \normalsize \left( 1-\Large \frac{{{\tau }_{b}}} {{{\tau }_{d}}} \normalsize \right){{\phi }^{n+1}}, \qquad (7)[/math]
Solving for [math]\phi[/math] yields
[math]\phi (t)={{\phi }_{0}}{\Big[1+\Large \frac{a(G)n\phi _{0}^{n}}{h} \normalsize \left( 1-\Large \frac{{{\tau }_{b}}}{{{\tau }_{d}}} \normalsize \right)t \Big]^{-\Large \frac{1}{n}}} \normalsize , \qquad (8)[/math]
where [math]\phi_0[/math] is the value of [math]\phi[/math] at the start of deposition (e.g. at the beginning of a time-step in a numerical model), which causes [math]\phi(t)[/math] to decrease (Mehta et al. [20]).
If [math]w_s[/math] is constant, setting [math]n = 0[/math] and [math]a[/math] constant, then Eq. (7) yields
[math]\phi (t)=\phi _0 \; \exp\Big[-\Large \frac{w_s}{h} \normalsize \left( 1-\Large \frac{\tau_b}{\tau_d} \normalsize \right) \; t \Big], \qquad (9)[/math]
which is commonly known as the Krone equation with deposition flux [math]{{F}_{s}}={{w}_{s}}\phi[/math].
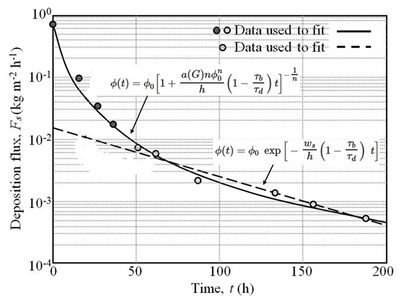
In Fig. 7, the Krone equation Eq. (9) and the generalized Krone equation Eq. (8) are plotted along with experimental data from a deposition test run in a flume ([math]h = 0.3 \;[/math] m, [math]\; \tau_b = 0.032 \;[/math] Pa, [math]\; \tau_d = 0.081 \;[/math] Pa) using sediment from Mare Island Strait in San Francisco Bay. The difference between the two curves is due to the inclusion of aggregation in Eq. (7) with [math]\phi_0 = 3.73 \times 10^{-3}, \; a = 4.3, \; n = 0.73[/math], which produced an order of magnitude greater net flux than from Eq. (9), with [math]\phi_0 = 4.11 \times 10^{-4}, \; w_s = 1.44 \times 10^{-6} \;[/math] m s-1. Thus it is evident that, in general, aggregation must not be ignored when modeling floc deposition.
Hindered settling
Hindered settling, which begins when [math]\phi[/math] exceeds [math]\phi_h[/math], is manifested as a decrease in the settling velocity with increasing [math]\phi[/math]. The particles are so close together that the rate at which they settle depends on the rate at which interstitial water can escape upward; this rate decreases as [math]\phi[/math] increases (and flow permeability decreases). A lutocline occurs at the depth of water at which hindered settling starts. According to Eq. (1) the maximum velocity achieved at the onset of hindered settling is dependent on the shear rate.
The simplest model for hindered settling is the Richardson and Zaki[23] equation
[math]{{w}_{s}}={{w}_{sh}}(G) \Big[1-k\left( \Large \frac{\phi }{{{\phi }_{h}}} \normalsize -1 \right) \Big]^{5} \quad ; \Large \frac{\phi }{{{\phi }_{h}}} \normalsize \ge 1, \qquad (10)[/math]
in which [math]k[/math] depends on the sediment. The exponent 5 (rounded from the experimental 4.65) was shown by the investigators to be consistent with the correction to Stokes law derived by considering the forces on a free-falling particle due to neighboring particles in the viscous regime. As [math]w_{sh}(G)[/math] is not always known, it may be taken as [math]w_{sh}(1)[/math] from Eq. (1), the lowest value arising from shear-induced aggregation, i.e.
[math]{{w}_{sh}}(1)={{a}_{0}} \Large \left( \frac{1+{{\lambda }_{a}}}{1+{{\lambda }_{b}}} \right) \normalsize . \qquad (11)[/math]
In Lake Apopka in central Florida settling velocities of organic-rich mud ([math]\rho_s = 1,873 \;[/math] kg m-3) were measured with LabSFLOC/INSSEV and also in a laboratory settling column. As shear rates in the lake were low, assuming [math]G = 1 \;[/math] s-1, Eqs. (1) and (10) are plotted in Fig. 8 along with the data.
ANNEX: Flocculation process and modelling
Since the settling velocity of the dynamically varying mud aggregate particles changes as the floc structure changes, many attempts have been made to account for flocculation. The first simple models were empirical relationship correcting the settling velocity with a factor as a function of instantaneous concentration and turbulent dissipation rate. The next generation introduced a kinetic equation describing the aggregation and break-up of flocs [24]. Following, more elaborate population balance equation modelling has been introduced, applied to multiple floc size fractions. In order to reduce the computational effort for large scale applications, new strategies have been proposed to work with a continuous particle size distribution [25] and to distinguish at least two floc populations [26] .
Clay mineral particles nominally in the range of 0.1 to 10 μm are present in flocs. The floc diameter [math]d_f[/math] is determined by aggregation (processes) including floc growth and breakup. Floc growth depends on the particle-particle collision frequency which in turn is contingent upon the concentration of particles and the collision mechanism. Turbulent shear represented by the rate [math]G[/math] is the main collision mechanism in estuarine waters except during times close to slack water when collisions are promoted by flocs settling at different velocities and to a lesser extent by Brownian diffusion (Winterwerp and van Kesteren[21]). Note that Brownian diffusion does play an important role in the aggregation of colloids, which can become large enough to be in the sedimentary size range (Mayer and Wells[27]). Shear produces strong flocs compared to the other two mechanisms and its role is manifested as dependence of floc diameter on the Kolmogorov micro-length scale of turbulent eddies (Liggett[28], Fugate and Friedrichs[29]). Floc breakup occurs when high-velocity collisions induce a stress that exceeds the shear strength of the floc, and in the absence of collisions by flow-induced shearing.
Whether the floc diameter [math]d_f[/math] increases or decreases with time [math]t[/math] is determined by the balance
[math]\Large \frac{d}{dt} \normalsize {{d}_{f}} = \text{rate}\ \text{of}\ \text{growth}\,\text{-}\,\text{rate}\ \text{of}\ \text{breakup}.\qquad(A1)[/math]
Kranenburg [30] argued that clay flocs demonstrate fractal properties reasonably well, i.e. their structures are geometrically fairly similar, as defined by the fractal dimension [math]D[/math]. Under this assumption the above equation can be represented as (Winterwerp and van Kesteren[21])
[math]\Large \frac{d}{dt} \normalsize {{d}_{f}} =\ {{k}_{g}}{{\rho }_{s}}{{\phi }^{n}}Gd_{f}^{2}-\ {{k}_{b}}{{G}^{3/2}}d_{f}^{2}({{d}_{f}}-{{d}_{p}}), \qquad (A2)[/math]
in which [math]D[/math] is taken as 2, a typical mean value, [math]\phi= C/\rho_s[/math] is the solids volume fraction, [math]C[/math] is the sediment concentration (in units of, e.g., kg m-3), [math]k_g[/math] and [math]k_b[/math] are sediment dependent growth and breakup coefficients, respectively, and [math]n[/math] embodies the intensity of aggregation as mentioned again later. Son and Hsu[31] proposed a modified form of Eq. (A2) by relaxing the restriction that the floc yield strength and the fractal dimension are constant.
Starting with seed mineral particles, under conditions that promote growth, [math]d_f[/math] will increase and eventually reach an equilibrium value [math]d_{fe}[/math] when the growth and breakup rates become equal. In that case [math]d d_f /d t = 0 [/math] and from Eq. (A2)
[math]{{d}_{fe}}= \Large\frac{{{k}_{g}}}{{{k}_{b}}}\frac{{{\rho }_{s}}}{\sqrt{G}} \normalsize {{\phi }^{n}}, \qquad (A3)[/math]
where we have assumed [math]d_p/d_{fe} \lt \lt 1[/math], which is typically reasonable. This relationship indicates that [math]d_{fe}[/math] varies with [math]{\phi}[/math] as well as [math]G[/math].
The wet bulk density [math]\rho_f[/math] of flocs is usually much lower than the material density [math] \rho_s[/math]. Stokes law for the settling velocity [math]w_s[/math] can be written as
[math]{{d}_{f}}= \Large [\frac{18 \rho_w \nu {{w}_{s}}}{g\Delta {{\rho }_{f}}}]^{0.5} \normalsize , \qquad (A4)[/math]
in which the diameter [math]d_{fe}[/math] is simply denoted as [math]d_f[/math] and [math]\Delta \rho_f = \rho_f - \rho_w[/math] is the excess floc density. From this and image-based measurements of [math]w_s[/math] and [math]d_f[/math] in a settling column [math]\Delta \rho_f[/math] can be calculated.
Related articles
- Dynamics of mud transport
- Sediment deposition and erosion processes
- Coastal and marine sediments
- Mud
References
- ↑ Maggi, F. 2005. Flocculation dynamics of cohesive sediment. PhD dissertation, TU Delft.
- ↑ 2.0 2.1 Migniot, C. 1968. A study of the physical properties of different very fine sediments and their behavior under hydrodynamic action, La Houille Blanche 7: 591-620 (in French, with abstract in English).
- ↑ McCave, I.N., Manighetti, B. and Robinson, S.G. 1995. Sortable silt and fine sediment size/composition size slicing: parameters for palaeocurrent speed and palaeoceanography. Paleoceanography 10: 593-610.
- ↑ van Olphen, H. 1977. An Introduction to Clay Colloid Chemistry, 2nd ed., Wiley.
- ↑ Eisma, D. 1986. Flocculation and de-flocculation of suspended matter in estuaries, Netherlands Journal of Sea Research 20(2/3): 183-199.
- ↑ Gerbersdorf, S.U., Bittner, R., Lubarsky, H., Manz, W. and Paterson, D.M. 2009. Microbial assemblages as ecosystem engineers of sediment stability, Journal of Soils and Sediments 9: 640-652
- ↑ 7.0 7.1 Law, B.A., Milligan, T.G., Hill, P.S. and Bugden, G.L. 2021. The effect of concentration on particle settling in the Minas Basin, Nova Scotia. Continental Shelf Research 223, 104448
- ↑ Kranenburg, C. 1994. On the fractal structure of cohesive sediment aggregates. Estuarine, Coastal and Shelf Science 39: 451-460
- ↑ Grabowski, R.C., Droppo, I.G. and Wharton, G. 2011. Erodibility of cohesive sediment: the importance of sediment properties. Earth Science Reviews 105 (3-4): 101-12
- ↑ Skinnebach, K.H., Fruergaard, M. and Andersen, T.J. 2019. Biological effects on flocculation of fine-grained suspended sediment in natural seawater. Estuarine, Coastal and Shelf Science 228, 106395
- ↑ Linley, E.A.S. and Field, J.G. 1982. The nature and significance of bacterial aggregation in a nearshore upwelling ecosystem. Estuarine, Coastal and Shelf Science 14: 1-11
- ↑ Mietta, F., Chassagne, C., Manning, A.J. and Winterwerp, J.C. 2009. Influence of shear rate, organic matter content, pH and salinity on mud flocculation. Ocean Dynamics 59: 751–763
- ↑ 13.0 13.1 Hill, P.S., Voulgaris, G. and Trowbridge, J.H. 2001. Controls on floc size in a continental shelf bottom boundary layer. J. Geophys. Res. 106: 9543–9549
- ↑ van Leussen, W. 1994. Estuarine macroflocs: their role in fine-grained sediment transport, PhD thesis, Utrecht University, the Netherlands.
- ↑ 15.0 15.1 15.2 Manning, A.J. 2001. A study of the effects of turbulence on the properties of flocculated mud. Ph.D. Thesis, University of Plymouth, Plymouth, UK.
- ↑ Krone, R.B. 1962. Flume studies of the transport of sediment in estuarial shoaling processes, Final Report, Hydraulic Engineering Laboratory and Sanitary Engineering Research Laboratory, University of California, Berkeley.
- ↑ Overbeek, J.T.G. 1952. Colloid Science, Vol. 1, in: Kinetics of Flocculation, H.R. Kruyt ed., Elsevier, 278-300.
- ↑ Manning, A.J. 2006. LabSFLOC – A laboratory system to determine the spectral characteristics of flocculating cohesive sediments, Technical Report TR 156, HR Wallingford, Wallingford UK.
- ↑ Manning, A.J. and Dyer, K.R. 2002. The use of optics for the in-situ determination of flocculated mud characteristics, Journal of Optics A: Pure and Applied Optics 4: S71-S81.
- ↑ 20.0 20.1 20.2 Mehta, A.J., Manning, A.J. and Khare, Y.P. 2014. A note of the Krone deposition equation and significance of floc aggregation, Marine Geology 354: 34-39.
- ↑ 21.0 21.1 21.2 Winterwerp, J.C., van Kesteren, W.G.M. 2004. Introduction to the Physics of Cohesive Sediment in the Marine Environment. Elsevier.
- ↑ Soulsby, R.L., Manning, A.J., Spearman J. and Whitehouse, R.J.S. 2013. Settling velocity and mass settling flux of flocculated estuarine sediments. Marine Geology 339: 1–12
- ↑ Richardson, J.F. and Zaki, W.N. 1954. The sedimentation of a suspension of uniform spheres under conditions of viscous flow, Chemical Engineering Science 3: 65-73.
- ↑ Winterwerp, J.C. 2002. On the flocculation and settling velocity of estuarine mud. Continental Shelf Research 22: 1339-1360
- ↑ Maerz, J., Verney, R. , Wirtz, K. and Feudel, U. 2011. Modeling flocculation processes: Intercomparison of a size class-based model and a distribution-based model. Continental Shelf Research 31: S84–S93.
- ↑ Lee, B.J., Toorman, E.A. Moltz, F. and Wang, J. 2011. A two-class population balance equation yielding bimodal flocculation of marine or estuarine sediments. Water Research 45: 2131-2145.
- ↑ Mayer, L.M. and Wells, M.L. 2011. Aggregation of colloids in estuaries, In: Wolanski E. and McLusky D.S. eds.,Treatise on Estuarine and Coastal Science, Vol. 4, Academic Press, 143-159.
- ↑ Liggett, J.A. 1994. Fluid Mechanics, McGraw-Hill.
- ↑ Fugate, D.C. and Friedrichs, C.T. 2003. Controls on suspended aggregate size in partially mixed estuaries, Estuarine Coastal and Shelf Science 58: 389-404
- ↑ Kranenburg, C. 1994. The fractal structure of cohesive sediment aggregates, Estuarine Coastal and Shelf Science 39(5): 451-460
- ↑ Son, M., Hsu, T.-J. 2011. The effects of flocculation and bed erodibility on modeling cohesive sediment resuspension, Journal of Coastal Research 116, C03021, doi:10.1029/2010JC006352