Seawater intrusion and mixing in estuaries

We describe in this article the physical processes involved in seawater intrusion and mixing in estuaries under the influence of tidal motion and explain some simple methods for deriving quantitative estimates. Several of the dispersion mechanisms discussed in this article are illustrated by dye experiments shown in Estuarine dispersion: dye experiments in the Eastern Scheldt scale model. This article is largely based on experience from large-scale experiments to unravel tidal dispersion processes in the Eastern Scheldt by Dronkers and van de Kreeke (1986 ) and on the book Mixing in Inland and Coastal Waters by Fischer et al. (1979).

Introduction

Estuaries are generally defined as semi-enclosed transition zones between river and sea. The intrusion of seawater in estuaries determines the salinity distribution. Salinity is usually expressed as the weight in grams of all dissolved salts per kilogram of water or alternatively according to the Practical Salinity Scale (see Salinity). The seawater intrusion limit is determined by the location in the estuary where the difference with river salinity is below a small number, e.g. 0.1. Seawater intrusion is mainly due to tides and to the influence of the density difference between seawater and river water on currents and turbulence (this influence is often termed 'buoyancy effects', see the article Estuarine circulation for further details). It is counteracted by freshwater inflow from rivers, groundwater, and other sources. Seawater intrusion in estuaries is an important phenomenon to man and nature: it limits freshwater availability for human and agricultural use, and it determines the type of habitats and species that can develop in an estuarine environment. Besides, density driven currents and salinity play a role in estuarine turbidity and sedimentation processes.

The net effect of estuarine mixing processes during a tidal cycle on along-channel seawater intrusion or on net along-channel spreading (diffusion) of dissolved substances is generally called longitudinal dispersion. This net effect is described by a longitudinal dispersion coefficient [math]K^{(x)}[/math]. The different mixing processes contributing to longitudinal dispersion are termed dispersion mechanisms. In well-mixed and partially mixed estuaries these mixing processes are dominantly induced by tidal motion; the net effect on seawater intrusion is called tidal longitudinal dispersion or simply tidal dispersion. Longitudinal dispersion and the flushing time of an estuary are related concepts. The combined effect of all tidal dispersion processes on seawater intrusion is sometimes called 'tidal pumping'. Here we use the term 'tidal pumping' only for the fraction of outflowing estuarine water that is replaced by 'new' seawater at the estuarine mouth.

Seawater intrusion has a strong variability. At a fixed station, the salinity increases during high tide and is greatest at high water; the salinity decreases during low tide and is smallest at low tide. Besides, seawater intrusion is small with high river discharge and strong with low river discharge. Change in seawater intrusion with river discharge is more gradual than the variability due to flood and ebb. If the river discharge varies on a time scale greater than the flushing time of the estuary, the tide-averaged salinity distribution tends towards an equilibrium distribution. The longitudinal dispersion coefficient can be determined by measuring the salinity distribution under equilibrium conditions. This coefficient generally varies along the estuary and depends on the river discharge.

The dispersion processes that are responsible for seawater intrusion determine the flushing time as well as the residence time of dissolved substances in an estuary. This holds similarly for the residence time of micro-organisms that are carried along passively (not swimming, floating or settling) with the water.

Definitions and assumptions

The estuarine mouth is defined as the transition between zones of channeled tidal flow (tidal discharge mainly following the channel axis) and non-channeled flow (discharge deviated along the open coast). The estuarine head is defined here as the location where the seawater influence on the salinity is (almost) nil; this location depends on the river discharge. We are interested in the net effect of tidal mixing processes during a tidal cycle on seawater intrusion along the estuarine axis, defined as the [math]x[/math]-axis ([math]x=0[/math] at the estuarine mouth). This makes sense only if we assume that the salinity difference between the estuarine mouth and the estuarine head is much greater than salinity differences in lateral ([math]y[/math]-axis) and vertical ([math]z[/math]-axis) directions. Stratified estuaries where salinity differences between bottom and surface are comparable to the salinity differences between estuarine mouth and estuarine head are dealt with in the article Salt wedge estuaries. The estuaries considered in this article are often designated as well-mixed or partially mixed estuaries.

Successive tidal cycles are not identical. Determining the net effect of tidally induced mixing processes requires integration over a large number of tidal cycles. To circumvent this complication, we assume that successive tidal cycles are sufficiently comparable (no extreme spring-neap variation) to enable the definition of a representative cyclic tide. This assumption will be used throughout this article.

Random walk

Under certain conditions, explained below, estuarine mixing processes can be described in terms of a random walk. For simplicity we consider a tidal basin with small river inflow (river discharge much smaller than tidal discharges). Situations where river flow exerts a substantial influence on estuarine water motion are dealt with in the article Estuarine circulation. Water motion is described as the average motion of a very large number of individual water parcels. If individual water parcels follow identical paths during flood (inflow) and ebb (outflow) all seawater parcels entering the basin during flood will be expelled during ebb: no seawater intrusion will occur. In reality this will not happen; mixing processes ensure that individual water parcels follow different paths during flood and ebb. Water parcels move back and forth in a tidal basin for some time before finally leaving the estuary and being evacuated offshore. We call [math]\tau_x [/math] the flushing time of water parcels in the tidal basin; it is defined as the average time it takes for a fluid parcel to travel from the upstream boundary of the estuary to the sea. During this time, water parcels also move in lateral and vertical directions, due to flow circulations and turbulent eddies. The time scale for vertical mixing, [math]\tau_z [/math], and the time scale for lateral mixing, [math]\tau_y [/math], are related to the vertical and lateral turbulent diffusion coefficients, [math]K^{(z)} [/math] and [math]K^{(y)} [/math], by the relationships [math]\tau_z=D^2/ K^{(z)}[/math] and [math]\tau_y=B^2/ K^{(y)}[/math], respectively. The time scales [math]\tau_y [/math] and [math]\tau_z [/math] indicate the time during which the motions of individual water parcels remain correlated; after a longer time they have lost the memory of their initial position [math](y_0,z_0)[/math] in the estuarine cross-section. The probability that after this time they will be in a cross-sectional position [math](y,z)[/math] from where their net displacement during the next tidal cycle will be in landward direction is then equal to the probability that they will be in a position where their net displacement will be in seaward direction (we assume that the influence of river discharge is small and can be ignored). The cross-sectional mixing time [math]\tau[/math] is approximately equal to the lateral mixing time [math]\tau_y[/math], if we assume that lateral mixing takes more time than vertical mixing; this is the case for most well-mixed or partially mixed wide estuaries. If [math]\tau[/math] is much smaller than the longitudinal flushing time [math]\tau_x[/math] of water parcels in the estuary, the path in longitudinal direction of a water parcel then follows a random walk. This condition only holds for estuaries of sufficient length; it may not be the case for wide, multichannel estuaries. The longitudinal displacements [math]X (1), X (2), … [/math] in successive time intervals [math]\tau[/math] are uncorrelated, by choosing [math]\tau=nT[/math] equal to an integer number of cyclic tidal periods such that [math]\tau \ge T[/math]. After a time [math]t_N[/math] comprising a large number [math]N[/math] of time intervals [math]\tau[/math] the average net displacement of all water parcels initially situated in a given cross-section of the tidal basin is approximately zero in the absence of river discharge:

[math]E[\sum_{i=0}^N X (i)] \; \approx \; 0 , \qquad(1)[/math]

where [math]E[..][/math] is the ensemble average over all water parcels initially situated in a given cross-section of the tidal basin. Here we have assumed [math]t_N \le \tau_x[/math]. Because [math]X(i)[/math] and [math]X(j)[/math] are uncorrelated for [math]i \ne j[/math], we have [math]E[X(i)X(j)] \approx 0 \;[/math] for [math]i \ne j[/math] and [math]E[X(i)^2] \approx \overline{X^2} \;[/math] is the average square displacement over a time [math]\tau[/math]. The average square displacement over the time interval [math]t_N =N \tau[/math] is therefore given by

[math]E[(\sum_{i=0}^N X (i))^2] \; = \; E[\sum_{i=0}^N X (i) \; \sum_{j=0}^N X (j)] \; \approx \; \sum_{i=0}^N E[X (i)^2] \; \approx \; t_N \; \overline{X^2} / \tau . \qquad(2)[/math]

Figure 1: Longitudinal dispersion coefficients at different locations in the Eastern Scheldt and Ems-Dollard estuaries.

The square of the average displacement of water parcels in the tidal basin thus increases linearly with time. This is precisely the characteristic of a diffusion process of a dissolved substance with concentration [math]s(x,t)[/math]. This diffusion process is described by the equation

[math]\Large \frac{\partial s}{\partial t} \normalsize = K^{(x)}\Large \frac{\partial^2 s}{\partial x^2} \normalsize , \quad [/math] with diffusion coefficient [math]\quad K^{(x)}= \Large \frac{\overline{X^2} }{ 2 \tau} \normalsize . \qquad(3)[/math]

The random walk assumption [math] \tau_x \gt \gt \tau[/math], expressing the condition that particle paths become uncorrelated for time intervals larger than the cross-sectional mixing time [math]\tau[/math] but much smaller than the longitudinal mixing time [math]\tau_x[/math], thus implies that salt transport by seawater intrusion processes, [math]Q_{disp}[/math], can be represented by a gradient-type transport formula,

[math]Q_{disp} = - A_0 K^{(x)}\Large \frac{ds_0}{dx} \normalsize , \qquad(4) [/math]

where [math]s_0[/math] is the tidally averaged salinity concentration, [math]s_0(x)=\lt s(x,t)\gt [/math], [math] K^{(x)}[/math] is the longitudinal dispersion coefficient and [math]A_0=\lt A\gt [/math] (the brackets <> represent the average over a tidal cycle). The dispersion coefficient [math] K^{(x)}[/math] has the important property that it does not depend explicitly on the salinity distribution in the estuary , but only on the flow characteristics during the tidal cycle (which may be influenced by the salinity distribution, by the way). The magnitude of the random displacements depends on the location [math]x [/math] in the estuary; the longitudinal dispersion coefficient [math] K^{(x)}[/math] is thus a function of [math]x [/math]. This is illustrated in Fig. 1 for the Eastern Scheldt and Ems-Dollard estuaries.

Longitudinal dispersion mechanisms

Mixing processes, such as those described by the random walk model, cause seawater to intrude further and further into the estuary. However, seawater is also expelled from the estuary due to the inflow of river water at the estuarine head. Seawater intrusion is stabilised when the net upstream salt transport by mixing processes equals the net downstream salt transport by the fluvial discharge. This can be represented by the following formulas.

The fresh water discharge [math]Q_R[/math] is given by

[math]Q_R=-\lt A\overline{\overline{u}}\gt \equiv - \large \frac{1}{T}\int_0^T \int_{-B/2}^{B/2} \int_0^D \normalsize u(x,y,z,t) dzdy dt \qquad(5) [/math]

and the net total salt flux (by mixing processes and river discharge) is given by

[math]Q_S=\lt A\overline{\overline{us}}\gt \equiv \large \frac{1}{T} \int_0^T \int_{-B/2}^{B/2} \int_0^D \normalsize u(x,y,z,t)s(x,y,z,t) dzdydt , \qquad(6) [/math]

where [math]A(x,t)[/math] is the estuarine cross-section, [math]D(x,y,t)[/math] the instantaneous local water depth and [math]B(x,t)[/math] the estuarine width, [math]u[/math] the longitudinal current velocity and [math]s[/math] the salinity. The brackets stand for averaging over the tidal period [math]T[/math] (assuming a cyclic tide) and the overbars stand for averaging over the depth and the width. The coordinate [math]x[/math] follows the upstream positive longitudinal direction (along the thalweg), the coordinate [math]y[/math] the lateral direction and the coordinate [math]z[/math] the upward positive vertical direction.

We call [math] s_0 \equiv \lt \overline{\overline{s}}\gt [/math] the salinity averaged over the estuarine cross-section [math]A[/math] and the tidal period. We may then decompose

[math]Q_S=Q_{disp} - Q_R s_0, \quad Q_{disp} = \lt A\overline{\overline{u(s-s_0)}}\gt \qquad(7) [/math] .

This decomposition singles out the fresh water discharge (the term [math] Q_R s_0[/math] ) as a mechanism for flushing seawater out of the estuary, while the term [math] Q_{disp}[/math] represents the sum of all processes contributing to seawater intrusion. These processes are:

• Horizontal circulations in the estuary (mainly the net relative displacement of water masses circulating between ebb and flood channels and the net relative displacements due to geometry-induced eddies, followed by lateral mixing of these water masses);
• Horizontal tidal straining (lateral mixing between water masses which are advected at different speeds, due to lateral gradients in the longitudinal velocity);
• Vertical circulation in the estuary, also called estuarine circulation (seawater intrusion induced by the density-driven net displacement of near-surface water relative to near-bottom water, followed by mixing over the vertical);
• Vertical tidal straining (vertical mixing between water masses advected at different speeds due to vertical gradients in the longitudinal velocity);
• Lateral mixing of water masses captured in "dead zones" with the main flow;
• Chaotic dispersion, related to the chaotic character of particle trajectories when travelling through a complex field of tide-generated eddies;
• Tidal pumping at the inlet, which is defined here as the partial replacement of the ebb tidal prism with ‘new’ seawater flowing in from the nearshore zone during flood.

These different dispersion processes will be discussed in the following.

Analytical expressions for the longitudinal dispersion coefficient

Under strongly simplifying conditions it is possible to derive analytical expressions for the longitudinal dispersion coefficient. These assumptions are:

• the estuarine geometry does not vary strongly in [math]x[/math]-direction over distances comparable to or larger than the tidal excursion;
• the cross-section of the estuarine main channel can be represented approximately a rectangular shape.

We also have the condition [math]\tau\lt \lt \tau_x[/math], cross-sectional mixing takes place on a time scale much shorter than the estuarine flushing time. In the following we consider different seawater intrusion processes under these conditions and present an approximate analytical expression for the dispersive transport produced by each process.

Dispersion by residual circulation

Fist we consider seawater intrusion caused by estuarine circulation: the up-estuary near-bottom flow caused by the higher density of seawater relative to estuarine water. The estuarine circulation is represented by the velocity component

[math]u_0 (z)= \lt u\gt -\lt \overline{u}^z\gt , \qquad(8) [/math]

where the brackets [math]\lt u\gt [/math] stand for averaging over the tidal period and [math]\overline{u}^z [/math] for averaging over the vertical. The averaging is done in a frame moving with the cross-sectional mean velocity. The longitudinal dispersive transport can be estimated by a procedure outlined by G.I. Taylor . The result is

[math] K^{(x)}= f_0^{(z)} \tau_z \overline{(u_0)^2}^z , \qquad(9) [/math]

with [math] f_0^{(z)} [/math] a coefficient of the order of 0.1 . The formula (9) shows that the dispersion coefficient increases with increasing mixing time [math]\tau_z[/math]. However, there is a limit, because of the assumption [math]\tau_z \lt \lt \tau_x[/math].

For the dispersion coefficient related to lateral horizontal residual circulation a similar formula can be derived, replacing in the expression for [math] K^{(x)}[/math] everywhere [math]z[/math] by [math]y[/math]. Approximate semi-empirical expressions for the vertical mixing time [math]\tau_z[/math] and the lateral mixing time [math]\tau_y[/math] are given in the section #Time scales for vertical and lateral mixing.

Figure 2: Circulation cells in the Western Scheldt related to ebb- and flood-dominated channels.

Estuarine circulation is an important seawater intrusion mechanism in estuaries with a single deep (dredged) channel and small to moderate tide. Lateral circulations are important in wide natural estuaries with a complex geometry (meandering main channel , secondary channels, channel bars and tidal flats) and strong tides. The dominance of lateral circulations for seawater intrusion relative to vertical circulations appears in the analytical expression of [math] K^{(x)}[/math] through the much larger lateral mixing time [math]\tau_y [/math] compared to the vertical mixing time [math]\tau_z [/math]. The presence of distinct ebb and flood channels is a major cause of lateral circulation in wide estuaries, see for example Fig. 2. However, density gradients related to seawater intrusion also produce lateral circulations (see Estuarine circulation), which contribute often even more to longitudinal dispersion than the vertical density-induced circulation .

Dispersion by tidal straining

If residual circulations are weak, dispersion is mainly caused by tidal straining, the relative displacement of water masses due to vertical and horizontal gradients in the tidal current velocity. In river flow, the usual term for this mixing mechanism is shear dispersion. Seawater intrusion in narrow deep estuaries is primarily caused by vertical tidal velocity gradients, whereas lateral tidal velocity gradients are important in wide estuaries. We present formulas for vertical tidal straining; the expressions for lateral tidal straining are similar. The process of longitudinal dispersion through tidal straining is explained in Fig. 3.

The velocity component [math]u_1 (z,t) [/math] responsible for vertical tidal straining is

[math]u_1= u-\overline{u}^z , \qquad(10) [/math]

where [math]\overline{u}^z[/math] is the depth-average current velocity. By a procedure outlined by Holley, Harleman and Fischer , the following first-order estimate of the longitudinal dispersion coefficient is obtained:

[math] K^{(x)}\approx f_1^{(z)} \Large \frac{\tau_z \lt \overline{ u_1^2}^z\gt }{1+( f_2^{(z)} \tau_z / T)^2 } \normalsize . \qquad(11) [/math]

[math]T[/math] is the tidal period. The coefficients [math] f_1^{(z)}, f_2^{(z)} [/math] depend on the velocity profile; order-of-magnitude estimates are [math] f_1^{(z)} \sim 0.1-0.2[/math] and [math] f_2^{(z)} \sim 0.5-1 [/math].

Longitudinal dispersion produced by lateral tidal straining can be expressed by a formula similar as for vertical tidal straining. Dispersion by tidal straining is largest if the time scale for vertical or lateral mixing is on the order of [math]T/ f_2[/math]. The time scale for vertical mixing is generally smaller than the tidal period and the time scale for lateral mixing is generally larger. Dye experiments illustrating dispersion by lateral tidal straining are shown in Estuarine dispersion: dye experiments in the Eastern Scheldt scale model. A derivation of the expressions (9) and (11) is given in Appendix A for lateral shear dispersion.

It should be realised that longitudinal dispersion is not simply the sum of transport processes related to circulation and straining. Circulation causes not only a net relative displacements of water masses in the estuary, but it also influences tidal straining.

Figure 3: Schematic representation of longitudinal dispersion by a vertical gradient in the tidal current [math]u(z,t)[/math]. A patch of dye is introduced homogeneously over the vertical when flood starts at low-water slack tide ([math]t=0[/math]). The patch of dye is stretched by the tidal current while being mixed vertically by turbulent diffusion. The time scale for vertical mixing [math]\tau_z[/math] is assumed of the same order as the tidal period [math]T[/math]. The tidal cycle is represented by four discrete time steps, illustrating the combined action of turbulent vertical mixing and shear of the current in the vertical. The stretching of the dye patch combined with vertical diffusion results in a strong longitudinal spreading after a tidal cycle.

Time scales for vertical and lateral mixing

A difficulty for the practical use of the preceding expressions for longitudinal dispersion arises from the uncertainty associated with estimating the vertical and (especially) lateral mixing times, [math]\tau_z=D^2/ K^{(z)}[/math] and [math]\tau_y=B^2/ K^{(y)}[/math]. In the case of a logarithmic velocity profile (in the absence of density stratification), the vertical diffusion coefficient is given by [math] K^{(z)}=0.4z(1-z/D)u_*[/math], where [math]u_* \approx 0.05 U[/math] is the friction velocity and [math]U[/math] is the flow velocity. This yields a longitudinal dispersion coefficient [math] K^{(x)}\approx 6u_*D[/math], for steady flow . However, in the case of buoyant flows, vertical diffusion can be much slower (smaller [math] K^{(z)}[/math]), leading to stronger longitudinal dispersion. Lateral diffusion is strongly dependent on the geometry of the estuary. The lateral diffusion coefficient is generally expressed as [math] K^{(y)}\approx \alpha u_* D[/math]. An empirical estimate for moderately meandering channels is [math]\alpha \approx 0.6 [/math] and a model estimate is [math] \alpha \approx 150 (B/ R)^2 [/math] , where [math]B[/math] is the channel width and [math]R[/math] is a characteristic channel bend radius.

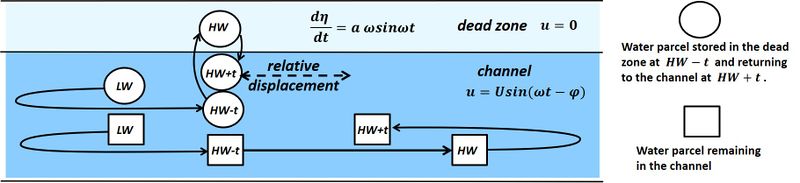
Dispersion by "dead zones"

Fig. 4. The Krabbenkreek, a large creek that contributes to longitudinal dispersion in the Eastern Scheldt estuary (Netherlands)

Estuaries usually have an irregular shape with areas along the main channel where the water flow has only a weak or even no longitudinal component. Such areas may correspond to tidal creeks. An example is the Krabbenkreek in the Eastern Scheldt estuary, shown in Fig. 4. Longitudinal flow is also weak on large tidal flats along the channel. These areas are sometimes called "dead zones". These dead zones should not be confused with the anoxic zones, called "dead zone" in ecology. Water that has flooded dead zones along the main estuarine channel often empties during falling tide with a different salinity than the water passing at that time in the channel. This can be caused by a phase difference [math]\phi[/math] between the flow on and off the dead zone relative to the phase of the channel flow. It can also be caused by mixing of the water inside the dead zone. The result after each tidal cycle is in both cases a net longitudinal dispersion of estuarine waters. The processes underlying longitudinal estuarine dispersion can be considered as special cases of tidal straining. Mathematical derivations are given in Appendix B for a few strongly idealized situations. Based on the analytical expressions, estimates can be derived for the contribution of the dead zones to the estuarine longitudinal dispersion. For illustration, we use as an example the following order of magnitudes: [math]A \sim 10^4 m^2[/math] is the channel cross-section area, [math]U \sim 1 m/s[/math] is the maximum tidal current velocity in the channel, [math]\phi \sim 45' , \, \sin \phi \sim 0.37[/math] is the phase delay of the tidal current velocity in the channel relative to lateral exchange flows. Other notations used are: [math]T[/math] is the tidal period, [math]x[/math] is the along-channel distance from the creek entrance, [math]L=UT/\pi[/math] is the tidal excursion and [math]l=L \sin \phi[/math].

The idealized situations considered in Appendix B are:

Dispersion by a shallow tidal creek
We consider a tidal creek with bed level around low water (LW) or below. The creek tidal volume is [math]V^0_S[/math] with an order of magnitude of 10⁶ m³ in the numerical examples. The along channel distance to the creek entrance is [math]x[/math].

First case: the tidal creek in- and outflow advances the channel flow by [math]\phi[/math] radians. When mixing in the tidal creek is ignored, the dispersion in the estuary is locally enhanced, corresponding to an increase of the dispersion coefficient by [math]\quad K^{(x)}(x) = \dfrac{ V^0_S}{A T} |x| \sqrt{1 - \dfrac{x^2}{L^2 \sin^2 \phi}} \, , \qquad (12)[/math]

where [math]|x|[/math] is the distance seaward from the creek. In the numerical example, the maximum dispersion coefficient is of the order of 6 m²/s.

Second case: the water entering the creek is completely mixed before outflow; the phase [math]\phi=0[/math]. The estuarine dispersion coefficient is enhanced by [math]\quad K^{(x)}(x) = \dfrac{V^0_S L}{AT} \, \dfrac{|x|}{L} \, (1-\dfrac{|x|}{L}) \, .\qquad (13)[/math]

The maximum contribution to the estuarine dispersion is of the order of 8 m²/s.

Dispersion by a tidal flat We consider a tidal flat that borders the tidal channel over its entire length. The bed level of the tidal flat is around LW and the width [math]b_S[/math] of the tidal flat is of the order of 1000 m in the numerical examples.

First case: the tidal flat in- and outflow advances the channel flow by [math]\phi[/math] radians. When mixing in the tidal creek is ignored the dispersion in the estuary is locally enhanced with a dispersion coefficient [math]\quad K^{(x)} = \frac{1}{3} \dfrac{r l^2}{T} = \dfrac{r}{3 \pi^2} U^2 T \sin^2 \phi \, . \qquad (14)[/math]

The contribution to estuarine longitudinal dispersion is of the order of 100 m²/s.

Second case: the tidal flat in- and outflow is in phase with the channel flow, [math]\phi=0[/math]. The water entering the tidal flat during rising tide is entirely mixed over the width of the tidal flat when flowing back to the channel. The contribution to the estuarine dispersion is given by [math]\quad K^{(x)} = \frac{1}{3} \dfrac{a b_S}{A} \dfrac{L^2}{T} = \dfrac{r}{6 \pi^2} U^2 T \, . \qquad (15)[/math]

The numerical example gives an enhanced longitudinal estuarine dispersion of about 300 m²/s. This large value is not realistic, as complete mixing on the tidal flat is unlikely to occur.

Fig. 5. Schematic of flow pattern at a channel constriction.

Another type of "dead zones" occurs at constrictions of the estuarine channel, see Fig. 5. At a channel constriction, the flood flow initially concentrates in a jet, so the downstream lateral sides of the channel ("dead zones") are only later filled by the flood flow via recirculating currents. However, most of this lateral water is absorbed into the ebb current almost without delay, resulting in a displacement of water parcels stored in the dead zone relative to water parcels following the center of the channel. A similar relative displacement is caused on the seaward side of the channel constriction by the ebb current jet. The longitudinal dispersion caused by a channel constriction strongly depends on the local bathymetry. Therefore, a simple analytical expression for this dispersion mechanism cannot be given. The same holds for flow separation zones that occur in channel bends.

Dye experiments illustrating longitudinal dispersion by dead zones are shown in Estuarine dispersion: dye experiments in the Eastern Scheldt scale model.

Dispersion by deterministic chaos

Figure 6: Stretching of an initially rectangular patch of dye in a few tidal cycles, according to a 2D numerical hydrodynamic model of the central part of the Western Wadden Sea .

Dye experiments show that dispersion in wide estuaries with complex geometry generally proceeds in an irregular way, by advection of fluid parcels through a field of geometry-induced tidal eddies. The result is very different from turbulent diffusion (i.e. diffusion by a cascade of turbulent eddies of progressively decreasing size). Parts of the dye can be trapped within gyres without any significant turbulent diffusion, while other dye patches can be highly stretched in the flow direction. Strong stretching occurs in particular in the interface zones between tidal eddies, see Fig. 6. Zimmerman (1986) described the dispersion process in such systems as the result of Lagrangian chaos produced by 'a tidal whirlpool'. Fluid parcels can be dispersed over the entire length of the estuary before lateral mixing has taken place. In this case, the random walk description of tidal dispersion is no longer valid. Zimmerman showed that longitudinal dispersion can still be described as a random process, even if turbulent mixing is completely absent. He called this random process “deterministic chaos” . In his model, fluid parcels are dispersed by moving along chaotic orbits through a lattice of tidal eddies. Most dispersion is generated by eddies with a size [math]\lambda[/math] comparable to the tidal excursion length [math]L[/math] . This suggests that the longitudinal dispersion coefficient for chaotic mixing should be proportional to

[math] K^{(x)}\propto UL \, , \qquad(16) [/math].

where [math]U[/math] represents the magnitude of the tidal current velocity. The size of the eddies also depends on the basin with [math]B[/math]. A field study in Willapa Bay (US Pacific coast) suggests that chaotic dispersion could be described by a dispersion coefficient [math] K^{(x)}= 0.06 UB[/math] . If the lateral mixing time [math]\tau_y[/math] is comparable to or larger than the flushing time [math]\tau_x [/math], the representation of the dispersive transport [math] Q_{disp}[/math] by the product of a dispersion coefficient and the local salinity gradient is no longer valid.

Dispersion by tidal pumping

The term 'tidal pumping' is often used for all the estuarine dispersion processes that are not due to density-driven estuarine circulation. A different convention is used here, in which salt intrusion by tidal pumping is related to the fraction of estuarine outflow water that is replaced by seawater on the next flood. In this definition, tidal pumping refers to the rate of renewal of estuarine water in the outflow region and therefore on tidal inflow-outflow hydrodynamics. In general, the seawater entering the estuary during flood has a higher salinity compared to the average salinity of estuarine water flowing out into the sea during ebb. Tidal exchange through the inlet therefore constitutes a major mechanism of seawater intrusion, importing seawater into the estuary as far as the tidal flood incursion.

Outflow of estuarine water often has a jet-like character, whereas flood water enters the estuary more evenly distributed from different directions, depending on the tidal phase, see Fig. 7. The inflowing flood water therefore contains ‘new’ seawater from the sides of the ebb channel. Replacement of outflowing estuarine water by "new" seawater is enhanced when river discharge is high, because the ebb jet is concentrated in a surface layer (salinity stratification), whereas seawater inflow is more evenly distributed over the vertical.

Figure 7: Schematic representation of seawater intrusing by tidal pumping.

We call [math]\alpha[/math] the replacement rate of outflowing estuarine water by seawater during a tidal cycle. For small fresh water discharge, the corresponding dispersion coefficient at the estuarine mouth is given by

[math]K^{mouth} = \alpha \Large \frac{L^2 }{2T} , \normalsize \qquad(17) [/math]

where [math]L=\int_{flood} u(t)dt [/math] is the tidal excursion at the estuarine mouth. Savenije derived the following empirical expression for [math]\alpha[/math], based on observations suggesting that the renewal of estuarine water in the mouth area depends on the buoyancy of the ebb jet:

[math]\alpha=\Large \frac{2800 \pi D}{l_A} \normalsize \sqrt{Ri_E} . \qquad(18) [/math]

In this expression [math]D[/math] is the depth and [math]l_A[/math] the convergence length of the estuary in the outflow zone (assuming exponential convergence of the cross-section in the outflow zone, [math] A(x) \sim exp(-x/l_A)[/math]);

[math]Ri_E[/math] is the Richardson estuary number [math]Ri_E=g \Delta \rho Q_R T^3 / ( \pi^2 \rho B L^3)[/math];

[math] \Delta \rho / \rho[/math] is the relative density difference seawater-fresh water and [math]B[/math] the estuarine width at the mouth. The value of [math]\alpha[/math] should not exceed 1. Because of its dependency on buoyancy, tidal pumping is a major mechanism of seawater intrusion in estuaries during periods of high river flow.

However, tidal pumping at the estuarine sea inlet depends not only on the buoyancy of the estuarine outflow jet. The fraction of estuarine water that re-enters the estuary on the next flood is strongly influenced by alongshore currents in the coastal zone. Wind is generally the main driving agent for alongshore currents through Ekman transport and geostrophic flow. Strong alongshore currents can carry estuarine outflow water away from the inlet and prevent it from returning on the next flood. Alongshore currents can also transport the water outflowing from adjacent estuaries to the inlet.

The salinity of the seawater near the inlet can be influenced by upwelling or downwelling currents, especially for estuaries located on narrow shelves (see Ekman transport). Upstream currents bring high salinity water to the estuary entrance, while downstream currents can prevent the ebb current plume from spreading out to sea and thus increase the fraction of estuary water that returns to the estuary on the next flood.

Residence time scale

The residence time [math]\tau_r[/math] is defined as the average time a water parcel, which is initially located at a distance [math]x[/math] from the sea boundary, will take to leave the estuary. If the fresh water discharge is zero or very small, and if the dispersion coefficient [math] K^{(x)}[/math] is assumed constant along the estuary, the residence time is given by random walk theory :

[math]\tau_r = \Large \frac{x^2}{2 K^{(x)}} \normalsize . \qquad(19) [/math]

The transit time [math]\tau_t=\tau_x[/math] is the average time it takes for a fresh water parcel to move through the estuarine zone to the sea. According to the random walk model, for small discharge [math]Q_R[/math],

[math]\tau_t = \dfrac{l^2}{2 K^{(x)}} , \qquad(20) [/math]

where [math]l[/math] is the estuarine length.

The transit time [math]\tau_t[/math] is closely related to the flushing time [math]\tau_f[/math] defined as (see Appendix C)

[math]\tau_f = V_{fresh} /Q_R \, , \qquad (21)[/math]

where [math]V_{fresh}[/math] is the fresh water volume in the estuary.

Experimental determination of the longitudinal dispersion coefficient

The dispersion coefficient [math] K^{(x)}[/math] can be determined experimentally in situations where the freshwater discharge [math]Q_R[/math] is constant over a period longer than [math]\tau_x[/math]. In that case the tidally averaged salinity distribution [math]\lt s(x,t)\gt [/math] is close to equilibrium, [math] \lt s(x,t)\gt \approx s_{eq}(x) [/math]. The total residual salt flux [math]Q_S[/math] approximately equals zero. We thus have (with the sign convention [math]Q_R \gt 0[/math])

[math]A K^{(x)}\Large \frac{ds_{eq}}{dx} \normalsize + Q_R s_{eq} = 0 . \qquad (22) [/math]

Values of the dispersion coefficient can be derived from measurements of the residual discharge [math]Q_R[/math] and the salinity distribution [math]s_0(x)[/math]. Estimates of longitudinal dispersion coefficients determined in this way are shown in Table 1. More detailed analyses show that the dispersion coefficient [math] K^{(x)}[/math] is a function of [math]x[/math] and [math]Q_R[/math]. The dependence of [math] K^{(x)}[/math] on [math]Q_R[/math] has two causes. It is related in the first place to the influence of the salinity distribution on the velocity flow field [math]u(x,u,z,t)[/math]; such an influence is due to salinity-induced density gradients (see Estuarine circulation). In the second place, it is related to the location of the freshwater-seawater transition zone. If this zone is situated near the estuarine mouth, the dispersion coefficient is strongly influenced by tidal pumping. This explains the high longitudinal dispersion coefficients for Rotterdam Waterway, Seine and Loire in Table 1, which are determined for situations with important river flow [math]Q_R/hb[/math]. The same holds, to a somewhat lesser degree, for the Elbe, Weser, Mekong and Sinnamary.

The influence of salinity-induced density gradients on the longitudinal dispersion coefficient is generally small in estuaries with complex topography and small river inflow ([math]Q_R/hb[/math] several orders of magnitude smaller than the tidal velocity). This is the case for many tidal lagoons, such as the Wadden Sea.

If a non-buoyant dissolved substance is introduced in the estuary, it will be mixed over the cross-section after a time [math]\tau[/math] . From that time, the longitudinal dispersion of the substance is similar to salinity dispersion (same dispersion coefficient). For a permanent discharge of a non-buoyant dissolved substance, the same dispersion coefficient applies in the estuarine zones where the substance is mixed over the estuarine cross-section.

Longitudinal dispersion coefficients derived from observed salinity distributions at constant river discharge. The figures for tidal range, depth and width are representative values for the zone with the strongest salinity gradient. Data from , , , , , , .

estuary	tidal range [math]2a[/math] [m]	depth [math]D[/math] [m]	width [math]B[/math] [km]	discharge [math]Q_R[/math] [m3/s]	dispersion coefficient [math] K^{(x)}[/math] [m2/s]
Bay of Fundy (Canada)	10	20	20	150	300
Bristol Channel (UK)	8	30	20	480	60
Chao Phraya (Thailand)	2.5	7.2	0.6	30	330
Corantijn (Surinam)	4.3	6.5	3	500	230
Delaware (US)	1.5	6.6	7	300	300
Eastern Scheldt (Netherlands)	3	12.5	2	60	200
Elbe (Germany)	3.3	12	2.5	750	700
Ems-Dollard (Netherlands)	3	9	4	100	275
Gambia (The Gambia)	1.2	8.7	4	2	200
Hudson (US)	1.6	11,6	2.2	100	110
Humber (UK)	5.5	12	3	250	300
Incomati (Mozambique)	5.5	2.9	0.6	1	10
Limpopo (Mozambique)	2.6	7	0.2	5	150
Loire (France)	4.5	9	0.9	825	900
Mae Klong (Thailand)	2	5.2	0.2	30	200
Maputo (Mozambique)	6.7	3.6	1.3	10	100
Mekong-Co Chien+Cung Hau (Vietnam)	2.1	7	4	2125	570
Mekong-Tran De+Dinh Anh (Vietnam)	2.8	8	3	2250	530
Mersey (UK)	7.5	20	1	80	400
Potomac (US)	1.4	8.4	9	110	70
Pungue (Mozambique)	5	11.5	1.8	20	140
Rotterdam Waterway (Netherlands)	0.9	15	0.6	1000	1000
St. Lawrence (Canada)	3	74	48	8500	200
Seine (France)	5.5	8	0.8	440	800
Sinnamary (Guiana)	2.3	3.8	0.3	100	560
Solo (Indonesia)	1.1	9.2	0.17	10	240
Tha Chin (Thailand)	2.9	5.3	0.2	10	270
Thames (UK)	4.5	12	3	60	100
Weser (Germany)	3.8	9	2	324	1000
Western Scheldt (Netherlands)	3.8	16	3.5	100	200

Related articles

Estuarine dispersion: dye experiments in the Eastern Scheldt scale model

Estuarine circulation

Salt wedge estuaries

Appendix A: Longitudinal dispersion by a shearing current

In this appendix we first reproduce the analysis of G.I. Taylor (1954) for the derivation of an analytical expression of the longitudinal dispersion coefficient related to vertical (turbulent) diffusion in a mean velocity field with a stationary circulation current. It may apply, for example, to the longitudinal dispersion of salinity produced by a density-driven net upstream flow near the bottom and a net downstream flow near the surface. The analytical model is an extreme simplification of real estuarine velocity fields. Major simplifications relate to the assumptions that the mean velocity field [math]u[/math] and the depth [math]h[/math] are uniform in longitudinal and lateral directions over the full tidal excursion and that vertical diffusion can be characterized by a uniform and constant eddy diffusion coefficient [math]K^{(z)}[/math]. The longitudinal and lateral coordinates [math]x, z[/math] refer to a reference frame moving with the cross-sectionally averaged tidal flow.

The mean velocity field with stationary vertical circulation in the moving reference frame is represented by

[math]u(z) = - U \cos(\large\frac{\pi z}{h}\normalsize) \, , \quad -h \lt z \lt 0 \, . \qquad (A1)[/math]

The salinity concentration is denoted [math]s(x,z,t)[/math]. The salt balance equation in the moving frame (salinity change by longitudinal advection and vertical diffusion) can be written

[math]\Large\frac{\partial s(x,z,t)}{\partial t}\normalsize + u(z) \Large\frac{\partial s(x,z,t)}{\partial x}\normalsize - \Large\frac{\partial }{\partial z}\normalsize \Big( K^{(z)} \Large\frac{\partial s(x,z,t)}{\partial z}\normalsize \Big) =0 \, . \qquad (A2)[/math]

We consider a stationary situation, [math]\Large\frac{\partial s(x,z,t)}{\partial t}\normalsize =0[/math]. The longitudinal salinity gradient [math]\Large\frac{\partial s(x,z,t)}{\partial x}\normalsize = \Large\frac{ds}{dx}\normalsize [/math] can be considered constant and uniform over the depth. The salt transport by longitudinal dispersion is then given by

[math] h K^{(x)} \Large\frac{ds}{dx}\normalsize = \int_{-h}^0 u(z) s(x,z) dz \, . \qquad (A3)[/math]

The salinity [math]s(x,z)[/math] can be found by integrating Eq. (A2) twice over the depth, considering that [math]K^{(z)} \Large\frac{\partial s}{\partial z}\normalsize =0[/math] at [math]z=-h[/math] (no salt transport through the bottom) and [math]\int_{-h}^0 u(z) dz =0[/math]. The result is

[math]s(x,z) = \Large\frac{1}{K^{(z)}}\frac{ds}{dx}\normalsize \int_{-h}^z dz' \int_{-h}^{z'} u(z'') dz'' \, . \qquad (A4)[/math]

Substitution in Eq. (A3) and using Eq. (A1) gives

[math]K^{(x)} = \Large\frac{U^2}{h K^{(z)}}\normalsize \int_{-h}^0 dz \cos(\large\frac{\pi z}{h}\normalsize) \int_{-h}^{z} dz' \int_{-h}^{z'} \cos(\large\frac{\pi z''}{h}\normalsize) dz'' \, . \qquad (A5)[/math]

The result is

[math]K^{(x)} = \Large\frac{h^2 U^2}{2 \pi^2 K^{(z)}}\normalsize = \Large\frac{U^2 \, \tau_z}{\pi^2}\normalsize \, , \qquad (A6)[/math]

where the vertical mixing time scale is given by

[math]\tau_z = \Large\frac{h^2}{2 K^{(z)}}\normalsize \, . \qquad (A7)[/math]

Shear dispersion can also be estimated by considering diffusion as a random walk process. In this approach, the longitudinal and vertical position of a fluid parcel are given by the stochastic variables [math](X(t), Z(t))[/math], and we have

[math]X(t) = \int_0^{t} u(X(t),Z(t),t) dt \, . \qquad (A8)[/math]

The mean velocity field [math]u(x,z,t)[/math] is averaged over the turbulent eddy time scale and is defined in a reference frame moving with the cross-sectionally averaged tidal flow. Without diffusion, a fluid parcel would not move in this reference frame.

We consider again a mean velocity field with a vertical circulation which is stationary in the moving reference frame,

[math]u(z) = - U \cos(\large\frac{\pi z}{h}\normalsize) \, , \quad -h \lt z \lt 0 \, . \qquad (A1)[/math]

where [math]h[/math] is the estuarine depth. According to the random walk model Eq. (3), the longitudinal dispersion coefficient is related to the net squared parcel displacement due to vertical diffusion in the time interval [math]0 \lt t \lt \tau_z[/math] ([math]\tau_z[/math] is the vertical mixing time scale and [math]E[ .. ][/math] the ensemble average over all possible parcel trajectories),

[math]K^{(x)} = \dfrac{E\big[X^2(\tau)\big]}{ 2 \tau_z } = \Large\frac{U^2}{2 \tau_z}\normalsize \int_0^{\tau_z} dt_1 \int_0^{\tau_z} dt_2 \; E\big[ \cos(\large\frac{\pi Z(t_1)}{h}\normalsize) \cos(\large\frac{\pi Z(t_2)}{h}\normalsize) \big] \, . \qquad (A9)[/math]

[math]E\big[ \cos(\large\frac{\pi}{h}\normalsize (Z(t_1)+Z(t_2))) \big] = 0[/math] because the ensemble average cannot depend on the initial phase of the random trajectory [math]Z(t)[/math]. Therefore,

[math]E\big[ \cos(\large\frac{\pi Z(t_1)}{h}\normalsize) \cos(\large\frac{\pi Z(t_2)}{h}\normalsize) \big] = \large\frac{1}{2}\normalsize E\big[ \cos(\large\frac{\pi}{h}\normalsize (Z(t_1)-Z(t_2))) \big] \, . \qquad (A10) [/math]

Now let [math]p(z,t)dz[/math] be the probability that a fluid parcel has traveled a distance between [math]z[/math] and [math]z+dz[/math] in a time [math]t[/math]. The probability density function [math]p(z,t)[/math] must satisfy the diffusion equation [math]\dfrac{h^2}{2 \tau_z}\dfrac{\partial^2 p}{\partial z^2}\normalsize = \dfrac{\partial p}{\partial t}[/math] and the conditions [math]p(z,0) = \delta(z)[/math] and [math]\int_{-h}^0 p(z,t) = 1[/math]. These conditions are satisfied by the function

[math]p(z,t) = \dfrac{1}{h} + \dfrac{2}{h} \sum_{n=1}^{\infty} \cos(\dfrac{n \pi z}{h}) \exp(-\dfrac{n \pi^2}{2 \tau_z} |t|) \, . \qquad (A11)[/math]

We therefore have

[math]E\big[\cos(\large\frac{\pi }{h}\normalsize (Z(t_1)-Z(t_2))) \big] = \int_{-h}^0 p(z, t_2-t_1) \cos(\dfrac{\pi z}{h}) dz \, .\qquad (A12) [/math]

Integration gives [math]E\big[\cos(\large\frac{\pi }{h}\normalsize (Z(t_1)-Z(t_2))) \big] = \exp(-\dfrac{\pi^2}{2 \tau} |t_2-t_1| ) \, .\qquad (A13) [/math]

Substitution in Eq. (A9) gives

[math]K^{(x)} = E\big[X^2(\tau)\big] / (2 \tau_z) = \dfrac{U^2}{4 \tau_z} \int_0^{\tau_z} dt_1 \int_0^{\tau_z} dt_2 \exp(-\dfrac{\pi^2}{2 \tau} |t_2-t_1| ) = \dfrac{U^2 \, \tau_z}{\pi^2} \Big(1 + \dfrac{2}{\pi^2} (\exp(-\dfrac{\pi^2}{2}) – 1) \Big) \approx \dfrac{U^2 \, \tau_z}{\pi^2} \, , \qquad (A14)[/math]

which is the same result as (A6).

A similar approach can be used for the case of a time varying gradient of the tidal velocity. We assume that random particle displacements perpendicular to the flow direction are not influenced by the flow strength. This assumption is equivalent to assuming that the eddy diffusion coefficient is independent of the tidal phase. Longitudinal dispersion is caused by so-called tidal straining, the lateral diffusion of a patch of a dissolved substance which is stretched by a cross-sectional velocity gradient of the tidal current.

In a reference frame moving with mean tidal current [math]\; U \sin(\dfrac{2 \pi t}{T}) [/math], we assume a lateral variation of the tidal velocity given by

[math]u(x,y,t) = U \, \cos(\large\frac{\pi y}{B}\normalsize) \, \cos(\large\frac{2 \pi t}{T}\normalsize + \phi) \, , \quad – B \lt y \lt B \, . \qquad (A15)[/math]

The estuarine width is [math]2B[/math] and [math]T[/math] is the tidal period. The random lateral motion is represented by the stochastic variable [math]Y(t)[/math]. The net squared parcel displacement due to lateral diffusion in the mean velocity field is now given by

[math]K^{(x)} = \dfrac{ E\big[X^2(\tau_y)\big]}{2 \tau_y} = \dfrac{U^2}{2 \tau_y}\normalsize \int_0^{\tau_y} dt_1 \int_0^{\tau_y} dt_2 \; E\Big[\cos(\large\frac{\pi Y(t_1)}{B}\normalsize) \cos(\large\frac{\pi Y(t_2)}{B}\normalsize) \Big] \; \cos(\large\frac{2 \pi t_1}{T}\normalsize + \phi) \cos(\large\frac{2 \pi t_2}{T}\normalsize + \phi) \, . \qquad (A16)[/math]

Since the dispersion coefficient cannot depend on the phase [math]\phi[/math] nor on the initial position of the random trajectory [math]Y(t)[/math], this expression can be simplified to

[math]K^{(x)} = \Large\frac{U^2}{4 \tau_y}\normalsize \int_0^{\tau_y} dt_1 \int_0^{\tau_y} dt_2 \; E\Bigg[\cos\big(\large\frac{\pi}{B}\normalsize (Y(t_1)-Y(t_2)) \big) \cos\big(\large\frac{2 \pi}{T}\normalsize (t_1 – t_2) \big) \Bigg] \, . \qquad (A17)[/math]

The probability [math]p(y,t)dy[/math] that a fluid parcel has traveled a distance between [math]y[/math] and [math]y+dy[/math] in a time [math]t[/math] is given by (similar to (A11))

[math]p(y,t) = \dfrac{1}{2B} + \dfrac{1}{B} \sum_{n=1}^{\infty} \cos(\dfrac{n \pi y}{B}) \exp(-\dfrac{n \pi^2}{2 \tau_y} |t|) \, . \qquad (A18)[/math]

Substitution in (A17) gives

[math]K^{(x)} = \Large\frac{U^2}{4 \tau_y}\normalsize \int_0^{\tau_y} dt_1 \int_0^{\tau_y} dt_2 \; \exp \big(-\dfrac{\pi^2}{2 \tau_y} |t_1-t_2| \big) \cos \big(\dfrac{2 \pi }{T} (t_1 – t_2) \big) \, . \qquad (A19)[/math]

Integration gives an analytical expression of the longitudinal dispersion coefficient related to shear diffusion produced by lateral variation with amplitude [math]U[/math] of the mean tidal current. Neglecting terms of order [math]\exp(-\dfrac{\pi^2}{2})[/math] with respect to 1, the result is

[math]K^{(x)} \approx \dfrac{ U^2 \tau_y}{\pi^2}\dfrac{1 - \dfrac{\pi^2}{2} +(1 + \dfrac{\pi^2}{2}) \Big(1+ \big( \dfrac{4 \tau_y}{T} \big)^2 \Big)}{ \Big(1+ \big( \dfrac{4 \tau_y}{T} \big)^2 \Big)^2 } \, . \qquad (A20)[/math]

If the lateral mixing time is larger than the tidal period, [math]4\tau_y \gt \gt T [/math], then [math] K^{(x)}\approx 0.15 \, \dfrac{T^2 U^2}{\tau_y} \, . \qquad (A21)[/math]

If the lateral mixing time is much smaller, [math]4 \tau_y \lt \lt T[/math], then [math] K^{(x)}\approx \dfrac{2 \tau_y U^2}{\pi^2}\normalsize \, . \qquad (A22)[/math]

Longitudinal dispersion by tidal straining is greatest when the lateral mixing time scale is a little less than half the tidal period.

If [math]\tau_y \approx 3T/8[/math], the dispersion coefficient [math] K^{(x)}\approx 2.2 \dfrac{ T U^2 }{\pi^2}\normalsize \, . \qquad (A23)[/math]

The physical interpretation is as follows. If the lateral mixing time scale [math]\tau[/math] is very short, there is hardly any longitudinal shear dispersion, because a patch of solute is spread all the time almost homogeneously over the estuarine width and moves up and down the estuary as a plug with the mean tidal current. An equivalent statement is that the net displacement of fluid parcels is almost uncorrelated with their instant lateral position in the estuary. If, on the other hand, the mixing time scale is very long, a patch of solute will be stretched over a large longitudinal distance by a residual circulation before it is mixed laterally, resulting in a large longitudinal dispersion. The net longitudinal displacement of fluid parcels will thus be strongly correlated with their instant lateral position in the estuary. However, if the time scale of lateral mixing is very long compared to the tidal period, a lateral gradient in the tidal current will contribute little to longitudinal dispersion, because the stretching of a solute patch during flood (inflow) is reversed during ebb (outflow) before lateral diffusion occurs (see Figure 3).

Appendix B: Dispersion by dead zones

A longitudinally uniform estuary with a prismatic channel (mean cross-sectional area [math]A[/math]) is bordered by a tidal flat of width [math]b_S[/math]. The tidal flat level corresponds to the low tidal level (level at [math]t=0[/math]). The longitudinal velocity on the tidal flat is nil; the tidal flat constitutes a "dead zone". Within the estuary we consider a long straight section where the tide level is represented by [math]\eta(t)= - a \cos \omega t[/math] and the tidal velocity by [math]u=U \sin (\omega t -\phi)[/math]. The tidal amplitude is [math]a[/math], the tidal radial frequency is [math]\omega = 2 \pi /T[/math] and the phase [math]\phi[/math] is the delay of the horizontal tide with respect to perfect quadrature with the vertical tide. The salt concentration [math]s(x,t)[/math] in the channel is advected with the tidal velocity without changing the gradient [math]ds/dx=ds_0/dx[/math]. The gradient [math]ds_0/dx[/math] is assumed to be constant throughout the straight estuarine section.

No mixing, non-zero phase shift [math]\phi[/math]

Our first assumption is that salt is transported only by tidal advection. No mixing occurs when the tidal flat is flooded between low water (LW, [math]t=0[/math]) and high water (HW, [math]t=T/2[/math]) and when the tidal flat is emptied in the channel during falling tide ([math]T/2\lt t\lt T[/math]). In this case, water parcels that enter the tidal flat at time [math]t[/math] experience a net seaward displacement [math]\; \Delta X(t)= - l \, \sin \omega t\, ,\; l=(2U/\omega) \sin \phi \;[/math] when flowing back into the channel compared to water parcels that travel all the time in the channel, see Fig. B1. This relative displacement generates a net dispersive transport.

Fig. B1. Dispersion by an intertidal "dead zone" along a tidal channel. The figure illustrates the case of a phase shift [math]\small \phi[/math] between the vertical tidal motion ([math]\small d\eta /dt[/math]) and the horizontal tidal motion ([math]\small u(t)[/math]). The paths of two fluid parcels are shown, both starting from the same location at low water ([math]\small t=0[/math]). The first parcel (the square) follows the tidal motion in the channel, while the second parcel (the circle) is stored in the dead zone around high water in a time interval [math]\small [T/2-t, T/2+t][/math]. Without mixing, the latter parcel returns to the channel at time [math]\small T/2+t[/math] at the same position [math]\small X_1(t)=(U/\omega)[\cos \phi - \cos(\pi - \omega t - \phi)][/math] where it entered the dead zone. This is seaward from the position [math]\small X_2(t)=(U/\omega)[\cos \phi - \cos(\pi + \omega t - \phi)][/math] at that time of the parcel that remained in the channel. The relative seaward displacement of particles leaving the dead zone at time [math]\small T/2-t[/math] is given by [math]\small \Delta X(t) = - (2U / \omega) \sin \phi \sin \omega t .[/math] The result is longitudinal dispersion: a net relative displacement during the tidal cycle of fluid parcels remaining in the channel compared to fluid parcels temporarily stored in the dead zone.

Dispersion by a creek
We consider first a tidal flat of small longitudinal width [math]dx[/math], corresponding to a tidal creek perpendicular to the channel. The location of the creek in the estuary is taken as [math]x=0[/math]. The water volume in the creek is [math]\; V_S= b_S \, dx \, (a + \eta(t)) \;[/math] ; the high water volume [math]\; V^0_S= 2 \, a\, b_S \, dx \;[/math]. The amount of salt entering the creek in the interval [math][t, t+dt][/math] is given by [math]\; dM_S = \dfrac{d V_S}{dt} s(0,t) \, dt = \frac{1}{2} V^0_S \sin \omega t \, s(0,t) \, \omega dt \;[/math].

We now consider particle trajectories in the channel starting from low water ([math]t=0[/math]) landward from a cross-sectional plane [math]x[/math]. The water parcels that enter the creek at time [math]t[/math] on their journey through the estuary will be displaced seaward over a distance [math]\Delta X(t)[/math]. They will cross the plane [math]x[/math] during ebb tide if [math]\Delta X(t) \lt x \;[/math] (by our convention of positive flood direction, [math]x[/math] and [math]\Delta X(t)[/math] are both negative). This yields a net seaward salt transport trough the plane [math]x[/math] given by

[math]M_1 = - \int_0^{T/2} \dfrac{d V_S}{dt} s(0,t) \, \Theta(x-\Delta X(t)) \, \omega dt , \qquad (B1)[/math]

where the Heaviside step function [math]\Theta[/math] is defined as [math]\Theta(x)=1, x\gt 0 \, ; \; \Theta(x) =0, x\lt 0[/math].

In order to close the water balance, at each time [math]t[/math] a compensating landward transport must occur through the plane [math]x[/math], which is given by

[math]M_2 = \int_0^{T/2} \dfrac{d V_S}{dt} s(x,t) \, \Theta(x-\Delta X(t)) \, \omega dt . \qquad (B2)[/math]

The net dispersive transport through the plane [math]x[/math] is therefore

[math]M(x) = M_1+M_2 = \int_0^{T/2} \dfrac{d V_S}{dt} \big( s(x,t) -s(0,t) \big) \, \Theta(x-\Delta X(t)) \, \omega dt . \qquad (B3)[/math]

Because the salt gradient is assumed independent of [math]t[/math], this expression can be simplified,

[math]M(x) = - \frac{1}{2} V^0_S \, x \, \dfrac{ds_0}{dx} \, \int_0^{T/2} \Theta(x+ l \sin \omega t) \, d\cos \omega t , \qquad (B4)[/math]

where we have substituted [math]\Delta X(t)= - l \sin \omega t[/math]. The condition [math]x\gt -l \sin \omega t[/math] is equivalent to [math]|\cos \omega t|\lt \sqrt{1-x^2/l^2}[/math]. Evaluation of the integral gives

[math]M(x) = - \, V^0_S \dfrac{ds_0}{dx} \, |x| \, \sqrt{1 - \dfrac{x^2}{l^2}} . \qquad (B5)[/math]

The dispersion coefficient [math] K^{(x)} (x)[/math] defined by [math]M(x) = - K^{(x)} \,A \, T\, \dfrac{ds_0}{dx}[/math] is given by

[math] K^{(x)} (x) = \dfrac{ V^0_S}{A T} |x| \sqrt{1 - \dfrac{x^2}{l^2}} \, , \qquad (B6) [/math]

where [math]|x|[/math] is the distance seaward from the creek. The maximum value at [math]x=-l/\sqrt{2}[/math] is

[math]\quad K^{(x)}_{max} = \dfrac{1}{2\pi} \dfrac{V^0_S U}{A} \sin \phi . \qquad (B7)[/math]

Dispersion by an along-channel tidal flat
As a second case we consider a "dead zone" consisting of a tidal flat running along the channel with constant width [math]b_S[/math] and bed level at tidal low water. This tidal flat contributes to net tidal salt transport in similar way as the tidal creek case. Instead of considering a narrow dead zone with length [math]dx[/math], we have to integrate the time integral (B4) over [math]x[/math],

[math]M = a b_S \dfrac{ds_0}{dx} \int dx \int_0^{T/2} \sin \omega t \, x \, \Theta(x-\Delta X(t)) \, \omega dt . \qquad (B8)[/math]

Inverting the [math]x[/math] and [math]t[/math] integrations we have

[math]M = a b_S \dfrac{ds_0}{dx} \int_0^{T/2} \sin \omega t \, \int_{-l \sin \omega t}^0 x dx \, \omega dt . \qquad (B8)[/math]

Evaluation of the integral gives

[math]M = - \frac{1}{2} a b_S l^2 \dfrac{ds_0}{dx} \int_0^{\pi} sin^3 t dt = - \frac{2}{3} a b_S l^2 \dfrac{ds_0}{dx} . \qquad (B9)[/math]

The dispersion coefficient is given by [math]\quad K^{(x)} = \frac{1}{3} \dfrac{r l^2}{T} = \dfrac{r}{3 \pi^2} U^2 T \sin^2 \phi , \qquad (B10) [/math]

where [math]r=\dfrac{2 a b_S}{A}[/math] is the relative tidal flat volume.

Another way to find this result is to integrate (B6) over [math]x[/math].

One may also consider a trajectory [math]X(\tau)=x +\dfrac{L}{2} \big(\cos(\tau -\phi) - \cos \phi\big)[/math], where [math]\tau=\omega t[/math]. The water parcels stored in the dead zone along this trajectory cross a fixed plane [math]x_0[/math] only in landward direction and not in seaward direction if [math]X(\tau)\gt x_0[/math] and [math]X(\tau)+\Delta X(\tau)\lt x_0[/math], with [math]\Delta X(\tau)= - l \, \sin \tau[/math]. Taking into account the compensating landward transport through the plane [math]x_0[/math], the net salt transport is given by

[math]M = a \, b_S \int_0^{\pi} d \tau \, \sin \tau \, \int dx \, \Theta \big(X(\tau)-x_0 \big) \, \Theta \big(x_0-X(\tau)-\Delta X(\tau) \big) \big( c(x_0,t)-c(X(t),t) \big) = - a \, b_S \, \dfrac{ds_0}{dx} \, \int_0^{\pi} d \tau \sin \tau \, \int_0^{-l\sin \tau} x dx[/math],

where we have used [math]c(x_0,t)-c(X(t),t) = \Big( x_0-X(t) \Big) \dfrac{ds_0}{dx}[/math] and substituted the definitions of [math]X(t)[/math] and [math]\Delta X(t)[/math]. The result is identical to (B8).

Complete mixing, no phase shift

Dispersion by a creek
Our second assumption is that complete mixing takes place on the tidal flat, while advection dominates in the channel. We focus on particle trajectories that start at low water at a position [math]x[/math] seaward from the creek, [math]\; X(t) = x +\dfrac{L}{2}(1-\cos \omega t) \; [/math], where [math]L=UT/\pi[/math] is the tidal excursion. Water parcels travelling along these trajectories can enter the creek located at [math]x=0[/math] if [math]t_0\lt t\lt T/2[/math], where [math]t_0[/math] is defined as

[math]\cos \omega t_0 = 1 + \dfrac{2x}{L} . \qquad (B11)[/math].

Now consider a trajectory [math]X_0(t)= -\dfrac{L}{2}(1+\cos \omega t)[/math] that reaches the creek at HW ([math]t=T/2[/math]). We call [math]s_1[/math] the salinity along this trajectory, [math]s_1 \equiv s(0,T/2)=s(X_0(T/2),T/2)=s(X_0(t),t)=s(0,t) + X_0(t) \dfrac{ds_0}{dx}[/math]. The salinity entering the creek is thus given by

[math]s(0,t) = s_1 - X_0(t) \dfrac{ds_0}{dx} = s_1 + \dfrac{L}{2}(1+\cos \omega t) \dfrac{ds_0}{dx}. \qquad (B12)[/math]

The salinity in the creek at HW, after complete mixing, is given by

[math]\overline{s(0)} =\dfrac{1}{V^0_S} \int_0^{T/2} \dfrac{dV_S}{dt} s(0,t) dt = \frac{1}{2} \int_0^{T/2} \sin \omega t \Big( s_1 + \dfrac{L}{2}(1+\cos \omega t) \dfrac{ds_0}{dx} \Big) \omega dt = s_1 + \dfrac{L}{2}\dfrac{ds_0}{dx} . \qquad (B13) [/math]

The amount of salt [math]x[/math] that enters the creek and passes the plane [math]x[/math] after exiting the creek is given by

[math]M = - \int_0^{t_0} \dfrac{dV_S}{dt} s(0,t) dt - \int_{T/2}^{T/2+t_0} \dfrac{dV_S}{dt} \overline{s(x,0)} dt . \qquad (B13)[/math]

Substitution of (B12) and (B13) gives

[math]M = - \frac{1}{4} V^0_S \, L \dfrac{ds_0}{dx} \Bigg[\int_0^{t_0} \sin \omega t (1+\cos \omega t ) \omega dt + \int_{T/2}^{T/2+t_0} \sin \omega t \, \omega dt \Bigg] \, . \qquad (B14)[/math]

Integration and substituting (B11) gives [math]\quad M = - \dfrac{V^0_S}{L} \, |x |\, (L-|x|) \dfrac{ds_0}{dx} = - K^{(x)} \, A \, T \dfrac{ds_0}{dx} \, , \qquad (B15) [/math]

where [math]|x|[/math] is the distance seaward from the creek. The maximum dispersion occurs for [math]x=– (L/2)[/math], giving

[math] K^{(x)}_{max} = \dfrac{1}{4 \pi} \dfrac{V^0_S \, U}{A} . \qquad (B16)[/math]

Dispersion by an along-channel tidal flat
The dispersion by complete mixing on a tidal flat that extends uniformly along the tidal channel is directly found by integrating (B15). Therefore we write [math]\; V^0_S = 2 \, a \, b_S \, dx . \;[/math] The integral covers the interval [math]-L \lt x \lt 0[/math], the distance over which mixing on the tidal flat produces dispersive transport in the estuary. The result is

[math] K^{(x)} = \frac{1}{3} \dfrac{a b_S}{A} \dfrac{L^2}{T} = \dfrac{r}{6 \pi^2} U^2 T . \qquad (B17)[/math]

Other analytical estimates of estuarine longitudinal dispersion by dead zones have been published by Okubo (1967), Dronkers (1978) and MacVean and Stacey (2011). These estimates, which are similar to the ones derived above, are based on different approaches and different approximations.

Appendix C: Flushing time scale

Using Eq. (22), the salt water volume of the estuary is given by

[math]V_{salt} = \int_0^l A \exp \big( - \large\frac{Q_R x}{A K^{(x)}}\normalsize \big) dx \, . \qquad (B1) [/math]

We assume [math]A[/math] and [math] K^{(x)}[/math] uniform along the estuary and [math]\; \exp \big( - \large\frac{Q_R l}{A K^{(x)}}\normalsize \big) \lt \lt 1 \;[/math]. After substituting [math]\tau_t = \dfrac{l^2}{2 K^{(x)}} [/math] the integral yields

[math]V_{salt} = \Large\frac{A^2 K^{(x)}}{Q_R}\normalsize = \Large\frac{V^2}{2 Q_R \, \tau_t}\normalsize , \;[/math] where [math]V= A\, l[/math] is the total estuarine volume.

If the salt and fresh water volumes in the estuary are of the same order, we find the following relation between the transit time scale [math]\tau_t[/math] and the flushing time scale [math]\tau_f[/math] :

[math]\tau_t \approx \Large\frac{2 V_{fresh}}{Q_R}\normalsize = 2 \tau_f \, .[/math]

References

The main author of this article is Job Dronkers Please note that others may also have edited the contents of this article. Citation: Job Dronkers (2025): Seawater intrusion and mixing in estuaries. Available from http://www.coastalwiki.org/wiki/Seawater_intrusion_and_mixing_in_estuaries [accessed on 10-08-2025] For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Dronkers J