Travel cost method
Definition of Travel cost method:
A Surrogate Market Approach technique for valuing ecosystems or environmental resources that takes the costs people pay to visit an ecosystem as an expression of its recreational value.
This is the common definition for Travel cost method, other definitions can be discussed in the article
|
This article deals with the Travel Cost Method, which is often used in evaluating the economic value of recreational sites. This is particularly important in the coastal zone because of the level of use and the potential values that can be attached to the natural coastal and marine environment.
The Travel Cost Method (TCM) is one of the most frequently used approaches to estimating the use values of recreational sites. The TCM was initially suggested by Hotelling[1] and subsequently developed by Clawson [2] in order to estimate the benefits from recreation at natural sites. The method is based on the premise that the recreational benefits at a specific site can be derived from the demand function that relates observed users’ behaviour (i.e., the number of trips to the site) to the cost of a visit. One of the most important issues in the TCM is the choice of the costs to be taken into account. The literature usually suggests considering direct variable costs and the opportunity cost of time spent travelling to and at the site. The classical model derived from the economic theory of consumer behaviour postulates that a consumer’s choice is based on all the sacrifices made to obtain the benefits generated by a good or service. If the price ([math]p[/math]) is the only sacrifice made by a consumer, the demand function for a good with no substitutes is [math]x=f(p)[/math], given income and preferences. However, the consumer often incurs other costs ([math]c[/math]) in addition to the out-of-pocket price, such as travel expenses, and loss of time and stress from congestion. In this case, the demand function is expressed as [math]x = f(p, c)[/math]. In other words, the price is an imperfect measure of the full cost incurred by the purchaser. Under these conditions, the utility maximising consumer’s behaviour should be reformulated in order to take such costs into account. Given two goods or services [math]x_1, x_2[/math], their prices [math]p_1, p_2[/math], the access costs [math]c_1, c_2[/math] and income [math]R[/math], the utility maximising choice of the consumer is:
[math]max \, U = u(x_1,x_2) \quad subject \, to \quad (p_1+c_1)x_1+(p_2+c_2)x_2=R . \qquad (1)[/math]
Now, let [math]x_1[/math] denote the aggregate of priced goods and services, [math]x_2[/math] the number of annual visits to a recreational site, and assume for the sake of simplicity that the cost of access to the market goods is negligible ([math]c_1 \approx 0[/math]) and that the recreational site is free ([math]p_2=0[/math]). Under these assumptions, equation (1) can be written as:
[math]max \, U = u(x_1,x_2) \quad subject \, to \quad p_1x_1+c_2x_2=R . \qquad (2)[/math]
Under these conditions, the utility maximising behaviour of the consumer depends on:
- a) his preferences [math]u(x_1, x_2) [/math],
- b) his budget [math]R[/math],
- c) the prices of the private goods and services [math]p_1[/math] and
- d) the access cost to the recreational site [math]c_2[/math].
The TCM is based on the assumption that changes in the costs of access to the recreational site [math]c_2[/math] have the same effect as a change in price: the number of visits to a site decreases as the cost per visit increases. Under this assumption, the demand function for visits to the recreational site is [math]x_2=f(c_2)[/math] and can be estimated using the number of annual visits as long as it is possible to observe different costs per visit. The basic TCM model is completed by the weak complementarity assumption, which states that trips are a non-decreasing function of the quality of the site, and that the individual forgoes trips to the recreational site when the quality is the lowest possible[3],[4]. There are two basic approaches to the TCM: the Zonal approach (ZTCM) and the Individual approach (ITCM). The two approaches share the same theoretical premises, but differ from the operational point of view. The original ZTCM takes into account the visitation rate of users coming from different zones with increasing travel costs. By contrast, ITCM, developed by Brown and Nawas[5] and Gum and Martin[6], estimates the consumer surplus by analysing the individual visitors’ behaviour and the cost sustained for the recreational activity. These are used to estimate the relationship between the number of individual visits in a given time period, usually a year, the cost per visit and other relevant socio-economic variables. The ITCM approach can be considered a refinement or a generalisation of ZTCM[7].
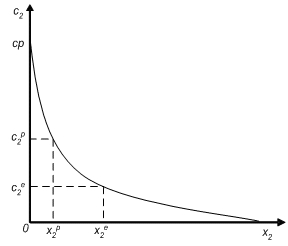
The Figure depicts the expected relationship between the number of visits and cost per visit, given other variables, showing that the number of visits decreases as the cost per visit increases. If we assume that all users have the same preferences and the same income, the number of visits is a function of the cost per visit:[math]x_2 = g(c_2) . \qquad (3)[/math]
The demand function can also be estimated for non-homogeneous sub-samples introducing among the independent variables income and socio-economic variables representing individual characteristics[8]. Therefore, if an individual incurs [math]c_2^e[/math] per visit, he chooses to do [math]x_2^e[/math] visits a year, while if the cost per visit increases to [math]c_2^p[/math] the number of visits will decrease to [math]x_2^p[/math]. The cost [math]cp[/math] is the choke price, that is the cost per visit that results in zero visits. The annual user surplus (the use value of the recreational site) is easily obtained by integrating the demand function from zero to the current number of annual visits, and subtracting the total expenditures on visits.
Related articles
- Contingent Valuation Method
- Hedonic Evaluation Approach
- Value Transfer
- Economic Value
- Total Economic Value
- Socio-economic evaluation
- Non-use value: bequest value and existence value
- Values of amenities in coastal zones
- Multifunctionality and Valuation in coastal zones: concepts, approaches, tools and case studies
- Multifunctionality and Valuation in coastal zones: introduction
References
- ↑ Hotelling, H. (1949), Letter, In: An Economic Study of the Monetary Evaluation of Recreation in the National Parks, Washington, DC: National Park Service.
- ↑ Clawson, M. (1959), Method for Measuring the Demand for, and Value of, Outdoor Recreation. Resources for the Future, 10, Washington, DC.
- ↑ Freeman, A.M. III. (1993). The Measurement of Environmental and Resource Values: Theory and Method, Washington, DC: Resources for the Future.
- ↑ Herriges, J.A., C. Kling and D.J. Phaneuf (2004), 'What’s the Use? Welfare Estimates from Revealed Preference Models when Weak Complementarity Does Not Hold', Journal of Environmental Economics and Management, 47 (1), pp. 53-68.
- ↑ Brown, W.G. and F. Nawas (1973), 'Impact of Aggregation on the Estimation of Outdoor Recreation Demand Functions', American Journal of Agricultural Economics, 55, 246-249.
- ↑ Gum, R.L. and W.E.Martin (1974), 'Problems and Solutions in Estimating the Demand for and Value of Rural Outdoor Recreation', American Journal of Agricultural Economics, 56, 558-566.
- ↑ Ward, F.A. and D. Beal (2000), Valuing Nature with Travel Cost Method: A Manual, Northampton: Edward Elgar.
- ↑ Hanley, N. and C.L. Spash (1993), Cost Benefit Analysis and the Environment, Aldershot, UK: Edward Elgar.
Please note that others may also have edited the contents of this article.
|