Wave ripple formation

From Coastal Wiki
Jump to: navigation, search

Introduction

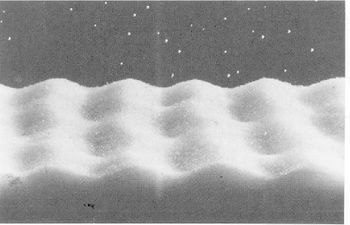
Figure 1. Ripples observed at Sea Rim State Park, along the coast of east Texas close to the border with Louisiana (courtesy by Zoltan Sylvester).

When a sandy seabed is subject to wave action and the wave orbital motion is strong enough to move sand grains, ripples often appear. The ripples induced by wave action are called “wave ripples”; their characteristics being different from those of the ripples generated by steady flows. The most striking difference between wave ripple fields and current ripple fields is the regularity of the former. Indeed, regular long-crested wave ripple fields are often observed on tidal beaches from which the sea has withdrawn at low water (see figure 1).

The characteristics of wave ripples are described in the accompanying article Wave ripples, which also explains their crucial importance for sand transport in the coastal zone (see also the articles Sand transport and Sediment transport formulas for the coastal environment).

The formation of wave ripple fields, characterized by well-defined wavelengths, is initiated by the interaction of seabed disturbances with the wave orbital motion. This article deals with the underlying processes giving rise to different wave ripple patterns.



The mechanism of ripple formation

Wave ripples form because the interaction of the oscillatory flow, induced by surface waves close to the bottom, with a bottom undulation of small amplitude generates steady streamings which consist of recirculating cells (see the flow visualizations of Kaneko and Honji[1]). Indeed the presence of the bottom waviness induces periodic spatial variations of the streamwise oscillatory velocity component. Hence the nonlinear self-interaction of the velocity field, that is due to the convective acceleration, generates time-independent terms into momentum equation which can be balanced only by the presence of a steady velocity component.

Figure 2. Steady streaming generated by an oscillatory flow over a wavy wall for [math]R_\delta=0.1[/math], [math]2 \pi \delta/\lambda=0.15[/math] being the dimensionless wavenumber of the bottom waviness (adapted from Blondeaux[2]). In the figure [math]x[/math] and [math]y[/math] are dimensioness spatial coordinates scaled with [math]\delta[/math].

The spatial distribution of this steady streaming depends on the parameters of the problem, namely, 1) the ratio [math]\eta/\lambda[/math] between the height [math]\eta[/math] and the length [math]\lambda[/math] of the bottom waviness, 2) the ratio [math]U_0/(\omega\lambda)[/math] between the amplitude [math]U_0/\omega[/math] of the fluid displacement oscillations and [math]\lambda[/math] ([math]U_0[/math] and [math]\omega[/math] denote the amplitude and angular frequency of the velocity oscillation of the fluid particles), 3) the ratio between [math]U_0/\omega[/math] and the conventional thickness [math]\delta=\sqrt{2 \nu/\omega}[/math] of the viscous bottom boundary layer (the reader should notice that [math]U_0/(\omega \delta)=U_0\delta/(2\nu)=R_\delta/2[/math], [math]R_\delta[/math] being the Reynolds number characteristic of the bottom boundary layer). As these parameters are varied, different balances take place into momentum equation among the local acceleration, the convective acceleration, the pressure gradient and the viscous terms. A discussion of the relative importance of these terms and of the different approches which are used to determine the flow field as function of the values of the parameters (see among others Lyne [3], Sleath [4], Blondeaux [2], Vittori [5]) can be found in Hara and Mei [6].

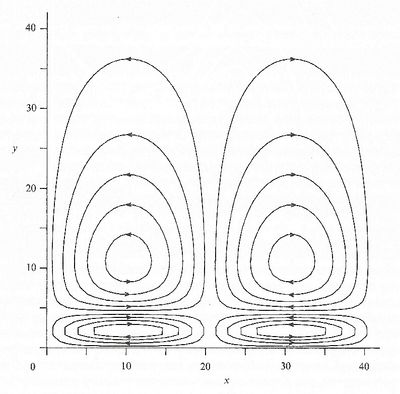
Figure 2 shows an example of the steady recirculating cells determined on the basis of Blondeaux's [2] analysis. When the steady velocity component close to the bed is directed from the troughs towards the crests of the bottom undulation and is strong enough to drag the sediments, the sediments tend to move from the troughs towards the crests. The tendency of sediments to pile up near the crests is opposed by the component of the gravity force acting in the down-slope direction. It follows that the growth of the amplitude of the bottom waviness is controlled by a balance between these two effects. If gravity prevails over drag, the amplitude decays, otherwise it grows leading to the appearance of ripples. Moreover, Sleath [4] argued that the effect is stronger for ripple wavelengths of the same order of magnitude as the amplitude of the fluid displacement oscillations since in this case particle settling locations will tend, after several cycles, to the nearest ripple crest. Once formed, ripples do not continue to grow indefinitely because the steady streaming is modified by nonlinear effects and, as the ripples get steeper, an equilibrium configuration is attained.


Models of ripple formation

Idealized models allow to predict the conditions leading to the appearance of ripples and some of their geometrical characteristics. Even though they are not straightforward to be used, it is worthwhile to introduce them and briefly summarize the results they provide. First of all, they show that the ripple wavelength and height do not depend on just one dimensionless parameter (this finding is also supported by some laboratory observations) and they suggest the most appropriate parameters to be used to improve the empirical predictors described in article Wave ripples.


Two-dimensional ripples

The formation of two-dimensional ripples can be investigated by determining the time development of a two-dimensional random perturbation of the sea bottom characterized by a small amplitude and subject to a harmonic oscillatory flow (see Stability models). The assumption of a small amplitude of the perturbation allows the hydrodynamic and morphodynamic problems to be linearized and solved by considering the time development of a generic sinusoidal component of the bottom waviness characterized by a wavenumber [math]\alpha=2 \pi /\lambda[/math] with [math]\lambda[/math] of order [math]\delta[/math].

[math]y= \eta (x,t) = A(t) e^{i \alpha x} + c.c. . \qquad(1)[/math]

To define the bottom profile (1), a Cartesian coordinate system is introduced with the origin located on the average bottom, the [math]y[/math]-axis vertical and pointing upwards and the [math]x[/math]-axis aligned in the direction of the fluid oscillations.

The hydrodynamic problem (the determination of the oscillatory flow over a wavy bed) was first solved by Sleath [4], who considered moderate values of the Reynolds number such that the flow regime is laminar and both small and large values of the ratio between the ripple wavelength and the fluid displacement oscillations. Later Blondeaux [2] solved the problem for fluid displacement oscillations of the same order of magnitude as the wavelength of the bottom waviness.

The time development of the bottom waviness can be evaluated by considering sediment continuity (Exner) equation, after the introduction of an appropriate sediment transport predictor which relates the sediment flux to the bottom shear stress. The linearized sediment continuity equation leads to

[math]\large\frac{d A}{dt}\normalsize= \gamma (t) A(t) , \qquad(2) [/math]

where [math]\gamma[/math] is a complex quantity ([math]\gamma=\gamma_r + i \gamma_i[/math]) (see Blondeaux[2]). The time average [math]\overline \gamma_r[/math] of [math]\gamma_r[/math] describes the growth/decay of the bottom waviness, depending on its positive/negative value and is named 'growth rate', while the time average [math]\overline \gamma_i[/math] of [math]\gamma_i[/math] is related to the migration speed of the bottom forms. The periodic parts of [math]\gamma[/math], characterized by a vanishing time average (namely [math]\gamma_r-\overline \gamma_r[/math] and [math]\gamma_i-\overline \gamma_i[/math]), turn out to be small and describe the vertical and horizontal oscillations of the bottom profile, around its average position, which take place during the wave cycle. If the small oscillations of the bottom profile around its averaged position are neglected, the bottom profile turns out to be described by

[math]\eta( x, t) = A_0 \exp \left[ \overline \gamma_r \tau \right] \exp \left[ i \alpha \left( x + \large\frac{ \overline \gamma_i}{\alpha}\normalsize \tau \right) \right] + c.c. , \qquad (3) [/math]

where [math]\tau=Q t[/math] is the morphodynamic temporal scale and the value of [math]Q[/math] depends on the formula used to quantify the sediment transport rate.

The analysis of Blondeaux [2] shows that, at the leading order of approximation, [math]\overline \gamma_i[/math] vanishes and the bottom forms do not migrate, because of the symmetry of the problem. On the other hand the growth rate [math]\overline \gamma_r[/math] of the bottom perturbation depends on the dimensionless parameters [math]R_\delta=U_0 \delta/\nu, R_p=\sqrt{\left( \rho_s/\rho-1\right) g d^3}/\nu, \psi_d=U_0^2/\left( \left( \rho_s/\rho-1\right) g d \right), s = \rho_s/\rho[/math] or their combinations, where [math]\rho_s[/math] and [math]\rho[/math] are the densities of the sediment particles and the fluid, respectively, [math]g[/math] is gravity acceleration and [math]d[/math] is the grain size. When [math]\overline{\gamma_r}[/math] is plotted as function of [math]\alpha[/math] for assigned values of the relative density [math]s[/math] and the flow and sediment Reynolds numbers, denoted by [math]R_\delta[/math] and [math]R_p[/math] respectively, the results of Blondeaux[2] show that a critical value [math]\psi_{d,crit}[/math] of [math]\psi_d[/math] exists such that for values of [math]\psi_d[/math] larger than the critical value, perturbation components characterized by wavenumbers falling within a restricted range have a positive growth rate and grow exponentially in time. Increasing values of [math]\psi_d[/math] lead to an increase of the range of unstable wavenumbers while decreasing values of [math]\psi_d[/math] make the unstable wavenumbers to collapse around a single value of the wavenumber ([math]\alpha_{crit}[/math]) named 'critical wavenumber'.

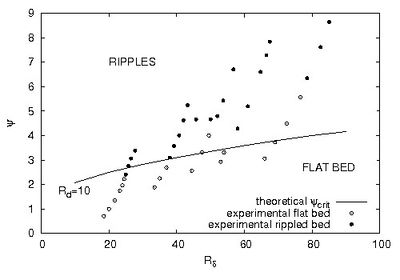
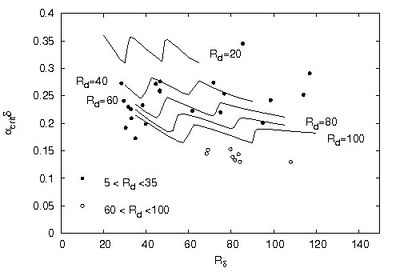
Figure 3. Region of existence of ripples and flat beds in the [math](\psi_d,R_\delta)[/math]-plane. Experimental observations for [math]5\lt R_d\lt 15[/math] and [math]s=2.65, \mu=0.15, n=0.4[/math] (adapted from Blondeaux[2]).

Figure 3 shows the regions of existence of ripples ([math]\psi_d \gt \psi_{d,crit}[/math]) and flat beds ([math]\psi_d \lt \psi_{d,crit}[/math]) in the [math](R_\delta,\psi_d)[/math]-plane, as predicted by the stability analysis, along with the experimental observations of Blondeaux et al.[7] who observed ripple formation using an oscillating tray apparatus.

Figure 4. Critical value [math]\alpha_{crit}[/math] of [math]\alpha[/math] plotted versus the flow Reynolds number [math]R_\delta[/math] for [math]s=2.65, \mu=0.15, n=0.4[/math] and different values of [math]R_d=R_p\sqrt{\psi_d}[/math].

As pointed out in the accompanying article Wave ripples, the dynamics of sediment grains and bed forms in oscillating trays is different from that forced by oscillatory flows in water tunnels or under sea waves. Indeed, although the fluid velocity distribution relative to axes fixed in the bed is the same, the forces acting on a sediment particle are not the same. This is because the force [math]\rho U_0 \omega V[/math] on a particle of volume [math]V[/math] due to the pressure gradient in an oscillatory flow is not equal to the inertia force [math]\rho_s U_0 \omega V[/math] on a similar particle in an oscillating tray. On the other hand, the force on the particle due to the shear stress is the same in both cases. However, the measurements of Zala Flores and Sleath [8] show that the movement of sediment grains is dominated by the shear stress and inertia plays a minor role when the parameter [math]\large\frac{U_0 \omega}{(s - 1) g}\normalsize \lt 0.1[/math] . The reader can easily verify that the data described in the following satisfy this condition. In figure 3, the theoretical values are obtained for [math]s=2.65[/math] and different values of [math]R_p[/math] such that [math]R_d=U_0d/\nu=R_p \sqrt{\psi_d}=10[/math], while the experimental observations are characterized by values of [math]R_d[/math] falling in the range [math](5,15)[/math].

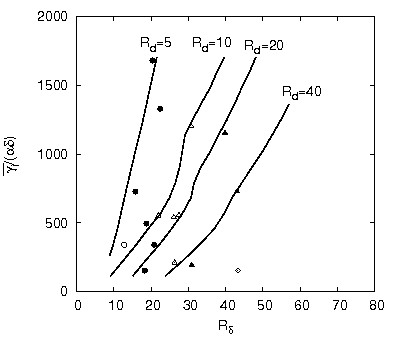
Notwithstanding the quantitative differences between the theoretical results and the experimental data, the stability analysis appears to provide a reliable description of the process which leads to ripple formation. Moreover, the model shows that coarser sediments, which are characterized by larger values of [math]R_p[/math], give rise to longer ripples. This theoretical finding is in agreement with laboratory measurements as shown in figure 4, where the critical values of [math]\alpha_{crit}[/math] are plotted versus the Reynolds number [math]R_\delta[/math] of the bottom boundary layer for different values of the sediment Reynolds number [math]R_d=R_p \sqrt{\psi_d}[/math].

The comparison between the theoretical values and the experimental measurements shows that the analysis underpredicts the observed wavelengths but a qualitative agreement with the laboratory measurements can be observed. Moreover, figure 3 shows that the ripple wavelength can not be predicted on the basis of just one parameter since both [math]R_\delta[/math] and [math]R_d[/math] affect the length of the bedforms.


Rolling-grain ripples and vortex ripples

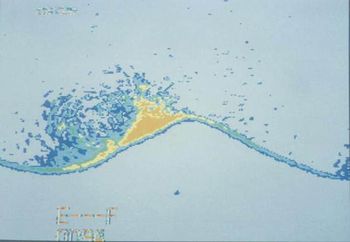
Figure 5. Visualization of the sediments picked-up from the bed and carried into suspension by the vortices shed at the crests of large amplitude ripples in an oscillatory flow (courtesy of Dr. Megale).

A linear approach, which considers ripples characterized by small (strictly infinitesimal) amplitudes, cannot follow the time development of the bottom forms for long times and determine their equilibrium amplitude. The prediction of the equilibrium amplitude of ripples is quite important since for large amplitudes the flow separates from the crests of the ripples and vortices are shed which modify the mechanism of sediment transport (see figure 5).

A model to determine the temporal growth of ripples for long times and to predict their equilibrium amplitude was developed by Vittori and Blondeaux[9] taking into account nonlinear effets but assuming that they are weak, i.e. when the amplitude of the ripples is moderate and the bottom boundary layer does not separate from the ripple crests.

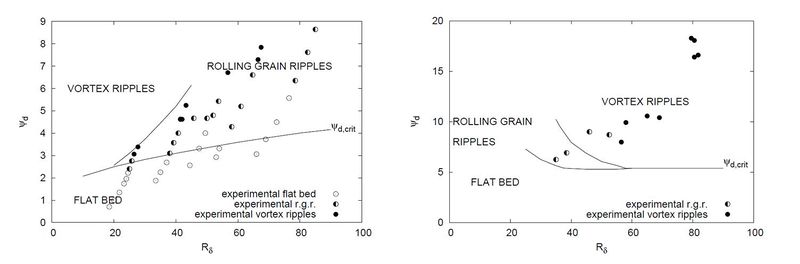
Figure 6a. Rolling-grain ripples (courtesy of John F.A. Sleath).
Figure 6b. Vortex ripples (courtesy of John F.A. Sleath).

Vittori and Blondeaux[9] showed that, for fixed values of [math]s[/math] and [math]R_p[/math], the plane [math](R_\delta,\psi_d)[/math] can be divided into three regions. In the first region, defined by values of [math]\psi_d[/math] smaller than [math]\psi_{d,crit}[/math], the flat bottom is stable and ripple do not appear. For values of [math]\psi_d[/math] larger than [math]\psi_{d,crit}[/math] the linear analysis of Blondeaux[2] predicts the formation of ripples. In this region, Vittori and Blondeaux[9] identified two sub-regions. In one sub-region the ratio between the predicted height and length of the ripples at equilibrium is smaller than about [math]0.1[/math] and the analysis, according with the criterion suggested by Sleath[10], predicts the appearance of rolling grain ripples as equilibrium bedforms (see figure 6a). In the other sub-region, the analysis shows that no equilibrium is possible assuming that nonlinear effects are weak. In this case the amplitude of the bottom forms grows and nonlinear effects become increasingly more important till the boundary layer separates from the ripple crests and vortex ripples are generated (see figure 6b).

A comparison between theoretical predictions and the experimental observations of Blondeaux et al. [7] and Horikawa and Watanabe[11] is shown in figure 7.

Figure 7. Regions in the [math](R_\delta,\psi_d)[/math]-plane where a flat bed, rolling-grain ripples, and vortex ripples are expected to appear according to Vittori and Blondeaux[9]. Comparison between the theoretical predictions and the laboratory observations. Left panel: [math]R_d=R_p\sqrt{\psi_d}=10, \beta=0.15, s=2.65[/math] and experimental data by Blondeaux et al. [7] ([math]5\lt R_d\lt 10[/math]); Right panel: [math]R_d=R_p\sqrt{\psi_d}=40, \beta=0.15, s=2.65[/math] and experimental data by Horikawa and Watanabe [11] ([math]30\lt R_d\lt 50[/math]).


Brick-pattern ripples

Figure 8. Brick-pattern ripples (courtesy of John F.A. Sleath).

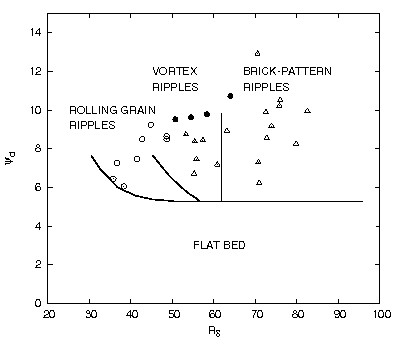
Vittori and Blondeaux[12] developed an idealized model for the formation of brick-pattern ripples (see figure 8) by considering the time development of a sandy bottom subject to an oscillatory flow when three-dimensional initial disturbances of the bottom profile are present. The analysis shows that brick-pattern ripples can be originated by the simultaneous growth of two-dimensional and three-dimensional components of the initial disturbance, which interact with a mechanism similar to that described by Craik[13] in a different context. The results allow to identify the regions in the parameter space where brick-pattern ripples appear.

In summary, on the basis of the analyses of Blondeaux[2], Vittori and Blondeaux[9] and Vittori and Blondeaux[12] the plane [math](R_\delta, \psi_d)[/math] (for fixed values of [math]s[/math] and [math]R_d[/math]) can be divided into four different regions where the stability analyses predict i) stable flat bed, ii) rolling-grain ripples, iii) vortex ripples, iv) brick-patterns ripples. Figure 9 shows the different regions in the [math](R_\delta,\psi_d)[/math]-plane for fixed values of [math]s[/math] and [math]R_d[/math] along with the experimental results of Sleath and Ellis[14] and Horikawa and Watanabe[11].

Figure 9. Limiting curves dividing the [math](R_\delta, \psi_d)[/math]-plane in regions where a flat bed, rolling grain ripples, two-dimensional vortex ripples, brick-pattern ripples are expected to form ([math]R_d=R_p\sqrt{\psi_d}=40, s=2.65, \beta= 0.15[/math]). Also shown are experimental data by Sleath and Ellis[14] and Horikawa and Watanabe[11] for [math]35 \lt R_\delta \lt 45[/math] (white points = rolling grain ripples, black points = vortex ripples, triangles = brick pattern ripples). Adapted from Vittori and Blondeaux[12].




Tile ripples

Field and experimental observations show the existence of hexagonal ripples, named tile ripples. Roos and Blondeaux[15] developed a model similar to that of Vittori and Blondeaux[12] but they considered the forcing flow generated by the simultaneous presence of two surface waves characterized by the same angular frequency but different amplitudes and directions of propagation, such as the wave field which can be observed when a wave is partially reflected by a coastal structure. In this case, close to the bottom, the irrotational flow is not unidirectional but characterized by an elliptical behaviour. The model of Roos and Blondeaux [15] predicts the conditions for the formation of tile ripples.








Models of ripple migration due to waves only

When a steady current is superimposed to surface waves, the so-called wave-current ripples are observed, the characteristics of which are somewhat between those of wave ripples, previously described, and those of current ripples. Since the flow, generated close to the bottom by sea waves, is characterized by an oscillatory velocity component and by a steady velocity component originated by nonlinear effects [16], the ripples generated by sea waves of large amplitude have geometrical and kinematical characteristics which are similar to those of the ripples generated by the interaction between waves and currents.

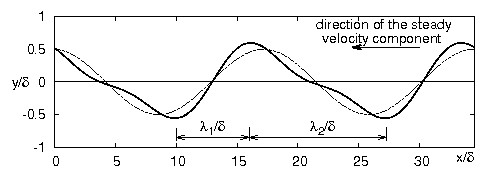
Figure 10. Equilibrium profile of the ripples predicted by the stability analysis of Blondeaux et al. [17] for [math]R_\delta=15, R_d= 25, \large\frac{\sqrt{\psi_d}-\sqrt{\psi_{dc}}}{\sqrt{\psi_{dc}}}\normalsize = 0.1, 2 \pi \delta/\lambda= 0.364, \delta/L = 0.004[/math] (continuous line, considering [math]O(\delta/L)[/math]-effects; broken line, neglecting [math]O(\delta/L)[/math]-effects). The ratio between the ripple height [math]\eta[/math] and the ripple wavelength [math]\lambda[/math] is abount [math]0.067[/math].

The distinguishing geometric characteristic of the ripples generated by large amplitude waves is the asymmetry of their profile (see figure 10).

Moreover, the presence of a steady streaming induces the migration of the bottom forms. Blondeaux et al. [18] investigated whether the steady velocity component has a destabilizing or a stabilizing effect on the formation of ripples. Moreover, they determined the migration speed of the ripples. This information is of practical interest since it is common practice to evaluate the average sediment transport rate from measurements of ripple migration assuming that the sediment transport rate is related to the migration speed times the height of the ripples [19].

When nonlinear effects due to large amplitude sea waves are taken into account to determine the forcing flow, the value of [math]\gamma[/math] turns out to have both a real [math]\gamma_r[/math] part and imaginary [math]\gamma_i[/math] part. The value of [math]\overline \gamma_r[/math] differs from that determined by Blondeaux[2] because of terms of order [math]a/L[/math] and the migration speed of the bottom forms is proportional to the steepness of the surface wave ([math]a[/math] and [math]L[/math] denote the amplitude and the length of the sea waves). A discussion of the results of the linear analysis can be found in Blondeaux et al. [18], where the interested reader can also find an exhaustive discussion of the influence of second order terms in the wave slope on the stability of the sea bottom.

Figure 11 shows a comparison between the migration speed predicted by the theoretical analysis and that measured by Blondeaux et al. [18] during laboratory experiments.

Figure 11. Theoretical and experimental values of the dimensioless migration speed of ripples plotted versus [math]R_\delta[/math]. The theoretical values are obtained by evaluating the sediment transport rate by means of Hallermeier's formula [20] and the migration speed is scaled introducing the morphodynamic time scale [math]\tau[/math] [18]. The experimental measurements are for [math]5\lt R_d\lt 10[/math] (white circles), [math]10\lt R_d \lt 15[/math] (black circles), [math]15 \lt R_d \lt 20[/math] (white triangles), [math]20 \lt R_d\lt 25[/math] (black triangles), [math]25 \lt R_d \lt 30 [/math] (while diamond).
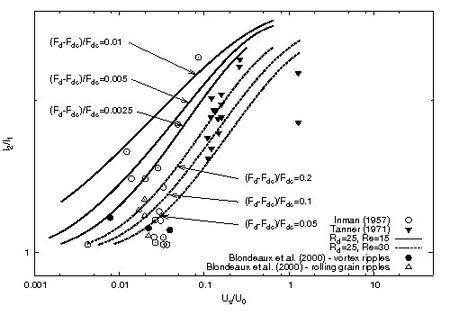
Figure 12. Theoretical value of the symmetry index plotted versus [math]U_s/U_0[/math], where the value of [math]U_s/U_0[/math] for a monochromatic wave is assumed to be [math]3 \pi \delta R_\delta/(4L) [/math]. [math]R_d = 25[/math] and [math]R_\delta = 15,30[/math] are values characteristic of Blondeaux et al.'sCite error: Invalid <ref> tag; refs with no name must have content (2000) experiments. The experimental data of Inman[21], Tanner[22], Blondeaux et al. [18] are also shown. The values of [math]\psi_d[/math] are related to [math]F_d[/math] by [math]\psi_d=F_d^2[/math].


















The analysis of Blondeaux et al. [18] neglects the nonlinear effects related to the amplitude of the bottom forms. Hence, the bottom profile turns out to be sinusoidal and its amplitude can not be determined. To describe the process, which shapes the bottom profile giving rise to bottom forms characterized by crests sharper than the troughs and up-current slopes smaller than the down-current slopes, Blondeaux et al. [17] considered the interaction of the bottom perturbation with itself.

Figure 10 shows the equilibrium profile of a ripple obtained by means of the theory, for fixed values of the parameters along with that obtained neglecting [math]O(a/L)[/math] effects. The characteristic profile of ripples affected by a steady streaming can be recognized from the lee side of the ripple being steeper than the stoss side. The steady velocity component in figure 10 is from the right to the left. In this case the ratio [math]\lambda_2/\lambda_1[/math] turns out to be [math]1.81[/math]. The experimental data by Inman[21], Tanner[22], who used sand, and those described in Blondeaux et al. [18], who used high density plastic particles, show that the symmetry index increases as the ratio between the steady velocity component and the amplitude of the oscillating one increases but a limiting value exists. The same dependence is observed in the theoretical results presented in figure 12. Interestingly, for strong steady currents, the different curves tend to converge towards a common value that appears to be the maximum value of the symmetry index and ranges between [math]2[/math] and [math]3[/math]. A quantitative comparison between experimental observations and theoretical findings can be made looking at table 1, which shows the values of [math]\lambda_2/\lambda_1[/math] detected during experiments nr. 39, 40, 42 of Blondeaux et al. [18] along with the theoretical values computed for the same parameters of the problem.

Table 1. Experimental and theoretical values of [math]\lambda_2/\lambda_1[/math] for the experiments of Blondeaux et al. [18] characterized by the presence of rolling grain ripples.
exp. nr. [math](\lambda_2/\lambda_1)_{exp.}[/math] [math](\lambda_2/\lambda_1)_{theor.}[/math]
39 1.19 1.17
40 1.23 1.17
42 1.30 1.20


For experiments nr. 30, 35, 36, 41, the theory predicts the formation of vortex ripples and hence the symmetry index can not be computed.


Ripple formation: the turbulent boundary layer case

Figure 13. Ratio between the amplitude [math]U_0/\omega[/math] of the fluid displacement oscillations and the wavelength [math]\lambda[/math] of the ripples plotted versus the parameter [math]\rho d/(\rho_s-\rho) g T^2[/math]. The continuous lines are the theoretical predictions of the linear stability anaysis of Foti and Blondeaux[23] developed assuming the flow regime to be turbulent. 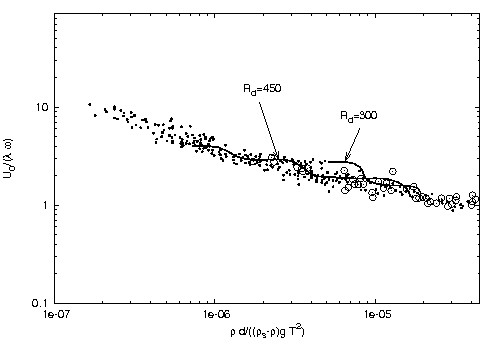The experimental data of Manohar[24] (points) and Sleath[4] (open circles) are taken from the book of SleathCite error: Invalid <ref> tag; refs with no name must have content (adapted from Foti and Blondeaux[23]).

The analyses previously summarized explain the appearance of ripples and predict their characteristics at incipient formation but for moderate values of the Reynolds number, such that the flow regime is laminar. For field conditions, the Reynolds number [math]R_\delta[/math] is often larger than its critical value and the flow regime is turbulent. The model of Blondeaux (1990) was extended to the turbulent regime by Foti and Blondeaux[23] who considered the Reynolds averaged momentum equations and used a simple turbulence model. They evaluated, in particular, the Reynolds stresses by using a constant turbulent eddy viscosity [math]\nu_T[/math]. In order to obtain a reasonable velocity profile, as suggested by Sleath[25] and by Engelund and Fredsøe[26] in another context, they further replaced the no-slip condition at the bottom by a partial slip condition. Figure 13 shows a comparison between laboratory data and the theoretical predictions made by means of this model.







Vortex ripples

Figure 14. Vorticity contours of the oscillatory flow over a wavy wall [math]R_\delta=50, \eta/\lambda=0.15, U_0/(\omega \lambda)=0.75[/math] (The vorticity isolines are [math]0.15 U_0/\omega[/math] apart, thick lines = clockwise vorticity, thin lines = counter-clockwise vorticity). Panel a) [math]\omega t = \pi/2[/math]; Panel b) [math]\omega t = \pi[/math]; Panel c) [math]\omega t =5 \pi/4[/math]; Panel d) [math]\omega t = 3 \pi/2[/math]; Panel e) [math]\omega t = 2 \pi[/math]. Adapted from Blondeaux and Vittori[27].

The models based on linear and weakly nonlinear stability analyses are no longer valid when the parameters of the problem are far from the critical conditions. In this case, nonlinear effects become relevant and a perturbation approach can be used no longer. Under these circumstances, only numerical simulations of momentum and Exner equations can be used to determine the fluid flow and the time development of the bottom forms.

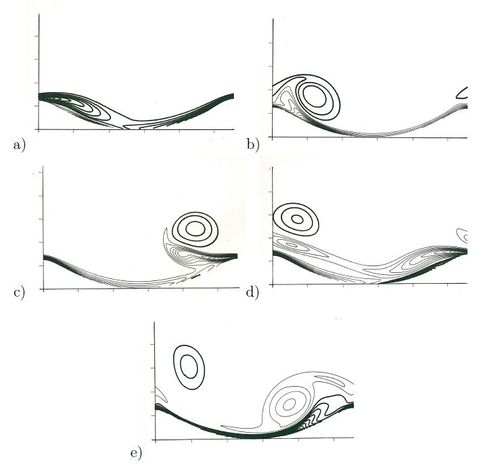
The oscillatory flow over vortex ripples was first determined by the numerical integration of momentum equation by Shum[28] and Blondeaux and Vittori[27]. Figure 14 shows the spanwise component of vorticity over two-dimensional vortex ripples at different phases from the beginning of the numerical simulation, as computed by the latter authors. When the fluid moves from the left to the right, clockwise vorticity is generated along the bottom profile and tends to roll up and to generate a well defined vortex (figure 14a,b).

As the external fluid velocity reverses its direction, the clockwise vortex is no longer fed but it is convected from the right to the left by the external flow (figure 14c,d). Simultaneously, counter-clockwise vorticity is shed from the crest and the phenomenon repeats similarly during the following half cycle (figure 14e). Of course, the size, the strength and the number of vortex structures generated by the oscillatory flow over a rippled bed depends on the parameters of the problem. In particular, these first simultations considered moderate values of the Reynolds number such that the flow regime can be assumed to be laminar.

Figure 15. Time evolution of the crests of the ripples generated by the growth of a sandy Gaussian hump which interacts with an oscillatory flow characterized by [math]U_0=0.26[/math] m/s, [math]T=6[/math] s, [math]d=0.3[/math] mm (adapted from Marieu et al. [29].

Nowadays, the power of computers is such as to allow the evaluation of the turbulent flow field by means of Direct Numerical Simulations (DNS) of Navier-Stokes and continuity equations or using Large Eddy Simulations (LES) (Scandura et al. [30], Barr and Slinn[31], Zedler and Street[32], Chalmoukis and Dimas[33], Leftheriotis and Dimas[34]). However, for practical applications, it is convenient to compute the turbulent oscillatory flow over vortex ripples by using the Reynolds averaged equations and a turbulence model.

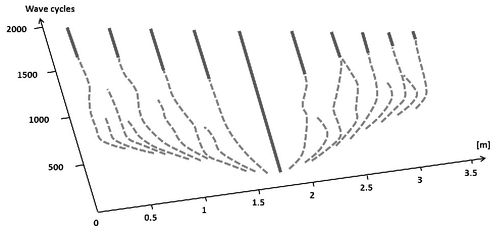
Andersen[35] was one of the first to couple the evaluation of the turbulent flow by means of a RANS approach with the evaluation of the time development of the bottom profile computed by means of Exner equation. More recently, Marieu et al. [29] used a similar approach to simulate ripple growth from a quasi-flat bed. Turbulence closure was achieved by means of the model of Wilcox[36] while the sediment transport rate took into account both the bed load contribution and the suspended load contribution. Moreover, the morphology module simulated the avalanches that take place at the crests of the ripples when the steepness of the profile becomes too large. Figure 15 shows the time development of the position of the crests of the ripples generated by the interaction of an oscillatory flow with a Gaussian hump located at the middle of the computational domain, It clearly appears that further ripples are generated around the initial hump. Later these ripples are characterized by a complex nonlinear dynamics; they migrate, split, merge, annihiliate and they eventually attain an equilibrium configuration.


Related articles

Wave ripples
Stability models
Rhythmic shoreline features
Principles of spontaneous bedform generation
Sand ridges in shelf seas
Beach Cusps
Nearshore sandbars
Bedforms and roughness
Sand transport
Sediment transport formulas for the coastal environment


References

  1. ↑ Kaneko A. and Honji H. (1979.) Double structures of steady streaming in the oscillatory viscous flow over a wavy wall. J. Fluid Mech. 93, 727-736.
  2. ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 Blondeaux P. (1990). Sand ripples under sea waves. Part 1. Ripple formation. J. Fluid Mech. 218, 1-17.
  3. ↑ Lyne W.H. (1971). Unsteady viscous flow over a wavy wall. J. Fluid Mech. 50, 33-48.
  4. ↑ 4.0 4.1 4.2 4.3 Sleath J.F.A. (1976). On rolling-grain ripples. J. Hydraul. Res. 14, 69-81.
  5. ↑ Vittori G. (1989). Non-linear viscous oscillatory flow over a small amplitude wavy wall J. Hydraulic Research 27 (2), 267-280.
  6. ↑ HaraT. and Mei C.C. (1990). Oscillating flows over periodic ripples. J. Fluid Mech. 211, 183-209.
  7. ↑ 7.0 7.1 7.2 Blondeaux P., Sleath J.F.A. and Vittori G. (1988). Experimental data on sand ripples in an oscillatory flow. Rep. 01/88. Inst. of Hydraulics, University of Genoa.
  8. ↑ Zala Flores N. and Sleath J.F.A. (1998). Mobile layer in oscillatory sheet flow. J. Geophys. Res. 103 (N. C6) 12783-12793.
  9. ↑ 9.0 9.1 9.2 9.3 9.4 Vittori G., Blondeaux P. (1990). Sand ripples under sea waves. Part 2. Finite amplitude development. J. Fluid Mech. 218, 19-39.
  10. ↑ Sleath J.F.A. (1984) Sea bed mechanics. John Wiley and Sons.
  11. ↑ 11.0 11.1 11.2 11.3 Horikawa K. and Watanabe, A. (1968). Laboratory study on oscillatory boundary layer flow. Proc. 11th Coastal Eng. Conf., 467-486.
  12. ↑ 12.0 12.1 12.2 12.3 Vittori G., Blondeaux P. (1992). Sand ripples under sea waves. Part 3. Brick-pattern ripple formation. J. Fluid Mech. 239, 23-45.
  13. ↑ Craik A.D.D. (1971). Nonlinear resonant instability in boundary layers. J. Fluid Mech. 50, 393-413.
  14. ↑ 14.0 14.1 Sleath J.F.A. and Ellis A.C. (1978). Ripple geometry in oscillatory flow. Univ. Cambridge Dept. Engr. Rept. A/Hydraulics TR2, 15 pp.
  15. ↑ 15.0 15.1 Roos P.C., Blondeaux P. (2001). Sand ripples under sea waves. Part 4. Tile ripple formation. J. Fluid Mech. 447, 227-246.
  16. ↑ Longuet-Higgins M.S. (1953). Mass transport in water waves. Philos. Trans. R. Soc. 345. 535-581.
  17. ↑ 17.0 17.1 Blondeaux P., Foti E., Vittori G. (2015). A theoretical model of asymmetry wave ripples. Phil. Trans. R. Soc. A 373 (2033). pii: 20140112. doi: 10.1098/rsta.2014.0112.
  18. ↑ 18.0 18.1 18.2 18.3 18.4 18.5 18.6 18.7 18.8 Blondeaux P., Foti E., Vittori G. (2000). Migrating sea ripples. European Journal of Mechanics - B/Fluids 19 (2), 285-301.
  19. ↑ Fredsøe J. and Deigaard R. (1992). Mechanics of coastal sediment transport. Advances Series on Ocean Engineering 3 World Scientific.
  20. ↑ Hallermeier R.J. (1982). Oscillatory bedload transport: data review and simple formulation. Continental Shelf Res. 1, 159-190.
  21. ↑ 21.0 21.1 Inman D.L. (1957). Tech. Mem. U.S. Beach Erosion N. 100.
  22. ↑ 22.0 22.1 Tanner W.F. (1971). Numerical estimates of ancient waves, water depth and fetch. Sedimentology 16, 71-88.
  23. ↑ 23.0 23.1 23.2 Foti E., Blondeaux P. (1995). Sea ripple formation: the turbulent boundary layer case. Coastal Eng., 25 (3-4), 227-236.
  24. ↑ Manohar M. (1955) 'Mechanics of bottom sediment movement due to wave action', Tech. Memo. 75, 121 pp., U.S. Army Corps of Eng., Beach Erosion Board, Washington, D.C.
  25. ↑ Sleath J.F.A. (1991). Velocities and shear stresses in wave-current flows. J. Geophys. Res. 96(C8), 15237-15244.
  26. ↑ Engelund F. and Fredsøe J. (1982). Sediment ripples and dunes. Ann. Rev. Fluid Mech. 14, 13-37.
  27. ↑ 27.0 27.1 Blondeaux P., Vittori G. (1991). Vorticity dynamics in an oscillatory flow over a rippled bed. J. Fluid. Mech. 226, 257-289.
  28. ↑ Shum K.T. (1988) A numerical study of vortex dynamics over rigid ripples. PhD Thesis M.I.T. Dep. of Civil Engineering, Cambridge, Mass.
  29. ↑ 29.0 29.1 Marieu V., Bonneton P., Foster D.L. and Ardhuin F. (2008). Modeling of vortex ripple morphodynamics. J. Geophys. Res. 113 (C09007), 1-15.
  30. ↑ Scandura P., Vittori G. and Blondeaux P. (2000). Three-dimensional oscillatory flow over steep ripples. J. Fluid Mech. 412, 355-378.
  31. ↑ Barr B. and Slinn, D. (2004). Numerical simulation of turbulent, oscillatory flow over sand ripples. J. Geophys. Res., 109 (C9), 1-19.
  32. ↑ Zedler E.A. and Street R.L. (2006). Sediment transport over ripples in oscillatory flow. J. Hydraul. Eng. A.S.C.E. 132 (2), 1-14
  33. ↑ Chalmoukis I.A. and Dimas A.A. (2016). Numerical simulation of oscillatory flow over 3-D vortex ripples using the Immersed Boundary Method. 26th Int. Ocean and Polar Eng. Conf., 26 June-2 July, Rhodes, Greece. ISOPE-I-16-549.
  34. ↑ Leftheriotis G. and Dimas A. (2016). Large Eddy Simulation of oscillatory flow and mor- phodynamics over ripples. Proc. 35th Conference on Coastal Engineering, Antalya, Turkey, 2016.
  35. ↑ Andersen K.H. (1999). The dynamics of ripples beneath surface waves and topics in shell models of turbulence. PhD thesis, Det Naturvidens-kabelige Fakultet Københavns Universitet.
  36. ↑ Wilcox D.C. (1988). Re-assessment of the scale-determining equation for advanced turbulence models. AIAA Journal 26 (11), 1299-1310.


The main authors of this article are Paolo Blondeaux and Giovanna Vittori
Please note that others may also have edited the contents of this article.
Citation: Paolo Blondeaux; Giovanna Vittori; (2024): Wave ripple formation. Available from http://www.coastalwiki.org/wiki/Wave_ripple_formation [accessed on 30-12-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Wave_ripple_formation&oldid=81127"