Waves
There is typically a distinction between short waves, which are waves with periods less than approximately 20 s, and long waves or long period oscillations, which are oscillations with periods between 20-30 s and 40 min. Water-level oscillations with periods or recurrence intervals larger than around 1 hour, such as astronomical tide and storm surge, are referred to as water-level variations. The short waves are wind waves and swell, whereas long waves are divided into surf beats, harbor resonance, seiche and tsunamis. Natural waves can be viewed as a wave field consisting of a large number of single wave components each characterised by a wave height, a wave period and a propagation direction. Wave fields with many different wave periods and heights are called irregular.
Contents
Wave classifications
Sea waves can be classified in different ways, depending on the parameters considered [1]. Considering the parameter [math]r=h/L[/math], the ratio of water depth [math]h [/math] and wavelength [math]L[/math], a commonly used classification is[2]:
| [math]r[/math] | < 0.05 | 0.05 – 0.5 | > 0.5 |
|---|---|---|---|
| classification | shallow water or long wave | intermediate water wave | deep water or short wave |
Considering the wave period [math]T[/math], waves can be classified as in the table below[3]:
| period | wave type | generation mechanism |
|---|---|---|
| [math]\boldsymbol{T \lt 0.1 s}[/math] | Capillary waves | Generated by wind and restored by surface tension |
| [math]\boldsymbol{0.1 \lt T \lt 1 s}[/math] | Ultra-gravity waves (0.1 s < T < 1 s) | Generated by wind and restored by surface tension and gravity |
| [math]\boldsymbol{1 \lt T \lt 30 s}[/math] | Gravity waves | Generated by wind and restored by gravity |
| [math]\boldsymbol{30 s \lt T \lt 5 min}[/math] | Infra-gravity waves | Caused by wind and atmospheric pressure gradients and restored by gravity |
| [math]\boldsymbol{5 min \lt T \lt 12 h}[/math] | Long-period waves (seiches, storm surges, tsunamis | Caused by atmospheric pressure gradients and earthquake and restored by gravity |
| [math]\boldsymbol{12 h \lt T \lt 24 h}[/math] | Ordinary tidal waves | Due to the gravitational attraction of celestial bodies (moon and sun) and restored by gravity and Coriolis force |
| [math]\boldsymbol{T \gt 24 h}[/math] | Trans-tidal waves | Due to storms and gravitational attraction and restored by gravity and Coriolis force |
In oceanography, the term “sea state” is used to indicate the temporary (about a half-hour) and local significant wave height [math]H_s[/math] of the sea surface (with respect to wind waves and swell) as a consequence of wind interaction. The World Meteorological Organization (WMO) defines the sea states according to the Douglas Sea Scale of the table below:
| [math]\boldsymbol{H_s}[/math] [m] | < 0.1 | 0.1 – 0.5 | 0.5 – 1.25 | 1.25 – 2.5 | 2.5 - 4 | 4 - 6 | 6 - 9 | 9 – 14 | > 14 |
|---|---|---|---|---|---|---|---|---|---|
| classification | calm (glassy) | smooth (wavelets) | slight | moderate | rough | very rough | high | very high | phenomenal |
Short Waves
Types of short waves
[4]Short waves are waves, generated by the wind that propagate towards the beach. They can be either actively forced by the wind (wind waves - see below) or they can have left their generation area (swell waves - see below). Incident waves are the primary source of energy input to the beach. On their way from deep water towards the shoreline they undergo refraction and shoaling processes. In deep water, incident waves are nearly sinusoidal; as they propagate into shallower water (shoaling), their celerity and wavelength decrease and as the total energy flux should remain constant (according to linear theory and neglecting bottom friction), the wave height must increase while the wavelength decreases.
[4]As the waves propagate towards the shoreline, the wave shape becomes increasingly skewed with peaked wave crests and longer, rounded wave troughs, and wave orbital velocities become larger under crests than under troughs. This is a characteristic of fundamental importance to sediment transport, especially seaward of the wave breakpoint as there will be a tendency for the incident waves to push sediment towards the beach, see Shoreface profile.
The short waves are the single most important parameter in coastal morphology. Wave conditions vary considerably from site to site, depending mainly on the wind climate and on the type of water area. The short waves are divided into:
- Wind waves, also called storm waves, or sea. These are waves generated and influenced by the local wind field. Wind waves are normally relatively steep (high and short) and are often both irregular and directional, for which reason it is difficult to distinguish defined wave fronts. The waves are also referred to as short-crested. Wind waves tend to be destructive for the coastal profile because they generate an offshore (as opposed to onshore) movement of sediments, which results in a generally flat shoreface and a steep foreshore.
- Swell are waves, which have been generated by wind fields far away and have travelled long distances over deep water away from the wind field, which generated the waves. Their direction of propagation is thus not necessarily the same as the local wind direction. Swell waves are often relatively long, of moderate height, regular and unidirectional. Swell waves tend to build up the coastal profile to a steep shoreface.
Wave breaking
[4]Depth-limited wave breaking is the prerequisite for the generation of nearshore currents and secondary wave phenomena. Seaward of the surf zone, any wave energy losses primarily occur through whitecapping and friction against the sea bed. As the waves approach the beach, however, depth-limited breaking will occur when orbital velocities, increasing towards the beach exceed the wave phase speed which decreases in the landward direction. The breaking wave height, [math]H_b[/math] is related to the water depth at breaking, [math]h_b[/math], through
[math]H_b = \gamma \, h_b ,[/math]
where [math]\gamma[/math] is the breaker index. In nature waves are irregular and random and using [math]H_{rms}[/math] as the measure of wave height, the maximum time-averaged value of the breaker index ([math]\lt \gamma_{rms}\gt [/math]) is in the range 0.35-0.8 , see Breaker index.
The predominant type of wave breaking depends on wave steepness and beach slope expressed through the surf scaling parameter:
[math]\epsilon = \pi H / T g \tan^2 \beta , [/math]
where [math]T[/math] is wave period, [math]g[/math] is the acceleration of gravity and [math]\tan \beta[/math] is the beach slope. With spilling breakers, [math]\epsilon \gt 20[/math], plunging occurs for [math]2.5 \lt \epsilon \lt 20[/math] and surging breakers predominate when [math]\epsilon \lt 2.5[/math].
As waves propagate towards the beach, short wave energy is gradually lost through breaking and long infragravity waves become more important.
For a more detailed introduction the reader is referred to the article Shallow-water wave theory.
Wave generation
Wind waves are generated as a result of the action of the wind on the surface of the water. The wave height, wave period, propagation direction and duration of the wave field at a certain location depend on:
- The wind field (speed, direction and duration)
- The fetch of the wind field (meteorological fetch) or the water area (geographical fetch)
- The water depth over the wave generation area.
Swell is, as previously stated, wind waves generated elsewhere but transformed as they propagate away from the generation area. The dissipation processes, such as wave-breaking, attenuate the short period much more than the long period components. This process acts as a filter, whereby the resulting long-crested swell will consist of relatively long (wavelength) waves with moderate wave height.
Wave transformation
The types of transformation discussed here are mainly related to wave phenomena occurring in the natural environment. When the waves approach the shoreline, they are affected by the seabed through processes such as refraction, shoaling, bottom friction and wave breaking. However, wave breaking also occurs in deep water when the waves are too steep. If the waves meet major structures or abrupt changes in the coastline, they will be transformed by diffraction. If waves meet a submerged reef or structure, they will overtop the reef – see Wave transformation.
Statistical description of wave parameters
Because of the random nature of natural waves, a statistical description of the waves is normally always used. The individual wave heights often follow the Rayleigh-distribution. Statistical wave parameters are calculated based on this distribution. The most commonly used variables in coastal engineering are described in this section – see Statistical description of wave parameters.
Wave climate classification according to wind climate
The different wind climates, which dominate different oceans and regions, cause correspondingly characteristic wave climates. These characteristic wave climates can be classified as follows:
- Storm wave climate.
- Swell climate.
- Monsoon wave climate.
- Tropical cyclone climate.
For details on these classifications follow the link Wave climate classification according to wind climate.
Long Waves
The long waves are primarily second order phenomena of shallow water wave processes. The four main types of long waves are described in the following.
Surf beat
Natural waves often show a tendency to wave grouping, where a series of high waves follows a series of low waves. This is especially pronounced on open sea-coasts, where the incoming waves may be of different origins and will thus have a large spreading in wave heights, wave directions, and wave periods (or frequencies). Wave grouping will cause oscillations in the wave set-up with a period corresponding to approx. 6 – 8 times the mean wave period; this phenomenon is called surf-beats (sea also Infragravity waves). Surf-beats near port entrances are very important in relation to mooring conditions in the port basins and sedimentation in the port entrance.
Harbour resonance
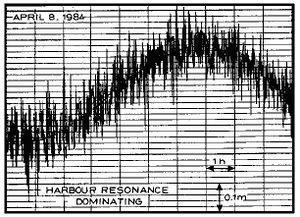
Harbour resonance is the forced resonant oscillation of a semi-confined water body (e.g. a harbour basin or a lagoon) connected to a larger water body (the sea). If long-period oscillations are present in the sea, e.g. due to seiches, large oscillations at the natural frequency of the semi-confined water body may occur. Oscillations at the first harmonic, which are the simplest mode of resonance, are often called the pumping or Helmholz mode. See also harbour seiches induced by infragravity waves.
Harbour resonance normally has periods in the range of 2 to 10 minutes. It is especially important in connection with the mooring conditions of large vessels, as their resonance period for the so-called surge motion is often close to that of the harbour resonance. In addition, the associated water exchange may cause siltation. It is important to establish whether seiches do occur in an area through field investigations, and if so, to take it into account in the layout of the port. If seiches do occur, they will inevitably penetrate the entrance. However, the impact on the port may be minimised through a proper layout.
Lake seiche
A lake seiche is the free oscillation of a water body, caused by rapid variations in the wind conditions. Seiches can occur in closed water areas, such as lakes or lagoons, and in semi-closed water bodies, such as bays. The period of the seiche oscillation is typically in the range of 2 to 40 minutes.
Tsunami
Tsunamis are long waves caused by a strong local disturbance of the water mass, for example by seismic events. Tsunamis generally consist of a few successive waves with wavelengths typically much larger than the wavelength of wind-generated waves and much smaller than the wavelength of tidal waves. Tsunamis travel very fast in the deep oceans. If the water depth is 5000 m, the speed will be more than 200 m/s or about 800 km/hour. A tsunami is normally not very high in deep water, but when it approaches the coastline, the wave will be shoaling and can reach a height of more than 10 m. Tsunamis are rare and coastal projects seldom take them into account. However, in very sensitive projects, such as nuclear power plants located in the coastal hinterland, the risk must be considered. For further details see the article Tsunami.
[4]Infragravity waves
Infragravity waves are waves that are forced by difference interactions in the incident wave frequency band and consequently they have frequencies which are lower than the frequencies of incident waves ~0.005-0.05 Hz. From a morphodynamic viewpoint, much of the interest in infragravity waves is due to the fact that they are often standing in the cross-shore direction and sometimes also alongshore, therefore resulting in a stationary drift velocity field in the bottom boundary layer. They can therefore potentially provide a mechanism for nearshore bar formation and the generation of three-dimensional features such as rip currents and rhythmic bars. Apart from quasi-steady drift velocities in the boundary layer, orbital velocities associated with these motions can generate oscillatory sediment fluxes which have been demonstrated to be important to the net sediment transport in the surf zone.
Nearshore-standing infragravity waves may occur as either leaky mode waves which are two-dimensional standing waves having a succession of antinodes and nodes away from the point of reflection (e.g. the shoreline), or as edge waves which are three-dimensional waves trapped against the nearshore by reflection and refraction and which can propagate alongshore (progressive edge waves) or be longshore-standing (standing edge waves). Edge waves have a finite number of nodes/antinodes in the cross-shore direction (the number of cross-shore surface elevation nodes is called the mode number, [math]n[/math]), and a theoretically infinite number of nodes/antinodes in the longshore dimension.
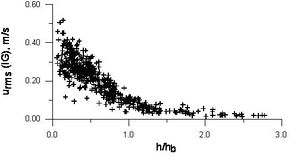
Infragravity wave heights and orbital velocities increase towards the shoreline (see Fig. 5. below), while incident wave heights decrease landward due to wave breaking. Infragravity waves should therefore be of increasing relative importance with proximity to the shoreline and sediment resuspension and transport become increasingly affected by infragravity motions. A more comprehensive treatment of nearshore infragravity waves can be found in e.g. Aagaard and Masselink (1999)[5] and Infragravity waves.
Measurement of Waves
Waves are traditionally measured with wave rider buoys. More recently, remote sensing techniques for measuring waves have been developed, see Measuring waves and currents by X-band radar.
Related articles
- Shallow-water wave theory
- Statistical description of wave parameters
- Infragravity waves
- Tsunami
- Seiche
- Wave set-up
- Wave transformation
- Breaker index
- Swash zone dynamics
References
- ↑ Curto, D., Franzitta, V. and Guercio, A. 2021. SeaWave Energy. A Review of the Current Technologies and Perspectives. Energies 14, 6604
- ↑ Cornett, A. 2008. A global wave energy resource assessment. In: Proceedings of the 18th International Offshore and Polar Engineering Conference, Vancouver, BC, Canada, 6–11 July 2008; ISOPE-2008-TPC-579, pp. 1–9
- ↑ Toffoli, A. and Bitner-Gregersen, E.M. 2017. Types of Ocean Surface Waves, Wave Classification. Encycl. Marit. Offshore Eng. 2017: 1–8
- ↑ 4.0 4.1 4.2 4.3 Written by Aagard, Troels. 2007.
- ↑ Aagaard, T. and Masselink, G., 1999. The Surf Zone. In: A.D.Short (ed) Handbook of Beach and Shoreface Morphodynamics, Wiley Interscience, pp.72-118.
Further reading
Mangor, K., Drønen, N. K., Kaergaard, K.H. and Kristensen, N.E. 2017. Shoreline management guidelines. DHI https://www.dhigroup.com/marine-water/ebook-shoreline-management-guidelines.
Please note that others may also have edited the contents of this article.
|