Physical processes and morphology of synchronous estuaries
Definition of Synchronous estuary:
A ‘synchronous estuary’ is where the sea surface slope due to the axial gradient in phase of tidal elevation significantly exceeds the gradient from changes in tidal amplitude. Many estuaries can be considered 'synchronous', according to this definition.
This is the common definition for Synchronous estuary, other definitions can be discussed in the article
|
Contents
Abstract
Estuaries are where 'fresh' river water and saline sea water mix. They act as both sinks and sources for sediments - of marine, fluvial, internal and atmospheric origin. Following the end of the last ice-age, retreating ice cover and the related rise in mean sea level resulted in receding coastlines. Large post-glacial melt-water flows gouged deep channels with the rate of subsequent in-filling dependent on localised availability of sediments. More recently, de-forestation and subsequent changes in farming practices substantially changed the patterns of river flows and both the quantity and nature of fluvial sediments. Thus present-day estuarine morphologies reflect adjustments to these longer-term, larger-scale effects alongside more recent, localised impacts from tectonic re-bound, urban development and engineering 'interventions‘.
Recently developed theories, describing tidal dynamics, salinity intrusion, sediment mechanics and their associated links with morphology have been shown to be broadly accurate in applications to 96 UK estuaries. The success in explaining existing morphologies in terms of the forcing parameters of tidal amplitude, [math]Z[/math], and river flow, [math]Q[/math], is summarised in Figures 8 and 9. Whilst individual estuaries exhibit localised features (related to underlying geology, flora and fauna, historical development and human intervention), the overall values of depth and length are shown, in these Figures to be consistent with the theories described in Sections 2 and 3.
In Section 4, these theories are used to estimate likely effects from projected changes in both mean sea level and river flows linked to future global climate change scenarios. Impacts from a rise in mean sea level of 1 m are shown to have negligible effects on tidal current amplitudes in deeper waters. By contrast, in depths less than 5 m, a 1 m rise in mean sea level can increase current amplitudes by more than 5 per cent. A 25 per cent increase in river flows produces (approximately) a 10% increase in estuarine depths, breadths and lengths - similar in magnitude to a 0.5 m increase in mean sea level. A full description of all of the associated theoretical developments is beyond the present scope. Hence, having adopted a descriptive (rather than deductive) approach, only three references are cited; these should provide gateways to the fuller theoretical developments.
Challenge
Ports and cities have developed on almost all major estuaries, exploiting opportunities for both inland and coastal navigation, alongside supplies of freshwater and fisheries. More recently, the scale of inland navigation has generally declined and the historic benefit of an estuary counterbalanced by growing fears of flooding. Since estuaries often supported major industrial development, remobilisation of contaminants can threaten ecological diversity and recreational use.
Over the next century, rising sea levels at cities bordering estuaries may require major investment in flood protection or even relocation of strategic facilities. The immediate questions concern the changing magnitudes of tides, surges and waves. However, the underlying longer term (decadal) issue is how estuarine bathymetries will adjust with consequent impacts on these dynamics (Figure 1).
Here we address the following questions:
What determines estuarine shape, length and depth? How will estuaries adapt to Global Climate Change?
The emphasis here is on meso- and macro-tidal estuaries (i.e. tidal amplitudes at the mouth greater than 1 metre) using observed data mainly drawn from the UK.
Range of UK estuaries
Figure 2 shows the 96 estuaries of England and Wales, values were derived for: Mean depth, [math]D[/math]; Mean width (at the mouth), [math]B[/math]; Mean lateral slope, [math]\tan \alpha[/math]; tidal intrusion length, [math]L[/math]; Mean tidal amplitude (at the mouth), [math]Z[/math]; Mean river flow, [math]Q[/math].
Morphological Types
Descriptions of the three most common estuarine types in England and Wales (Figure 2) follow.
Rias are short, deep and steep-sided with small river flows
Coastal Plain estuaries are long and funnel-shaped with gently sloping triangular cross-sections providing extensive inter-tidal zones;
Bar Built estuaries are short and shallow with small values of both river flow and tidal range. Sandy estuaries tend to be short, whilst muddy estuaries tend to be long. In sedimentary terms, Bar Built estuaries are located along coasts with plentiful supplies of marine sediments and, consequently, are close to present-day equilibrium. Coastal Plain estuaries are continuing to infill following ‘over-deepening’ via post-glacial river flows, while Rias are drowned river valleys (with related cross-sections) as a consequence of (relative) sea level rise. The mean discharge of the world's largest river, the Amazon, is 200,000 m3/s, representing 20 per cent of net freshwater flow. Moreover, the cumulative discharge of the next nine largest rivers amounts to a similar total. Outside of these 10 largest rivers, Q < 15,000 m3/s. Annual daily maxima for UK estuaries typically ranging from 10 to 600 m3/s . Mean flows are generally close to 1/20 of these maximum values. Hence, mean flows in UK estuaries typically range from 0.5 to 30 m3/s. Thus, estimates of the minimum flows for continuous estuarine functioning of approximately 1 m3/s correspond reasonably with the minimum mean flow for UK estuaries.
| Tidal amplitude | Mean river flow | Depth | Tidal length | Breadth | Lateral (side) slope | |
|---|---|---|---|---|---|---|
| UK estuaries | [math]Z [m][/math] | [math]Q [m^3/s][/math] | [math]D [m][/math] | [math]L [km][/math] | [math]B [m][/math] | [math]\tan \alpha[/math] |
| All - mean | 1.8 | 14.9 | 6.5 | 20 | 970 | 0.013 |
| All – min (10th perc) | 1.20 | 0.2 | 2.5 | 5 | 130 | 0.004 |
| All – max (90th perc) | 2.6 | 35.9 | 17.3 | 41 | 3,800 | 0.129 |
| Ria | 1.7 | 6.3 | 9.3 | 12 | 490 | 0.037 |
| Coastal plain | 2.0 | 17.9 | 8.1 | 33 | 1,500 | 0.011 |
| Bar-built | 1.6 | 9.5 | 3.6 | 9 | 510 | 0.014 |
Governing processes
Processes involved in estuarine morphology include tides, surges, waves, currents, temperature, salinity, turbidity, ice, sediment transport, and a range of biological and chemical components. Tides, surges and waves are generally the major sources of energy input into estuaries. Pronounced seasonal cycles often occur in: temperature, light, waves, river flows, stratification, nutrients, oxygen and plankton. Estuarine morphology is often a balance between these continuous seasonal cycles, slow long-term processes (mean sea level rise), and extreme episodic events such as tsunamis and glacial melt-water.
The latest numerical models can accurately predict the immediate impact on tidal elevations and currents of changes in: bathymetry (following dredging or reclamation), river flow or bed roughness (linked to surficial sediments or flora and fauna). Likewise, such models can provide estimates of the variations in salinity distributions (ebb to flood, spring to neap tides, flood to drought river flows), though with a reduced level of accuracy. The further step of predicting longer-term sediment redistributions remains problematic. Against a background of subtly changing chemical and biological mediation of estuarine environments, specific difficulties arise in prescribing: available sources of sediment, rates of erosion and deposition, the dynamics of suspension and interactions between mixed sediment types.
The spectrum of tidal energy input is effectively constrained within a few tidal constituents and, in mid-latitudes, the lunar M2 constituent is generally greater than the sum of all others - providing a convenient basis for linearisation of the equations for tidal propagation. However, ‘mixing’ involves a wider-spectrum of interacting non-linear processes and is thus more difficult to simulate. The ‘decay-time’ for tidal, surge, wave and associated turbulent energy in estuaries is usually measured in hours. By contrast, the flushing time for river inputs generally extends over days.
Tides, surges and waves
The tides seen in estuaries are generated in ocean basins, analytical theories describe their subsequent propagation into estuaries and explain how and why tidal elevations and currents vary within estuaries. Non-linear aspects of estuarine propagation result in energy transfer from the semi-diurnal and diurnal constituents of ocean tides into additional higher harmonics. As tides and storm surges propagate into estuaries, in some systems they are amplified and in others rapidly diminished. Even within the same estuary, longer-period tidal constituents typically show little amplification, while shorter period higher harmonics are often significantly increased. Analytical solutions for a range of estuarine shapes and sizes indicate how these varying responses are influenced by: shape, length, bed friction and river flow. These solutions show that quarter-wavelength resonance is generally restricted to exceptionally long estuaries. See also Ocean and shelf tides.
Like tides, surges propagate as shallow water waves, raising sea levels along coasts to the right of propagation (Northern Hemisphere). Flooding often involves not only large but ‘peculiar’ surges. Rapid increases of sea level on time scales of hours can cause severe flooding in low lying coastal regions and dramatic loss of life. Rapid decreases in sea level can cause problems in the safe navigation of large vessels in shallow water.
Storm surge generation is via two forces: wind stress and the horizontal gradient of atmospheric pressure at the sea surface. The wind effect depends on water depth and increases in importance as the depth decreases, whereas the pressure effect is independent of depth. The most important mechanism for surge generation is wind stress acting over shallow water. Surges are, therefore, large and dangerous where storms impact on large areas of shallow Continental Shelves.
By contrast with tides and surges, surface wind waves have wavelengths which, except on beaches, are small in comparison with the water depth. They are generated by winds, which produce waves with a spectrum of frequencies and magnitudes depending on the distance over which the wind acts, i.e. ‘fetch'. Ocean-generated waves travel very large distances and are known as 'swell'. In shoaling water, the wave orbital velocities reach the seabed and their propagation slows, causing refraction and dissipation of energy by bottom friction. Wave energy is also dissipated in deep water by white capping and ultimately by breaking at the shore. Wave conditions at the coast therefore depend on fetch, wind duration, exposure to incoming swell, and (local) bathymetry. Very shallow water dissipates wave energy and so often reduces extreme wave heights within estuaries.
Stratification and salinity intrusion
Noting the earlier definition of estuaries as regions where salt and fresh water mix, here we examine the details of this mixing. The predominance of mixing by vertical stirring driven via tidally-induced turbulence has long been recognised. More recently, the importance of incorporating the effects of tidal straining and resultant convective overturning has been recognised. On Neap tides, near-bed saline intrusion may enhance stability while on Springs, enhanced near-surface advection of sea water can lead to overturning. Saline intrusion undergoes simultaneous adjustments in axial location and mixing length - explaining traditional problems in understanding observed variations over spring-neap and flood-drought conditions. See also: Seawater intrusion and mixing in estuaries.
The ratio of currents, [math]U_0/U[/math], associated respectively with river flow and tides, can be shown to be the most direct determinant of stratification in estuaries
In strongly tidal estuaries, saline intrusion has little impact on tidal propagation. Conversely, the nature of saline intrusion is overwhelmingly determined by the combination of tidal motions alongside the flow of river water. The pattern of intrusion may be altered by ‘interventions’ such as dredging, barrier construction or flow regulation alongside impacts from changes in mean sea level or river flows linked to Global Climate Change.
Sedimentary processes
Figure 3 shows the basic processes that control sediment movement in most estuaries. The predominant influences are generally erosion and advection via tidal and storm currents, enhanced in exposed shallow water by wave stirring. Leading questions are:
What causes trapping, sorting and high concentrations of suspended sediments? How does the balance of ebb and flood sediment fluxes adjust to maintain bathymetric stability?
Conventionally, erosion is assumed to occur when the bed shear forces exceed the resistance of the bed sediment, characterised by a ‘critical shear stress for erosion‘. In nature, this threshold depends on particle size distribution and both chemical and biological modulation, including effects of bio-turbation and biological binding. Bioturbation of the top metre or so of surface sediment may significantly reduce erosion thresholds. Conversely, (surface) biological binding can have the opposite effect - especially in inter-tidal zones. Erosion depends, not only on the prevailing physical, chemical and biological composition, but on corresponding conditions at (and since) the time of deposition. Subsequent settlement of particles depends on their size, density and the ambient regime of turbulence and chemical forces in the surrounding water. See also: Sediment deposition and erosion processes.
Bed roughness strongly influences erosion and deposition rates, it is largely determined by the composition (fine to coarse) and form (ripples, waves) of the bed. Bed roughness can change significantly over both the ebb to flood and neap to spring tidal cycles. Associated erosion and deposition rates may then vary considerably over these cycles and dramatically over seasons or in the course of a major event.
Suspended sediments exhibit extreme variability, with sizes ranging from fine to coarse and particle diameters ranging from clay <4 μ, silt < 60 μ, sand < 1000 μ, to gravels. In higher concentrations, silt and clay tend to flocculate into multiple assemblages which can both settle more rapidly and inhibit the upward flux of turbulent energy from the sea bed. Moreover, once deposited, consolidation of cohesive material can radically change re-erosion rates. Only a few percent of 'mud' content may strongly influence a seemingly cohesionless sandy bed.
Analytical solutions encapsulate and integrate the processes of erosion, suspension and deposition to provide descriptions of the magnitude, time-series and vertical structure of sediment concentrations. These descriptions enable the complete range of sediment regimes to be characterised in terms of varying sediment type, tidal current speed and water depth, (Figure 4).

By assuming that eddy diffusivity [math]K_z[/math] and eddy viscosity [math]E[/math] can be approximated by [math]K_z =E=fUD[/math], analytical solutions indicate how the essential scaling of sediment motion is synthesised in the dimensionless parameter [math]E/W_sD[/math], where [math]f[/math] is the bed friction coefficient, [math]D[/math] is water depth, [math]U[/math] tidal current amplitude and [math]W_s[/math] sediment fall-velocity. Turbulent diffusion, parameterized by the coefficient [math]E[/math], promotes the suspension of particles by random vertical oscillations, whereas the fall velocity [math]W_s[/math] represents steady advective settlement. The time taken for a particle to mix vertically by dispersion is [math]D^2/E[/math] whereas settlement by vertical advection occurs within [math]D/ W_s[/math]. Thus the ratio of [math]E / W_s D[/math] reflects the relative times of deposition by advective settlement to diffusive vertical excursions. The significance of this parameter is illustrated by the simulated time-series of suspended sediment shown in Figure 4. As [math]E \to W_s D[/math], the mean time in suspension approaches a maximum and hence both mean concentration and net transport will increase. Typically, this condition occurs for [math]W_s \sim 1 mm/s[/math] , i.e. particle diameter [math]d \sim 30 \mu m[/math].
Spring-Neap Cycle
In the absence of significant residual currents, the erosional time series for an M2 - S2 dominated tidal regime will show pronounced components at M4, MS4, MSf, and Z0 fre-quencies. These latter components are generated by nonlinear combinations of M2 and S2 currents and not by any (usually small) tidal current amplitudes at these emergent frequencies. For all but the coarsest grain sediment, several cycles of ebb and flood movement may occur between erosion and subsequent deposition. Hence, deposition can occur over a wide region beyond the source. Since time in suspension increases for finer, slowly settling material, such mechanisms may contribute to a residue of fine materials on tidal flats and to trapping of coarser material in deeper channels. Over a spring-neap tidal cycle, the peak in suspended sediment concentration for finer sediments will generally occur 2-3 days after the occurrence of maximum tidal currents.
Observed time-series
Suspended concentrations of fine sediments in tidal estuaries typically range from 100 to more than 1000 mg/l, whereas concentrations in shelf seas are invariably less than 10 mg/l. Moreover, observational and numerical modelling studies indicate only a small fraction of the net tidal flux of sediments is permanently deposited.
Figure 5 shows three examples of simultaneous time series recordings of suspended sediment and tidal velocity. These examples were selected as illustrative of tidally dominated conditions and correspond to tranquil weather conditions. The Dover Strait is a highly (tidally) energetic zone, 30 km wide and up to 60 m deep, linking the North Sea to the English Channel with currents exceeding 1 m/s. The Mersey Estuary is a shallow (<20 m deep) estuary with tidal range up to 10 m; the measurements shown were taken in the narrow entrance channel, 1 km wide, 10 km long. The Holderness measurements were taken some 4 km offshore of a long rapidly eroding coastline (glacial till).
In all three cases the fortnightly, MSf, constituent is largest. The spectral peak in the sediment distribution in the Dover Strait corresponds to a settling velocity of 10-4 m/s. The Mersey and Holderness are likely to contain more coarse-grained sediments. The mean concentration in the Mersey is an order of magnitude higher than in the Dover Strait.
Explaining existing morphology
Established estuarine classification systems for: tidal elevation, vertical current structure, salinity intrusion and stratification enable estuarine responses to be linked to forcing factors. For ‘Synchronous Estuaries’, newer analytical solutions extend these dynamical responses to encompass sedimentary regimes and stable bathymetry.

Assumptions
Owing to the complexity of estuaries, it is necessary to make certain assumptions in order to be able to provide analytical solutions for the diverse range of dynamic interactions and mixing processes.
(1) Consideration of a single predominant tidal constituent – the principal lunar semi-diurnal constituent, M2 - this provides the basis for linearisation of dynamical equations. Contributions to higher tidal harmonics (M4, M6, ..) are left out of consideration.
(2) Linearisation of the quadratic bed friction formulae, which is valid for the strongly tidal estuaries of the UK.
(3) The coefficients of eddy viscosity and diffusivity are assumed to be vertically and temporally constant with magnitudes proportional to a product of the bed friction coefficient, tidal velocity amplitude and water depth. These approximations are generally valid in strongly tidal, shallow, well mixed estuaries;
(4) The use of ‘Synchronous Estuary’ solutions.
It is further assumed that the estuarine cross-section can be represented by a triangular shape with constant uniform slope [math]\tan \alpha[/math] (i.e. cross-section [math]D^2/\tan \alpha[/math]). Width [math]D[/math] and breadth [math]B[/math] vary along the estuarine axis as [math]D=D_0 (x/L)^n, \; B=B_0 (x/L)^n[/math], where [math]x[/math] the distance from the estuarine head, [math]L[/math] is the length of tidal influence, [math]n \approx 0.8[/math].
Synchronous estuaries: length, breadth and depth
Synchronous solutions
By introducing the assumption of a Synchronous Estuary, explicit expressions can be derived for the amplitude, [math]U[/math], and phase, [math]\theta[/math], of tidal currents, alongside the tidal length, [math]L[/math], of an estuary in terms of the tidal elevation amplitude, [math]Z[/math], water depth , [math]D[/math], and bed friction coefficient, [math]f[/math] and [math]S_L[/math] bed slope.
[math]U=Z \ g \ k \ /\sqrt{\omega^2+F^2} \qquad (1) [/math]
[math]\tan \theta = - F/\omega=2 \ S_L \ / (D_0 k) \qquad (2) [/math]
[math]k=\omega / \sqrt{0.5 g D_0} \qquad (3) [/math]
[math]L=\large\frac{4D_0^{5/4}}{5Z^{1/2}} \frac{(2g)^{1/4}}{(1.33 f \omega)^{1/2}}\normalsize \approx 2460 \large\frac{D_0^{5/4}}{Z^{1/2}}[/math] for [math]f=0.0025 \qquad (4) [/math]
with the linearised bed friction coefficient, [math]F=1.33 f U/D [/math]. The adoption of this ‘synchronous’ assumption enables an analytical emulator to be formulated, incorporating tidal dynamics, saline intrusion, and sediment mechanics. This emulator provides explicit expressions for saline intrusion length, [math]L_I[/math],
[math]L_I=0.005 \large\frac{D_0^2}{f U U_0} \qquad (5) [/math]
where [math]U_0[/math] is the river flow velocity and [math]D_0[/math] depth at the mouth. The emulator suggests that bathymetric stability is maintained via a combination of tidal dynamics and ‘delayed’ settlement of sediments in suspension and can be used to derive conditions necessary to maintain zero net flux of sediments, i.e. bathymetric stability.
The depth at the mouth, [math]D_0[/math], can be derived from an empirical relationship for the salt intrusion length. This relationship can be expressed in terms of river discharge [math]Q[/math] as
[math]D_0= \ 12.8 \ (Q \tan \alpha)^{0.4} \qquad (6) [/math]
assuming a triangular cross section with side slopes, [math]\tan \alpha[/math]. A comparison of theory and observations for UK estuaries is shown in Figures 7 and 8. This expression is independent of both tidal elevation amplitude, [math]Z[/math] and bed friction coefficient, [math]f[/math]. The observed and theoretical bathymetric envelope shown in Figure 10 support the conclusion that the river flow velocity, [math]U_0[/math], within the saline intrusion zone, can be given in mixed estuaries by:
[math]U_0 = \sqrt{D_0} / 333 \; m/s \qquad (7) [/math]
and is invariably of the order of 1 cm/s for [math]2 \lt D_0 \lt 50m[/math] (for UK estuaries). Combining the above expressions for length, [math]L[/math], and depth at the mouth, [math]D_0[/math] gives
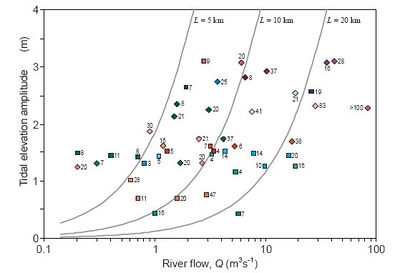
[math]L = 2980 \ \sqrt{Q \tan \alpha / Z f } \qquad (8) [/math].
This estimate is compared with observations in Figure 9.
| Type | [math]D_0 \sim A Q^p[/math] | [math]L \sim A Q^p[/math] | [math]B \sim A Q^p[/math] |
|---|---|---|---|
| ALL | A=3.3 p=0.47 (0.55) | A=3.0 p=0.68 (0.64) | A=98 p=0.86 (0.75) |
| Ria | A=5.1 p=0.31 (0.74) | A=3.1 p=0.74 (0.93) | A=41 p=1.05 (0.80) |
| Coastal plain | A=3.0 p=0.38 (0.67) | A=6.7 p=0.64 (0.89) | A=106 p=0.85 (0.71) |
| Bar built | A=2.4 p=0.38 (0.72) | A=9.2 p=1.37 (0.21) | A=11 p=1.37 (0.50) |
| Theory2 | A=2.3 p=0.4 | A=5.8 p=0.5 |
Statistical fits
Table 2 provides statistical fits between depth, [math]D_0[/math], tidal length, [math]L[/math] and breadth, [math]B[/math] with mean river flow, [math]Q[/math]. The correlation coefficients are given in parentheses. The theoretical values were calculated using a side slope, [math]\tan \alpha=0.013[/math] (the mean value calculated for all estuaries taken from Table 1).
The fits between depth, [math]D_0[/math], and river flow, [math]Q[/math], show powers of [math]Q[/math] of 0.31, for Ria estuaries, and 0.38 for both Coastal Plain and Bar Built estuaries. These values are all close to the theoretical value of 0.4 (from Eq. 6 for a triangular cross section). Likewise, the related values for the coefficient, [math]A[/math], are close to the theory except for Ria estuaries, where the higher coefficient reflects their greater depths. The fits between length, [math]L[/math], and river flow, [math]Q[/math], show an overall power of 0.68 for [math]Q[/math]. This is somewhat larger than the theoretical value of 0.5 and (partly in consequence) the value of the coefficient, [math]A[/math], is smaller. The fit for Coastal Plain estuaries is closest to the theoretical values. Overall we note statistically significant relationships (given by the [math]R^2[/math] values in parentheses in Table 2) between all of these parameters in all types of estuaries, indicating the tendency for morphologies to be confined within restricted parameter ranges. In addition, there is good agreement between typological classifications and statistical fits for the sizes and shapes of estuaries classified as either Coastal Plain or Bar Built.
Synchronous estuaries : bathymetric zone
A ‘Bathymetric Zone’ for mixed estuaries was derived, shown in Figure 10, enveloped by the conditions
(1) [math]L_I /L \lt 1[/math];
(2) [math]E_x/L \lt 1[/math] (where [math]E_x[/math] is the tidal excursion length); and
(3) the Simpson-Hunter criterion for vertical mixing ([math]D/U^3\lt 50 m^{-2}s^3[/math]).
By encapsulating the results in typological frameworks, the characteristics of any specific estuary can be compared against these theories and in a perspective of other estuaries. Identification of ’anomalous’ estuaries can provide insight into ‘peculiar’ conditions and highlight enhanced sensitivity to change. Discrepancies between observed and theoretical estuarine depths can be used to estimate the ‘age’ of estuaries based on the intervening rates of sea level rise.
Importantly, the new dynamical theories for estuarine bathymetry take no account of the sediment regimes in estuaries. Hence the success of these theories provoke a reversal of the customary assumption that bathymetries are determined by their prevailing sediment regimes. Conversely, it is suggested that the prevailing sediment regimes are in fact the consequence of rather than the determinant for estuarine bathymetries.
Sediment import, export, sorting and morphological stability
The ‘synchronous estuary’ solutions for tidal dynamics and salinity intrusion are extended to include erosion, suspension and deposition of sediments, see Figure 11. Integrating all of these processes into an ‘analytical emulator’ yields explicit expressions for concentrations and cross-sectional fluxes of sediments, This allows conditions consistent with zero net flux of sediments to be identified alongside their sensitivity to tidal range, particle size, bed friction coefficient and bathymetry. It is shown how the exchange of sediments switches from export towards import as the ratio of tidal amplitude to depth increases and as sediment size decreases. Thus, quantitative explanations are provided for the trapping, sorting and high concentrations of sediments in estuaries.
Stable Morphology
Within regions where tidal influences predominate, the ratio of sediment import (IM) to export (EX) is given by:
[math]\frac{IM}{EX} = \large\frac{r}{3}\normalsize \tan \theta = 0.37 \large\left( \frac{f U^2}{W_s} \right)^2 \qquad (9) [/math]
where [math]r = \omega / a [/math]; with [math]a[/math] the exponential decay rate of sediments in suspension.
Zero net flux then corresponds to:
[math]W_s = 0.61 f U \sim 0.0015 U \qquad (10) [/math].
The distribution for mean sediment concentration may be approximated by inserting this value of [math]W_s[/math],
[math]C = \gamma \rho f U^2 / D \alpha = \gamma \rho U (1+a^2) \qquad (11) [/math].
The conditions derived for maintaining stable bathymetry extend earlier concepts of flood and ebb-dominated regimes. Interestingly, these derived conditions correspond with maximum sediment suspensions. Moreover, the associated sediment fall velocities are in close agreement with settling rates observed in many estuaries. Figure 12 encapsulates these results, illustrating the dependency on delayed settlement (characterised by the half-life in suspension [math]t_{50}[/math]) and the phase difference, [math]\theta[/math], between tidal current and elevation. A feedback mechanism between tidal dynamics and net sedimentation/erosion is identified involving an interaction between suspended and deposited sediments.

Figure 12 illustrates how the balance between net import or export varies for: depths from 4 to 16m; fall velocities of 0.0001, 0.001 and 0.01 m/s tidal amplitudes from 1 to 4m (representative of neap to spring tidal variations).
Separate components from tidal non-linearities, involving [math]\cos \theta[/math] and [math]\sin \theta[/math] (where [math]\theta[/math] is the phase difference between tidal elevation [math]\zeta(t)[/math] and current [math]U(t)[/math], determine the balance between import and export. Combinations of [math]\theta[/math] and [math]t_{50}[/math] corresponding to zero net flux of sediments can be determined. It is found that for zero net flux, [math]W_s \sim f U[/math] . This latter relationship coincides with values of [math]K_z/ W_s D[/math] (the basic scaling parameter characterising suspended sediments), in the range 0.1 to 2. It appears that this is close to conditions corresponding to maximum suspended sediment concentrations.
Proceeding upstream from deep to shallow water, the balance between import of fine sediments and export of coarser ones becomes finer, i.e. selective ‘sorting’ and trapping. Likewise, more imports, extending to a coarser fraction, occur on spring than on neap tides. However, as more fine sediments are trapped, the effective value of f decreases, resulting in a tendency to increase estuarine length. The consequent more energetic dynamics will tend to increase depths and introduce coarser sediments. Hence some equilibrium will prevail, governed by the balance between the type and quantity of (marine) sediment supply.

Figure 13 indicates typical values of:
(i) effective fall velocities for morphological equilibria,
(ii) depth and time-averaged suspended sediment concentrations,
(iii) flushing times.
The observed results shown in Figure 13 are representative of observed settlement of fine sediments in a wide range of European estuaries. These studies indicated that settling was primarily via the formation of micro and macro-flocs, invariably close to the range suggested by the present theory.
The curves for fall velocity, [math]W_s[/math], and concentration, [math]C[/math], align directly with those for tidal current amplitude, [math]U[/math] (not shown here). This typology illustrates why many estuaries show high levels of fine suspended sediments. The results for [math]W_s[/math] suggest a narrow range of fall velocities, typically between 1 and 3 mm/s.
Likewise, the order of magnitude of observed suspended sediment concentrations is in good agreement with theoretical values. Figure 13 also shows loci of representative flushing times, [math]t_f[/math]. For river-borne dissolved or suspended sediments, the indicated values generally lie between 2 and 10 days (for residual current [math]U_0[/math] = 1 cm/s). These values are consistent with the range indicated from observations. Flushing times greater than the principal semi-diurnal tidal period (12.42h) provide valuable longer-term persistence of marine-derived nutrients, while flushing times less than the 15-day spring-neap cycle yield effective flushing of contaminants. Hence, there might be some ecological advantage to the bathymetric envelope defined by these two flushing times.
Impacts from changes in mean sea level and river flow
Using the above theories, estimates of likely impacts of Global Climate Change are quantified across a range of estuaries.
Explaining existing morphologies was seen as pre-requisite to forecasting future changes. Section 3 showed how bathymetries are dependent on a combination of tidal amplitude [math]Z [/math]and river flow [math]Q[/math]. In addition to the direct dynamical-sedimentary relationships, the response to mean sea level changes includes the problem of how the coastline and estuaries re-adjust within the local coastal and topographical conditions.
Morphological adjustment rates are generally slow and thus, existing bathymetries reflect some intermediate adjustment between antecedent formative conditions and a present-day dynamic equilibrium. This adjustment rate depends on both the supply of sediments for deposition and the ‘hardness’ of the geology for erosion. Annual volume changes of UK estuaries are typically of order 1% or less. Thus, even where conditions favour net import or export of a certain sediment fraction, limited marine supply (fluvial supply is generally much smaller in UK estuaries) or resistance to erosion can severely delay morphological adjustments.
Mean sea level
Over millennia, the inter-glacial rise and fall of sea level determines estuarine morphology. Following the end of the last ice-age, retreating ice cover and the related rise in mean sea level (transgression) have resulted in receding coastlines and consequent major changes in both the dynamics and morphology of estuaries. Sea levels rose globally by about 150m between 20k and 5k BP, followed by a ‘still stand’ with changes in mean sea level of less than a few metres.
Over the Holocene, the rate of rise has been controlled by isostatic rebound (the rise of land masses that were depressed by the huge weight of ice sheets during the last glacial period). A hinge line at about 550 N across the UK separates ‘falling’ sea level to the north from rising in the south - reflecting the varying rates of isostatic rebound. Over the last century, sea levels have risen between 10 and 20 cm, while forecasted rises for the next century range between 10 and 100 cm. If sea level rise accelerates with climate change, there could be a switch from a predominately stable shoreline to much more active regression.

A Vulnerability Index for tidal currents [math]U[/math] is shown in Figure 14. The values of depth and tidal amplitude ([math]D[/math] and [math]Z[/math]) are intended to represent values at the mouth of an estuary but can also be applied to upstream regions (away from the extreme tidal limit). The Figure has, superposed in red dashed contours, percentage impacts on [math]U[/math] resulting from an increase in sea level of 1 m.
As shown in Eq 1 current amplitude, U can be represented by:
[math]U \propto Z^{1/2} \ D^{1/4} \ f^{-1/2} [/math] (in shallow water), and
[math]U \propto Z D^{-1/2} [/math] (in deep water, where depth is more than 10 times the tidal elevation amplitude, [math]Z[/math]).
The zero impact contour corresponds to conditions for maximum values of tidal current amplitude, which occur when [math]D \sim 5 + 10 Z [/math]. In deeper water little sensitivity is shown, whereas in depths less than 5 m, increases in tidal current amplitude greater than 5 per cent occur.
Changes in Morphology
Likely changes to depth, length and breadth ([math]D_0[/math], [math]L[/math] and [math]B[/math]) for a rise in mean sea level of 0.5 m and changes in river flow, [math]Q[/math], of +/- 25 per cent are shown, for UK estuaries, in Table 3. Using the formulae shown above for Synchronous Estuaries, inserting these changes in river flow, [math]Q[/math], and the resulting changes in depth, [math]\delta D[/math], we can estimate the changes in length, [math]\delta L[/math]. Likewise, the changes in breadth, [math]\delta B[/math], associated with the changes in depth, [math]\delta D[/math] can be estimated by assuming the side-slope gradients, [math]\tan \alpha[/math], are unchanged. Table 3 provides quantitative indications of the resultant changes for the estuarine data sets shown in Figure 2. Overall we anticipate, due to the 25 per cent variation in river flow, changes in:
- estuarine lengths of the order of 0.5 to 5 km and
- breadths of the order 50 to 250 m.
Corresponding changes due a rise in mean sea level of 50 cm are: increases in tidal length of the order 1 to 2.5 km and breadths of 70 to 100 m
| Estuary | [math]D_0[/math] | [math]\delta D_Q[/math] | [math]L[/math] | [math]\delta L_Q[/math] | [math]\delta L_{msl}[/math] | [math]B[/math] | [math]\delta B_Q[/math] | [math]\delta B_{msl}[/math] |
|---|---|---|---|---|---|---|---|---|
| Type | [m] | +/- | [km] | +/- | + | [m] | +/- | + |
| All minimum | 2.5 | 0.25 | 5 | 0.62 | 1.28 | 130 | 38 | |
| All mean | 6.5 | 0.65 | 20 | 2.5 | 1.94 | 970 | 100 | 77 |
| All maximum | 17.3 | 1.73 | 41 | 5.12 | 1.49 | 3800 | 266 | |
| Coastal plain | 8.1 | 0.81 | 33 | 4.12 | 2.57 | 1500 | 147 | 91 |
List of symbols
[math]B \qquad[/math] channel breadth
[math]C \qquad [/math] sediment concentration in suspension
[math]D \qquad [/math] water depth
[math]D_0 \qquad [/math] depth at mouth
[math]E \qquad [/math] eddy viscosity
[math]E_x \qquad [/math] tidal excursion length
[math]f \qquad [/math] bed friction coefficient ([math]\sim[/math]0.0025)
[math]F \qquad [/math] linearised bed friction coefficient
[math]F_t \qquad [/math] flushing time
[math]H \qquad [/math] total water depth [math]D+\zeta[/math]
[math]K \qquad [/math] eddy diffusivity
[math]J \qquad [/math] buoyancy input
[math]k \qquad [/math] wave number ([math]2 \pi / \lambda[/math])
[math]L \qquad [/math] estuary length
[math]L_I \qquad [/math] salinity intrusion length
[math]M2 \qquad [/math] principal lunar semi-diurnal tidal constituent
[math]P \qquad [/math] tidal period
[math]Q \qquad [/math] river flow
[math]S_L \qquad [/math] axial bed slope
[math]S2 \qquad [/math] principal solar semi-diurnal tidal constituent
[math]t_{50} \qquad [/math] half-life in suspension
[math]U \qquad [/math] tidal current amplitude
[math]U_0 \qquad [/math] velocity component of river flow
[math]V \qquad [/math] volume
[math]W_s \qquad [/math] sediment fall velocity
[math]Z \qquad [/math] tidal elevation amplitude
[math]a \qquad [/math] exponential decay rate of suspended sediments [math]exp (-aC) [/math]
[math]\tan \alpha \qquad [/math] side slope gradient ([math]B/2D[/math])
[math]\zeta \qquad [/math] tide level relative to msl
[math]\theta \qquad [/math] phase advance of [math]\zeta[/math] relative to U
[math]\lambda \qquad [/math] wavelength
[math]\rho \qquad [/math] density
[math]\omega \qquad [/math] tidal frequency ([math]P / 2\pi[/math])
Related articles
Definitions, processes and models in morphology
Estuarine morphological modelling
References
- PRANDLE, D., 2009. Estuaries: dynamics, mixing, sedimentation and morphology.235pp Cambridge University Press, Cambridge, UK. 236pp
- (UK) ENVIRONMENT AGENCY Report: SC08001 16/R1 101pp 1/03/2010
Vulnerability of estuaries to sea level rise- stage 1: a review D PRANDLE https:www.gov.uk/government/uploads/system/
- PRANDLE, D. & LANE, A. 2015.
Sensitivity of estuaries to sea level rise: Vulnerability Indices Estuarine, Coastal & Shelf Sciences. 160, 60-68
Please note that others may also have edited the contents of this article.
|