Difference between revisions of "Ocean and shelf tides"
Dronkers J (talk | contribs) (Created page with " ==Introduction== Tidal motion is the oscillation of ocean waters under influence of the attractive gravitational forces of the moon and the sun. The response of the ocean t...") |
Dronkers J (talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | |||
| + | '''In this article the term tide refers to the astronomical tide.''' | ||
| + | |||
==Introduction== | ==Introduction== | ||
| − | Tidal motion is the oscillation of ocean waters under influence of the attractive gravitational forces of the moon and the sun. The response of the ocean to the gravitational forces follows a pattern of rotating ('amphidromic') systems, as a consequence of | + | Tidal motion is the oscillation of ocean waters under influence of the attractive gravitational forces of the moon and the sun. The response of the ocean to the gravitational forces follows a pattern of rotating ('amphidromic') systems, as a consequence of earth's rotation. The frequencies are determined by the relative periodic motions of moon, sun and earth surface. The amplitude of the tidal oscillation is very small compared to ocean depths. The tidal oscillation in each point can therefore be represented by a linear superposition of sinusoidal tidal components. The most important tidal components have a periodicity which is close to semidiurnal or diurnal, due to earth's rotation. |
This article is an adaptation of the sections on ocean tides from the book Dynamics of Coastal Systems <ref name=D>Dronkers, J. 2016. Dynamics of Coastal Systems. World Scientific Publ. Co., Advanced Series on Ocean Engineering, 740 pp.</ref>. | This article is an adaptation of the sections on ocean tides from the book Dynamics of Coastal Systems <ref name=D>Dronkers, J. 2016. Dynamics of Coastal Systems. World Scientific Publ. Co., Advanced Series on Ocean Engineering, 740 pp.</ref>. | ||
| Line 10: | Line 13: | ||
===Moon and sun=== | ===Moon and sun=== | ||
| − | The regular daily upward and downward motion of the water surface along the coastline is the most visible expression of tidal forcing. In ancient Greece it was recognized that tides are in some way related to sun and moon, but this relationship could not be explained <ref>Ekman, M. 1993. A concise history of the theories of tides, precession-nutation and polar motion. Surveys in Geophysics 14: 585-617</ref>. The explanation of tidal motion as a consequence of gravitational forces was given by Newton. The lunar and solar tide generating forces acting on the oceans are extremely small; they are a factor <math>\, | + | The regular daily upward and downward motion of the water surface along the coastline is the most visible expression of tidal forcing. In ancient Greece it was recognized that tides are in some way related to sun and moon, but this relationship could not be explained <ref>Ekman, M. 1993. A concise history of the theories of tides, precession-nutation and polar motion. Surveys in Geophysics 14: 585-617</ref>. The explanation of tidal motion as a consequence of gravitational forces was given by Newton. The lunar and solar tide generating forces acting on the oceans are extremely small; they are about a factor <math>\, 10^{-7} \,</math> smaller than the gravitational force of the earth. The tide-generating force of the moon is about twice as large as that of the sun. |
| − | |||
===Tidal wave and ocean basin resonance=== | ===Tidal wave and ocean basin resonance=== | ||
| Line 18: | Line 20: | ||
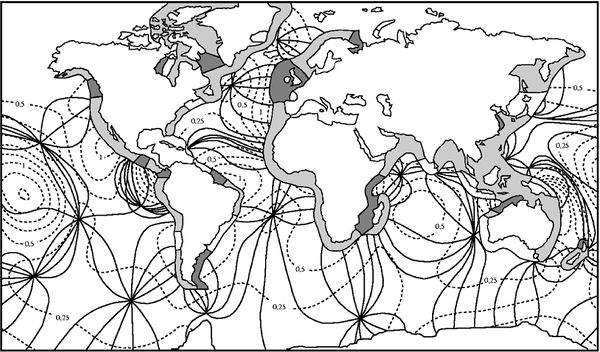
[[Image: worldtides.jpeg|thumb|center|600px|Fig.1. System of semidiurnal lunar tidal waves (M2) in the oceans represented by lines of equal tidal phase (solid, intervals of 30<math>^{\circ}</math>) and lines of equal tidal amplitude (dashed, intervals of 0.25 m). Three ranges are indicated for the tidal amplitude <math>a</math> on the continental shelf: microtidal (white fringe, <math>a < </math> 1 m), mesotidal (light grey fringe, 1 <math> < a < </math> 2 m) and macrotidal (dark grey fringe, <math>a > </math> 2 m). Redrawn after Bearman (1991) <ref> Bearman, G. (Ed.) 1991. Waves, tides and shallow-water processes. The Open University, Pergamon Press, Oxford</ref>]] | [[Image: worldtides.jpeg|thumb|center|600px|Fig.1. System of semidiurnal lunar tidal waves (M2) in the oceans represented by lines of equal tidal phase (solid, intervals of 30<math>^{\circ}</math>) and lines of equal tidal amplitude (dashed, intervals of 0.25 m). Three ranges are indicated for the tidal amplitude <math>a</math> on the continental shelf: microtidal (white fringe, <math>a < </math> 1 m), mesotidal (light grey fringe, 1 <math> < a < </math> 2 m) and macrotidal (dark grey fringe, <math>a > </math> 2 m). Redrawn after Bearman (1991) <ref> Bearman, G. (Ed.) 1991. Waves, tides and shallow-water processes. The Open University, Pergamon Press, Oxford</ref>]] | ||
| + | |||
| + | ===Modelling ocean tides=== | ||
| + | Modelling ocean tides remains a challenge, even with modern fast computers. Because the tidal wavelength is much larger than the ocean depth, these models are generally based on the hydrostatic shallow-water equations. Relatively simple models considering the response of a homogeneous ocean to the tide-generating forces yield results in qualitative agreement with observations. However, for better quantitative agreement stratification and internal tide generation (at ocean ridges, in particular) should be included. Other factors that need to be taken into account are: | ||
| + | *Seafloor deformation under the weight of the water column; | ||
| + | *Seafloor deformation related to the solid earth tide; | ||
| + | *Gravitational attraction induced by the mass of the ocean on the ocean itself. | ||
| + | See Hendershott (2007) <ref> Hendershott, M.C. 2007. Long Waves and Ocean Tides. In: Evolution of Physical Oceanography (Eds. B. Warren, and C. Wunsch) MIT OpenCourseWare, https://ocw.mit.edu </ref> for a discussion of these different factors. | ||
| Line 41: | Line 50: | ||
There are many other tidal components of smaller magnitude and lower frequency related to periodicity in the lunar and terrestrial orbits. A modulation of the mean tidal amplitude of the order of 5% is related to the 18.6 year oscillation in the declination of the lunar orbit. | There are many other tidal components of smaller magnitude and lower frequency related to periodicity in the lunar and terrestrial orbits. A modulation of the mean tidal amplitude of the order of 5% is related to the 18.6 year oscillation in the declination of the lunar orbit. | ||
| + | |||
| + | ===Prediction of tides=== | ||
| + | Because the astronomical tide responds to a cyclic forcing by the gravitational motions of earth, moon and sun (including earth's rotation), tides are a cyclic phenomenon at any place on earth and can be predicted by analysing observations from the past. Therefore the amplitude and phase of all relevant tidal components need to be determined. The most usual method today is based on the least-squares technique <ref> Parker, B.B. 2007. Tidal Analysis and Prediction. NOAA Special Publication NOS CO-OPS 3</ref>. The tidal elevation is represented by a sum of the (sinusoidal) tidal components that are expected to yield a significant contribution. The amplitudes and phases of the tidal components are free parameters which are determined by a least-square fit of the representation to the observed tidal elevation record. The tidal record should be sufficiently long to eliminate meteorological influences. The observation record should also be longer (at least a few times) than the largest period appearing in the representation. For resolving two components with close periods <math>T</math> and <math>T+\Delta T</math> the length of the observation record should exceed a few times <math>\; T^2 / \Delta T </math>. For many stations around the world tidal predictions are available (see for example https://maree.shom.fr/) . | ||
===Asymmetric ocean tides=== | ===Asymmetric ocean tides=== | ||
| Line 53: | Line 65: | ||
===Tidal amplification=== | ===Tidal amplification=== | ||
| − | The tides generated in the ocean propagate to the continental shelf, where the tidal range may increase further. Different phenomena contribute to this amplification: resonant dimensions of the shelf sea, slowing down of wave-energy propagation ('shoaling') or concentration of the tidal energy flux in areas of reduced width ('funneling'). The maximum spring tidal range can exceed 14 m in some funnel-shaped bays, such as | + | The tides generated in the ocean propagate to the continental shelf, where the tidal range may increase further. Different phenomena contribute to this amplification: resonant dimensions of the shelf sea, slowing down of wave-energy propagation ('shoaling') or concentration of the tidal energy flux in areas of reduced width ('funneling'). The maximum spring tidal range can exceed 14 m in some funnel-shaped bays, such as Bay of Fundy (Canada), Bristol Channel (UK) and Baie du Mont Saint Michel (France). |
Tidal amplification in shelf seas is counteracted by frictional momentum dissipation. The strong tidal motion occurring in many shelf seas is thus not locally produced by tide generating forces, but results from co-oscillation with ocean tides and from local topographic amplification. Numerical tidal studies for the northwest European shelf <ref> Pingree, R.D. and Griffiths, D.K. 1987. Tidal friction for semidiurnal tides. Cont.Shelf Res. 7: 1181-1209</ref> and for the East China shelf <ref> Kang, S.K., Lee, S.R. and Lie, H.J. 1998. Fine-grid tidal modelling of the Yellow and East China seas. Cont.Shelf Res. 18: 739-772</ref> show that the local tide generating force influences the co-oscillating semidiurnal tide in these shelf seas by no more than about 1%. This is the main reason why no substantial tidal motion is generated in shallow enclosed seas or lakes. Energy dissipation of ocean tidal energy is mainly due to frictional dissipation in shelf seas <ref>Munk, W. 1997. Once again: once again - tidal friction. Prog. Oceanog. 40: 7-35</ref>; however, non-negligible dissipation takes place also in the ocean <ref>Egbert, G.D. and Ray, R.D. 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405: 775-778</ref>. Tidal resonance in shelf seas generally has a damping effect on ocean tides <ref> Arbic, B.K., Karsten, R.H. and Garrett, C. 2009. On tidal resonance in the global ocean and the back‐effect of coastal tides upon open‐ocean tides. Atmosphere-Ocean, 47: 239-266</ref>. | Tidal amplification in shelf seas is counteracted by frictional momentum dissipation. The strong tidal motion occurring in many shelf seas is thus not locally produced by tide generating forces, but results from co-oscillation with ocean tides and from local topographic amplification. Numerical tidal studies for the northwest European shelf <ref> Pingree, R.D. and Griffiths, D.K. 1987. Tidal friction for semidiurnal tides. Cont.Shelf Res. 7: 1181-1209</ref> and for the East China shelf <ref> Kang, S.K., Lee, S.R. and Lie, H.J. 1998. Fine-grid tidal modelling of the Yellow and East China seas. Cont.Shelf Res. 18: 739-772</ref> show that the local tide generating force influences the co-oscillating semidiurnal tide in these shelf seas by no more than about 1%. This is the main reason why no substantial tidal motion is generated in shallow enclosed seas or lakes. Energy dissipation of ocean tidal energy is mainly due to frictional dissipation in shelf seas <ref>Munk, W. 1997. Once again: once again - tidal friction. Prog. Oceanog. 40: 7-35</ref>; however, non-negligible dissipation takes place also in the ocean <ref>Egbert, G.D. and Ray, R.D. 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405: 775-778</ref>. Tidal resonance in shelf seas generally has a damping effect on ocean tides <ref> Arbic, B.K., Karsten, R.H. and Garrett, C. 2009. On tidal resonance in the global ocean and the back‐effect of coastal tides upon open‐ocean tides. Atmosphere-Ocean, 47: 239-266</ref>. | ||
| Line 61: | Line 73: | ||
[[Image:worldmapM4.png|thumb|right|400px|Fig.3. Coastal zones with important quarter-diurnal tide.]] | [[Image:worldmapM4.png|thumb|right|400px|Fig.3. Coastal zones with important quarter-diurnal tide.]] | ||
| − | Tides on the continental shelf are due to co-oscillation with the ocean tides at the continental shelf boundaries, as noted earlier. However, the non-linearity of tidal propagation in shallow environments with strong topography | + | Tides on the continental shelf are due to co-oscillation with the ocean tides at the continental shelf boundaries, as noted earlier. However, the non-linearity of tidal propagation in shallow environments with strong topography (presence of large tidal flats, for example) alters the sinusoidal character of the ocean tide at the shelf boundary. The distortion of the tidal wave can be represented by additional tidal components corresponding to multiples of the dominant ocean tidal frequencies <ref> Aubrey, D.G. and Speer, P.E. 1985. A study of non-linear tidal propagation in shallow inlet/estuarine systems. Part I: Observations. Est. Coast. Shelf Sci. 21: 185-205</ref><ref> Friedrichs, C. T., and Aubrey, D. G. 1988. Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis. Estuarine, Coastal and Shelf Science, 27: 521-545</ref><ref>Boy, J.-P., Llubes, M., Ray, R., Hinderer, J., Florsch, N., Rosat, S., Lyard, F. and Letellier, T. 2004. Non-linear oceanic tides observed by superconducting gravimeters in Europe. J. Geodynamics 38: 391–405</ref>. An important consequence of tidal wave distortion is the asymmetric character of tidal motion in shallow water: the periods of tidal rise and tidal fall are not equal. This asymmetry is represented in particular by a quarter-diurnal tidal component (indicated by M4). Flood currents and ebb currents have different strength, as explained below. In Fig. 3 coastal regions are indicated with an important M4 tidal component; they coincide largely with coastal zones where the semidiurnal tide is strong (Fig. 2). Tidal asymmetry in shallow coastal waters, estuaries and tidal rivers, plays a crucial role in tide-topography interaction <ref name=D></ref>, because of the highly non-linear dependence of sediment transport on tidal current strength. |
| + | |||
| + | ===Ebb-flood asymmetry=== | ||
| + | |||
| + | [[Image:TidalBorePetitcodiacRiver.jpg|thumb|right|400px|Fig.4. Tidal bore in the Petitcodiac River (Bay of Fundy, Canada).]] | ||
| + | |||
| + | In bays and estuaries where the tidal amplitude is comparable to or larger than the average water depth the high-water crest of the tidal wave travels much faster than the low-water trough. In this case the tidal wave distortion can become so strong that the high-water crest overtakes the low-water trough. The tidal flood wave then propagates inland as a bore. Tidal bores are common in funnel-shaped shallow bays and estuaries with strongly amplified tides (for example the funnel-shaped bays mentioned above), especially for spring tidal conditions <ref>Bonneton, P., Bonneton, N., Parisot, J.-P. and Castelle B. 2015. Tidal bore dynamics in funnel-shaped estuaries, J. Geophys. Res. Oceans 120: 923–941, doi:10.1002/2014JC010267.</ref>. The flood current during the passage of the bore is very strong and largely exceeds the maximum currents occurring during ebb. The most famous tidal bore occurs in the Qiantang estuary (China) <ref>Jiyu, C., Cangzi, L., Chongle, Z. and Walker, H.J. 1990. Geomorphological development and sedimentation in Qiantang estuary and Hangzou Bay. J.Coast.Res. 6: 559-572</ref>. | ||
| + | |||
| + | More in general, one may distinguish two causes of tidal wave asymmetry <ref> Dronkers, J. 1986. Tidal asymmetry and estuarine morphology. Neth.J.Sea Res. 20: 117-131</ref>. | ||
| + | |||
| + | # Water depths at high water are substantially smaller than at low water and frictional dissipation is much stronger during the passage of the high-water crest than during the passage of the low-water trough. The tidal wave crest then propagates faster than the tidal wave trough and the period of tidal rise will thus be shorter than the period of tidal fall. This implies that flood currents will be on average stronger than ebb currents. | ||
| + | #The main tidal channel is bordered by large intertidal flats. The propagation of the tidal wave crest is retarded, because of lateral expansion of the tidal flood wave over the intertidal flats. The high-water wave crest then propagates more slowly than the low-water wave trough, which travels through the main tidal channel. In this case the period of tidal rise will be longer than the period of tidal fall and consequently ebb currents will be on average stronger than flood currents. | ||
| + | |||
| + | In most shallow tidal bays and estuaries both processes compete. This competition may lead to approximately equal strength of flood and ebb currents, in spite of strong nonlinearity of tidal wave propagation in these systems. When flood and ebb currents have approximately equal strength the tidally averaged residual sediment transport along the system will be small and the tidal system bathymetry will be in a state close to morphodynamic equilibrium <ref>Dronkers, J. 1998. Morphodynamics of the Dutch Delta. In: Physics of estuaries and coastal seas. Ed.: J.Dronkers and M.B.A.M. Scheffers, Balkema, Rotterdam: 297-304</ref>, see the article [[Morphology of estuaries]]. | ||
| + | |||
| + | |||
| + | ==Related articles== | ||
| + | |||
| + | [[Tidal motion in shelf seas]] | ||
| + | |||
| + | [[Coriolis acceleration]] | ||
| + | |||
| Line 68: | Line 101: | ||
Cartwright, D.E. 1999. Tides, a scientific history. Cambridge Univ.Press, UK, 292 pp. | Cartwright, D.E. 1999. Tides, a scientific history. Cambridge Univ.Press, UK, 292 pp. | ||
| − | + | Pedlosky, J. 1979. Geophysical Fluid Dynamics. Springer Verlag, 624 pp. | |
| − | |||
Revision as of 15:17, 29 September 2018
In this article the term tide refers to the astronomical tide.
Contents
Introduction
Tidal motion is the oscillation of ocean waters under influence of the attractive gravitational forces of the moon and the sun. The response of the ocean to the gravitational forces follows a pattern of rotating ('amphidromic') systems, as a consequence of earth's rotation. The frequencies are determined by the relative periodic motions of moon, sun and earth surface. The amplitude of the tidal oscillation is very small compared to ocean depths. The tidal oscillation in each point can therefore be represented by a linear superposition of sinusoidal tidal components. The most important tidal components have a periodicity which is close to semidiurnal or diurnal, due to earth's rotation.
This article is an adaptation of the sections on ocean tides from the book Dynamics of Coastal Systems [1].
Tide generation
Moon and sun
The regular daily upward and downward motion of the water surface along the coastline is the most visible expression of tidal forcing. In ancient Greece it was recognized that tides are in some way related to sun and moon, but this relationship could not be explained [2]. The explanation of tidal motion as a consequence of gravitational forces was given by Newton. The lunar and solar tide generating forces acting on the oceans are extremely small; they are about a factor [math]\, 10^{-7} \,[/math] smaller than the gravitational force of the earth. The tide-generating force of the moon is about twice as large as that of the sun.
Tidal wave and ocean basin resonance
Ocean tides owe their strength for a large part to resonance; tidal motion is amplified for tidal components with a frequency close to the frequency of free oscillations in the ocean basins. This is the case in particular for the semi-diurnal tide in the North Atlantic and Pacific Oceans [3], and also for the diurnal tide in the Pacific ocean [4]. Tidal waves in wide ocean basins (width typically larger than a few thousand km) rotate around points of zero amplitude, the amphidromic points; the rotation is counterclockwise in the Northern Hemisphere and clockwise in the Southern Hemisphere. This due to earth's rotation, which induces Coriolis acceleration of tidal currents. Fig.1 shows the semi-diurnal tidal wave in the world's oceans; it comprises a large number of amphidromic systems, where the tide rotates in resonance with the semi-diurnal component of the gravitational force. This ocean tidal wave pattern can be described in first approximation by a combination of Kelvin and Sverdrup waves (also called Poincaré waves, see Tidal motion in shelf seas).
Modelling ocean tides
Modelling ocean tides remains a challenge, even with modern fast computers. Because the tidal wavelength is much larger than the ocean depth, these models are generally based on the hydrostatic shallow-water equations. Relatively simple models considering the response of a homogeneous ocean to the tide-generating forces yield results in qualitative agreement with observations. However, for better quantitative agreement stratification and internal tide generation (at ocean ridges, in particular) should be included. Other factors that need to be taken into account are:
- Seafloor deformation under the weight of the water column;
- Seafloor deformation related to the solid earth tide;
- Gravitational attraction induced by the mass of the ocean on the ocean itself.
See Hendershott (2007) [6] for a discussion of these different factors.
Tidal components
Semidiurnal periodicity
In order to explain tidal motion, it is not sufficient to consider only the gravitational forces exerted by moon and sun on the earth's water masses. Tide generation results from the local imbalance at the earth's surface of two opposing factors: the gravitational forces acting between the earth and the moon (and between the earth and the sun), and the outward centrifugal acceleration related to the orbital motions of these celestial bodies. In fact, only the tangential component of the resulting force is relevant, which points towards the equator. Because the gravitational force and the centrifugal force cancel at any location on the earth's surface twice during each diurnal rotation, the major periodicity is approximately semidiurnal (a little more than 12 hours because of moon's orbital motion).
Diurnal tide and spring-neap cycle
Because the solar and lunar orbits do not coincide with the equatorial plane (the angle between orbital plane and equatorial plane is called declination), a daily inequality arises in the semidiurnal cycle. The daily inequality is strongest in shelf seas that resonate at diurnal frequency and which are situated close to amphodromic points of the semidiurnal tide. In such regions the tide is mainly diurnal.
Due to the [math]\approx[/math] 30-day orbital motion of the moon, the moon-earth and sun-earth axes approximately coincide every 15 days (syzygy). This causes a 15-day cycle of neap tide and spring tide; spring tide follows full moon and new moon and neap tide follows half-moon (with a delay of one or two days due to frictional dissipation [7]). In fact, the 15-day period corresponds to the frequency difference of the semidiurnal lunar component ([math]M_2[/math]) and the semidiurnal solar component ([math]S_2[/math]); the interference of these components produces the neap-spring variation of the tidal amplitude.
Other tidal components
The different cycles in the relative motions of moon, sun and earth surface generate tidal waves with corresponding periods. The lunar semidiurnal tidal component ([math]M_2[/math], period [math]\approx[/math] 12 h 25 min) is generally the largest tidal constituent (see Fig.2), followed by the semidiurnal solar tide [math]S_2[/math]. Other important tidal constituents are:
- the diurnal component [math]K_1[/math], which is related to the declination of the lunar and solar orbits relative to the equatorial plane (period [math]\approx[/math] 24 h),
- the diurnal lunar component [math]O_1[/math] (period [math]\approx[/math] 26 h) and
- the diurnal solar component [math]P_1[/math] (period [math]\approx[/math] 24 h).
There are many other tidal components of smaller magnitude and lower frequency related to periodicity in the lunar and terrestrial orbits. A modulation of the mean tidal amplitude of the order of 5% is related to the 18.6 year oscillation in the declination of the lunar orbit.
Prediction of tides
Because the astronomical tide responds to a cyclic forcing by the gravitational motions of earth, moon and sun (including earth's rotation), tides are a cyclic phenomenon at any place on earth and can be predicted by analysing observations from the past. Therefore the amplitude and phase of all relevant tidal components need to be determined. The most usual method today is based on the least-squares technique [8]. The tidal elevation is represented by a sum of the (sinusoidal) tidal components that are expected to yield a significant contribution. The amplitudes and phases of the tidal components are free parameters which are determined by a least-square fit of the representation to the observed tidal elevation record. The tidal record should be sufficiently long to eliminate meteorological influences. The observation record should also be longer (at least a few times) than the largest period appearing in the representation. For resolving two components with close periods [math]T[/math] and [math]T+\Delta T[/math] the length of the observation record should exceed a few times [math]\; T^2 / \Delta T [/math]. For many stations around the world tidal predictions are available (see for example https://maree.shom.fr/) .
Asymmetric ocean tides
Because of the minor role of friction in the propagation of ocean tides, individual astronomic tidal components are well described by sinusoidal functions. This implies that for each component the rising and falling branches are symmetric. This also holds on average for a superposition of tidal components, if the frequencies [math]\omega_i[/math] of the major tidal components are not linearly related with integer coefficients ([math]\omega_i[/math] is different from any combination of sums and differences of [math]\omega_j, \; j \neq i[/math]). Taken over a sufficiently long time interval the average period of rising tide equals the average period of falling tide. Hence, at the continental shelf boundary there is symmetry between the astronomical forcing of flood currents and ebb currents.
However, certain combinations of astronomic components yield asymmetric tides, irrespective of the averaging period. The reason is that most tidal constituents result from a superposition of a limited number of basic cycles in the relative motions of earth, moon and sun. The frequencies of these tidal constituents correspond to sums and differences of the basic frequencies [9]. This implies that different tidal constituents may interfere in such a way that flood and ebb are modulated in a systematic, asymmetric way. Such asymmetries may become significant in the case of strong diurnal tides; for dominant semidiurnal tides this effect is small [10].
A particular example is the combination of the [math]M_2, K_1[/math] and [math]O_1[/math] tides. The sum of the frequencies of the [math]K_1[/math] and [math]O_1[/math] tidal constituents equals the frequency of the [math]M_2[/math] tidal constituent. In regions where the amplitudes of the [math]K_1[/math] and [math]O_1[/math] tides are not small compared to the amplitude of the [math]M_2[/math] tide, the sum of these three tidal constituents yields an asymmetric tide, with an asymmetry depending on the respective phases of these tidal constituents. In this case the astronomic forcing of flood and ebb currents at the continental shelf boundary is nor symmetric, with consequences for residual sediment transport.
Tides on the continental shelf
Tidal amplification
The tides generated in the ocean propagate to the continental shelf, where the tidal range may increase further. Different phenomena contribute to this amplification: resonant dimensions of the shelf sea, slowing down of wave-energy propagation ('shoaling') or concentration of the tidal energy flux in areas of reduced width ('funneling'). The maximum spring tidal range can exceed 14 m in some funnel-shaped bays, such as Bay of Fundy (Canada), Bristol Channel (UK) and Baie du Mont Saint Michel (France).
Tidal amplification in shelf seas is counteracted by frictional momentum dissipation. The strong tidal motion occurring in many shelf seas is thus not locally produced by tide generating forces, but results from co-oscillation with ocean tides and from local topographic amplification. Numerical tidal studies for the northwest European shelf [11] and for the East China shelf [12] show that the local tide generating force influences the co-oscillating semidiurnal tide in these shelf seas by no more than about 1%. This is the main reason why no substantial tidal motion is generated in shallow enclosed seas or lakes. Energy dissipation of ocean tidal energy is mainly due to frictional dissipation in shelf seas [13]; however, non-negligible dissipation takes place also in the ocean [14]. Tidal resonance in shelf seas generally has a damping effect on ocean tides [15].
Higher harmonic components
Tides on the continental shelf are due to co-oscillation with the ocean tides at the continental shelf boundaries, as noted earlier. However, the non-linearity of tidal propagation in shallow environments with strong topography (presence of large tidal flats, for example) alters the sinusoidal character of the ocean tide at the shelf boundary. The distortion of the tidal wave can be represented by additional tidal components corresponding to multiples of the dominant ocean tidal frequencies [16][17][18]. An important consequence of tidal wave distortion is the asymmetric character of tidal motion in shallow water: the periods of tidal rise and tidal fall are not equal. This asymmetry is represented in particular by a quarter-diurnal tidal component (indicated by M4). Flood currents and ebb currents have different strength, as explained below. In Fig. 3 coastal regions are indicated with an important M4 tidal component; they coincide largely with coastal zones where the semidiurnal tide is strong (Fig. 2). Tidal asymmetry in shallow coastal waters, estuaries and tidal rivers, plays a crucial role in tide-topography interaction [1], because of the highly non-linear dependence of sediment transport on tidal current strength.
Ebb-flood asymmetry
In bays and estuaries where the tidal amplitude is comparable to or larger than the average water depth the high-water crest of the tidal wave travels much faster than the low-water trough. In this case the tidal wave distortion can become so strong that the high-water crest overtakes the low-water trough. The tidal flood wave then propagates inland as a bore. Tidal bores are common in funnel-shaped shallow bays and estuaries with strongly amplified tides (for example the funnel-shaped bays mentioned above), especially for spring tidal conditions [19]. The flood current during the passage of the bore is very strong and largely exceeds the maximum currents occurring during ebb. The most famous tidal bore occurs in the Qiantang estuary (China) [20].
More in general, one may distinguish two causes of tidal wave asymmetry [21].
- Water depths at high water are substantially smaller than at low water and frictional dissipation is much stronger during the passage of the high-water crest than during the passage of the low-water trough. The tidal wave crest then propagates faster than the tidal wave trough and the period of tidal rise will thus be shorter than the period of tidal fall. This implies that flood currents will be on average stronger than ebb currents.
- The main tidal channel is bordered by large intertidal flats. The propagation of the tidal wave crest is retarded, because of lateral expansion of the tidal flood wave over the intertidal flats. The high-water wave crest then propagates more slowly than the low-water wave trough, which travels through the main tidal channel. In this case the period of tidal rise will be longer than the period of tidal fall and consequently ebb currents will be on average stronger than flood currents.
In most shallow tidal bays and estuaries both processes compete. This competition may lead to approximately equal strength of flood and ebb currents, in spite of strong nonlinearity of tidal wave propagation in these systems. When flood and ebb currents have approximately equal strength the tidally averaged residual sediment transport along the system will be small and the tidal system bathymetry will be in a state close to morphodynamic equilibrium [22], see the article Morphology of estuaries.
Related articles
Further reading
Cartwright, D.E. 1999. Tides, a scientific history. Cambridge Univ.Press, UK, 292 pp.
Pedlosky, J. 1979. Geophysical Fluid Dynamics. Springer Verlag, 624 pp.
References
- ↑ 1.0 1.1 Dronkers, J. 2016. Dynamics of Coastal Systems. World Scientific Publ. Co., Advanced Series on Ocean Engineering, 740 pp.
- ↑ Ekman, M. 1993. A concise history of the theories of tides, precession-nutation and polar motion. Surveys in Geophysics 14: 585-617
- ↑ Heath, R.A. 1981. Estimates of the resonant period and Q in the semi-diurnal tidal band in the North Atlantic and Pacific Oceans. Deep-Sea Research. Vol. 28A: 481 – 493
- ↑ Müller, M. 2007. The free oscillations of the world ocean in the period range 8 to 165 hours including the full loading effect. Geophys. Res. Letters 34, L05606, doi:10.1029/2006GL028870, 2007
- ↑ Bearman, G. (Ed.) 1991. Waves, tides and shallow-water processes. The Open University, Pergamon Press, Oxford
- ↑ Hendershott, M.C. 2007. Long Waves and Ocean Tides. In: Evolution of Physical Oceanography (Eds. B. Warren, and C. Wunsch) MIT OpenCourseWare, https://ocw.mit.edu
- ↑ Garrett, C.J.R. and Munk, W.H. 1971. The age of the tide and the "Q" of the oceans. Deep-Sea Res. 18: 493-503
- ↑ Parker, B.B. 2007. Tidal Analysis and Prediction. NOAA Special Publication NOS CO-OPS 3
- ↑ Doodson, A.T. 1921. The harmonic development of the tide-generating potential. Proc. R. Soc. London, Ser.A 100: 305-329
- ↑ Hoitink, A.F.J., Hoekstra, P. and van Mare, D.S. 2003. Flow asymmetry associated with astronomical tides: Implications for residual transport of sediment. J.Geophys.Res. 108: 13-1 - 13-8
- ↑ Pingree, R.D. and Griffiths, D.K. 1987. Tidal friction for semidiurnal tides. Cont.Shelf Res. 7: 1181-1209
- ↑ Kang, S.K., Lee, S.R. and Lie, H.J. 1998. Fine-grid tidal modelling of the Yellow and East China seas. Cont.Shelf Res. 18: 739-772
- ↑ Munk, W. 1997. Once again: once again - tidal friction. Prog. Oceanog. 40: 7-35
- ↑ Egbert, G.D. and Ray, R.D. 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405: 775-778
- ↑ Arbic, B.K., Karsten, R.H. and Garrett, C. 2009. On tidal resonance in the global ocean and the back‐effect of coastal tides upon open‐ocean tides. Atmosphere-Ocean, 47: 239-266
- ↑ Aubrey, D.G. and Speer, P.E. 1985. A study of non-linear tidal propagation in shallow inlet/estuarine systems. Part I: Observations. Est. Coast. Shelf Sci. 21: 185-205
- ↑ Friedrichs, C. T., and Aubrey, D. G. 1988. Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis. Estuarine, Coastal and Shelf Science, 27: 521-545
- ↑ Boy, J.-P., Llubes, M., Ray, R., Hinderer, J., Florsch, N., Rosat, S., Lyard, F. and Letellier, T. 2004. Non-linear oceanic tides observed by superconducting gravimeters in Europe. J. Geodynamics 38: 391–405
- ↑ Bonneton, P., Bonneton, N., Parisot, J.-P. and Castelle B. 2015. Tidal bore dynamics in funnel-shaped estuaries, J. Geophys. Res. Oceans 120: 923–941, doi:10.1002/2014JC010267.
- ↑ Jiyu, C., Cangzi, L., Chongle, Z. and Walker, H.J. 1990. Geomorphological development and sedimentation in Qiantang estuary and Hangzou Bay. J.Coast.Res. 6: 559-572
- ↑ Dronkers, J. 1986. Tidal asymmetry and estuarine morphology. Neth.J.Sea Res. 20: 117-131
- ↑ Dronkers, J. 1998. Morphodynamics of the Dutch Delta. In: Physics of estuaries and coastal seas. Ed.: J.Dronkers and M.B.A.M. Scheffers, Balkema, Rotterdam: 297-304
Please note that others may also have edited the contents of this article.
|