Difference between revisions of "Collapsible-Bag depth-integrating sampler"
Leovanrijn (talk | contribs) |
Leovanrijn (talk | contribs) |
||
| Line 26: | Line 26: | ||
[[Image:H5627figure1.jpg|thumb|left|Fig. 1: Transit rate curve]] | [[Image:H5627figure1.jpg|thumb|left|Fig. 1: Transit rate curve]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Revision as of 10:33, 3 June 2007
Contents
Collapsible-Bag sampler
The Collapsible-Bag sampler is based on the principle that the static pressure acting on the outside surface of the flexible bag (devoid of air) creates at the nozzle exit a pressure equal to the hydrostatic pressure at the nozzle entrance. Using this method, samples can be collected throughout any depth.
The sampler consists of a wide-mouth, perforated, rigid plastic container enclosed in a cage-like metal frame. The head of the frame supports a plastic intake nozzle (6 or 13 um) and swings open to permit the plastic container to be removed. When the head is closed, the end of the nozzle extends slightly into the mouth of the container. Perforations in the container allows the air in the container to escape during submergence. For sampling, a collapsed flexible plastic bag is placed inside the rigid container. The neck of the flexible bag is stretched over the neck of the rigid container and this unit is placed into the sampler.
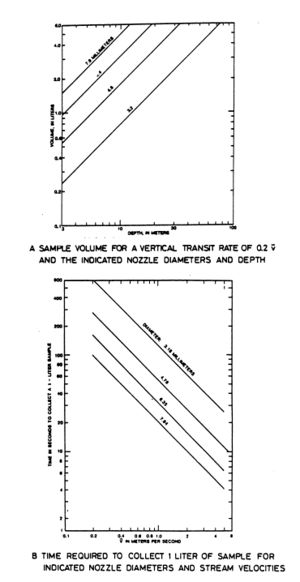
When the sampler is lowered into the flow, water enters the perforations in the rigid container, surrounds the collapsed bag and equalizes the hydrostatic pressure at the nozzle entrance. The velocity head forces water through the intake nozzle into the collapsed bag, which unfolds to conform to the rigid container. This sampling action eliminates any possibility for flow to rush in due to unequal pressures and insures that water-sediment mixture is collected at stream velocity regardless of velocity distribution and depth, provided that the sample container does not overfill and the vertical transit rate is smaller than 0.4 of the depth-averaged velocity. Nordin et al., 1983 have used a large-volume (6 litres) bag sampler in combination with an Ott-type current meter in water depths up to 30 m. The rotation of the propeller was transmitted into a rate meter. This latter provided a direct read out of velocity. By lowering and raising the current meter over the depth, the instantaneous velocity profile can be recorded. The constant vertical transit rate of the bag sampler should be fast enough so that the sample container is not completely filled, but not greater than 0.4 v (v= depth-averaged velocity). Nordin et al., 1983 tried to keep the transit rate smaller than 0.2 v .
The sample volumes that will be collected for a transit rate equal to 0.2 v are given in Figure 1 A. The mean velocity v can be estimated from the surface velocity. The time required to collect one liter of sample for various mean velocities and nozzle diameters is given in Figure 1B.
If the cross-channel distribution of sediment discharge is needed, each sample is processed separately. If the depth and velocity are fairly uniform across the section, it often is possible to use one nozzle diameter and transit rate at all verticals and the individual samples can be composited into a single discharge-weighted sample. For most purposes 10 to 15 depth-integrated samples equally spaced across the section are adequate. If the maximum and minimum surface velocities are observed when the cross-section is sounded initially, that information can be used with the data plotted in Figure 1B to select the transit rate. Usually, it is accurate enough to select a transit rate smaller than 0.2 v using the velocity v of the deepest en fastest vertical. Assuming that v does not vary more than a factor 2, the transit rate will not be greater than 0.4 v in the vertical with the lowest velocity.
The depth-averaged concentration can be determined as
c=G/V
in which: G= dry mass of sediment (mg), V= volume of water sample (l).
The depth-integrated suspended sediment transport (in kg/m/s) can be determined as:
S= G h/(F T) or as S=c u h= (G/V) u h
in which: G= dry mass of sediment (mg), V= volume of sediment sample, including pores (m3),h= depth of sampled zone (m), u= depth-averaged velocity (m/s), F= area of nozzle (m2), T= sampling period (s).
Photographs and Figures
References
Christiansen, H., 1985. Suspended Sediment Measurements in Elbe Estuary at Hamburg using a Cux Sampler. Euromech 192, Neubiberg, Germany.
Nordin, C.F., Cranston, C.C., Abel, M.B., 1983. New Technology for Measuring Water and Suspended Sediment Discharge of Large Rivers.
Stevens, H.H., Lutz, G.A. and Hubbel, D.W., 1980. Collapsible-Bag Suspended Sediment Sampler. Journal of Hydraulic Division, ASCE, Vol. 106, No. Hy4.
See also
Other contributions of Leo van Rijn
articles with parts of the manual
- INTRODUCTION, PROBLEMS AND APPROACHES IN SEDIMENT TRANSPORT MEASUREMENTS
- DEFINITIONS, PROCESSES AND MODELS IN MORPHOLOGY
- PRINCIPLES, STATISTICS AND ERRORS OF MEASURING SEDIMENT TRANSPORT
- COMPUTATION OF SEDIMENT TRANSPORT AND PRESENTATION OF RESULTS
- MEASURING INSTRUMENTS FOR SEDIMENT TRANSPORT
- MEASURING INSTRUMENTS FOR PARTICLE SIZE AND FALL VELOCITY
- MEASURING INSTRUMENTS FOR BED MATERIAL SAMPLING
- LABORATORY AND IN-SITU ANALYSIS OF SAMPLES
- IN-SITU MEASUREMENT OF WET BULK DENSITY
- INSTRUMENTS FOR BED LEVEL DETECTION
- ARGUS VIDEO
- MEASURING INSTRUMENTS FOR FLUID VELOCITY, PRESSURE AND WAVE HEIGHT
External links
Crediting the authors
Please note that others may also have edited the contents of this article.
|
[[Category:Articles by {{{AuthorFullName}}}]]
Please note that others may also have edited the contents of this article.
|
[[Category:Articles by {{{AuthorFullName}}}]]