Difference between revisions of "Sheet flow"
Dronkers J (talk | contribs) (Created page with " {{ Definition| title = Sheet flow | definition = Sheet-flow sediment transport refers to transport of sandy sediments as a fluidized thin surface layer (thickness of ten to a...") |
Dronkers J (talk | contribs) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
| + | Sheet flow is a particular form of bedload sediment transport in which the seabed is flattened and the top soil layer is fluidized. Sheet flow transport occurs when the seabed is subjected to high shear stresses, especially shear stresses generated by strong wave action. A fair approximation of this condition is given by the Shields parameter <math>\theta</math> , <ref>Wikramanayake, P.N. and Madsen, O.S. 1994. Calculation of Movable Bed Friction Factors. Technical Report. U.S. Army Engineer Waterways Experiment Station, Vicksburg, MS.</ref><ref>Kleinhans, M. G. 2005. Phase diagrams of bed states in steady, unsteady, oscillatory and mixed flows. In (editor L. van Rijn): Principles of Sedimentation and Erosion Engineering in Rivers, Estuaries and Coastal Seas, pp. Q1– Q16, Aqua, Blokzijl, Netherlands</ref> | ||
| + | <math>\theta \equiv \Large\frac{\tau_{b, max}}{\Delta \rho \, g \, d_{50}}\normalsize \, > \, \theta_s \approx 0.7 \, , </math> | ||
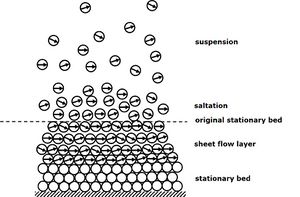
| + | where <math>\tau_{b,max} =</math> maximum total bed shear stress during the wave cycle, <math>\Delta \rho =</math> density difference between sediment and seawater, <math>d_{50} =</math> the median sediment grainsize and <math>g=</math> gravitational acceleration. This condition is usually satisfied for wave orbital velocities greater than 1 m/s. In the sheet-flow layer, continuous contacts between sand grains create an intergranular stress. This stress decreases the velocity in the sheet-flow layer to about one half the velocity in the top layer. The sediment concentration in the sheet-flow layer is in the order of 100 to 1000 kg/m<sup>3</sup>. | ||
| − | + | The formation of a sheet flow layer is promoted by cyclic wave loading of the seabed, see [[Wave-induced soil liquefaction]]. | |
| − | + | Flume experiments<ref>Mieras, R.S., Puleo, J.A., Anderson, D., Cox, D.T. and Hsu, T.-J. 2017. Large-scale experimental observations of sheet flow on a sandbar under skewed-asymmetric waves, J. Geophys. Res. Oceans 122: 5022–5045</ref> suggest that the maximum wave-generated sheet-flow layer thickness <math>\delta_{s, max}</math> depends linearly on the maximum bed shear stress <math>\tau_{b,max}</math>, | |
| + | <math>\delta_{s, max} = \Lambda \Large\frac{\tau_{b, max}}{g \Delta \rho} , </math> | ||
| + | where <math>\Lambda</math> a coefficient with values in the range 10-35. | ||
| + | ==Related articles== | ||
| + | :[[Sediment transport formulas for the coastal environment#Sheet-flow transport]]. | ||
| + | |||
| + | |||
| + | |||
| + | ==References== | ||
| + | <references/> | ||
Latest revision as of 15:22, 25 January 2025
Definition of Sheet flow:
Sheet-flow sediment transport refers to transport of sandy sediments as a fluidized thin surface layer (thickness of ten to a few tens of grains).
This is the common definition for Sheet flow, other definitions can be discussed in the article
|
Notes
Sheet flow is a particular form of bedload sediment transport in which the seabed is flattened and the top soil layer is fluidized. Sheet flow transport occurs when the seabed is subjected to high shear stresses, especially shear stresses generated by strong wave action. A fair approximation of this condition is given by the Shields parameter [math]\theta[/math] , [1][2]
[math]\theta \equiv \Large\frac{\tau_{b, max}}{\Delta \rho \, g \, d_{50}}\normalsize \, \gt \, \theta_s \approx 0.7 \, , [/math]
where [math]\tau_{b,max} =[/math] maximum total bed shear stress during the wave cycle, [math]\Delta \rho =[/math] density difference between sediment and seawater, [math]d_{50} =[/math] the median sediment grainsize and [math]g=[/math] gravitational acceleration. This condition is usually satisfied for wave orbital velocities greater than 1 m/s. In the sheet-flow layer, continuous contacts between sand grains create an intergranular stress. This stress decreases the velocity in the sheet-flow layer to about one half the velocity in the top layer. The sediment concentration in the sheet-flow layer is in the order of 100 to 1000 kg/m3.
The formation of a sheet flow layer is promoted by cyclic wave loading of the seabed, see Wave-induced soil liquefaction.
Flume experiments[3] suggest that the maximum wave-generated sheet-flow layer thickness [math]\delta_{s, max}[/math] depends linearly on the maximum bed shear stress [math]\tau_{b,max}[/math],
[math]\delta_{s, max} = \Lambda \Large\frac{\tau_{b, max}}{g \Delta \rho} , [/math]
where [math]\Lambda[/math] a coefficient with values in the range 10-35.
Related articles
References
- ↑ Wikramanayake, P.N. and Madsen, O.S. 1994. Calculation of Movable Bed Friction Factors. Technical Report. U.S. Army Engineer Waterways Experiment Station, Vicksburg, MS.
- ↑ Kleinhans, M. G. 2005. Phase diagrams of bed states in steady, unsteady, oscillatory and mixed flows. In (editor L. van Rijn): Principles of Sedimentation and Erosion Engineering in Rivers, Estuaries and Coastal Seas, pp. Q1– Q16, Aqua, Blokzijl, Netherlands
- ↑ Mieras, R.S., Puleo, J.A., Anderson, D., Cox, D.T. and Hsu, T.-J. 2017. Large-scale experimental observations of sheet flow on a sandbar under skewed-asymmetric waves, J. Geophys. Res. Oceans 122: 5022–5045
Please note that others may also have edited the contents of this article.
|