Wave-induced seabed liquefaction
Definition of Soil liquefaction:
When a water-saturated soil starts behaving as a fluid, losing stiffness and bearing capacity.
This is the common definition for Soil liquefaction, other definitions can be discussed in the article
|
Seabed soils which are not well consolidated are prone to liquefaction when exposed to pressure fluctuations. Soil liquefaction can be produced for example by earthquakes, but here we mainly concentrate on submarine soils which are exposed to cyclic loading by waves. Numerous incidents of collapsing or sinking structures built on freshly deposited subsea beds have been reported in the literature[1][2]. Soil liquefaction processes when structures are placed on or into the seabed were studied, inter alia, in the EU-funded Liquefaction Around Marine Structures (LIMAS) project[3]. These processes are more complicated due to wave-structure-soil interactions involving pressure fluctuations induced by structure motion.
A simplified mathematical introduction to the theory of soil liquefaction is given in the Appendix.
Contents
Two types of soil liquefaction
Two types of wave-induced soil liquefaction can be distinguished: Transient liquefaction (also called instantaneous or momentary liquefaction) and residual liquefaction. Both types can occur in poorly drained loosely packed soils, for example soils containing a high percentage of fine sandy or silty material. In well-drained soils, for example a coarse sandy or gravelly seabed, pore pressure by cyclic loading cannot build up, but transient liquefaction is possible.
Transient liquefaction
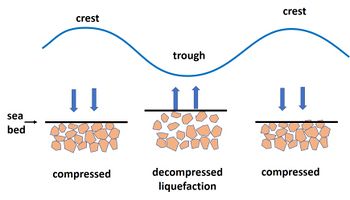
The upper layer of the seabed will liquefy if the pressure of the pore water deeper in the soil is higher than the submerged weight of the soil layer above. This can occur because the fluctuating water pressure exerted by surface waves is transmitted with vertically increasing delay and damping to the pore pressure in the seabed (as explained in the Appendix). In the period just before and after passage of the wave trough, the pressure deeper in the soil is higher than near the surface. The soil top layer then experiences an upward force, which can lift sediment particles near the seabed surface out of the soil skeleton, see Fig. 1. The soil top layer (typically ten to several tens of centimeters) becomes liquefied over a short period of time during which this condition prevails. One consequence is that objects deposited on the seabed can sink and become buried[5][1] or float up if the density of the object is less than that of the liquified soil. Transient liquefaction mainly occurs in sandy seabeds with relatively high permeability and compressive resistance.
Most observations of wave-induced transient liquefaction come from laboratory experiments. Proper scaling of wave propagation and soil consolidation requires centrifuge tests[6]. There are also some studies based on field observations, in the nearshore subtidal zone and in the intertidal zone. In the latter case it was found that even a small volume fraction of air in the soil can greatly dampen the transmission of wave-induced water pressure to the pore fluid[7].
Residual liquefaction
Soils prone to liquefaction are typically water-saturated, consisting of loosely packed fine sediments – fine sand, silt and some clay – with poor drainage capacity (low hydraulic conductivity). When such a soil is subjected to cyclic wave-induced loading and associated shear deformations, the soil grains tend to rearrange, mainly by sliding at the sediment particle contacts, such that the soil skeleton is progressively compressed. (In contrast, a densely compacted soil may expand.) If skeleton contraction is faster than pore water outflow, the resulting reduction of the pore volume leads to an increase of the pore water pressure. When the pore pressure exceeds the pressure exerted by the submerged weight of the overlying soil (i.e., the effective stress on the soil grains vanishes), the contact friction points between soil grains are broken and the soil skeleton collapses. The soil grains become unbound and free to move, carried by the pore water (Fig. 2). The soil begins to act like a liquid, losing its stiffness and bearing capacity. The liquified soil forms a two-layer system with the water above and in case of muddy soils, interfacial waves at the mudline, generated by the surface waves, may appear [8]. Any structures built on this soil will sink or collapse if its density is higher than the density of the liquified soil[1]. Sandy soils covered by a thin, poorly permeable topsoil that allows the penetration of dynamic wave pressure but impedes the drainage of pore water, are particularly susceptible to pore pressure build-up and residual liquefaction[9].
Experiments in a wave flume have shown that the residual pore pressure generated by random waves can be much higher than that by regular waves with equivalent mean wave height and period. Low-frequency waves in particular can make a significant contribution to the residual pressure[10]. Other flume experiments have shown that soil liquefaction through excess pore pressure enhances sediment re-suspension[11]. Seabed liquefaction and seabed scour can reinforce each other, as removal of top soil strengthens the upward pore pression gradient in the soil underneath[12].
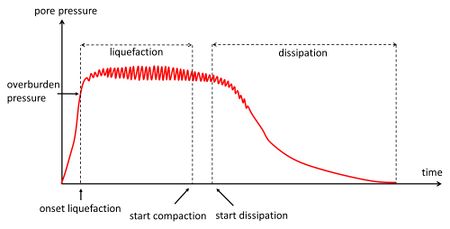
Liquefaction-consolidation process
The onset of residual liquefaction occurs first at the surface of the bed, and rapidly spreads out across the soil depth, causing the entire loose soil layer to behave like a liquid. When the liquefaction reaches the impermeable base, the soil begins to compact. The large pores between particles in the liquefied state allow the expel (drainage) of pore water. Pore water outflow and soil compaction are promoted by wave-induced pressure fluctuations (or by artificially generated soil vibrations)). Soil grains fall out of the liquid state, settle through the pore water until they come into contact with each other. The compaction gradually progresses from the impermeable base in the upward direction, and the entire sequence of the liquefaction/compaction process comes to an end when the compaction reaches the soil surface[13][14]. The compaction phase is associated with the formation of upward seepage channels and corresponding small sand boils or mud volcanoes on the seafloor[15]. After liquefaction, a loosely packed soil will not recover its initial state. The soil is compacted and much less susceptible to renewed liquefaction. The liquefaction-compaction process is depicted schematically in Fig. 3.
Influence of soil composition
Flume experiments show that the liquefaction potential strongly depends on the soil composition. Soil characteristics that strongly influence the susceptibility of soils to liquefaction are:
- Soil stiffness, commonly estimated by means of the shear modulus [math]G[/math], which is a measure of the soil's resistance to deformation. Soil stiffness depends in particular on the average contact area of the soil grains in the soil matrix.
- Poisson's ratio of soil, [math]\nu[/math], which is a measure of the ratio elongation/contraction of a soil sample subjected to vertical compression. Poisson's ratio is related to the internal friction angle [math]\phi[/math] of soil.
- The pore water compressibility [math]\beta[/math] (for submarine saturated soils). If the pores between the soil grains are completely filled with incompressible pore water, the wave-induced pressure on the soil is directly transferred to the soil skeleton. If the pore water contains a fraction [math]C[/math] of gas (air), the wave-induced pressure on the soil skeleton is partly absorbed by compaction of air bubbles.
- The soil porosity, [math]n[/math], the volume fraction not occupied by soil grains. Soil porosity is also expressed by means of the void ratio [math]e = n / (1-n) \;[/math] (volume of voids relative to the volume of solids).
- The soil’s permeability, commonly estimated by means of the hydraulic conductivity [math]K[/math]. The hydraulic conductivity indicates the extent to which soil water can escape from the soil matrix when exposed to wave-induced pressure. Soils susceptible to liquefaction typically have a poor drainage capacity.
These various parameters are not independent from each other. They all depend on the degree of soil compaction, which is commonly expressed by means of the soil’s relative density [math]D_r[/math],
[math]D_r = \dfrac{e_{max}-e}{e_{max}-e_{min}} \, , \quad e = \dfrac{n}{1-n}.[/math]
For a given soil composition, [math]e_{max} \, , e_{min}[/math] and [math]e[/math] are the maximum, minimum and actual void ratios.
The susceptibility of a soil to liquefaction can be assessed through Standard Penetration Tests or Cone Penetration Tests. More precise information on soil properties can be obtained from triaxial shear tests of soil samples. Triaxial shear tests of soil samples also enable the determination of soil characteristics needed to model soil behavior (see Appendix).
Experiments by Ishihara and Yamazaki (1984[17]) based on cyclic triaxial torsional shear tests show that the liquefaction susceptibility of fine saturated sand mainly depends on the relative soil density [math]D_r[/math] and the coefficient of neutral lateral earth pressure [math]K_0[/math]. The coefficient [math]K_0[/math] corresponds to the ratio of the lateral normal effective stress to the vertical effective stress for laterally homogeneous sand. For elastic deformations, [math]K_0 \approx 1 - \sin \phi \approx \nu / (1 - \nu)[/math], where the latter approximation only holds for elastic deformations. [18]
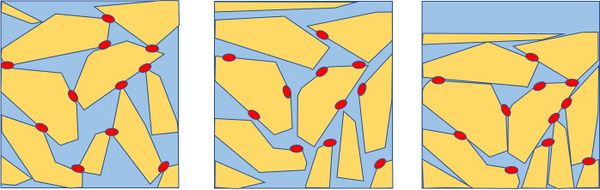
Experiments by Gratchev et al. (2006[19]) revealed the significant influence of plasticity on soil liquefaction resistance. Soil vulnerable to liquefaction had an open microfabric in which clay aggregates mainly gathered at the silt particle contact points, forming low-strength 'clay bridges' that were easily destroyed during cyclic loading (Fig. 2). The contact friction between particles that maintained the soil skeleton structure was reduced by the clay aggregates, so grains could easily slip and rotate once the seabed was subjected to wave loading. Clay minerals thus enhance the plasticity and compressibility of the clay-silt seabed and increases the sensitivity of the seabed to liquefaction.
Experiments with kaolinite-fine sand and illite-fine sand showed that the susceptibility of a soil to liquefaction increases with increasing clay content if the clay content is low (0.5-5%), but decreases with a higher clay content[20]. At a clay content of more than 10-30%, depending on the type of clay, the silt-clay mixture was not susceptible to liquefaction. This can be explained by the fact that in case of high clay content the silt grains are completely encapsulated in the clay matrix and therefore cannot rearrange under cyclic shear stresses, causing resistance to liquefaction. Experiments by Kirca et al. (2014[21]) showed that the sensitivity of a sand-clay mixture to wave-induced liquefaction not only depends on the clay content but also on the sand grainsize. Liquefaction occurred at a much larger clay content for medium sand than for fine sand or silt. The presence of shell fragments also decreases the susceptibility of silt to liquefaction[16]. Experiments for a medium-sand-clay (kaolinite) seabed supporting a submerged breakwater showed that wave-induced liquefaction required a clay content greater than 40%[22]. These experiment also showed that the initial water content in the soil is relevant to the liquefaction potential as it affects the pressure build-up process. Higher pore water fractions allow the residual pore pressure to accumulate faster.
The soil in an actual field situation usually has a long history of wave action, and hence it normally is a consolidated stiff soil, with low sensitivity to wave-induced liquefaction. This does not hold for freshly deposited soils. This may be the case, for example, where a pipeline is laid in a trench, and the trench is then backfilled[1].
Clay soils
The above description of soil liquefaction assumes that the soil initially consists of a granular skeleton that supports the weight of the overlying soil layers through stresses at the grain contact points. This assumption does not apply for clay soils, where clay minerals are mainly held together by electrochemical bounds. Consolidated clay soil can also be liquified by wave-induced pressure fluctuations, but the liquefaction process is different. Cohesive soil behaves like a viscoelastic material whose viscosity decreases when a (fluctuating) stress is applied that is strong enough to break the electrochemical bounds that hold the constituent particles together[23][24]. When the electrochemical bounds are broken, the released clay minerals form a colloidal suspension with the overlying water. The high stresses needed in case of advanced consolidation will more likely lead to sediment erosion and suspension rather than to liquefaction[25]. A fluid mud layer is formed when flocculent particles settle to the seabed in sufficiently high concentration. High concentrations of suspended fine sediment often originate from previous mud bed erosion by strong waves or currents or from convergence of residual fine sediment transport related to tidal asymmetry and estuarine circulation (see Estuarine turbidity maximum). Stirring of unconsolidated mud deposits by wave-induced pressure variations can also contribute to the formation of fluid mud[26]. When a fluid mud layer flows along the seabed, the density (and viscosity) can increase by bed erosion or decrease by uptake (entrainment) of overlying water[27]. Liquified clay soils reconsolidate after stress removal, eventually reaching a higher degree of compaction than before liquefaction[28]. However, consolidation of thick fluid mud layers is a very slow process. See also Fluid mud and Dynamics of mud transport.
Earthquake-induced liquefaction
Earthquakes also induce cyclic shear stresses in the seabed. They are caused by the upward propagation of longitudinal shear waves from the underlying rock formations. Shear stress fluctuations caused by earthquakes are of much shorter duration than wave-induced pressure fluctuations, but the frequency is much higher (typically a factor of 10). The resulting soil compaction is counteracted by an increase in pore pressure, because the short duration and high frequency of pressure fluctuations does not allow significant outflow of pore water. The effective confining stresses due to the weight of the overlying soil may therefore vanish when the state of sand packing is loose enough and the magnitude of cyclic shear stress is great enough, leading to a liquified soil state. Saturated soils consisting of loose sediments are therefore highly susceptible to liquefaction by earthquakes. [29][30].
Submarine slides on the shelf edge are among the major hazards caused by earthquake-induced seabed soil liquefaction. The shelf edge and slope area often contain recently deposited and under-consolidated materials. Due to the sloping stratigraphy, submarine slides can transport enormous sediment volumes during one single event on very gentle slopes with inclinations in the range 0.5 to 3°, over distances exceeding hundreds of kilometres.[31].
Preventing soil liquefaction
The risk of liquefaction can be reduced by replacing the existing soil layer with suitable materials, but this is usually an expensive solution. Soil consolidation can also be done by vibro compaction or by preloading the soft bed with coarse sediment[32]. Other methods for in situ soil consolidation are cement grouting or microbial-induced carbonate precipitation (MICP) by injection of urease positive microorganisms[2]. Monitoring of the consolidation process should ensure that a stable situation is reached.
Liquefaction resistance can also be (temporarily) enhanced by increasing the compressibility of the pore fluid through air/gas injection, electrolysis or chemical/biological gas generation in liquefiable soil layers[33].
Related articles
Further reading
Sumer, B.M. 2009. Liquefaction Around Marine Structures. Advanced Series on Ocean Engineering : Volume 39. World Scientific Publ. Co.
Appendix
This appendix discusses simple mathematical models for the description of transient and residual liquefaction. They are not intended for estimating liquefaction conditions in practice. For the sake of simplicity, we consider waves with a wavelength which is very long compared to the vertical dimensions of the soil dynamic response to the fluctuation wave pressure. We therefore neglect horizontal pore water flow and horizontal soil dilatation. This simplification implies that the model only applies to depths below the seabed surface which are much smaller than the wavelength divided by [math]2\pi[/math].
Transient liquefaction
According to shallow-water wave theory, a propagating sinusoidal wave exerts a fluctuating pressure on the seabed given by
[math]p_{seafloor} (x,t) = p_0 \cos (kx - \omega t) \, , \quad p_0 = \dfrac{ \rho g H}{2 \cosh kh } \, . \qquad (1) [/math]
Symbols: [math]x=[/math] coordinate wave propagation direction, [math]t=[/math] time, [math]g=[/math] gravitational acceleration, [math]\rho=[/math] seawater density, [math]H=[/math] wave height, [math]L=[/math] wavelength, [math]T=[/math] wave period, [math]h=[/math] water depth, [math]k=2 \pi / L =[/math] wavenumber, [math]\omega=2 \pi / T =[/math] radial wave frequency. The vertical coordinate [math]z[/math] is positive and increasing downward with depth; [math]z=0[/math] is the soil surface.
We will not consider any further the [math]x[/math]-dependence of the propagating wave. In the case of an incompressible soil skeleton, an approximate expression of the pore pressure at the seafloor is [math]\quad p'(z,t) = p_0 \cos \omega t \, . \qquad (2)[/math]
In the following we will use the symbols:
- [math]w =[/math] pore water flow velocity in the vertical direction.
- [math]n =[/math] soil porosity, with typical values in the range 0.3 - 0.5 for compacted sediment - loose sediment.
- [math]\beta =[/math] compressibility of pore water and included air (= the ratio of relative volume and decrease pressure increase = inverse of bulk modulus). The water density-pressure relationship is [math]\rho = \rho_0 \exp((p-p_0)/\beta)[/math] and the dependence of [math]\beta[/math] on the air fraction [math]C[/math] is [math]\beta= 5 \, 10^{-10} \, (1-C) + C/p \;[/math]. Typical values in the range 10-9 - 10-6 Pa-1.
- [math]K =[/math] soil permeability (= hydraulic conductivity), relating pore water flow and pressure gradient according to Darcy's law. An empirical estimate for unconsolidated soil is [math]K \approx 10^{-3} \, (g/\nu) \, d_{10}^2[/math], where [math]\nu[/math] is the seawater viscosity and [math]d_{10}[/math] the largest grainsize of the 10% finest sediment fraction.
- [math]\nu[/math], the Poisson's ratio of soil, which is a measure of the transversal expansion divided by the contraction of a sample subjected to vertical compression. It is also related to the internal friction angle [math]\phi[/math] of soil. Typical values are in the range 0.25 - 0.45 (compacted soil - very soft soil).
- [math]G[/math], the [Pa] shear modulus of soil (or modulus of rigidity), measures the soil deformation in response to shear stress, as the ratio of shear stress and shear strain. Typical values or in the range 2.106 - 108 Pa (very soft soil - compacted soil).
Since the bottom skeleton is actually compressible, a correction to the pore pressure [math]p'[/math] has to be applied. The volume [math]V[/math] occupied by the pore fluid will change as the pressure on the seafloor fluctuates. The volume change rate [math]dV/dt[/math] has two components that both are related to the pore pressure [math]p(z,t)[/math]:
- the compression of the pore fluid, [math]\dfrac{dV_1}{dt} = - n V \beta \dfrac{\partial p}{\partial t} \, . \qquad (3)[/math]
- pore water outflow, [math]\dfrac{dV_2}{dt} = -V \dfrac{\partial w}{\partial z} . \qquad (4)[/math]
The pore water velocity is related to the pressure gradient and the soil permeability [math]K[/math] according to Darcy's law, [math]w= - \dfrac{K}{\rho g} \dfrac{\partial p}{\partial z} . [/math]
Therefore, [math]\dfrac{dV_2}{dt} = -\dfrac{K V}{\rho g} \dfrac{\partial^2 p}{\partial z^2} \, . \qquad (5)[/math]
The volume compression implies a change in the volumetric strain [math]\dfrac{d\epsilon}{dt}=\dfrac{1}{V} \big(\dfrac{dV_1}{dt}+\dfrac{dV_2}{dt} \big)[/math]. The change rate of volume strain is thus given by
[math]\dfrac{\partial \epsilon}{\partial t} = - n \beta \dfrac{\partial p}{\partial t} + \dfrac{K}{\rho g} \dfrac{\partial^2 p}{\partial z^2} \, . \qquad (6)[/math]
For small deformations, before the onset of liquefaction, the soil may be considered a poroelastic medium for which Hooke's law applies. Elastic behavior means that the soil resists deformation when subjected to an external stress and recovers its original state when the stress is removed. The volumetric strain rate [math]\partial \epsilon /\partial t[/math] is then linearly related to the effective stress rate [math]\partial \sigma' / \partial t \;[/math] (inter-grain stress), which is the difference between the total stress rate [math]\partial \sigma /\partial t[/math] and the pore pressure rate of variation [math]\partial p / \partial t[/math]:
[math]\dfrac{\partial \epsilon}{\partial t} = -m_v \dfrac{\partial \sigma'}{\partial t} = -m_v \big(\dfrac{\partial \sigma}{\partial t} - \dfrac{\partial p}{\partial t} \big) . \qquad (7)[/math]
The coefficient [math]m_v[/math] is called the compressibility modulus (or coefficient of volume change). For practical applications the compressibility modulus [math]m_v[/math] should be known. As it cannot be measured directly, it is related to other soil characteristics (e.g., [math]G , \nu[/math]) that can de determined with triaxial shear tests. For vertical compaction of homogeneous soils that are not horizontally dilatating, [math]\; m_v = \dfrac{1-2 \nu}{2G(1-\nu)}[/math]. [18] Typical values for compacted sediment - soft sediment are in the range 5.10 - 9-5.10-8 Pa-1.
The total stress [math]\sigma[/math] at soil depth [math]z[/math] fluctuates with the wave-induced pressure fluctuation in the soil. The wave-induced pressure fluctuation [math]\partial\sigma / \partial t[/math] is approximated by [math]\partial p' / \partial t[/math], where [math]p'[/math] is given by Eq. (2).
Using Hooke's law Eq. (7), Eq. (6) can be rewritten as a differential equation from which the wave-induced pore pressure [math]p(z,t)[/math] can be solved:
[math]\Large\frac{\partial p}{\partial t}\normalsize = c_s \Large\frac{\partial p'}{\partial t}\normalsize + c_v \dfrac{\partial^2 p}{\partial z^2} \, , \quad c_s = \Large\frac{m_v}{m_v+n \beta}\normalsize , \quad c_v = \Large\frac{K}{\rho g}\frac{1}{m_v+n \beta}\normalsize \, . \qquad (8)[/math]
The coefficient [math]c_v[/math] is called coefficient of consolidation. The solution of Eq. (8) for a homogeneous soil with vanishing pore pressure variation at large soil depths is given by
[math]p(z,t) = \dfrac{p_0}{1+m} \Big[ \cos \omega t + m \, e^{-\Large\frac{z}{d}\normalsize} \cos ( \omega t + \dfrac{z}{d}) \Big] \, , \quad m = \dfrac{n \beta}{m_v} \, . \qquad (9)[/math]
where [math]\quad d = \Big( \dfrac{2 c_v}{\omega}\Big)^{1/2} = \Big( \dfrac{2 K G}{\rho g \omega} \Big)^{1/2} \, \Big( n \beta G + \dfrac{1 -2 \nu}{2(1-\nu)} \Big)^{-1/2} \, . \qquad (10) [/math]
Values of [math]m[/math] are typically in the range 1-10 for soft sediment. Larger values hold for soils with a high gas content[7].
Values of [math]d[/math] strongly depend on the hydraulic conductivity [math]K[/math] and the pore water compressibility [math]\beta[/math]. Values of [math]d[/math] are typically of the order of a meter for well-drained sediment with a low gas content. In contrast, for fine sediment with low permeability ([math]K \sim[/math] 10-6-10-5 m/s) and significant gas content (order of 1%) values of [math]d[/math] are typically of the order of 10 cm. In both cases [math]d \lt \lt L/(2 \pi)[/math].
The pore pressure gradient just below the seafloor ([math]z \lt \lt d\lt \lt L/2 \pi[/math]) can be approximated by
[math]\Large\frac{\partial p(z,t)}{\partial z}\normalsize \approx - \Large\frac{m \sqrt{2}}{m+1}\frac{p_0}{d}\normalsize \sin ( \omega t +\frac{\pi}{4} ) \, . \qquad (11)[/math]
The tidal phase of the largest upward pressure gradient is [math] \pi /4\omega =T/8[/math] after passage of the wave trough. For transient liquefaction, the wave-induced upward pore pressure gradient near the soil surface under the wave trough (the total pressure gradient measured by piezometers minus the weight of the pore fluid) must be larger than the submerged weight [math]\gamma[/math] of the soil. This condition reads
[math] \dfrac{ \sqrt{2} m}{1+m}\dfrac{p_0}{d} \gt \gamma \, , \quad p_0 = \dfrac{ \rho g H}{2 \cosh(2 \pi h/L)}, \; \gamma = g (\rho_{soil} -\rho) = g (1-n)(\rho_{sed} - \rho) \, , \qquad (12)[/math]
where [math]\rho_{sed}, \, \rho_{soil}[/math] are the median density of the incompressible soil particles and the median density of the soil, respectively.
A numerical example of loosely packed soil of fine sand with a small fraction of silt an clay, saturated with water and including a small fraction (order of 0.5%) of included air, is[34]: [math]n=0.4, \; K=10^{-6} m/s, \; G=10^7 Pa, \; \beta=10^{-7} Pa^{-1}, \; \nu=0.4[/math] ([math]\phi \approx[/math]20°), water depth [math]h = 5 \, m[/math], sea surface waves with period [math]T = 10 \, s[/math] and wavelength [math]L = 70 \, m[/math].
Substitution of the values of the numerical example gives [math]m \approx 2.4 , \; d \approx[/math] 7.5 cm. In the numerical example, transient liquefaction occurs if the wave height [math]H[/math] exceeds 1 m.
Equation (5) does not take into account the gradual build-up of pressure below the soil surface under sustained cyclic loading. The resulting residual liquefaction process is discussed below.
Residual liquefaction
For transient liquefaction, it has been assumed that the volumetric soil strain [math]\epsilon[/math] under wave loading is cyclic. Terzaghi (1925[35]) showed that the pore pressure can increase stepwise under cyclic loading due to gradual compression of the soil skeleton, if the soil is saturated but poorly drained. The simplest assumption is an increase in the total stress [math]\sigma[/math] throughout the soil in proportion to the number [math]N[/math] of wave cycles,[34]
[math]\quad \Large\frac{d \sigma}{dt}\normalsize \propto \Large\frac{p_0}{T}\normalsize , \qquad (13)[/math].
where [math]p_0[/math] is the amplitude of the fluctuating vertical stress on the seafloor given in Eq. (1) and [math]T[/math] the wave period. We call [math]\overline{p}(z,t)[/math] the wave-averaged pore pressure component related to the fluctuating surface water pressure. Instead of Eq. (8) we now have the following equation for [math]\overline{p}(z,t)[/math] :
[math]\Large\frac{\partial \overline{p}}{\partial t}\normalsize= B \dfrac{p_0}{T} + c_v \dfrac{\partial^2 \overline{p}}{\partial z^2} , \qquad (14)[/math]
where [math]B[/math] is a proportionality constant dependent on the soil characteristics, that must be determined experimentally. An approximate solution of Eq. (10) for a homogeneous soil layer of thickness [math]0.1 L \lt D \lt 0.3 L[/math] can be found by assuming a parabolic depth dependence of the pore pressure[34]. The wave-averaged boundary conditions are: for [math]z=0: \; \overline{p}(z,t)=0 \;[/math] (no pore pressure builds up at the seabed surface because pore water can flow out here) and for [math] \; z=D: \; \Large\frac{\partial \overline{p}}{\partial z}\normalsize =0 \;[/math]. The approximate solution is (exact when depth-averaged):
[math]\overline{p}(z,t) \approx z(2D-z)\Large\frac{B p_0}{2 c_v T}\normalsize \Big[ 1 - e^{-\Large\frac{3 c_v t}{D^2}}\normalsize \Big] . \qquad (15)[/math]
The dimensionless coefficient [math]B[/math] represents the rate of pore pressure increase due to soil compaction generated in one wave cycle by a unit applied maximum pressure load. For loosely packed fine sand this rate is of the order [math]B \approx 10^{-3}[/math] [34], while higher values are possible when fractions of silt or clay are present. The coefficient [math]B[/math] has been assumed constant in Eq. (14), but in reality it will gradually decrease during soil compaction. The formula (15) therefore overestimates values of the pore pressure derived from measurements (Fig. 3).
The condition for liquefaction near the seabed surface is
[math]\Large\frac{\partial p}{\partial z} |_{z=0} \normalsize = \Large\frac{BDp_0}{c_v T}\normalsize \ge g(\rho_{soil} -\rho) . \qquad (16)[/math]
In the numerical example, the coefficient of consolidation (Eq. 8) takes the value [math]c_v \approx 0.0018 \, m^2/s[/math]. Taking, for example, [math]B = 10^{-3}[/math] and [math]D = 10 \, m[/math], residual liquefaction occurs for wave heights exceeding 6 m.
References
- ↑ 1.0 1.1 1.2 1.3 Sumer, B.M., Fredsøe, J., Christensen, S. and Lind, M.T. 1999. Sinking/floatation of pipelines and other objects in liquefied soil under waves. Coast. Eng. 38: 53–90 Cite error: Invalid
<ref>tag; name "S99" defined multiple times with different content - ↑ 2.0 2.1 Lin, J., Jeng, D-S., Zhao, H., Gao, Y., Liu, J. and Guo, Y. 2023. Recent advances of seabed liquefaction around the vicinity of marine structures. Ocean Engineering 280, 114660
- ↑ Sumer, B. M. 2014. Liquefaction Around Marine Structures. World Scientific, New Jersey
- ↑ de Groot, M. B., Bolton, M. D., Foray P., Meijers, P., Palmer, A. C., Sandven, R., Sawicki, A. and The, T. C. 2006 Physics of Liquefaction Phenomena around Marine Structures. Journal of Waterway, Port, Coastal, and Ocean Engineering 132: 227-243
- ↑ Klammler, H., Penko, A.M., Staples, T., Sheremet, A. and Calantoni, J. 2021. Observations and modeling of wave-induced burial and sediment entrainment: Likely importance of degree of liquefaction. Journal of Geophysical Research: Oceans 126, e2021JC017378
- ↑ Sassa, S. and Sekiguchi, H. 1999. Wave-induced liquefaction of beds of sand in a centrifuge. Geotechnique 49: 621–638
- ↑ 7.0 7.1 Michallet, H., Mory, M. and Piedra-Cueva, I. 2009. Wave-induced pore pressure measurements near a coastal structure. J. Geophys. Res. 114, C06019
- ↑ Sassa, S., Sekiguchi, H.and Miyamoto, J. 2001. Analysis of progressive liquefaction as a moving-boundary problem. Géotechnique 51, 847–857
- ↑ Sui, T., Yang, M., Peng, L., Chen, J., Zhang, C. and Zheng, J. 2024. Wave-induced residual response and liquefaction of a nonhomogeneous layered seabed. Front. Mar. Sci. 11, 1360641
- ↑ Niu, J.W., Xu, J.S., Dong, P. and Li, G.X. 2019. Pore water pressure responses in silty sediment bed under random wave action. Sci. Rep. 9, 11685
- ↑ Jia, Y., Zhang, L., Zheng, J., Liu, X., Jeng, D-S. and Shan, H. 2014. Effects of wave-induced seabed liquefaction on sediment re-suspension in the Yellow River Delta. Ocean Engineering 89: 146–156
- ↑ Wang, L., Zhang, J., Jeng, D-S., Zhang, Q. and Chen, T. 2023. Experimental study on the dynamic response of a silty seabed under waves. Ocean Engineering 269, 113554
- ↑ Sumer, B.M., Hatipoglu, F., Fredsoe, J. and Sumer, S.K. 2006. The sequence of sediment behaviour during wave-induced liquefaction. Sedimentology 53: 611–629
- ↑ Sui, T., Sumer, B.M., Kirca, V.S.O., Carstensen, S., Zheng, J. and Fuhrman, D.R. 2023. Effect of history of wave exposure on seabed liquefaction. Coastal Engineering 183 (2023) 104307
- ↑ Li, C., Wang, Y., Yu, J.; Qi, W. and Gao, F. 2024. Sequential Evolution of Residual Liquefaction in a Silty Seabed: Effect of Wave-Loading History. J. Mar. Sci. Eng. 12, 750
- ↑ 16.0 16.1 Sui, T., Kirca, V.S.O, Sumer, B.M., Carstensen, S. and Fuhrman, D.R. 2022. Wave-induced liquefaction in a silt and seashell mixture. Coastal Engineering 178, 104215
- ↑ Ishihara, K. and Yamazaki, A. 1984. Analysis of wave-induced liquefaction in seabed deposits of sand. Soils and foundations 24: 85-100
- ↑ 18.0 18.1 Verruijt, A. 2001. Soil mechanics. Delft University Lecture Notes
- ↑ Gratchev, I.B., Sassa, K., Osipov, V.I. and Sokolov, V.N. 2006. The liquefaction of clayey soils under cyclic loading. Eng. Geol. 86: 70–84
- ↑ Zang, J., Jiang, Q., Jeng, D., Zhang, C., Chen, X. and Wang, L. 2020. Experimental Study on Mechanism of Wave-Induced Liquefaction of Sand-Clay Seabed. J. Mar. Sci. Eng. 8, 66
- ↑ Kirca, V., Sumer, B.M. and Fredsøe, J. 2014. Influence of clay content on wave-induced liquefaction, J. Waterw. Port Coast. Ocean Eng. ASCE 140, 04014024
- ↑ Chavez, V., Mendoza, E., Silva, R., Silva, A. and Losada, M.A. 2017. An experimental method to verify the failure of coastal structures by wave induced liquefaction of clayey soils. Coastal Engineering 123: 1–10
- ↑ McAnally, W.H., Friedrichs, C., Hamilton, D., Hayter, E., Shrestha, P., Rodriguez, H., Sheremet, A. and Teeter, A. 2007. Management of Fluid Mud in Estuaries, Bays, and Lakes. I: Present State of Understanding on Character and Behavior. J. Hydr. Eng. 133: 9-22
- ↑ Robillard, D.J. Mehta, A.J. and Safak, I. 2023. Comments on wave-induced behavior of a coastal mud. Coastal Engineering 186, 104400
- ↑ Winterwerp, J.C., de Boer, G.J., Greeuw, G. and van Maren, D.S. 2012. Mud-induced wave damping and wave-induced liquefaction. Coastal Engineering 64: 102–112
- ↑ McAnally, W.H., Friedrichs, C., Hamilton, D., Hayter, E., Shrestha, P., Rodriguez, H., Sheremet, A. and Teeter, A. 2007. Management of Fluid Mud in Estuaries, Bays, and Lakes. I: Present State of Understanding on Character and Behavior. J. Hydr. Eng. 133: 9-22
- ↑ Winterwerp, J.C., Vroom, J., Wang, Z-B., Krebs, M., Hendriks, E.C.M., van Maren, D.S., Schrottke, K., Borgsmüller, C. and Schol, A. 2017. SPM response to tide and river flow in the hyper-turbid Ems River. Ocean Dynamics 67: 559–583
- ↑ Bi, Q., Zhang, Y., Suzuki, Y. and Sivasithamparam, N. 2025. A theoretical model for clay subjected to episodic cyclic loading and reconsolidation. Ocean Engineering 330, 121261
- ↑ Ishihara, K. and Tsukamoto, Y. 2004. Cyclic strength of imperfectly saturated sands and analysis of liquefaction. Proc. Japan Acad. 80 (B): 372-391
- ↑ Zen, K. and Yamazaki, H. 1990. Mechanism of wave-induced liquefaction and densification in seabed. Soils and foundations 30: 90-104
- ↑ Nadim, F. and Kvalstad, T.J. 2007. Risk Assessment and Management for Offshore Geohazards. Procs. First International Symposium on Geotechnical Safety & Risk, Shanghai Tongji University, China
- ↑ Van der Meer, J. and Sigurdarson, S. 2017. Design and construction of berm breakwaters. Advanced Series on Ocean Engineering vol. 40, World Scientific Publ. Co., Singapore
- ↑ Molina-Gomez, F., Viana da Fonseca, A., Ferreira, C. and Caicedo, B. 2024. Insights into the assessment and interpretation of earthquake-induced liquefaction in sands under different degrees of saturation. Earth-Science Reviews 258, 104925
- ↑ 34.0 34.1 34.2 34.3 Verruijt, A. 2006. Offshore soil mechanics. Delft University Lecture Notes
- ↑ Terzaghi, K. 1925. Principles of Soil Mechanics: IV—Settlement and consolidation of clay. Engineering News-Record 95(22): 874-878
Please note that others may also have edited the contents of this article.
|