Fluid mud
Definition of Fluid mud:
Fluid mud is a high-concentration colloidal suspension of fine cohesive sediment particles (< 63 µm with a high percentage of clay particles < 2 µm).
This is the common definition for Fluid mud, other definitions can be discussed in the article
|
Contents
Fluid mud composition
Fluid mud is composed mainly of water and clay- and silt-sized particles. The solid content is dominated by clay minerals with a smaller proportion of silt size minerals such as micas (see Coastal and marine sediments). The mineral composition is location dependent. Cohesiveness is due to electrochemical interparticle bonds and EPS, extracellular polymeric substances exuded by organisms. The fraction of organic matter in marine mud is generally very small, especially in comparison with fresh water environments. The water fraction is very high, more than 90% up to 99.5%. At densities above 1150-1200 kg/m3 (gelling point) the fluidity disappears.
Formation fluid mud layer
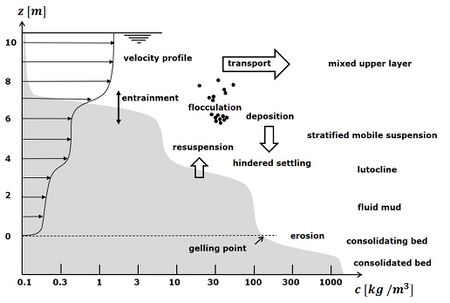
The concentration of fine cohesive sediments in suspension can become very high due to
- Erosion of (partially) consolidated mud deposits by the combined action of strong waves and currents (storm, springtide conditions).
- Convergence of residual fine sediment transport related to tidal asymmetry and estuarine circulation. These processes are a major cause of the formation of a turbidity maximum in estuaries (see Estuarine turbidity maximum).
Settling of fine cohesive sediments is mainly due to floc forming processes, see Flocculation cohesive sediments. A fluid mud layer is formed when flocs of fine cohesive particles settle to the seabed in sufficiently high concentration. This occurs under quiet hydrodynamic conditions (small waves and currents, e.g., neap tide, slack water).
Stirring of unconsolidated mud deposits by wave-induced pressure variations is another process that can contribute to the formation of fluid mud[2]. The high stresses needed in case of advanced consolidation will more likely lead to sediment erosion and suspension rather than to fluidization. A fluid mud layer can be formed when the suspended sediment settles[3].
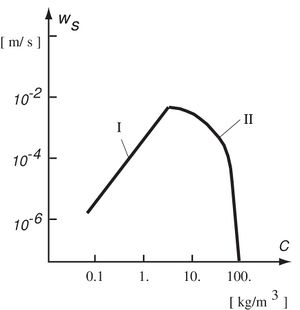
When mudflocs settle, the suspended sediment concentration near the bottom increases. A dense suspension close to the seabed is formed in which further settling is impeded (Fig. 1). There are several theories describing this so-called hindered settling regime[4][5].
When the flocs fill almost all the space, an interconnected matrix of particle bonds is formed in the dense suspension. Sediment settling then becomes impossible. The sediment concentration [math]c[/math] at which the space is completely filled is called the gelling concentration [math]c_{gel}[/math]. The gelling concentration depends on the nature of the flocs. In some situations a value of 40 g/l is found, but generally the value is higher; [math] c_{gel} \approx[/math] 100-200 g/l.
The settling velocity in the hindered settling regime depends on several factors. Contacts with other flocs depend on [math]c/c_{gel}[/math]; floc interaction decreases the settling velocity by a factor [math](1-c/c_{gel})^m [/math]. The weight of the floc in the dense suspension is lower than the weight in clear water by a factor [math](1-c/\rho_s)[/math], where [math]\rho_s[/math] is the density of the suspension. The viscosity of the suspension is increased relative to the clear water viscosity [math]\nu[/math] [8]. This increase amounts to a factor [math](1+2.5 c/c_{gel})[/math], according to experimental evidence. Altogether this leads to the following expression for the hindered settling velocity of fine cohesive sediment:
[math]w_s(c) = w_s(0) \Large\frac{(1-c/\rho_s)(1-c/c_{gel})^m}{1+2.5 c/c_{gel}}\normalsize , \qquad (1) [/math]
where for the exponent the value [math]m=2[/math] is used.
A similar but more elaborated formula was proposed by Camenen[9]; this formula includes the possibility that the flocs do not entirely fill all the space when the gelling point is reached.
Due to hindered settling, the floc settling velocity decreases for concentrations around 10 kg/m[math]^3[/math]. The maximum in the settling velocity curve (Fig. 1) implies that mass settling to the fluid mud layer converges to a concentration exceeding 10 kg/m[math]^3[/math]. The suspended sediment concentration in fluid mud may even reach 250 g/l.
Buoyancy suppresses turbulent exchange between layers of different density, stimulating the formation of a lutocline - a thin transition layer between an upper and a lower layer with low and high suspended sediment concentrations respectively, see Fig. 2. The density difference between the layers is thereby further increased as an auto-enhancing process. According to Winterwerp[10], the density increase may finally exceed the sediment carrying capacity of the lower layer, leading to the collapse of this layer and the formation of a mud bed. Observations in a turbid shallow macrotidal estuary show that unstable shear-induced wave motions on the lutocline (so-called Kelvin-Helmholz instability) can oppose stratification by enhancing vertical mixing[11].
For further details on mud transport, mud bed formation and destruction see Dynamics of mud transport.
Hydrodynamics of fluid mud
As long as the concentration is below the gel point, fluid mud can flow as a viscous near-bed layer, entrained by the flow or by pressure gradients of the overlying water mass. In estuaries, fluid mud layers can be entrained by near-bottom tidal currents over considerable distances without being dispersed over the whole water column[12]. Flow along the bed generates the turbulence needed to prevent the fluid mud from settling.
A seabed covered with fluid mud offers almost no resistance to the flow in the overlying layer. Prandle[14] related the friction coefficient to the mud content of the sediment bed in many UK estuaries; he found evidence for a strong decrease of the friction coefficient with increasing mud fraction. The reduction in flow resistance is mainly due to the suppression of turbulence at the lutocline[15]. The friction factor [math]c_D[/math] can be reduced by a factor 10 or even more.
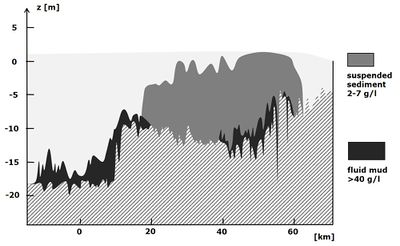
Fluid mud layers are frequently observed at harbour entrances and in artificially deepened navigation channels[16][17], see Siltation in harbors and fairways. Fluid mud layers in estuaries often form during neap tides in the high-water and low-water slack zones where saline and fresh water converge and where fine sediments are trapped, see Fig. 3 and Estuarine turbidity maximum.
Wave damping
Once formed, the fluid mud layer can be maintained by absorbing part of the energy of surface waves. As a consequence, incident waves can be strongly damped by absorption of wave energy in the fluid mud layer. The strong wave damping observed at muddy coasts (for example the coasts of Louisiana, Guiana and Surinam, see Coastal mud belt) is caused by the presence of extensive mud banks[2]. Wave damping is due to energy transfer from the surface wave motion to forced wave motion (same period and wavelength) in the fluid mud layer, where the energy is dissipated by viscous diffusion of fluid momentum. According to an idealized analytical model by Gade (1985[18]), the time scale [math]T_m[/math] for viscous momentum dissipation in the fluid mud layer is given by [math]T_m = \pi h_m^2 / \nu_m[/math], where [math]h_m[/math] is the thickness of the fluid mud layer and [math]\nu_m[/math] the average kinematic viscosity of this layer. The dissipation of the surface wave energy is strongest when the time scale [math]T_m[/math] is of the same order (slightly larger) as the wave period [math]T[/math]. In this situation the wave motion in the fluid mud layer lags the surface wave by about [math]\pi/2[/math]. Values of the viscosity [math]\nu_m[/math] of the fluid mud layer cover a wide range of [math]10^{-4} - 10^{-1} m^2 s^{-1}[/math] depending on the density[19]. Field observations at a mud bank on the Louisiana shelf show that during storm conditions the fluid mud layer contributes little to wave damping, as the lutocline is smoothened by strong turbulence. In contrast, a significant dissipation of wave energy in the mud layer is observed when the storm is waning, associated with a sharp lutocline formed by hindered floc settling and laminar flow in the mud layer[20]. The analysis of Gade suggests that a thin high-viscous layer just above the gelling mud deposit contributes most to wave damping.
Mud gravity flow
Fluid mud can easily slide down a sloping bottom. A slope of about 1% is sufficient. But sliding down an even gentler slope is also possible. This is the case if sufficient external energy is supplied to maintain the mud in colloidal suspension. This could be surface wave energy absorbed in the fluid mud layer, as described above. Fluid mud flows that are maintained in this way are called wave-supported turbidity flows. They can occur during outflow of wave-dominated river deltas into the sea. At tide-dominated deltas, gravity mud flows onto the shelf can occur that remain suspended by tidal energy[2].
With insufficient slope or lack of external energy supply, the fluid mud layer collapses; the mud layer consolidates and becomes part of the soil substrate. Sedimentation is a slow process with a time scale approximately proportional to the square of the layer thickness. Mud gravity flows that feed by taking up sediment from the seafloor are called autosuspended turbidity currents. The density of these mud flows then increases and so does their speed. This type of mud flows can convey mud from shallower to deeper estuarine regions and cause silting up of artificially deepened navigation channels and harbors[2].
Related articles
- Dynamics of mud transport
- Sediment deposition and erosion processes
- Flocculation cohesive sediments
- Estuarine turbidity maximum
- Coastal and marine sediments
- Mud
- Characteristics of muddy coasts
- Coastal mud belt
References
- ↑ Mehta, A.J. 1986. Characteristics of cohesive sediment properties and transport processes in estuaries. In: Estuarine cohesive sediment dynamics. Ed.: A.J.Mehta. Lecture notes coastal and estuarine studies 14, Springer-Verlag, Berlin: 427-445
- ↑ 2.0 2.1 2.2 2.3 McAnally, W.H., Friedrichs, C., Hamilton, D., Hayter, E., Shrestha, P., Rodriguez, H., Sheremet, A. and Teeter, A. 2007. Management of Fluid Mud in Estuaries, Bays, and Lakes. I: Present State of Understanding on Character and Behavior. J. Hydr. Eng. 133: 9-22
- ↑ Winterwerp, J.C., de Boer, G.J., Greeuw, G. and van Maren, D.S. 2012. Mud-induced wave damping and wave-induced liquefaction. Coastal Engineering 64: 102–112
- ↑ Winterwerp, J.C. 2002. On the flocculation and settling velocity of estuarine mud. Cont. Shelf Res. 22: 1339-1360
- ↑ Dankers, P.J.T. and Winterwerp, J.C. 2007. Hindered settling of mud flocs: Theory and validation. Continental Shelf Res. 27: 1893-1907
- ↑ Gust, G. and Walger, E. 1976. The influence of suspended cohesive sediments on boundary-layer structure and erosive activity of turbulent seawater flow. Mar.Geol. 22: 189-206
- ↑ Li, M.Z. and Gust, G. 2000. Boundary layer dynamics and drag reduction in flows of high cohesive sediment suspensions. Sedimentol. 47: 71-86
- ↑ Dyer, K.R., Christie, M.C. and Manning, A. J. 2004. The effect of suspended sediment on turbulence within an estuarine turbidity maximum. Est. Coast. Shelf Sci. 59: 237-248
- ↑ Camenen, B. and Van Bang, D.P. 2011. Modelling the settling of suspended sediments for concentrations close to the gelling concentration. Continental Shelf Res. 31: 106-111
- ↑ Winterwerp, J.C. 2001. Stratification effects by cohesive and non-cohesive sediments. J.Geophys.Res. 106: 22559-22574
- ↑ Tu, J., Fan, D., Lian, Q., Liu, Z., Liu, W., Kaminski, A. and Smyth, W. 2020. Acoustic observations of Kelvin‐Helmholtz billows on an estuarine lutocline. Journal of Geophysical Research: Oceans 125, e2019JC015383
- ↑ Kirby, R. and Parker, W.R. 1983. Distribution and behaviour of fine sediment in the Severn Estuary and Inner Bristol Channel. U.K.Can.J.Fish.Aquat.Sci. 40 (suppl.): 83-95
- ↑ Bertier, C. 2011. Dynamique et suivi du bouchon vaseux dans l’estuaire de la Loire. Séminaire Technique sur le transport sédimentaire: Principes et expériences sur le bassin Ligrien, Vierzon 24 Novembre 2011
- ↑ Prandle, D. 2003. Relationships between tidal dynamics and bathymetry in strongly convergent estuaries. J.Phys.Ocean. 33: 2738-2750
- ↑ Winterwerp, J.C., Manning, A.J., Martens, C., De Mulder, T. and Vanlede J. 2006. A heuristic formula for turbulence-induced flocculation of cohesive sediment. Estuarine, Coastal and Shelf Science 68: 195-207
- ↑ Parker, G., Lanfredi, N.W. and Swift, D.J.P. 1982. Seafloor response to flow in a southern hemisphere sand ridge field: Argentine inner shelf. Sed.Geol.33: 195-216
- ↑ De Jonge, V.N., Schuttelaars, H.M., Van Beusekom, J.E.E., Talke S.A. and De Swart, H.E. 2014. The influence of channel deepening on estuarine turbidity levels and dynamics, as exemplified by the Ems estuary. Estuarine, Coastal and Shelf Science 139: 46-59
- ↑ Gade, H.G. 1958. Effects of a non-rigid, impermeable bottom on plane surface waves in shallow water. J. Mar. Res. 16: 61–82
- ↑ Mehta, A.J. 2023. An Introduction to Hydraulics of Fine Sediment Transport. World Scientific Publ. Co.
- ↑ Traykovski, P., Trowbridge, J. and Kineke, G. 2015. Mechanisms of surface wave energy dissipation over a high-concentration sediment suspension. J. Geophys. Res. Oceans 120: 1638–1681
Please note that others may also have edited the contents of this article.
|