Modelling coastal hydrodynamics
Contents
Introduction
In the analysis of the coastal hydrodynamic processes, modelling (physical, numerical and composite) is often employed to simulate major physical phenomena in the coastal region. Physical models (PM) refer to the use of laboratory models at an appropriate scale ( micro, small, medium and large scale models ) for investigating the relevant process, numerical models (NM) refer to the use of computer codes (commercial, open source, home-made software) and composite models (CM) refer to the integrated and balanced use of physical and numerical models. Hydrodynamic modelling forms the basis for many modelling studies, whether sediment transport, morphology, waves, water quality and/or ecological changes are being investigated. Research is being carried out to improve the representation of tides, waves, currents, and surge in coastal waters.
In the following sections a general outline is given initially with the main characteristics of the coastal hydrodynamics and the associated physical, numerical and composite modelling of the main coastal processes. Phenomena, concepts and insights are presented briefly and modelling of coastal hydrodynamics using physical, numerical and composite models is described. Finally practical applications from the three methodologies are presented together with an extensive list of references.
General outline
Coastal Hydrodynamics and Modelling
Coastal Hydrodynamics
The dynamic processes that exist in the nearshore region are generated by various drivers. Under the influence of these external forces, the fluid motion of the water manifests itself as coastal currents, tides and tidal currents, internal and surface waves, storm surges, tsunamis and others (Horikawa, 1988[1]).
The main difference between coastal waters and deep ocean waters is the presence of two physical constraints (i.e., the sea bottom, at a relatively shallow depth, and the coastline) which somehow determine the motion of the sea water.
The nearshore zone is defined as the region extending from a landward limit associated with storm-wave phenomena (e.g., overwash), to a seaward limit beyond the point where incident waves break, but which depends on the specific context (Horikawa, 1988[1]). Within this zone, several other regions may be distinguished, as shown in figure 1 (Horikawa, 1988[1]). The most relevant of these are the breaker zone, the breaking point, and the surf zone. The former is the zone where incident irregular waves break; the breaking point is where breaking begins and the waves attain maximum height, and the surf zone is defined as the region between the seaward limit of the breaker zone and the area of high turbulence created by the collision of the backrushing water mass and the incoming waves (Horikawa, 1988[1]).
Following Sánchez-Arcilla and Lemos (1990) [2], the relevant phenomena in the surf zone can be classified into four different types:
- Sediment transport and corresponding changes in morphology, with a characteristic time scale of 1 day to 1 month, and a spatial scale between 100 m and 1000 m,
- Currents (non-oscillatory flow), with time scales between 10 minutes and 1 hour, and spatial scales similar to those of sediment transport,
- Organised oscillatory flows (i.e., wind waves, infra-gravity waves), with time scales ranging from 10-1 sec to 10 min, and space scales from 1 to 100 m.
- Random oscillatory flow (turbulence), whose length scales are between 10-3 to 101 sec , and with small (10-4 to 10-1 m) spatial scales.
Broadly spoken, the main features in coastal hydrodynamics are the wind waves, generated by the stress exerted on the ocean surface by the wind. As these waves travel from deep waters into shallower regions, they become more non-linear and dissipative, transferring energy from the peak of the spectrum to higher and lower frequencies. Eventually, the proximity of the sea bottom will induce the breaking of the waves, producing a severe increase in the marine turbulence level, and generating different types of currents, which may extend beyond the surf zone.
However, the study of nearshore hydrodynamics is not an easy task. Wave, current and turbulence scales tend to overlap, thus giving rise to the interaction (to some degree) of these three flow types; since the individual flows are non-linear in nature, their interaction becomes quite complex. The usual procedure followed to derive and understand the governing equations is to decompose all the state variables into contributions from currents, waves and turbulence, and then use time-averaging operators to isolate the desired phenomenon.
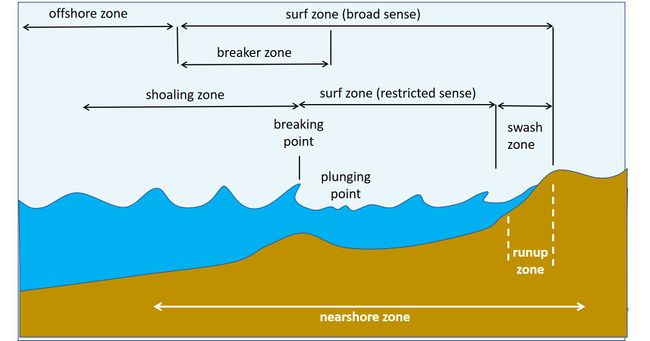
|
| Figure 1: Zone division in the nearshore region (Horikawa 1988[1]) |
Physical Modelling
Physical models and laboratory experiments remain part and parcel of the research methodology because of their many strong points, such as:
- Observability: experiments to investigate mechanisms that are difficult to observe in nature,
- Measurability: experiments to isolate phenomena that are difficult to measure in nature,
- Repeatability: repeated experiments, to investigate the range of inherent uncertainty of phenomena,
- Input control: experiments with various realistic input time series, to assess the predictive capability of numerical models,
- Process control: experiments for simple situations, in order to validate the results of theoretical behaviour analyses,
- Overview: experiments concerning spatial pattern formation (wave fields, morphology, etc.) and requiring synoptic measurements,
- Cost: filling in of field measurements, which are necessarily disperse,
- Robustness: modelling of processes that cannot be modelled numerically, because (unlike numerical models) physical models are basically similar to prototype (especially in facilities that model processes at full scale).
Facilities of various sizes (from large to micro scale) are available for physical modelling of coastal processes. The size of the facility for use depends on the scale and scope of the phenomenon to be modelled. If the prime interest is in the detail of processes the size of the facility may not be critical but the range of the measuring equipment available may be. If the intention is to model flow-boundary interactions over a large area, a large facility is essential so that model scales of 1:10 or 1:100 can be used. Combining detailed process and scale modelling in different facilities can prove very valuable, nesting the results of process studies of critical zones within those from a less detailed, broader scale model.
Large scale models are desirable since the main characteristic parameters can be measured accurately while scaling laws other than Froude scaling (e.g., Reynolds, Weber, etc.) can be accounted for. The scale selection should assure that the dominant forces are well represented. For wave reproduction the capillary forces should play an insignificant role only. Consequently, the wave lengths must not be too sort. A practical lower limit is 0.3 m corresponding to a wave period of 0.4 s. Very small scales also affect the repeatability by which the small-scale waves can be reproduced in the laboratory. In tests where viscous effects are important, attention has to be paid to the Reynolds number. This is related primarily to the coastal structure being tested rather than to the ability to reproduce the waves.
However, micro-models can be an inexpensive alternative for the hydraulic laboratories of Universities and even medium consultancy firms. They can be used as a tool for: the preliminary research of wave-related coastal processes, the development and initial testing of novel ideas, the preliminary design of wave related coastal protection schemes and the testing of alternative design options, the provision of immediate answers and insights to simple coastal engineering problems, the pre-design of large scale physical models.
Physical modelling is more an art than a science when scale and model effects are not fully taken into account in the physical model [3]. Scale effects are related to the inability to scale all relevant forces from prototype to model scale. Model or laboratory effects are related to the inappropriate set-up of the model and the incorrect reproduction of the governing forces, the boundary conditions, the measurement system and the data analysis. Facilities vary widely and are expensive to install and maintain. The correct facility for the application may not be available.
Numerical Modelling
The rapid development of computing technology has generated a large number of models that can be employed in coastal hydrodynamic problems. A variety of coastal models are available and the modelling techniques have become quite mature [4]. The numerical technique can be based on the finite element method, finite difference method , boundary element method, finite volume method and Eulerian-Lagrangian method. The time-stepping algorithm can be implicit, semi-implicit, explicit, or characteristic-based. The shape function can be of the first order, second order, or a higher order. The modelling can be simplified into different spatial dimensions, i.e., a one-dimensional (1D) model, two-dimensional (2D) depth-integrated model, 2D lateral-integrated model, 2D layered model and 3D model.
An analysis of coastal hydraulics and water quality often requires the application of heuristics and empirical experience, and is accomplished through some simplifications and modelling techniques according to the experience of specialists. However, the accuracy of the prediction is to a great extent dependent on boundary conditions, model parameters, and the numerical scheme. The adoption of a proper numerical model for a practical coastal problem is a highly specialized task. These predictive tools inevitably involve certain assumptions and/or limitations, and can be applied only by experienced engineers who possess a comprehensive understanding of the problem domain. This leads to severe constraints on the use of models and large gaps in understanding and expectations between the developers and practitioners of a model.
Composite Modelling
Composite Modelling (CM) is defined as the integrated and balanced use of physical and numerical models [5]. Combining physical modelling and numerical modelling, or Composite Modelling may open up new opportunities for physical modelling, c.q. lead to a new generation of physical modelling infrastructure.
Several ideas and expectations are associated with CM. Firstly, CM allows to get the best out of both Physical Models (PM) and Numerical Models (NM) for a given problem – apply each for that geographical area or for those scales where it performs best, and so lead to an overall better simulation of the relevant processes. Also it may provide more quality (higher accuracy, reduced uncertainty) against the same cost or it may provide the capabilities to model more complex problems which individual PM or NM cannot.
Several authors have discussed CM, though often with slightly different definitions. Barthel and Funke (1989) [6] referred to it as “hybrid modelling” while Oumeraci (1999) [3] proposes a move towards CM, by combining the main strengths of physical and numerical models within a hydro-informatics style of framework. As part of CM, physical model tests would be conducted at a large enough scale to minimise the scale effects, and concentrating on important processes that are not well enough understood to be modelled accurately in a numerical model (i.e. interactions of short-scale and long-scale processes). The results are analysed to increase process understanding of the behavior of the system but are also parameterised so that they can be incorporated into a numerical model that covers a wider area. Kamphuis (2000) [7] discusses the use of various types of modelling and the need to provide well-based quantified results in coastal engineering design. He advocates integration of prototype data, physical and numerical modelling as a further element to improve modelling and design. These elements can essentially complement each other – model simulations provide the continuum information to bridge the gaps in field data, etc.
A key element in integrated models is the computational module (“information manager”) as shown in the following figure.
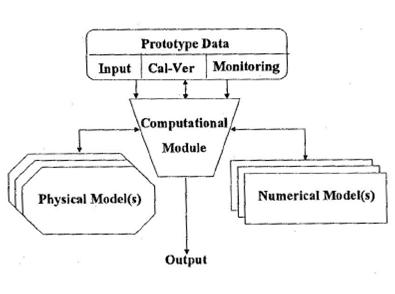
|
| Figure 2: Model integration leading to an integrated model [5] |
The integration of numerical modelling systems, field measurements, experimental laboratory research and theoretical analysis, combined through “calculation or integration modules” will lead to what is called “hybrid modelling” or “composite modelling”. For a problem with different spatial scales, modelling the far field by NM, and the near-field with PM, with proper exchange of information between the two, information exchange and results can be tied together computationally. An extensive range of topics have been identified as well as suited for a composite approach in hydraulic modelling [5].
A decision to apply CM is necessarily preceded by a problem analysis, in the form of the question and answers, in order to estimate a priori the potential benefits of using CM.
The state of the art of the tools for analysing the problem needs to be critically determined first. In different words and for obvious reasons somewhat aggregated we can rephrase that in the questions: Which individual approaches and models are available? Which level of sophistications is required / which model or set of models? Are their strengths and weakness such that they can be satisfactorily applied to analyse the problem given the type of answer required?
The answers to these questions will or should give the information whether it makes sense to use CM: Is one type of model not adequate for analysing and solving the problems? Do physical and numerical models complement each other for this problem? Can different scales be separated in time and / or in space? Can the interfacing of the models and the exchange of data be defined uniquely, in terms of quantified parameters? Can an estimate be given of the uncertainty of the transferred data, so the transfer and effect of uncertainties from model to model can be estimated? Oumeraci (1999) [3], Kamphuis (2000) [7] and Van Os et al. (2004) [8] point out the importance of this interfacing, which needs to be quantified, taking into account uncertainties involved. The above provides the material to formulate a hypothesis on what we expect to gain by CM for this problem, for example in terms of: increased cost effectiveness; improved accuracy; reducing uncertainties; tackling problems that could not reasonably be solved by a single model approach; etc. The outcome of this process is an argued decision on whether or not CM is needed, or whether it is beneficial for modelling the problem at hand.
The advantage of approaching this conscientiously lies in the fact that we systematically build up the various elements into, for instance, an exchangeable and easily accessible library of physical and numerical models and their descriptions or metadata. This will provide updates on their capabilities, usefulness, and track records which is part of Good Modelling Practice.
Phenomena and Concepts
The basic theory of the generation of storm surges and waves by wind is understood in principle [9], although some details still need elucidation. For example, the wind stress is modelled empirically very successfully although the actual process of transfer of momentum and energy from the atmosphere to the sea via wind waves is very complex and not fully understood (Janssen 2004[10]). There are also several interactions between the mean circulation and wind-waves (Peregrine and Jonsson 1983[11]). The propagation of waves in shallow water is dependent on water depth and this means that the total water depth, which includes tide and surge, will affect wave propagation. In fact, the tidal propagation is also modified in the presence of a surge, leading to tide-surge interaction (Wolf 1981[12]), Horsburgh KJ, Wilson C (2007[13]). Waves are modified by the presence of currents generated by tide and surge. They contribute to water level and mean circulation through wave setup and longshore currents, due to radiation stresses in shallow water (see Shallow-water wave theory).
Tides, caused by the gravitational effect of sun and moon, are periodic and very predictable (see Ocean and shelf tides). Surges, on the other hand, are quasi-periodic and caused by meteorological forcing. The most important mechanism for surge generation is wind-stress acting over shallow water. Surges at the coast are produced by Ekman dynamics, behaving as forced Kelvin waves [9]. The size of the surge is proportional to the wind-stress divided by the water depth. The wind-stress is usually taken to be proportional to the square of the wind-speed with a drag coefficient which increases with wind speed accounting for some effect of surface roughness due to waves [14].
Due to transient effects there is also an increase in surge height with wind duration. Surges are, therefore, largest where storms impact on large areas of shallow continental shelves. In deep water, surge elevations are approximately hydrostatic with a 1 hPa decrease in atmospheric pressure giving about 1 cm increase in surge elevation [15]. Surges in the Mediterranean as a whole are likely to be much lower due to the much deeper water. However, they are important in local areas of shallow water, e.g. the Northern Adriatic, where Venice is susceptible to flooding. Some modification is caused by seiching, when winds trigger oscillations at the natural periods of enclosed sea areas, e.g. in the Adriatic the wind tends to trigger the 22-h seiche [9]and its harmonics (11 and 7-h oscillations).
It has long been recognized that in shallow water areas with a large tidal range, the nonlinear effects of tide–surge interaction are important. The peak of the surge in the southern North Sea tends to ‘avoid’ predicted tidal high water, due to the speeding up of the tidal wave propagation in the presence of the deeper water caused by the surge level and by other subtle changes related to bottom friction. Jones and Davies (1998) [16] and Horsburgh and Wilson (2007) [13], among others, have described work on the effects of tide–surge interaction.
Figure 3 illustrates the mechanism by which tide-surge interaction leads to a surge peak on the rising tide.
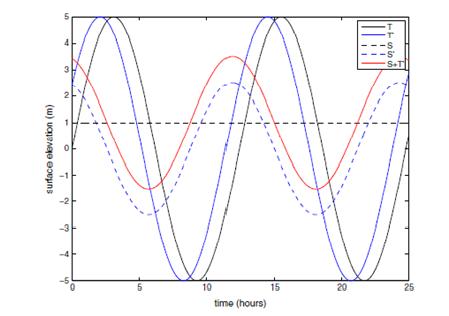
|
| Figure 3: Illustration of tide-surge interaction. Undisturbed tide (predicted tide, T) is solid black line, phase advanced tide (T’) is solid blue line, meteorological surge (S) is dashed black line, tide-surge interaction (S’) is dashed blue line, net residual is solid red line ( Wolf, 2009) [17]. The tidal phase is advanced due to the deeper water caused by the presence of a positive surge level. The difference between the phase-shifted (T0) and undisturbed tide (T) is added to the surge to give the net tidal residual (red line), which has a peak 3 h before predicted high water. |
There are several mechanisms by which waves and the currents and water level associated with tide and surge interact, each component of the combined motion affecting the others [18].
These may be summarized as:
- the effects of water levels and currents on waves and
- the effect of waves on tides and surges.
First, the effect of water levels on nearshore wave transformation are considered. As waves enter shallow water, when the depth is less than half the wavelength, the processes of shoaling and refraction change the wavelength and phase speed but the wave period remains constant (in the absence of currents). As energy propagates at the group velocity, by energy conservation the wave height first decreases then increases (this is because of the group velocity property that it increases first with intermediate depth, only to decrease when the depth becomes shallower [19].
Finally, the energy dissipation processes of breaking and bottom friction start to limit the wave height. If the water depth is modified, by mean sea level changes or tide and/or surge, this will have corresponding effects on wave height. At the coast an increase in water depth will increase the wave height and also the distance to which waves can penetrate inland. Tide and surge currents can affect wave generation, propagation and dissipation. The effect on surface stress is to change the apparent wind and effective fetch. There may also be an enhancement of the wave friction in the bottom stress [20] although Soulsby and Clarke (2005) [21] state this is negligible. Current gradients in the horizontal also cause wave refraction and currents produce a Doppler shift of frequency. In the presence of currents it is the wave action which is conserved rather than wave energy. All these processes are described in more detail in Wolf et al. (1988) [18], Osuna and Wolf (2005) [22] and Ozer et al. (2000) [23].
Waves can affect the mean flow and water level in the nearshore zone through radiation stress causing longshore drift and wave setup (Longuet-Higgins and Stewart 1962[24]). In the surface layer there is a net transport due to waves (Stokes’ drift). Waves may affect the generation of surges by affecting surface roughness. Janssen (1989[25], 1991[26]) introduced the concept of wave stress in which wave age affects the surface roughness and implemented it in the WAM model. Further investigation of this has been carried out by Brown and Wolf (2009) [14]. Waves may enhance the bottom friction experienced by currents in shallow water [20].
Physical, Numerical and Composite Modelling
Physical Models
Wind, waves and swell can be reproduced satisfactorily by a physical model which has to be chosen dependent on various project and site specific parameters like
- model test objectives.
- proposed structure design and rationale behind the proposed structure. These include typical cross sections, detailed drwings of the structure and material related information such as density of material and grain size information.
- bathymetric details of the surrounding area (3D) or the wave approach direction (2D) so that a representative bottom configuration can be constructed. Good quality bathymetric data will assure that wave transformation is well simulated in the model.
- environmental design conditions (wave height, period, water level, wave spectra and wave direction).
- structure performance criteria such as allowable damage level, maximum wave run-up, permissible wave transmission at design wave and water level conditions.
The use of physical models for understanding the impact of water waves is essential for the design of marine structures and assessment of coastal development due to natural causes as well as human intervention. For physical model tests wave characteristics have to be selected like
- The types of the waves to be used (regular, irregular, multi-directional, etc). The selection of wave conditions in the model must be carefully considered in relation to the actual problem.
- The model scale ratios. The largest possible scale for the available experimental facility is generally selected. Other limitations than physical dimensions may play an important role in scale ratio selection (wavemaker capacity, towing speed etc).
- Representative sea states. Wave characteristics from the actual project location shall be the basis for selection of representative sea states for a model test programme. The selection also depends on the application.
- The duration of the time series. In some cases very long testing time is required to obtain enough information to derive design values.
- Free and bound long waves. Any structure or coastline is highly reflective when exposed to long waves. While long waves can often escape to deep water under natural conditions, they are inevitably entrapped in traditional laboratory experiments. Active absorption systems can assist the transparency of offshore boundaries to long waves. Although solved in practice, there are serious practical problems in handling long waves by the wave generator. In shallow water the necessary stroke of the wave generator is very large and may therefore restrict reproduction off extreme sea states at a satisfactory model scale.
- 2D/3D waves. Selection of 2D or 3D wave testing depends on the problem to be investigated, however, a general experience shows that 2D testing is sufficient for a large range of problems. The general lack of good quality directional wave data is also used as a reason not to use 3D testing. In 3D wave basins the treatment of boundary effects such as wave reflection or damping at the boundaries of the wave basin requires larger efforts than in 2D modelling. Monitoring of 3D wave field within the basin can also be problematic. In 3D basins the wave conditions are more inhomogeneous in space than in 2D flumes. Hence, wave conditions in the 3D basins require higher resolution monitoring of wave parameters.
The planning and execution of tests and the measurement and the analysis of laboratory waves are essential parts of physical modelling.
Numerical Models
Storm surges are modelled in detail for a variety of reasons, including most, if not all, of the preceding components for real shorelines as a function of time. One possible reason is the prediction of the 50- or 100-year storm surge at a coastal site for the design water levels for coastal structures or the establishment of hazards and insurance rates for coastal communities. Another purpose, involving real-time modeling, is for hazard mitigation and public safety. Alternatively, the hindcasting of a given historical storm surge may be carried out to determine the nature and extent of the surge or to calibrate and verify a “new” surge model. The latter problem is far easier than the first two, for often data concerning the storm parameters and the wind fields can be obtained. Owing to the lack of long-term water level records or any records at all, statistical surge information is usually unavailable. For actual surge occurrences, often not much data are available except from a few established tide gauge sites and site-specific evidence such as high water levels inside buildings, elevation of wave damage, and other indicators of storm water level.
For any surge model, an adequate representation of a wind field is necessary because the spatial extent of the wind and pressure fields associated with a storm is needed as input. Further, the path of the storm and its correct forward speed are necessary.
Barotropic tides and surges are generally modelled using the ‘shallow-water equations’ since they have very long wavelengths (hundreds of kilometres) compared to the water depth [9]. Heaps (1983) [27], Flather (1981) [28] and Pugh (1987) [29] reviewed earlier work on numerical modelling of storm surges. Limited area models are subject to errors in boundary conditions and tidal models may omit some tidal frequencies, local effects of the tide generating forces and load tide response of the solid Earth. Shum et al.(1997) [30] reviewed ocean tidal models, concluding that all the models agree within 2–3 cm in the deep ocean.
However, tidal models are still inferior to harmonic analysis and prediction for shallow water tides at locations where coastal tide gauge data are available. The tide–surge model predictions reflect this in using the model surge together with harmonic predictions for tides to provide the total water level [31].
A surge model inter comparison exercise (de Vries et al. 1995[32]), using common bathymetry and wind forcing, showed only small differences between models, but highlighted the need for accurate wind-stress since there was a tendency for all models to underestimate the surge. Work on the UK tide–surge model by Williams and Flather (2000) has also shown a need for enhanced wind-stress relative to Smith and Banke (1975[33]) and recently Brown and Wolf (2009) [14] have shown this may be related to wave effects and also nearshore bathymetric resolution.
Numerical wave models can be distinguished into two main categories: phase-resolving models, which are based on vertically integrated, time-dependent mass and momentum balance equations, and phase-averaged models, which are based on a spectral energy balance equation. The application of phase-resolving models, which require 10 ~ 100 time steps for each wave period, is still limited to relatively small areas, O (1 ~ 10 km), while phase averaged models are more relax in the spatial resolution and can be used in much larger regions. Moreover, none of the existing models, phase-resolving or not, considers all physical processes involved.
The more recent research efforts have been focused on the development of unified phase-resolving models, which can describe transient fully nonlinear wave propagation from deep water to shallow water over a large area. In the mean time, significant progress has also been made in simulating the wave-breaking process by solving the Reynolds Averaged Navier Stokes (RANS) equations with a turbulence closure model. These RANS models have also been employed in the studies of wave and structure interactions.
Continuing efforts have been made to construct a unified model for the wave propagation from deep water into shallow water, even into the surf zone. The forerunner of this kind of effort is the ray approximation for infinitesimal waves propagating over bathymetry that varies slowly over horizontal distances much longer than local wavelength. In this approximation, one first finds wave rays by adopting the geometrical optic theory, which defines the wave ray as a curve tangential to the wave number vector. One then calculates the spatial variation of the wave envelope along the rays by invoking the principle of conservation of energy. Numerical discretization can be done in steps along a ray not necessarily small in comparison with a typical wave length. Since the ray approximation does not allow wave energy flux across a wave ray, it fails near the caustics or the focal regions, where neighboring wave rays intersect, diffract and where possibly nonlinearity is important. While ad hoc numerical methods for local remedies are available, it is not always convenient to implement them in practice.
Within the framework of linear wave theory, an improvement to the ray approximation was first suggested by Eckart (1952) [34] and was later rederived by Berkhoff [35] [36], who proposed a two-dimensional theory that can deal with large regions of refraction and diffraction. The underlying assumption of the theory is that evanescent modes are not important for waves propagating over a slowly varying bathymetry, except in the immediate vicinity of a three-dimensional obstacle.
The mild-slope equation in modeling wave propagation from deep water to shallow water is successful, because the vertical profile of the velocity is prescribed “correctly” according to the linear wave theory. The mild-slope equation can be applied to a wave system with multiple wave components as long as the system is linear and these components do not interact with each other.
In applying the mild-slope equation to a large region in coastal zone, one encounters the difficulty of specifying boundary conditions along the shoreline, which are essential for solving the elliptic- type mild-slope equation. The difficulty arises because the location of the breaker cannot be determined a priori. A remedy to this problem is to apply the parabolic approximation to the mild-slope equation [37] [38]. For essentially forward propagation problems, the so called parabolic approximation expands the validity of the ray theory by allowing wave energy “diffuse” across the wave “ray”. Therefore, the effects of diffraction have been approximately included in the parabolic approximation.
The practical application of wave transformation usually requires the simulation of directional random waves. Because of the linear characteristics of the mild-slope equation and the parabolic approximation, the principle of superposition of different wave frequency components can be applied. In general, parabolic models for spectral wave conditions require inputs of the incoming directional random sea at the offshore boundary. The two-dimensional input spectra are discretized into a finite number of frequency and direction wave components. Using the parabolic equation, the evolution of the amplitudes of all the wave components is computed simultaneously. Based on the calculations for all components, and assuming a Rayleigh distribution, statistical quantities such as the significant wave height can be calculated at every grid point. The corresponding nonlinear mild-slope equation and its parabolic approximation have been derived and reported by Kirby and Dalrymple (1983) [37] and Liu and Tsay (1984) [39]. However, one must exercise caution in extending the nonlinear Stokes wave theory into the shallow water; additional condition needs to be satisfied.
Assuming that both non-linearity and frequency dispersion are weak and are in the same order of magnitude, Peregrine (1967) [40] derived the standard Boussinesq equations for variable depth. Numerical results based on the standard Boussinesq equations or the equivalent formulations have been shown to give predictions that compared quite well with field data [41] and laboratory data [42] [43].
Because it is required that both frequency dispersion and nonlinear effects are weak, the standard Boussinesq equations are not applicable to very shallow water, where nonlinearity becomes more important than frequency dispersion, and to deep water, where waves are non-dispersive.
The standard Boussinesq equations written in terms of the depth-averaged velocity break down when the depth is greater than one fifth of the equivalent deep-water wavelength. For many engineering applications, where the incident wave energy spectrum consists of many frequency components, a lesser depth restriction is desirable. Furthermore, when the Boussinesq equations are solved numerically, high frequency oscillations with wave lengths related to the grid size can cause instability. To extend the applications to shorter waves (or deeper water depth) many modified forms of Boussinesq-type equations have been introduced [44] [45] [46]. Although the methods of derivation are different, the resulting dispersion relations of the linear components of these modified Boussinesq equations are similar.
The modified Boussinesq equations are able to simulate wave propagation from intermediate water depth (water depth to wave length ratio is about 0.5) to shallow water including the wave current interaction [47].
Despite of the success of the modified Boussinesq equations in intermediate water depth, these equations are still restricted to weak nonlinearity. As waves approach the shore, wave height increases due to shoaling and waves break on most of gentle natural beaches. The wave-height to water depth ratios associated with this physical process become too high for the Boussinesq approximation. The appropriate model equation for the leading order solution should be the nonlinear shallow water equation. Of course this restriction can be readily removed by eliminating the weak nonlinearity assumption [48] [49]. These fully nonlinear equations can no longer be called Boussinesq-type equations since the nonlinearity is not in balance with the frequency dispersion, which violates the spirit of the original Boussinesq assumption.
In the previous paragraphs all the wave theories have been developed based on the assumption that no energy dissipation occurs during the wave transformation process. However, in most coastal problems the effects of energy dissipation, such as bottom friction and wave breaking may become significant.
The mild-slope equation may be modified in a simple manner to accommodate these phenomena by including an energy dissipation function describing the rate of change of wave energy. The energy dissipation functions are usually defined empirically according to different dissipative processes [50].
Similarly, in the numerical models based on Boussinesq-type equations, adding a new term to the depth-integrated momentum equation parameterizes the wave breaking process. While Zelt (1991) [51], Karambas and Koutitas (1992) [52] and Kennedy et al. (2000) [53] used the eddy viscosity model, Brocchini et al. (1992) [54] and Schaffer et al. (1993) [55] employed a more complicated roller model based on the surface roller concept for spilling breakers. In the roller model the instantaneous roller thickness at each point and the orientation of the roller must be prescribed. Furthermore, in both approximations incipient breaking has to be determined making certain assumptions. By adjusting parameters associated with the breaking models, results of these models all showed very reasonable agreement with the respective laboratory data for free surface profiles. However, these models are unlikely to produce accurate solutions for the velocity field or to determine spatial distributions of the turbulent kinetic energy and therefore, more specific models on breaking waves are needed.
Spectral models entail bringing the full directional and spectral description of the waves from offshore to onshore. These models have not evolved as far as monochromatic models and are the subject of intense research. Examples of such work are Brink-Kjaer (1984[56]), Booij, Holthuijsen, and Herbers (1985) [57], Booij and Holthuijsen (1987) [58], and Mathiesen (1984) [59].
Open source models
Recent models often include the interactions of wave fields with currents and bathymetry, the input of wave energy by the wind, and wave breaking. For example, Holthuijsen, Booij, and Ris (1993) [60] developed the SWAN model, which predicts directional spectra, significant wave height, mean period, average wave direction, radiation stresses, and bottom motions over the model domain. The model includes nonlinear wave interactions, current blocking, refraction and shoaling, and white capping and depth-induced breaking.Numerical modelling of the nearshore circulation system (including rip and longshore currents) permits the study of both onshore and offshore motions as well as longshore motions and can in fact include the influence of rip currents. A variety of models has been developed, for example, Noda (1974[61]), Birkemeier and Dalrymple (1975) [62] , Vemulakonda, Houston and Butler (1982) [63] , Kawahara and Kashiyama (1984) [64], Wu and Liu (1985) [65] and Van Dongeren et al. (1994) [66] . These depth-averaged models in general solve the nearshore circulation field forced by bottom variations, although Ebersole and Dalrymple (1980) [67] examined the case of intersecting wave trains and Wind and Vreugdenhil (1986) [68] addressed the circulation induced between two barriers, pointing out the importance of correctly modeling the lateral shear stresses. The model by Van Dongeren et al. (1994) [66] is quasi-three-dimensional, adding the influence of the undertow on the longshore current, as pointed out by Putrevu and Svendsen (1992) [69]. Madsen, Sorensen, and Schaffer (1997) [70] [71] have shown that an extended Boussinesq wave model can predict surf zone hydrodynamics quite well when a wave-breaking algorithm is included. Averaging the numerical model currents over a wave period yields the “mean” flows of the nearshore circulation system. Chen et al. (1999) [72] compared Boussinesq model results with a physical model of the nearshore circulation on a barred shoreline with rip channels. The numerical model predicts the instabilities in the rip currents as seen in the physical model by Haller et al. (1997) [73].
Most of these nearshore circulation models were developed by finite difference methods, although Wu and Liu (1985) [65] use finite element techniques. Some of these models are being used for engineering work, although it should be pointed out that most of them are very computer intensive and require very small time steps (on the order of seconds) to reach steady-state solutions. This often causes problems when trying to determine the effect of several days’ worth of wave conditions or to predict 1 or 50 years of coastal conditions. Models typically have been developed only for monochromatic (single frequency) wave trains rather than for directional spectra. Several open source codes (Delft3D, [1], TELEMAC, opentelemac.org among others) have been developed recently for modelling coastal hydrodynamics and coastal processes in general.
The Delft3D suite consists of various components to model the particular physics of the water system, such as the hydrodynamics, morphology and water quality. Delft3D allows you to simulate the interaction of water, sediment, ecology and water quality in time and space. The suite is mostly used for the modelling of natural environments like coastal, river and estuarine areas, but it is equally suitable for more artificial environments like harbours, locks, etc. Delft3D consists of a number of well-tested and validated programmes, which are linked to and integrated with one-another. These programmes are: D-Flow, D-Morphology, D-Waves, D-Water Quality, D-Ecology, D-Particle Tracking. The Delft3D Wave component can be used to simulate the propagation and transformation of random, short-crested, wind generated waves in coastal waters which may extend to estuaries, tidal inlets, barrier islands with tidal flats, channels etc.
The Delft3D-Wave module consists of a slightly adapted version of the open source model SWAN and a shell allowing for interaction with Delft3D modules like Delft3D-FLOW and providing additional options for model input like "spiderweb windfields". SWAN was developed by Delft University of Technology (TUD) with support of the Office of Naval Research (ONR). It is managed and maintained by TUD with funding of the Dutch Ministry of Public Works. TUD releases authorized versions of SWAN in the public domain as open source code under the GNU GPL license. The SWAN model is applicable in deep, intermediate and shallow waters and the spatial model grid may cover any model surface area of up to more than 50 km by 50 km.
The added value of Delft3D Wave is the capability of Delft3D Hydrodynamics, Morphology and Waves to perform a so-called online calculation, in which information is transferred from Flow and Morphology to Wave and back again. This online coupling allows for the simulation of complex water systems in which flow-wave (wave currents interaction as well as wave setup) or flow-wave-morphology (effect of radiation stress on sediment transport and seabed changes) are important.
SWAN is a phase-averaged wave model which is less or not applicable in regions where complex phenomena occur within relatively short distances, e.g. near coastal structures or steep sloping beaches, and within harbours. For those areas phase-resolving models are required to obtain more accurate wave predictions. Examples of these models are Boussinesq-type models and Multi-layer models.
In practice Delft3D-Wave (in combination with other modules) is used to transform offshore information such as wind speed statistics to nearshore wave conditions, or more concrete, hydraulic loads on revetments, dune retreat, resulting ship motion, etc. Several models and techniques are required for this transfer, that are coupled in a so-called coastal engineering platform.
Composite Models
Composite Modelling techniques and methodology have been developed within the HYDRALAB-III project of CoMIBBS [5]. Eight composite modelling case studies have conducted in CoMIBBS and recommendations for the use Composite modeling are given.
- Sedimentation bypass for a harbour layout [74] [75],
- Reduction of uncertainties in physical modelling using a numerical error correction technique [76] [77],
- Determination of optimum physical model scale [78],
- Use of a numerical model to design a physical model [74] [75],
- Sensitivity analysis using skill scores [79],
- Composite modelling of scour with parameterized turbulence from a physical model [80] [81] [82],
- Parameterization of physical model results for composite modelling [83] and
- Use of numerical model to overcome 2D physical model constraints [84] [85].
The above cases are presented briefly in the following paragraphs.
- Sedimentation bypass for a harbour layout.
Grunnet et al. (2008) [74] [75] have investigated a harbour placed on an exposed straight coastline and the conditions for maximum bypass of sediment and minimum sedimentation in the harbour mouth by application of composite modelling. Very local physical modelling and larger-scale numerical modelling has been used to support and complement each other. A physical model in a shallow water wave basin was combined with detailed area modelling of the fields of the waves, the current, the sediment transport and the resulting morphological evolution of the bed. The resulting coastline evolution was further simulated by a regional coastline model (a one-line model) based on a littoral drift model. The regional numerical wave model was used for transformation of the wave conditions to the local physical model area. The deposition of sediment in the harbour basin was determined in the physical model. Simulations were made with a coastline model to determine the regional coastline evolution caused by the blocking of the sediment by the harbour and the sedimentation in the harbour basin. - Reduction of uncertainties in physical modelling using a numerical error correction technique
Sandy nearshore bottom profiles profiles can change significantly under severe storms, and it is therefore desirable to take bottom uncertainty into account in physical scale modelling of the (most critical) wave loads on coastal structures. For reasons of complexity and cost, the bottom uncertainty is hardly ever taken into account in physical experiments.
With numerical simulation, this can be done much more flexibly and efficiently, but unfortunately numerical model results for these processes do not yet have the same accuracy as physical scale experiments. Composite Modelling may lead to efficient and accurate determination of the most critical bed form for maximum wave loads, that is, a reduction of the bed uncertainty in usual physical modelling in which merely one or two “well chosen” bed forms are considered.
Van den Boogaard et al. (2009) [76] [77] considered the 1D case of waves over a typical schematised foreshore with a bar, and a low tide terrace (LTT) with unknown length and height (α1, α2), representing the variation in the foreshore profile. They have modelled exactly the same problem with both physical scale model experiments (PM; Scheldt Flume) and with numerical modelling (NM; wave model TRITON). - Determination of optimum physical model scale
The accuracy of modelling wave breaking and sediment transport near the vicinity of coastal structures, through laboratory experimentation, depends very much on the model scale used. A priori, the optimum scale is not known.
Lemos et al. (2009) [78] studied the influence of the physical model scale in (i) the simulation of wave propagation on coastal defences, in particular where the wave breaking phenomena plays an important role, and (ii) the beach profile evolution in front of alongshore structures such as seawalls/revetments, see also (Freire et al., 2009[86]). For wave breaking, they used a NM (COULWAVE) to define the smallest scale to be used in PM tests in a flume that complies with a pre-set level for model scale effects in the wave propagation on a plane slope that ends on a coastal defence. Conversely, scale model results were used to fine-tune the numerical model parameters in order to better describe the flow (especially wave breaking, i.e., wave breaking position and height) at the model geometry. At two laboratory scales, sediment dynamics experiments of the beach profile evolution under storm and mild wave conditions were carried out. These were combined with numerical modelling (NM; LITPROF), which mainly assisted the design of experiments, and helped evaluating its strengths and weaknesses with respect to scaling problems.
The hydrodynamics part focused especially on the complex physical processes involved in the breaking zone. Tests were undertaken using 1:10, 1:20, 1:30, 1:40 and 1:60 model scales, (each case was represented with three different scales), considering different incident wave conditions (regular and irregular waves). The validation of the composite modelling methodology consisted of comparing the scale effect error for wave breaking height and position obtained with the NM for two selected test cases not used in the calibration of the numerical model to the values obtained from the PM. - Use of a numerical model to design a physical model
As part of the CM experiments described by Grunnet et al. (2008) [74] [75], the numerical modelling was also used for the design of the PM including the size of the harbour in the PM, the harbour location between the lateral sides of the basin and the seaward distance to the wave maker in order to ensure that the blocking effect was not causing problems in the PM. In addition, numerical modelling allowed for an initial assessment of the conditions for sediment transport in order to ensure that sediment would in fact be mobilized in the down-scaled laboratory experiment. - Sensitivity analysis using skill scores
Waves and sedimentation around detached breakwater schemes has been modelled using PMs and NMs, which both have their strengths and weaknesses [79]. PM strengths: nonlinear processes; local scour and diffraction; PM weaknesses: scale effects; NM strengths: can model a set of breakwaters without scale effects; NM weaknesses: simplified processes, especially scour, diffraction and representation of the breakwater with no swash-zone processes.
The physical modelling of the detached breakwaters was performed in a coastal wave basin with a single detached offshore breakwater in the centre of a bed of fine sand (d50 = 0.11mm) [87].
Five tests were run of the same case, only with changes to the representation of the water levels, currents and transmission of the breakwater. A laser scanner was used to measure the full physical model bathymetry, which was then transferred to the NM.
Numerical modelling was undertaken using the coastal area model PISCES, which used the finite element flow model TELEMAC, the third generation coastal area wave model SWAN and the sand transport module SANDFLOW to simulate sediment transport, which drove changes in the bathymetry. NM simulations were performed of full-scale versions of the PM, with variations in model set-up. - Composite modelling of scour with parameterised turbulence from a physical model
A good understanding of the processes related to the influence of externally generated turbulence on scour cannot be achieved by applying merely a PM or an NM [80]. A CM approach was therefore designed to systematically investigate the processes involving the externally generated turbulence and its role in scouring. This approach allows to switch on and off the externally generated turbulence in the model runs to single out the effect of the latter, and therefore by doing so, to shed light onto these complex processes.
The key of the CM is the transfer of turbulence determined in the PM to the NM. The NM consists of two numerical codes: a) the hydrodynamic code Ellipsys3D (a 3D RANS solver). Turbulence viscosity is calculated by k-omega SST closure model in the present application and b) a morphologic code comprising three components: (1) for describing the sediment transport process (Engelund-Fredsoe bedload equation, in vectorial form); (2) for describing the sand slide process (the bed avalanches when the slope exceeds the angle of repose); and (3) for describing the mass balance for sediment (at each grid point on bed, to solve bed elevation h). In the PM a half buried spherical object is placed, which is taken to represent an element of a scour protection layer represents the structure [81] [82]. - Parametrisation of physical model results for composite modelling
The topics of interest of this case study are the processes around a vertical slender monopile in waves and the improvement of the knowledge about the dimensions of the developing scour in non-cohesive sediment, such as modelled in Hannover’s large-scale GWK experimental facilities. Combining the best fitting numerical model for scour development and the results of the physical model through some smart CM approach was thought to give further insights. Therefore, a review was made of all general existing tools for CM: numerical modelling, physical modelling, analytical modelling and field measurements [83]. The review showed that data from field measurements are still not available. It also became also clear that no suitable NM is yet available for the simulation of wave induced scour around monopiles. Validation of a recently developed NM against results from the performed large-scale PM experiments) showed unsatisfactory results for irregular waves - Use of numerical model to overcome 2D physical model constraints
The last case considers permeable low crested beach parallel structures (LCS). The interest is in obtaining optimal information on wave heights, currents, water level and bottom evolution around the structure, which is located on a sloping beach (1/15). Water depth at the frontal toe of the structure is 1 m. Two types of structures are employed: one submerged with a freeboard of 0.25 m and one emerged, with a crest height of 0.15 m. The PM was realised in Barcelona’s CIEM large scale flume with mobile bed. The same setup is modelled 1:1 with the morphodynamic model LIMORPH for waves, currents and beach morphodynamics. Nine irregular wave conditions (generated with a Jonswap spectrum) were tested for each structure, corresponding to three different wave heights and three different wave steepness [84] [85].
- Sedimentation bypass for a harbour layout.
The above case studies have shown that, for most of them, both PM and NM can be used to model the processes and provide the essential quantified information on temporal and spatial evolution.
Essential differences have come to light as well. For PMs the so-called similarity principle holds – “the same natural processes occur – essentially we just scale them” [7] [8]. The interactions are not formulated explicitly, nature automatically reproduces them, given the drivers and constraints provided by the modeller.
Therefore, PMs are particularly suited for studies involving non-linear interactions between water, structures and sediment. In these cases the physical model should be run at a large enough scale to minimise scale effects. In some cases, such as with a detached breakwater, it is not possible to run at a scale large enough to have no scale effects and these must be accepted as a limitation of the PM.
In particular for situations where one process is considered, and the range of temporal and spatial scales of interest is limited, well-tested explicit mathematical equations are available, and have been implemented in NM codes, that mimic the dynamic processes of interest, given the provided “drivers and constraints” (geometry, bathymetry, forcing, etc). Characteristic for this is that the scales of interest are also the scales for which the NM is defined. For non-linear processes, the intrinsic interaction across scales when considering larger scales is not necessarily well represented. When explicit interaction descriptions are still hampered by our insufficient understanding the results for the larger scales should be interpreted with caution. The same holds when using the current output from such shorter-term models to drive transport models, if interest is in larger spatial and temporal scales.
The above cases clearly show that applying CM requires an explicit definition of the parameters that will be exchanged, including the quantification of the exchanged amount. This involves parameter location and time, including accuracy and representativity issues. Scales of variation and uncertainty are inherently present, and therefore their transfer from the one model to the other. Aspects such as identifiability and measurability are associated with this. For example, the parameters water level, current components, wave height and wave period are well identifiable quantities, with a large signal to noise ratio.
Assessment of model behaviour and model quality, requires explicit choices for the relevant quantities that need to be evaluated and compared, and quantification of their differences (and which differences in which quantities we find acceptable). This can be done in a quantified manner using a skill score.
Skill scores, such as the Brier Skill Scores are practical and useful to immediately show whether resultants of a model simulation are or are not improved over those of a reference simulation. A variation on this is to use skill scores to choose an optimum PM or NM set-up that has a high skill score but does not require excessive resources to run.
The above reflections emphasize a different aspect of the key element in CM, the need for critical and quantitative assessment of the properties, the strengths and the weaknesses of the PM and NM as well as the strict definition and quantification of the data used to couple the two when they are combined in some form of CM.
For a successful application of CM a careful decision process has to be adopted, which involves questions such as: What models do we use? What is the overall domain in space and time for the problem? What time and space scales will be covered by each model? How to make external forcing consistent for PM and NM? What data to transfer between the models, to provide forcing for the other model? How these are best quantified? What the uncertainty in the data is and how do these uncertainties influence the other model? How do we quantify the results- in terms of which quantities and in which norms? How we evaluate PM and NM data against field data? How can we visualise? How can a sensitivity analysis be conducted (this includes a data exchange protocol)?
A rigorous data exchange protocol is advised in order to be able to assess the influence of the partial modelling elements on each other. Similarly, quantification and evaluation of the results is important in order to show the additional gain or benefit of applying composite modelling.
By systematically addressing these issues and reporting the selections and arguments behind it we make the problem analysis process transparent, and therefore transferable. This is not only important for the particular project itself. Sharing with colleagues internally and externally, and learning from each other will benefit from this as well.
Practical Applications
Physical modelling
Physical modeling of wave overtopping for a steep rubble mound breakwater in Zeebrugge, Belgium (figure 4) has been presented by Geeraerts et al. (2009) [88].

|
| Figure 4: Cross-section of Zeebrugge rubble mound breakwater [88] |
Parametric tests as well as comparison between prototype measurements at the breakwater and their scale reproductions in two laboratories are presented. The objective is to gain information on possible scale and model effects for wave overtopping. The prototype measurements are described together with the resulting dataset of 11 storms where wave overtopping occurred. Scale models and the laboratory measurements are described into detail mentioning similarities and differences to the prototype. Several model effects are identified and special attention is given to wind effects and to the placement pattern of the armour units, respectively. Monte Carlo simulations have been performed to get an idea about the influence of selected model uncertainties. Finally, scale effects are discussed and the influence of model and scale effects for the performed tests is quantified.
Two wave flumes were used for the experiments. The wave flume at Leichtweiss Institute of Braunschweig University (LWI) is 100 m long, 2 m wide and 1.25 m deep. At LWI, waves are generated by a flap type wave paddle that is capable to produce regular and irregular waves (theoretical wave spectra and natural wave spectra) with wave heights up to 0.25 m and wave periods up to 6.0 s for water depths between d=0.60 m and 0.80 m. The wind and wave test facility at Universitad Politécnica de Valencia (UPVLC) is 30 m long, 1.2 m wide and 1.2 m deep. At UPVLC, waves are generated by a piston type wave paddle that is capable to produce regular and irregular waves (theoretical wave spectra and natural wave spectra) with wave heights up to 0.40 m and wave periods up to 3.0 s for water depths at the test area between d=0.35m and 0.65 m.
The model of the Zeebrugge breakwater has been constructed in a 1:30 (Froude) scale. Due to the small scale the core material is too small to reproduce the velocity of water flow correctly. Therefore the method according to Burcharth et al. (1999[89]) which downscales the size of the core material in such way that similar flow velocities in prototype and the model are obtained, was used. This method results in a length scale of 1:20 for the core material.
Two main groups of tests have been carried out: (1) parametric tests on wave overtopping; including variation of measurement analysis and investigation of model effects and (2) reproduction of measured storms.
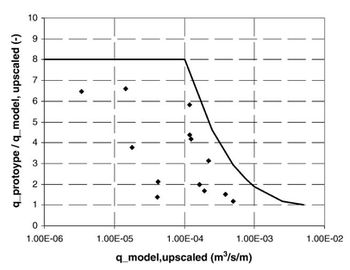
|
| Figure 5: Ratio between prototype overtopping discharge and upscaled model overtopping discharge [88] |
The wind cannot be scaled correctly in a hydraulic model using Froude scaling, however, it has an influence, especially for low overtopping discharges. A qualitative effect has been shown, however no quantitative conclusions were drawn.
Apart from model effects, there is a remaining difference between prototype storms and their model reproductions. It is shown that scale effects can be important and can explain part of these differences. A graph (fig. 5) and a formula (Eq. 1) to estimate the influence of scale and model effects on the overtopping discharge at steep rubble mound breakwaters like the Zeebrugge breakwater have been determined.
Figure 5 gives on the [math]x[/math]-axis the overtopping discharge [math]q[/math] that would be obtained by simply upscaling the model value by Froude law. As a function of this upscaled overtopping discharge, the [math]y[/math]-axis shows the ratio between the measured prototype overtopping discharge and the upscaled model discharge. Hence, an approximation of the influence of scale and model effects on the overtopping discharge for the given structure (and by extension for other steep rubble mound breakwaters) can be made. The graph also shows a conservative curve giving the influence of the scale and model effects as a function of the upscaled overtopping discharge. The curve is represented by the following equations:
| (a) | [math] f_{scale} = 8.0 [/math] | for [math] q \lt 1.10^{-4} m^3/s/m [/math] |
| (b) | [math] f_{scale} = 1.0 + 7.0 (\large\frac{-log(\, q) -2}{2})^2 \normalsize[/math] | for [math] q\lt 1.10^{-2} m^3/s/m \qquad \qquad (1)[/math] |
| (c) | [math] f_{scale} = 1.0 [/math] | for [math] q\gt 1.10^{-2} m^3/s/m [/math] |
Comparisons of average overtopping discharges in large and small scale tests have been performed by Lykke Andersen et al. (2011[90]) for rubble mound breakwaters. Both the small and large scale tests, with a length scale ratio of 5.7, have been performed with fresh water and no wind. The comparison of large and small scale test results led to a new correction procedure to correct for scale effects. The procedure was calibrated to the obtained data in order to establish new guidelines for overtopping scale effects.
Model effects caused by differences in wave height distributions, wave skewness and wave set-up were identified. Because the wave characteristics are very important for small overtopping discharges, it is difficult to separate these model effects from scale effects. Consequently two different normalization methods were used in order to determine the scale effects. The traditional normalization method gives an underestimation of the scale effects as for identical [math]H_{m0}[/math] wave heights the extreme waves are significantly larger in the small scale model. Even using this dimensionless plot, which underestimates the scale effects, larger dimensionless overtopping discharges in the large scale model for the low and normal breakwater height were identified. This shows clearly that a scale effect is present. The difference is most significant in the case of small breakwater crest freeboards (high water level).
A more realistic estimate of the scale effects is found by using [math]H_{1/100}[/math] to make the freeboard and overtopping discharge dimensionless. This analysis method leads to more conservative estimates of the scale effects. Also this analysis shows that the difference between large and small scale overtopping discharges is for identical average overtopping discharge most pronounced in case of small freeboards (high water level). The difference is most significant when the breakwater is low, where more of the overtopping water flows through the armour crest, which gives more influence of drag. The wave steepness also significantly influences the overtopping flow. For high wave steepness the main part of the overtopping water is thrown over as spray when the wave hits and breaks on the slope. For the low wave steepness much more water flows through the armour layer. This has an influence also on the observed differences in overtopping, with larger differences for the low wave steepness. For the high breakwater case the crest berm has, especially for low wave steepness, to be more or less filled with water before overtopping occurs. This reduces the influence of viscosity, and is probably the reason for only identifying small differences in overtopping discharges for this cross-section. The conclusion is that the magnitude of the scale effects is very dependent on the top geometry of the structure.
Numerical modelling
The hydrodynamic aspects of an integrated model system for the prediction of coastal flooding developed as part of the UK Flood Risk Management Research Consortium are presented [91]. The input conditions are offshore wind, waves, tides and surge. Climate models from the Met Office provide boundary conditions for Regional Climate Models (RCM) which in turn provide boundary conditions for wave climate and the continental shelf models of National Oceanographic Centre. These models provide boundary conditions for modelling nearshore waves and water levels due to tides, surge and setup, which are the parameters driving overtopping, inundation and breaching at the coast. The methods are applied to a particular flood event which occurred in Walcott in North Norfolk, UK on 9th November 2007. The coastline at Walcott is orientated approximately northwest-southeast and is prone to attack from the North Sea, especially when the wind blows from the northeast. The danger increases when this wind is combined with a North Sea surge, which can raise the still water level of the sea by up to 2m above the predicted sea level. Such conditions have caused disastrous flooding in the town, as in 1953 and more recently in 2007.
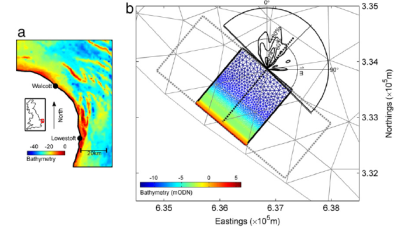
|
| Figure 6: Map of the coastal domain (a) and of the local domain (b) [91]. |
The coupled hydrodynamics-wave system POLCOMS–WAM has been implemented for the NW European shelf region on a computational domain extending from 48-63°N and 12°W to 13°E, with resolution 1/9° latitude by 1/6° longitude (approximately 12x12km). It was used to hindcast the Walcott surge and wave event for November 2007. Wolf (2008, 2009) [92][93] discusses the development of such coupled wave and surge models and the coupling between the POLCOMS and WAM models is described in detail in Osuna and Wolf (2005) [94]. The hydrodynamic model, POLCOMS (POL Coastal Ocean Modeling System), as described in Holt and James (2001) [95], was used to provide the time-evolving tide and surge conditions. The wave model component, WAM (Wave Model), works as a module of POLCOMS, so the wave model uses the same bathymetry and wind information supplied to the hydrodynamic model.
The wave model is a version of the third-generation spectral WAM model [96] which has been extended to be applicable on continental shelf-scale in shallow water [97]. For this application the wave model does not take into account the effect of interaction between waves, water level and currents, although this option is available and may be important in very high-resolution nearshore regions [98].
The model was forced by UK Met Office mesoscale (~12km) atmospheric model winds and pressures, while wave boundary conditions were obtained from a previous coarser implementation of the POLCOMS-WAM model for the NE Atlantic (1° by 1° resolution, extending from 40-70°N and 25°W to 15°E), forced by winds from the European Centre for Medium range Weather Forecasting model. In both the model implementations, the wave model spectral resolution was 24 directions and 25 frequencies. WAM computes the evolution of the 2D spectra, which is then used to estimate the value of a number of integrated parameters (e.g. significant wave height, mean wave direction, zero-crossing wave period, etc.) at every point of the computational domain.
Waves generated offshore and approaching the nearshore are subjected to shallow waters and varying bathymetry, leading to shoaling, refraction and loss of energy either due to bottom friction or to wave breaking. Off Walcott, the tidal and surge regime is large enough to interact with wave propagation. To simulate all these physical processes, the TELEMAC suite [99], containing a shallow water hydrodynamic solver and a wave action conservation equation solver is set up to model inshore water levels and wave spectra for November 2007. This open-source system is also chosen since it allows fine mesh resolution when needed through the FE mesh. A one way nesting procedure with POLCOMS-WAM is implemented, where the output from the coarse model is used to drive the finer model.
To represent the physical processes influencing inshore wave propagation, a numerical approach based on the 3rd generation wave model [100], is adopted. The model takes into account bathymetric wave breaking, bottom friction, nonlinear wave-wave interactions, wind wave generation and white-capping. Offshore waves extracted from POLCOMS-WAM every hour are propagated towards the nearshore using the model in the one-way nesting procedure. The model produces integrated wave parameters and directional wave spectrum at a nearshore location.
Composite modelling
A case which considers permeable low crested beach parallel structures (LCS) is presented [5]. The interest is in obtaining optimal information on wave heights, currents, water level and bottom evolution around the structure, which is located on a sloping beach (1/15). Water depth at the frontal toe of the structure is 1 m. Two types of structures are employed: one submerged with a freeboard of 0.25 m and one emerged, with a crest height of 0.15 m. The PM was realised in Barcelona’s CIEM large-scale flume with mobile bed. The same setup is modelled 1:1 with the morphodynamic model LIMORPH for waves, currents and beach morphodynamics. Nine irregular wave conditions (generated with a Jonswap spectrum) were tested for each structure, corresponding to three different wave heights and three different wave steepness [84].
First, the results of the two model approaches were assessed and compared. The 2DV PM gave good results at the structure front because they reproduce shoaling, refraction, reflection and breaking processes. The PM results at the lee side of the structure are less good, because although it reproduces wave transmission, the PM does not simulate diffraction, longshore currents and sediment transport and it also does not accurately reproduce the water levels there, due to the piling-up effect of water, which gives rise to spurious results for this variable.
The NM did not give good results at the structure front because although it reproduces shoaling, refraction and breaking, it does not simulate reflection. At the lee side of the structure, the NM allowed taking into account diffraction effects, which could not be included in the PM. Moreover, it could give more realistic set-up results in the leeside of the structure, because the NM did not feature the piling-up. However, the NM did not accurately represent the wave transmission. In terms of quality of the process representation for the LCS experiments, the PM and NM are complementary.
Although other possible approaches were analyzed the CM approach existed in selecting the areas where either PM or NM gave the better performance. The assessment of the areas of better performance was process based, i.e. it took into account the physical processes that each model could simulate accurately in each area (in front or behind the structure). In particular, PM results were selected in the front of the structure and NM results at the leeside of the structure, expanding also the domain from 2DV to 2DH or Q3D (Figure 7).
|
| Figure 7: Composite modelling approach. The 2DV PM models the area between the dashed lines and the NM models the whole domain (Q3D approach) [5]. |
Some limitations and constraints observed in 2DV physical models were overcome with the employed approach. Thus, an overall better representation of hydro-morphodynamic conditions around the structure was obtained. This approach was applied successfully to both emerged and submerged permeable low crested structures (Figure 8).
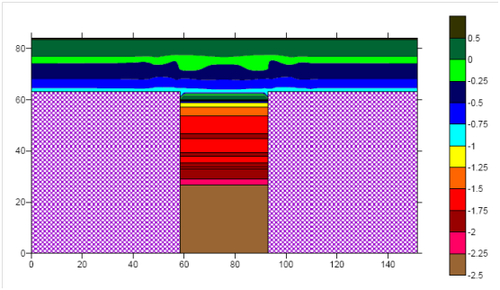
|
| Figure 8: Final bathymetry after 9 tests ( case of emerged structure) [5]. |
It must be stressed that although the main objectives of this composite modelling exercise were achieved (extension of the domain from 2DV to 2DH/Q3D and overcoming of most of the constraints and limitations that the single models have), a number of uncertainties still persisted. Furthermore, some processes could not be assessed or reproduced by this technique. For instance, diffraction was only reproduced by the NM (and is therefore assessed qualitatively only), while the lower resolution of the NM did not allow to reproduce features such as ripples [85].
See also
- Scaling Issues in Hydraulic Modelling
- Hydrodynamic numerical models of wave-structure interaction
- Coastal Hydrodynamics And Transport Processes
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Horikawa, K. (1988) Nearshore dynamics and coastal processes, Univ. of Tokyo Press, Japan, pp 40-88
- ↑ Sánchez-Arcilla, A. and Lemos, C.M. (1990). “Surf-zone Hydrodynamics”. Centro Internacional de Métodos Numéricos de Ingeniería, 310 p.
- ↑ 3.0 3.1 3.2 Oumeraci, H. (1999). Strengths and Limitations of Physical Modelling in Coastal Engineering - Synergy Effects with Numerical Modelling and Field Measurements. Proc. of the Hydralab -Workshop on Experimental Research and Synergy Effects with Mathematical Models, Eds.: K.-U. Evers, J. Grune, A. van Os, Coastal Research Centre, Hannover
- ↑ Chau, KW (2010) Modelling for coastal hydraulics and engineering, Taylor and Francis Ltd., 231 pp.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 5.6 Gerritsen, H., Sutherland, J., Deigaard, R., Sumer, B.M., Fortes, J, Sierra, J-P and Prepernau, U, (2009). Guidelines for Composite Modelling of the Interactions Between Beaches and Structures. Final Report, September, 66 pages, (HYDRALAB-III Deliverable JRA1.4).
- ↑ Barthel, V and E.R. Funke (1989). Hybrid modelling as applied to hydrodynamic research and testing. In: Recent Advances in Hydraulic Physical Modelling, R. Martins (Ed), NATO ASI Series E: Applied Sciences – vol. 165, Kluwer Academic Publishers.
- ↑ 7.0 7.1 7.2 Kamphuis, J.W. (2000). Designing with models. Proceedings of 27th International Conference on Coastal Engineering. Edge, B.L. (Ed) ASCE. pp 19 – 32.
- ↑ 8.0 8.1 Van Os, A.G., Soulsby, R.S. and J. Kirkegaard (2004). The future role of experimental methods in European hydraulic research: towards a balanced methodology. Journal of Hydraulic Research, Vol. 42, No. 4, pp. 341-356.
- ↑ 9.0 9.1 9.2 9.3 Gill AE (1982) Atmosphere-ocean dynamics. Academic Press, London, 662 pp. Goring, D. G. (1978) Tsunamis - the propagation of long waves onto a shelf, Ph.D. dissertation, California Institute of Technology, Pasadena, CA.
- ↑ Janssen, P.A.E.M. (2004) The Interaction of Ocean Waves and Wind, Cambridge University Press, Cambridge, U.K.
- ↑ Peregrine, D. H. & Jonsson, I. G. (1983) Interaction of waves and currents. Rep. MR 83–6. CERC
- ↑ Wolf, J. (1981) Surge‐tide interaction in the North Sea and River Thames, in: Floods due to High Winds and Tides, edited by D. H. Peregrine, pp. 75– 94, Elsevier, New York
- ↑ 13.0 13.1 ) Tide–surge interaction and its role in the distribution of surge residuals inthe North Sea. J Geophys Res 112:C08003.
- ↑ 14.0 14.1 14.2 Brown J, Wolf J (2009) Coupled wave and surge modelling for the eastern Irish Sea and implications for model wind-stress. Continental Shelf Research, 29, 1329-1342.
- ↑ Flather RA (2000) Existing operational oceanography. Coast Eng 41(1–3):13–40.
- ↑ Jones JE, Davies AM (1998) Storm surge computations for the Irish Sea using a three-dimensional numerical model with wave–current interaction. Cont Shelf Res 18:201–251.
- ↑ Wolf, J., 2009. Coastal Flooding – Impacts of coupled wave-surge-tide models. Natural Hazards, 9 (2), 241-260.
- ↑ 18.0 18.1 Wolf J, Hubbert KP, Flather RA (1988) A feasibility study for the development of a joint surge and wave model. P.O.L. report, no 1, 109 pp.
- ↑ Wiegel RL (1964) Oceanographical engineering. Prentice Hall, Englewood Cliffs, New Jersey Williams JA.
- ↑ 20.0 20.1 Grant WD, Madsen OS (1979) Combined wave and current interaction with a rough bottom. J Geophys Res 84(C4):1797–1808.
- ↑ Soulsby RL, Clarke S (2005) Bed shear-stresses under combined waves and currents on smooth and rough beds. Hydraulics research report TR 137.
- ↑ Osuna P, Wolf J (2005) A numerical study on the effect of wave–current interaction processes in the hydrodynamics of the Irish Sea. In: Proceedings of the 5th international conference on ocean wave measurement and analysis. WAVES2005, Madrid, Spain, 3–7 July 2005.
- ↑ Ozer J, Padilla-Hernandez R, Monbaliu J, Alvarez Fanjul E, Carretero Albiach JC, Osuna P, Yu JCS, Wolf J(2000) A coupling module for tides, surges and waves. Coast Eng 41:1–3, 95–124. Peregrine, D.H. (1967) ‘Longwaves on a beach’ J. Fluid Mech., 27, 815-882.
- ↑ Longuet-Higgins, M. S. and Stewart, R. W. (1962) Radiation stress and mass transport in gravity waves, with application to "surf-beats." J. FL Mech. 13, 481-504
- ↑ Janssen, P.A.E.M. (1989) Wave-induced stress and the drag of airflow over sea waves. J. Phys. Oceanogr. 19, 745–754
- ↑ Janssen, P.A.E.M. (1991) Quasi-linear theory of wind wave generation applied to wave forecasting. Accepted for publication in J.Phys.Ocean. 21, 1631-1642
- ↑ Heaps NS (1983) Storm surges, 1967–1982. Geophys J R Astron Soc 74:331–376.
- ↑ Flather RA (1981) Practical surge predictions using numerical models. In: Peregrine DH (ed) Floods due to high winds and tides. Academic Press, London, pp 21–43
- ↑ Pugh DT (1987) Tides surges and mean sea-level. Wiley, Chichester, p 472.
- ↑ Shum CK, Woodworth PL, Andersen OB, Egbert GD, Francis O, King C, Klosko SM, LeProvost C, Li X, Molines J-M, Parke ME, Ray RD, Schlax MG, Stammer D, Tiemey CC, Vincent P, Wunsch CI (1997) Accuracy assessment of recent ocean tide models. J Geophys Res 102(Cll):25173–25194.
- ↑ Flather RA, Williams JA (2004) Future development of operational storm surge and sea level prediction. Proudman Oceanographic Laboratory, Internal Document, No 165, 69 pp.
- ↑ de Vries, H., Breton, M., de Mulder, T., Krestenitis, Y., Ozer, J., Proctor, R., Ruddick, K., Salomon, J. C., and Voorrips, A. (1995) A comparison of 2-D storm surge models applied to three shallow European seas, Environ. Softw., 10, 23–42
- ↑ Smith, S.D., and E.G. Banke (1975) Variation of the sea surface drag coefficient with wind speed. Q.J.R. Meteorol. Soc., 101, 665-673
- ↑ Eckart, C. (1952) ‘The propagation of gravity waves from deep to shallow water’. Circular 20, National Bureau of Standards, 165-173.
- ↑ Berkhoff, J. C.W. (1972). ‘Computation of combined refraction and diffraction’, Proceedings of the 13th International Coastal Engineering Conference, ASCE, 471-490.
- ↑ Berkhoff, J. C.W. (1976). Mathematical models for simple harmonic linear water waves; wave refraction and diffraction. PhD thesis, Delft Technical University of Technology.
- ↑ 37.0 37.1 Kirby, JT, RA Dalrymple (1983). A Parabolic Equation for the Combined Refraction-Diffraction of Stokes Waves by Mildly Varying Topography,” J. Fluid Mechanics, 136, 453–466.
- ↑ Tsay, T.-K. and Liu, P.L.-F. (1982). ‘Numerical solution of water wave refraction and diffraction problems in the parabolic approximation. J. Geophys. Res., 87 (C10), 7932-7940.
- ↑ Liu, P. L.-F. and Tsay, T-K. (1984) ‘Refraction-Diffraction Model for Weakly Nonlinear Water Waves,
- ↑ Peregrine, D.H. (1967) ‘Longwaves on a beach’ J. Fluid Mech., 27, 815-882.
- ↑ Elgar, S. and Guza, R. T. (1985) ‘Shoaling gravity waves: comparisons between field observations, linear theory and a nonlinear model’, J. Fluid Mech., 158, 47-70.
- ↑ Goring, D. G. (1978) Tsunamis - the propagation of long waves onto a shelf, Ph.D. dissertation, California Institute of Technology, Pasadena, CA.
- ↑ Liu, P. L.-F., Yoon, S. B. and Kirby, J. T. (1985) ‘Nonlinear refraction-diffraction of waves in shallow water’, J. Fluid Mech., 153, 185-201.
- ↑ Madsen, P. A., Murray, R. and Sorensen, O. R. (1991) ‘A new form of the Boussinesq equations with improved linear dispersion characteristics’, Coastal Engng, 15, 371-388.
- ↑ Nwogu, O. 1993 ‘An alternative form of the Boussinesq equations for nearshore wave propagation’, J. Waterway. Port,Coast. Ocean Engng, ASCE, 119, 618-638.
- ↑ Chen, Y. and Liu, P. L.-F. (1995) ‘Modified Boussinesq equations and associated parabolic models for water wave propagation,’ J. Fluid Mech., 288, 351-381.
- ↑ Chen, Q., Madsen, P. A., Schaffer, H. A. and Basco, D. R., (1998) ‘Wave-current interaction based on an enhanced Boussinesq approach’, Coastal Engng., 33, 11-39.
- ↑ Liu, P. L.-F. (1994) ‘Model equations for wave propagation from deep to shallow water’, in Advances in Coastal and Ocean Engineering, 1, 125-158.
- ↑ Wei, G., Kirby, J. T.,Grilli, S. T. and Subramanya, R. (1995) ‘A fully nonlinear Boussinesq model for surface waves. Part I Highly nonlinear unsteady waves,’ J. Fluid Mech., 294, 71-92.
- ↑ Dalrymple, R.A., Kirby, R.T. and Hwang, P.A. (1984). ‘Wave diffraction due to area of energy dissipation.’ J. Waterway, Port, Coastal, and Ocean Engineering, ASCE., 110 (1), 67-79.
- ↑ Zelt, J. L. (1991) ‘The run-up of non breaking and breaking solitary waves’, Coastal Engng, 15, 205-246.
- ↑ Karambas, Th. V. and Koutitas, C. (1992). ‘A breaking wave propagation model based on the Boussinesq equations.’ Coastal Engng, 18, 1-19.
- ↑ Kennedy, A.B., Chen, Q., Kirby, J.T. and Dalrymple, R.A. (2000). ‘Boussinesq modeling of wave transformation, breaking and runup, I: 1D.’ J. Waterway, Port, Coastal, and Ocean Engineering, ASCE, 126 (1), 39-48.
- ↑ Brocchini, M., Drago, M. and Ivoenitti, L. (1992). ‘The modeling of short waves in shallow water: Comparison of numerical model based on Boussinesq and Serre equations.’ Proc. 23rd Intnl. Conf. Coastal Engng. ASCE. 76-88.
- ↑ Schaffer, H.A., Madsen, P.A. and Deigaard, R.A. (1993). ‘A Boussinesq model for waves breaking in shallow water.’ Coastal Engng, 20, 185-202.
- ↑ Brink-Kjaer, 0. (1984) Depth-Current Refraction of Wave Spectra", Proceedings of Symposium on Description and Modelling of Directional Seas, Tech. Univ. of Denmark, paper No.C7
- ↑ Booij, N., L.H. Holthuijsen, and T.H.C. Herbers (1985) A Numerical Model for Wave Boundary Conditions in Port Design. Proc. Intl. Conf. Numerical and Physical Modeling of Ports and Harbours,” BHRA, Birmingham, 263–268.
- ↑ Booij, N., and L.H. Holthuijsen (1987). Propagation of Ocean Waves in Discrete Spectral Wave Models. J. Computational Physics, 68, 307–326.
- ↑ Mathiessen, M. (1984). Current-Depth Refraction of Directional Wave Spectra. Symp. Description v and Modeling of Directional Seas, Tech. Univ. Denmark
- ↑ Holthuijsen, L.H.,N. Booij, and R.C. Ris (1993) A Spectral Wave Model for the Coastal Zone, Proc. 2nd Intl. Symp. Ocean Wave Measurement and Analysis, ASCE, NewOrleans, 630–641.
- ↑ Noda, E.K. (1974) Wave induced nearshore circulation. J. Geophys. Res. 79, 4097 – 4106
- ↑ Birkemeier,W.A., and R.A. Dalrymple (1975). Nearshore Water Circulation Induced by Wind and Waves. Proceedings of Modeling 75, ASCE, San Francisco.
- ↑ Vemulakonda, S.R., J.R. Houston, and H.L. Butler (1982). Modeling of Longshore Currents for Field Situations. Proc. 18th Intl. Conf. Coastal Eng., ASCE, Cape Town.
- ↑ Kawahara, M., and K. Kashiyama (1984). Selective Lumping Finite Element Model for Nearshore Currents. Int. J. Numerical Methods Fluids, 4, 71–97.
- ↑ 65.0 65.1 Wu, C.-S., and P.L.-F. Liu (1985). Finite Element Modelling of Nonlinear Coastal Currents. J. Waterway, Port, Coastal and Ocean Eng., ASCE, 111, 2, 417–432.
- ↑ 66.0 66.1 Van Dongeren, A.R., F.E. Sancho, I.A. Svendsen, and U. Putrevu (1994) SHORECIRC: A Quasi 3-D Nearshore Model. Proc. 24th Intl. Conf. Coastal Eng., ASCE, Kobe.
- ↑ Ebersole, B.A., and R.A. Dalrymple (1980). Numerical Modelling of Nearshore Circulation. Proc. 17th Intl. Conf. Coastal Eng., ASCE, Sydney.
- ↑ Wind, H.G., and C.B. Vreugdenhil (1986). Rip-current Generation Near Structures. J. Fluid Mechanics, 171, 459–476.
- ↑ Putrevu,U., and I.A. Svendsen (1993). Shear Instability of Longshore Currents: A Numerical Study. J. Geophys. Res., 97, C5, 7283–7303.
- ↑ Madsen, P.A.,O.R. Sorensen, and H.A. Schaffer (1997a). Surf Zone Dynamics Simulated by a Boussinesq Type Model. Part I. Model Description and Cross-shore Motion of Regular Waves. Coastal Eng., 32, 255–287.
- ↑ Madsen, P.A.,O.R. Sorensen, and H.A. Schaffer (1997b). Surf Zone Dynamics Simulated by a Boussinesq Type Model. Part II. Surf Beat and Swash Oscillations for Wave Groups and Irregular Waves. Coastal Eng., 32, 287–319.
- ↑ Chen, Q., R.A. Dalrymple, J.T. Kirby, A. Kennedy, and M.C. Haller (1999). Boussinesq Modelling of a Rip Current System. J. Geophys. Res., 104, C9, 20,617–20, 638.
- ↑ Haller, M.C., R.A. Dalrymple, and I.A. Svendsen (1997). Rip Channels and Nearshore Circulation. Proc. Waves ’97, ASCE.
- ↑ 74.0 74.1 74.2 74.3 Grunnet, N., Lohier, S. and Deigaard, R. (2008). Study of sediment bypass at coastal structures by composite modelling. Proc. 31st Int. Conference on Coastal Engineering (ASCE), Hamburg, Germany,. World Scientific, Volume 2, pp 1876 - 1887.
- ↑ 75.0 75.1 75.2 75.3 Grunnet, N., Lohier, S., Deigaard, R., Broker, I. and Huiban, M.(2008) Modelling of Bypass of Sediment at Harbours. Littoral 2008: 9th International conference, Venice, Nov. 2008, 8 pp.
- ↑ 76.0 76.1 Van den Boogaard, Henk; Herman Gerritsen, Sofia Caires, Marcel van Gent (2009). Composite modelling by applying an inverse technique in analysing interactions between beaches and structures. Proc. 8th Int. Conf on Hydroinformatics, Concepcion, Chile, 12-16 January, 2009, paper 188a178, 10 pages.
- ↑ 77.0 77.1 Van den Boogaard, Henk; Herman Gerritsen, Sofia Caires, Marcel van Gent (2009b). Wave attack on sea defences – potential benefits of a composite modelling approach. Proceedings 33rd IAHR Congress, Vancouver, August 2009, paper 10443, pp. 1006-1013.
- ↑ 78.0 78.1 Lemos R., Fortes., C. J.E.M., Gil L., Neves M.G. (2009) The influence of the geometric scale model on the physical modelling of the wave propagation and breaking in a flume. Journal of Coastal Research, SI 56, pp 583 – 592.
- ↑ 79.0 79.1 Sutherland, J. and Obhrai, C., 2009. CoMIBBS composite modelling report. HR Wallingford Report TR173, which is also HYDRALAB-III Report JRA1-08-05.
- ↑ 80.0 80.1 Sumer, B. M. (2007). Mathematical modeling of scour: A review. J. Hydraulic Research, Vol 45, Issue 6, pp.723-735.
- ↑ 81.0 81.1 Dixen, M. (2008). Interaction between seabed and scour protection, Ph.D. Thesis, Technical University of Denmark Department of Mechanical Engineering, Coastal, Maritime and Structural Engineering Section.
- ↑ 82.0 82.1 Dixen, M., Sumer, B.M. and Fredsoe, J. (2010). Flow and scour around a half-buried sphere. In preparation.
- ↑ 83.0 83.1 Prepernau, U., Grune, J., Schmidt-Koppenhagen, R., Wang, Z. and Oumeraci, H. (2008): Large-scale model tests on scour around slender monopole under livebed conditions, Proc. of the Second International Conference on the Application of Physical Modelling to Port and Coastal Protection (CoastLab08), 2-5 July, Bari, Italy pp 215 - 224.
- ↑ 84.0 84.1 84.2 Sierra, J.P., Gironella, X., Sanchez-Arcilla, A., Sospedra, J., Alsina, J.M. (2007). Hybrid modelling of scouring-deposition in front of a coastal structure. Journal of Coastal Research, SI 50, 364-368.
- ↑ 85.0 85.1 85.2 Sierra, J.P., Gironella, X., Alsina, J.M., Oliveira, T.A.C., Caceres, I., Mosso, C., Mestres, M. (2009). Physical and numerical modeling of beach response to permeable low-crested coastal structures. Journal of Coastal Research, SI 56, 1065 - 1069.
- ↑ Freire, P., Sancho, F., Oliveira, F.S.B.F. (2009). Composite modelling of sediment dynamics for propagating waves reaching coastal defences. In: 2nd Int. Conf. Application of Physical Modelling to Port and Coastal Protection (L. Damiani, M. Mossa, eds.) IAHR, Madrid, pp. 125-135
- ↑ Obhrai, C. and Sutherland, J., (2009). CoMIBBS physical model report. HR Wallingford Report TR172, Release 2.0, February 2009. Also HYDRALAB-III Report JRA1-08-06.
- ↑ 88.0 88.1 88.2 Geeraerts, J.; Kortenhaus, A.; Gonzalez-Escriva, J.A.; De Rouck, J.; Troch, P. (2009). Effects of new variables on the overtopping discharge at steep rubble mound breakwaters - The Zeebrugge case Coast. Eng. 56(2): 141-153.
- ↑ Burcharth, H.F., Liu, Z., Troch, P., (1999) Scaling of core material in rubble mound breakwaters model test. In: Proc. of the 5th International Conference on Coastal Engineering in Developing Countries (COPEDEC), Capetown, pp. 1518–1528
- ↑ Lykke Andersen, T., Burcharth, H.F., Gironella, X. (2011) Comparison of new large and small scale overtopping tests for rubble mound breakwaters, Coastal Engineering, 58, 351-373
- ↑ 91.0 91.1 Chini, N. and Stansby, P.K. (2012) Extreme values of coastal wave overtopping accounting for climate change and sea level rise. Coastal Engineering, 65, 27-37.
- ↑ Wolf, J., 2008. Coupled wave and surge modeling and implications for coastal flooding. Advances in Geosciences. 17, 1-4.
- ↑ Wolf, J., 2009. Coastal Flooding – Impacts of coupled wave-surge-tide models. Natural Hazards, 9 (2), 241-260.
- ↑ Osuna P, Wolf J (2005) A numerical study on the effect of wave–current interaction processes in the hydrodynamics of the Irish Sea. In: Proceedings of the 5th international conference on ocean wave measurement and analysis. WAVES2005, Madrid, Spain, 3–7 July 2005.
- ↑ Holt, J.T., James I.D., (2001). An s coordinate density evolving model of the northwest European continental shelf: 1, Model description and density structure. Journal of Geophysical Research, 106(C7), 14,015−14,034.
- ↑ Komen GJ, Cavaleri L, Donelan M, Hasselmann K, Hasselmann S, Janssen PAEM (1994) Dynamics and modelling of ocean waves. Cambridge University Press, Cambridge, p 532.
- ↑ Monbaliu, J.; Padilla-Hernandez, R.; Hargreaves, J.C.; Carretero Albiach, J.C.; Luo, W.; Sclavo, M.; Günther, H. (2000). The spectral wave model, WAM, adapted for applications with high spatial resolution Coast. Eng. 41(1-3): 41-62
- ↑ Brown, J.M., Bolaños, R., Wolf, J., (2011). Impact assessment of advanced coupling features in a tide-surge-wave model, POLCOMS-WAM, in a shallow water application. Journal of Marine Systems (in press).
- ↑ Hervouet J-M., (2007). Hydrodynamics of free surface flows modelling with the finite element method. Wiley, 342pp.
- ↑ TOMAWAC Benoit, M., Marcos, F. and Becq, F., (1996). Development of a third generation shallow water wave model with unstructured spatial meshing, 25th international Conference on Coastal Engineering, Orlando, pp. 465-478.
Please note that others may also have edited the contents of this article.
|