Tidal asymmetry and tidal inlet morphodynamics
This article describes the physical processes responsible for tidal wave deformation in shallow coastal inlet systems – tidal lagoons and estuaries. A qualitative discussion is given of the mutual interaction between tidal asymmetry generation and morphological development of these systems, which is generally referred to by the term self-organizing morphodynamics. This article is largely based on the book Dynamics of Coastal Systems [1].
Contents
- 1 Tidal wave skewness
- 2 Tidal wave deformation in the absence of friction
- 3 Tidal wave deformation in the presence of friction and intertidal areas
- 4 Morphology of shallow tidal basins with small river inflow
- 5 Tidal wave deformation in a converging channel
- 6 Morphology of estuaries with tidal rivers
- 7 Symbols
- 8 Related articles
- 9 References
- 10 Appendix
Tidal wave skewness
Tides result from the response of ocean water bodies to the attractive gravitational forces of sun and moon. Tidal motion in the oceans can be described by a number of sinusoidal components, because earth's rotation and the relative movements of earth, sun and moon have a cyclical character, see the article Ocean and shelf tides. The semidiurnal lunar tide (M2) is usually the dominant component, in which case the ocean tide can be described fairly accurately with a single sine function.
Ocean tidal waves are distorted when they propagate into shallow coastal waters. Here the term tidal wave distortion is to be understood as a systematic (long-term averaged) difference between the periods of rising and falling tide, also called tidal asymmetry. We will use the term positive duration asymmetry for tides with a longer fall and shorter rise and negative duration asymmetry for tides with a shorter fall and longer rise. Nonlinear hydrodynamic processes, which are insignificant in the deep ocean, become important when the tidal range exceeds a small fraction of the mean water depth. In other words, non-linear terms become important in the equations describing the propagation of tidal waves. For example, quadratic terms introduce tidal components at twice the frequency of the semidiurnal lunar M2 tide. This so-called M4 tidal component can strengthen the flood current and weaken the ebb current, or vice versa. A quantitative measure of tidal asymmetry is the so-called 'skewness' parameter [math]\gamma[/math],
[math]\gamma = \sqrt{nT} \, \Big(\int_0^{nT} u^2(t) dt \Big)^{-3/2} \int_0^{nT} u^3(t) dt , \qquad (1)[/math]
where [math]u(t)[/math] is the tidal velocity, [math]T[/math] the period of the semidiurnal tide and [math]n[/math] a large integer. If [math]u(t) \gt 0[/math] for flood flow, then a positive value of [math]\gamma[/math] implies flood dominance and a negative value ebb dominance.
A non zero value of [math]\gamma[/math] has consequences for the long-term average transport of sediment, because the dependence of the sediment transport [math]q_s[/math] on the flow strength follows the approximate formula
[math]q_s \propto u |u|^{\alpha} , \qquad (2)[/math]
where the exponent [math]\alpha[/math] can take values between 2 and 4 (see e.g., Sand transport). A positive (negative) skewness implies net upstream (downstream) tide-induced sediment transport.
Because in practice the tidal elevation [math]\zeta (t)[/math] is measured more easily than the flow velocity [math]u(t)[/math], tidal asymmetry is usually related to the skewness coefficient [math]\gamma_1[/math], which is the same as Eq. (1) with [math]u(t)[/math] replaced by [math]\partial \zeta / \partial t[/math]. The skewness coefficient [math]\gamma_1[/math] is a measure of the average difference between periods of falling tide and rising tide. The interpretation of [math]\gamma_1[/math] is similar to the interpretation of [math]\gamma[/math] in situations where tidal flow is mainly driven by the water level slope [math]\partial \zeta / \partial x[/math] (Nidzieko, 2010[2]).
Linear ocean tides naturally have nonzero skewness. The skewness would be zero if the frequencies of the tidal components were random numbers. However, this is not the case; they are all multiples of a limited number of fundamental frequencies. For example, the sum of the frequencies of the two main diurnal tidal components K1 and O1 is equal to the frequency of the M2 tide. Any linear superposition of the M2, K1, and O1 tides therefore produces nonzero skewness according to Eq. (1). Most linear superpositions of tidal frequencies thus breach ebb-flood asymmetry and produce net tide-induced sediment transport. The strongest net transport is produced by the triplet M2, K1, O1. Although this was known for a long time (Doodson, 1921)[3], it has received renewed attention more recently due to the observations and analyses of Hoitink et al. (2003)[4] and Zhang et al. (2018 [5]). A world map showing ocean regions with different tidal asymmetry was published by Song et al. (2011[6]), based on tidal constants derived from the TPXO7-ATLAS[7]. This map is shown in the article Ocean and shelf tides#Asymmetric ocean tides. Important asymmetric tides (with either positive or negative skewness [math]\gamma_1[/math]) occur mainly in regions where tides have a mixed character, with comparable magnitudes of diurnal and semidiurnal tidal components.
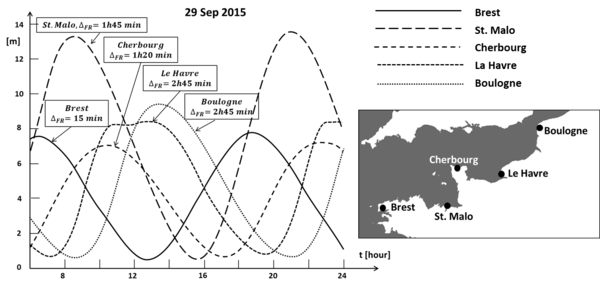
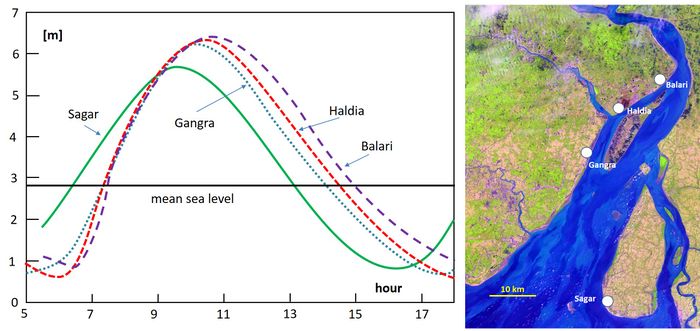
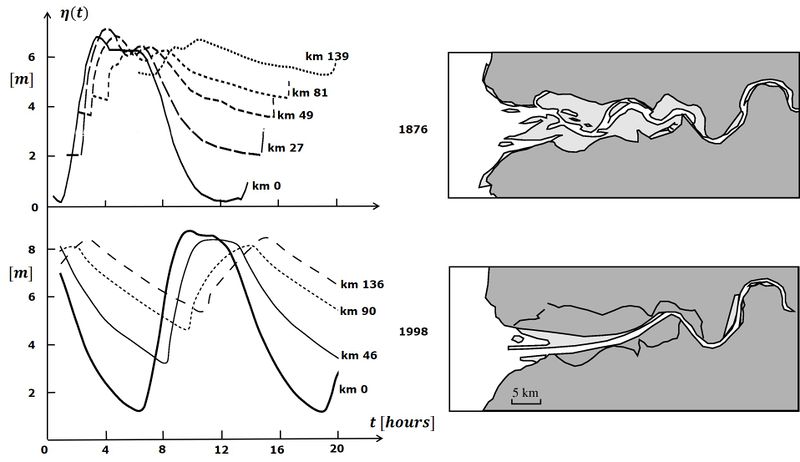
Although the asymmetry of ocean tides can be significant, tidal asymmetry can become much stronger due to the generation of shallow-water overtides in shallow coastal areas with a large semidiurnal tidal range (dominated by M2). The distortion of the tide can be so strong that the durations of rising tide and falling tide become very different and that a large difference arises between the peak flow velocities of flood and ebb. Often the duration of rising tide is much shorter than the duration of falling tide. The asymmetry of the tidal wave increases when propagating up-estuary. This is illustrated in Fig. 1 for the Hooghly estuary. In the most extreme case, the duration of tidal rise becomes so short that a hydraulic jump develops at the front of the tidal wave. The front of the tidal wave appears as a propagating wall of water, a so-called tidal bore, as explained in the article Tidal bore dynamics.
In the following we review the major nonlinear processes involved in initiating shallow-water tidal distortion. We focus on asymmetry generated by the interaction of tides with topographic characteristics. Like most analytical studies of overtide generation, we consider estuaries and tidal rivers with simple one-dimensional geometries. The influence of channel curvature, secondary channels or local channel constrictions on tidal asymmetry are ignored. Asymmetries related to density gradients or wind-driven currents are also left out of consideration. A discussion of these processes can be found in the articles Morphology of estuaries, Seawater intrusion and mixing in estuaries, Estuarine circulation and Estuarine turbidity maximum.
This article contains many formulas. At the end of the article a list of symbols used is presented.
Tidal wave deformation in the absence of friction
The distortion of the tide described above is related to a difference in propagation speed of the high-water crest of the tidal wave and the low-water trough. This difference already occurs when the water depth below the wave crest is slightly greater than the water depth below the wave trough. This can be easily demonstrated for a tidal wave that propagates in [math]x[/math]-direction with time [math]t[/math] in deep water with little loss of friction. The most simple geometry is an infinite prismatic channel. The mean (tide-averaged) channel depth is called [math]h[/math] (constant), the tidal elevation is called [math]\zeta(x,t)[/math], the total instantaneous water depth [math]D(x,t)=h+\zeta(x,t)[/math] and the cross-sectionally averaged velocity [math]u(x,t)[/math].
In the absence of friction, the tidal equations for mass and momentum read:
[math]\Large\frac{\partial \zeta}{\partial t}\normalsize +\Large\frac{\partial((h+\zeta)u)}{\partial x}\normalsize=0 ; \qquad \Large\frac{\partial u}{\partial t}\normalsize + u \Large\frac{\partial u}{\partial x} \normalsize + g \Large\frac{\partial \zeta}{\partial x}\normalsize = 0 , \qquad (3)[/math]
where [math]g[/math] is the gravitational acceleration. Overtides are due to the nonlinear terms [math]\partial(\zeta u) / \partial x [/math] and [math] u \partial u / \partial x[/math]. The quadratic nature of these terms implies that the first and most important overtide (M4) has twice the frequency of the M2 tide.
The tidal equations (3) can be cast in the form of two characteristic equations
[math]\Large\frac{d}{dt}\normalsize[u(x(t),t) +2c(x(t),t)] = 0, \; \Large\frac{d x(t)}{dt}\normalsize = u(x(t),t) + c(x(t),t) ; \qquad \Large\frac{d}{dt}\normalsize[u(x(t),t) - 2c(x(t),t)] = 0, \; \Large\frac{d x(t)}{dt}\normalsize = u(x(t),t) - c(x(t),t) , \qquad (4)[/math]
where [math]c = \sqrt{gD}[/math]. The first equation represents a wave propagating in positive [math]x[/math]-direction and the second a wave propagating in negative [math]x[/math]-direction. From these equations it follows that the speed at which the wave crest propagates in positive [math]x[/math]-direction is given by
[math]\Large\frac{dx^+}{dt}\normalsize = c^+ = u_{crest} + \sqrt{g(h+a)} , \qquad (5) [/math]
where [math]a[/math] is the wave crest height. If we assume [math]a \lt \lt h[/math], then the velocity at the wave crest [math]u_{crest}[/math] can be derived from the linearized equations (3) (i.e., replacing [math]\partial(Du)/\partial x[/math] by [math]\partial(hu)/\partial x[/math] and neglecting the term [math]u \partial u / \partial x[/math]), with the result [math]u_{crest} = (a/h) \sqrt{gh}[/math]. Substitution in Eq. (5) yields
[math]c^+ \approx \Large\frac{a}{h}\normalsize \sqrt{gh} + \sqrt{g(h+a)} \approx \sqrt{gh} (1 + \Large\frac{3a}{2h}\normalsize) . \quad \quad (6)[/math]
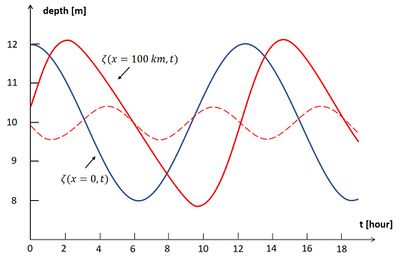
In the same way one finds for the propagation velocity of the low-water (LW) location [math]c^- \approx \sqrt{gh} (1 – \frac{3a}{2h})[/math]. Another method to find this result is presented in the appendix. As HW propagates faster than LW, the tidal wave front will steepen progressively; the duration of rising tide shortens while the duration of falling tide is lengthened. This positive tidal asymmetry increases with the relative tidal amplitude [math]a/h[/math] as a consequence of the nonlinear terms [math]\partial(\zeta u) / \partial x [/math] and [math] u \partial u / \partial x[/math] in the tidal equations. The resulting tidal distortion is illustrated in Fig. 2. Equation (6) suggests that after some time the high-water wave crest will overtake the low-water wave trough. However, this can only happen when the amplitude of the M4 overtide is of the same order of magnitude as the M2 tide, which violates the approximations used in Eq. (6).
The tidal equations for a prismatic channel do not well represent tidal propagation in estuaries because of neglect of the friction term. The equations (3) are more representative for the along-shore propagation of a tidal Kelvin wave, far away from hard boundaries where the tidal wave can reflect or from hydrodynamic boundaries where the Kelvin wave meets other tidal wave systems. An increasing tidal asymmetry develops in situations where the coastal zone is shallow and the tidal amplitude is large. The increasing tidal asymmetry along the coast of Normandy (France) can be understood in this way (Fig. 3), as well as the increasing tidal asymmetry along the North Sea coast of Holland (see: Coriolis and tidal motion in shelf seas). The tidal wave that enters estuaries situated along such coasts (the Seine at Le Havre, for instance) exhibits already significant positive-duration tidal asymmetry.
Tidal wave deformation in the presence of friction and intertidal areas
Tidal asymmetry develops during up-channel propagation into a shallow tidal basin. Pronounced tidal asymmetry (possibly leading to tidal bore formation) only occurs if during propagation a sufficiently large ratio [math]a/h[/math] is maintained. In many cases this condition is not met, because the tidal amplitude decreases during propagation. The two main reasons for decrease of the tidal amplitude are: (1) tidal wave damping by friction and (2) lateral spreading of the flood tidal wave. These two nonlinear processes also influence the propagation of the high-water wave crest and the low-water wave trough.
We consider a tidal basin where the longitudinal tidal flow [math]u(x,t)[/math] is confined in a single tidal channel with depth [math]D(x,t)[/math] and width [math]B_C(x)[/math]. Flood water can spread over intertidal areas; the width of the intertidal area [math]B_I(x,t)[/math] is a function of the water level [math]\zeta(x,t)[/math]. The tidal propagation in this basin can be described by the mass and momentum balance equations
[math]B \Large\frac{\partial \zeta}{\partial t}+\frac{\partial}{\partial x}\normalsize (B_C Du) = 0 , \qquad (7)[/math]
[math]\Large\frac{\partial u}{\partial t}\normalsize + u \Large\frac{\partial u}{\partial x} \normalsize + g \Large\frac{\partial \zeta}{\partial x}\normalsize + F = 0 , \qquad (8)[/math]
where [math]B= B_C+B_I [/math] is the total surface width. The symbol [math]F[/math] in Eq. (8) stands for the frictional momentum dissipation which is usually represented by a quadratic expression of the form [math]F= c_D \large\frac{|u|u}{D} [/math]. Although it appears from detailed measurements that this expression is a rough approximation – the friction coefficient [math]c_D[/math] is found to be variable both temporally and spatially (Lewis and Lewis, 1987[9]; Stacey and Ralston, 2005[10]; Lefebvre et al., 2012[11]) – we consider here a further approximation assuming that the quadratic dependence on [math]u[/math] can be ignored: [math]F = r \large\frac{u}{D}[/math]. The linear friction coefficient [math]r[/math] is constant with dimension [m/s]; it relates momentum dissipation at the channel bed linearly to the depth-averaged current velocity. Its value typically ranges between 0.001 - 0.004 m/s [1]. The precise value of the friction coefficient for estuarine flow is generally not well known as it is influenced by many factors such as density stratification (lower friction), small bed forms (higher friction) and fluid mud layers (lower friction). The friction coefficient may even be different for ebb and flood because of differences in salinity stratification[10]. In most estuaries, the tidal discharge amplitude is much larger than the river discharge, which therefore does not strongly influence frictional dissipation in the absence of salinity stratification. In this case, the linearization of the friction term is a minor approximation compared to the uncertainty in the value of the friction coefficient. The situation where tidal discharge and river discharge are comparable is discussed in the article River tides.
The tidal equations (7) and (8) are too complicated for an analytic treatment in which tidal asymmetry is explicitly related to the nonlinear terms. An analytical solution of the tidal equations requires further approximations, by assuming that the contribution of nonlinear terms is relatively small and can be linearized (Lanzoni and Seminara, 1998[12]).
Therefore we consider a prismatic tidal channel with a uniform mean depth [math]h[/math] much larger than the tidal amplitude [math]a[/math], such that the friction term can be approximated by
[math]F = r \Large\frac{u}{D}\normalsize =r \Large\frac{u(x,t)}{h+\zeta(x,t)}\normalsize \approx r\Large\frac{u(x,t)}{h}\normalsize (1 - \Large\frac{\zeta(x,t)}{h}\normalsize) . \qquad (9)[/math]
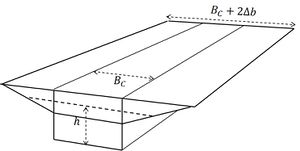
We further assume that the intertidal storage width [math]B_I[/math] is much smaller than the channel width [math]B_C[/math] and that it increases linearly with the water level [math]\zeta(x,t)[/math] (see Fig. 4):
[math]B_I = \Delta b (1 + \Large\frac{\zeta(x,t)}{h}\normalsize), \quad \lt B\gt =B_C+\Delta b . \qquad (10)[/math]
In shallow estuaries ([math]h \le 5 m[/math]) with strong tides, the nondimensional friction coefficient [math]r / (h \omega)[/math] is substantially larger than 1 (the symbol [math]\omega \equiv 2 \pi / T[/math] is the M2 tidal radial frequency). In this case the inertial terms [math]\partial u / \partial x [/math] and [math] u \partial u / \partial x[/math] are much smaller than the friction term [math]F[/math].
In prismatic well-mixed estuaries, where salinity stratification can be ignored and where frictional effects are much stronger than inertial effects, the one-dimensional cross-section-averaged tidal equations (7) and (8) for small values of [math]a/h[/math] can be simplified to
[math]\lt B\gt \Large \frac{\partial \zeta}{\partial t} \normalsize + h B_C \Large \frac{\partial u}{\partial x}\normalsize + \Delta b \Large \frac{\zeta}{a} \frac{\partial \zeta}{\partial t} \normalsize + B_C \Large \frac{\partial (\zeta u)}{\partial x}\normalsize =0 , \quad \quad (11)[/math]
[math]g\Large \frac{\partial \zeta}{\partial x}\normalsize + r \Large \frac{u}{h}\normalsize – r \Large \frac{u \zeta}{h^2}\normalsize =0 . \quad \quad (12)[/math]
In such friction-dominated estuaries the tide does not travel as a propagating wave, but rather advances into the estuary through a diffusion-type process, as shown by Eq. (A5) and described by Blondeaux (1978) for the Saint Lawrence Estuary [13]. The tidal wave crest does not coincide with the time of high water, but lags behind. The same applies to low water.
The nonlinear terms in the tidal equations are much smaller than the linear terms if [math]\Delta b \lt \lt B_C[/math] and [math]a/h \lt \lt 1[/math]. In this case a first order solution [math]\zeta^{(1)}[/math] can be found by substituting the solution of the linear equations in the nonlinear terms. The nonlinear terms then generate a small M4 tidal component [math]\zeta^{(2)}[/math], which affects the duration of tidal rise and tidal fall. This is because the propagation speed [math]c^+[/math] of the high-water wave crest differs from the propagation speed [math]c^-[/math] of the low-water wave trough (see appendix):
[math]c^{\pm} \approx [1 \pm (2 - \sqrt{2}) ( \Large\frac{2a}{h}\normalsize - \Large\frac{\Delta b}{2\lt B\gt }\normalsize )] \; \sqrt{gh} \; \sqrt{ \Large\frac{2 \omega h}{r} \frac{B_C}{\lt B\gt }\normalsize} . \quad \quad (13) [/math]
This expression exhibits the effect of other nonlinearities in tidal propagation than those considered in the example of the prismatic channel: the effect of intertidal areas in Eq. (11) and the effect of depth dependence of the friction term in Eq. (12). The nonlinearity in the friction term Eq. (9) implies less friction in the period around HW compared to the period around LW and a corresponding increase of the HW propagation speed compared to the LW propagation, yielding positive tidal asymmetry. The nonlinearity related to the width increase with rising water level represented by the third term in Eq. (11) implies a decrease of the HW propagation velocity compared to the LW propagation, yielding negative tidal asymmetry (Speer and Aubrey, 1985[14]). This is because the HW crest of the tidal wave is delayed when propagating into the estuary by diversion of flood water over the intertidal area, while the LW wave trough remains confined within the narrower channel when propagating into the estuary. Hence, shallowness of the channel (large [math]a/h[/math]) and large intertidal area (large [math]\Delta b/B_C[/math]) have counteracting effects on tidal wave distortion.
Morphology of shallow tidal basins with small river inflow
In the foregoing it was shown that the tidal wave that enters a shallow prismatic channel is distorted due to the opposite effects of friction and intertidal areas on the up-channel propagation of HW on the one hand and LW on the other. In short tidal basins, these effects are partially offset by the reflected tidal wave at the landward basin boundary[1]. However, in the case of strong friction, the reflected tidal wave is much smaller than the incoming tidal wave in a large part of the basin. In this part of the tidal basin the tidal velocity [math]u[/math] is mainly determined by the water surface slope [math]\partial \zeta /\partial x[/math], according to Eq. 12. A short period of tidal rise compared to the period of tidal fall implies steeper water surface slopes during flood than during ebb. Hence, maximum flood velocities are higher than maximum ebb velocities in the absence of significant river inflow.
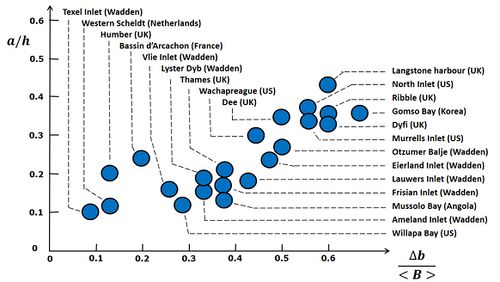
Because the transported sediment load increases more than linearly with the current velocity (according to Eq. 2), sediment fluxes during flood tide are higher than sediment fluxes during ebb tide. Flood-dominant tidal asymmetry thus produces a net import of sediment into the basin. Sediment infill could possibly go on until no tidal basin is left. This has happened in the past to some tidal basins, but many tidal basins without river inflow still survive. The reason is that flood dominance is neutralized by several processes. One of these processes is wave action, which can suspend large amounts of sediment in the HW period that are subsequently transported out of the basin by ebb currents[15][16]. However, tidal basins do not depend only on wave action for their survival. One reason is the so-called Stokes transport, the water outflow compensating for the net influx due to greater mean water depth during flood than during ebb. Another reason is the reduction of tidal asymmetry due to the presence of intertidal areas as discussed in the previous section. During the development of intertidal areas by flood-dominant sediment transport, tidal asymmetry is weakened until the average sediment transport by flood currents has become comparable to the average transport by ebb currents. In order to neutralize flood dominance with increasing relative tidal amplitude [math]a/h[/math], the counteracting effect of intertidal areas should also increase. Fig. 5 shows that this is indeed the case for natural tidal basins with small (or without) river inflow: tidal basins with larger relative tidal amplitude have larger intertidal areas. One may thus conclude that self-organizing processes can produce a natural equilibrium morphology for tidal basins in a sedimentary environment without geological constraints (see also the article Morphology of estuaries). A mathematical derivation of the relationship between [math]a/h[/math] and [math]\Delta b/\lt B\gt [/math] that should be approximately satisfied in case of a natural morphodynamic equilibrium is given in Dronkers (1998[17] and 2017[1]). This relationship depends on the tidal asymmetry already present at the tidal basin inlet and is therefore different for different tidal basins.
Tidal wave deformation in a converging channel
The influence of friction on tidal propagation increases with decreasing depth. The LW propagation is slowed down more strongly than the HW propagation, which results in a larger tidal asymmetry. However, the tidal amplitude is decreased by frictional damping. During the past century many estuaries have been deepened for navigational purposes and intertidal areas have been reclaimed. The effect of these interventions on tidal propagation is illustrated in Fig. 6 for the Seine estuary and tidal river system. The tide propagates now much faster into the estuary and the tidal amplitude is much larger, especially in the upstream river. The tide propagation speed has increased more for the low waters than for the high waters, although the propagation of the high waters also benefits of the reduction of the intertidal areas. In the past a high tidal bore developed each spring tide in the downstream Seine river. After the interventions (especially the dredging of the mouth bar) it takes a much larger distance before the HW wave crest overtakes the LW wave trough. A small tidal bore now develops far upstream and only for very high tidal coefficients[18].
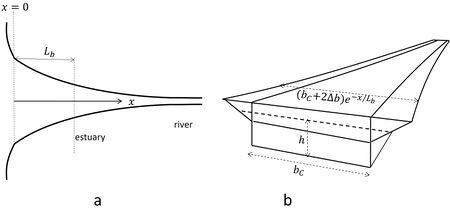
As discussed before, the expansion of the tidal flood wave over large intertidal areas decreases its height and propagation speed. The opposite occurs when the tide propagates into a tidal channel that becomes progressively narrower in up-channel direction, see Fig. 7. Instead of expanding laterally, the tidal wave is contracted when propagating. In the hypothetical case of no friction, conservation of the tidal energy flux along the channel requires up-channel amplification of the tidal amplitude (according to Green's law[20]). Many estuaries with significant river inflow have an upstream converging channel. Intertidal areas are rather small, partly as a result of natural sedimentation but often also as a result of human reclamation. The channel depth along the thalweg is fairly uniform[21], but shoals may be present in the mouth zone. The uniformity of the depth can also be due to dredging works for navigation purposes.
Insight in the role of the most important nonlinear terms can be gained when simplifications are made. In the following we consider an idealized estuary with exponentially converging width. The corresponding estuarine geometry is shown in Fig. 7. The mean water depth [math]h[/math] is uniform throughout the estuary; the channel width [math]B[/math] converges exponentially and the intertidal width [math]B_I[/math] increases linearly from the LW level up to the HW level,
[math]B_C = b_C e^{-x/L_b} , \; B_I = e^{-x/L_b} \Delta b (1 + \zeta / a), \; \lt B\gt =b e^{-x/L_b} ; \; b = b_C+\Delta b. \quad \quad (14)[/math]
It should be borne in mind that although many estuaries have an upstream converging width, the assumption of exponential width convergence and uniform depth is for most estuaries a very rough approximation. Often only a limited part of the estuary can be represented in this way.
Tidal propagation in this part of the estuary can be described by the mass and momentum balance equations (7) and (8). The instantaneous local depth is [math]D(x,t)=h+\zeta(x,t)[/math] and the cross-sectional averaged tidal velocity is [math]u(x,t)[/math]. Density gradients are left out of consideration. When substituting the expressions (14) for the width and omitting all nonlinear terms we obtain
[math] \Large \frac{b}{b_C} \frac{\partial \zeta}{\partial t}\normalsize + h \Large \frac{\partial u}{\partial x}\normalsize – u \Large \frac{h}{L_b} \normalsize = 0 . \quad \quad (15)[/math]
[math]\Large\frac{\partial u}{\partial t}\normalsize + g \Large \frac{\partial \zeta}{\partial x}\normalsize + r \Large \frac{u}{h}\normalsize = 0 . \quad \quad (16)[/math]
Solving these linear equations (only tide, no river discharge) yields
[math]\zeta = a e^{-\mu x} \; cos(kx-\omega t) \quad [/math] with [math]\quad 2 L_b \; \mu = \normalsize -1 + \Large[\normalsize 1 – (\Large \frac{1}{2} \normalsize + 2 K_0^2) +\large[\normalsize (\Large \frac{1}{2}\normalsize + 2 K_0^2 )^2+ 4 (K_c^2 - K_0^2) \large]^{\large 1/2} \Large]^{\large 1/2} \normalsize, \quad \quad (17)[/math]
where [math]K_0 = \Large \frac{\omega L_b}{\sqrt{ghb_C/b}}\normalsize , \; K_c = \Large \frac{r \omega L_b^2b}{g h^2b_C} \normalsize [/math]. The damping factor [math]\mu[/math] is positive for large friction and large convergence length ([math]K_c \gt K_0[/math]). However, for small friction and small convergence length ([math]K_c \lt K_0[/math]) the damping factor is negative: the tide is amplified when propagating up-channel. Even in the case of strong friction, the tide is only slightly damped or even amplified if the convergence length [math]L_b[/math] is sufficiently small. In cases where tidal damping dominates over the effect of channel convergence (large [math]L_b[/math]), the relative tidal amplitude decreases along the estuary; tidal asymmetry then becomes less relevant for upstream sediment transport. As noted before, the friction factor [math]r[/math] can vary greatly between estuaries because of salinity stratification and the type of bed sediments (coarse or muddy) and bedforms.
The solution of the Eqs. (15) and (16) also yields an expression for the wave propagation velocity [math]c[/math]:
[math]c = \Large \frac{\omega}{k}\normalsize = 2 \omega L_b \Large[\normalsize - 1 + (\Large \frac{1}{2} \normalsize + 2 K_0^2) +\large[\normalsize (\Large \frac{1}{2}\normalsize + 2 K_0^2 )^2+ 4 [K_c^2 - K_0^2] \large]^{\large 1/2} \Large]^{\large -1/2}\normalsize . \quad \quad (18)[/math]
The expressions (17) and (18) show that tidal wave propagation depends on only two parameters, [math] K_0[/math] and [math] K_c [/math]. It should be noted that the linear equations (15) and (16) do not describe tidal wave deformation; for this, nonlinear terms have to be included ([math]u \partial u /\partial x[/math] and time varying water depth [math]h+\zeta[/math] in Eq. (15) and [math]b \zeta \partial u / \partial x[/math] in Eq. (16)).
In strongly converging friction-dominated estuaries the nondimensional wave numbers [math] K_0[/math] and [math] K_c [/math] have similar order of magnitude (consider, for example, [math]r \approx[/math] 0.003 m/s, and the typical geometries [math]\Delta b \lt \lt b_C[/math], convergence length [math]L_b \approx[/math] 25 km and depth [math]h \approx[/math] 8 m, or convergence length [math]L_b \approx[/math] 10 km and depth [math]h \approx[/math] 5 m). In this case [math]\mu \approx 0[/math]: the longitudinal variation of the tidal amplitude is small. Although friction causes damping of the tidal amplitude along the estuary, observations show that the tidal amplitude in many estuaries is fairly uniform along the estuary (Friedrichs and Aubrey, 1994[22]; Prandle, 2004[23]; Savenije, 2012[21] ); see also the article Physical processes and morphology of synchronous estuaries. The reason is that tidal amplification by the funneling effect approximately cancels tidal damping due to friction. In a strongly, exponentially converging estuary the tide is propagating upstream with a phase difference of approximately 90° between tidal elevation and tidal velocity (Jay, 1991[20]). In some estuaries the funneling effect even produces an increase of the tidal amplitude in the strongly converging part of the estuary; examples are the Hooghly (Fig. 1), Scheldt, Humber, Gironde-Garonne.
In the case of strong friction and strong exponential width convergence, the tidal equations (7) and (8) can be simplified by neglecting the term [math]B_C \partial (Du) / \partial x[/math] compared to [math]Du \partial B_C / \partial x[/math] in Eq. (7) and the terms [math]\partial u / \partial t[/math], [math] u \partial u / \partial x[/math] compared to [math]ru/h[/math] in Eq. (8). The two simplified equations can be combined by eliminating [math]u[/math]. This yields the simple characteristic equation
[math]\Large\frac{d}{dt}\normalsize \zeta(x(t),t) = 0 , \quad \Large\frac{d x(t)}{dt}\normalsize = c = \Large\frac{g B_C D^2}{r B L_b}\normalsize . \quad \quad (19)[/math]
We assume that the relative tidal amplitude [math]a/h[/math] and the relative intertidal area [math]\Delta b / b_C[/math] are small, then according to Eq. (14),
[math]D^2 \approx h^2 (1 + 2 \Large\frac{\zeta}{h}\normalsize), \quad \Large\frac{B}{B_C}\normalsize \approx \Large\frac{b}{b_C}\normalsize (1+\Large\frac{\zeta}{a}\frac{\Delta b}{b}\normalsize ) .[/math]
The HW propagation velocity [math]c^+[/math], and LW propagation velocity [math]c^-[/math] then follow directly from Eq. (19):
[math] c^{\pm} \approx \Large\frac{g b_C h^2}{r L_b b}\normalsize \; (1 \pm \Large\frac{2a}{h}\normalsize \mp \Large\frac{\Delta b}{b}\normalsize ) . \qquad (20)[/math]
A similar expression is given by Friedrichs and Aubrey (1994) [22] from an analytical model of converging estuaries with small relative tidal amplitudes and small intertidal areas. The role of the nonlinear terms for tidal distortion is similar as for the prismatic channel. The nonlinearity in the friction term Eq. (9) implies less friction in the period around HW compared to the period around LW and a corresponding increase of the HW propagation speed compared to the LW propagation, yielding positive tidal asymmetry. The nonlinearity related to the width increase with rising water level Eq. (10) implies a decrease of the HW propagation velocity compared to the LW propagation, yielding negative tidal asymmetry.
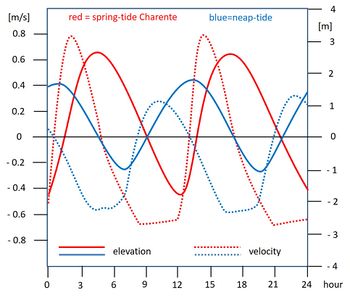
The examples of tidal propagation in a prismatic channel and tidal propagation in a strongly converging estuary show that strong positive tidal asymmetry will develop only in estuaries with a large relative tidal amplitude [math]a/h[/math] and small relative intertidal area [math]\Delta b / b_C[/math]. The analytic models can only be evaluated for small values of [math]a/h[/math]. However, the physical mechanisms for the development of strong tidal asymmetry are basically the same when [math]a/h[/math] is no longer a small quantity, as confirmed by fully nonlinear mathematical models (Peregrine, 1966[25]; Filippini, 2019[26]). The importance of the parameter [math]a/h[/math] for the development of positive tidal asymmetry is illustrated by observations that show a positive tidal asymmetry at spring tide and a negative tidal asymmetry at neap tide in the Pungue estuary (Mozambique; Nzualo et al., 2018[27]) and the Charente estuary (France; Toublanc et al., 2015[28]). This is illustrated in Fig. 8 for the Charente estuary, by comparing the curves for tidal elevation and current velocity for springtide (large [math]a/h[/math]) and neap tide (small [math]a/h[/math]). During springtide the tidal rise is much steeper than for neap tide. The maximum flood current velocity is larger than the maximum ebb tidal velocity for springtide, while the opposite holds for neap tide.
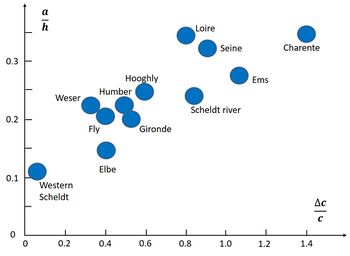
In Fig. 9 the relative difference between HW and LW propagation speeds [math]\Delta c / c = 2(c^+ -c^-)/(c^++c^-)[/math] are compared for estuaries with different relative tidal amplitude [math]a/h[/math]. The figure shows a positive correlation between [math]\Delta c / c [/math] and [math]a/h[/math]. Although [math]a/h[/math] is the most important parameter, other factors also influence the relation between [math]a/h[/math] and [math]\Delta c / c[/math], such as [math]K_0[/math] and [math]K_c[/math] (representing depth [math]h[/math], convergence length [math]L_b[/math] and friction parameter [math]r[/math]), the relative intertidal area [math]\Delta b/b_C[/math] and the mean river discharge [math]Q_R[/math]. The dependence of [math]\Delta c / c [/math] on [math]a/h[/math] is therefore different for each estuary.
Equation (20) yields an estimate for the location [math]x[/math] where the high-water wave crest overtakes the low-water wave trough, assuming that the tide at the estuarine mouth ([math]x=0[/math]) is approximately symmetric and assuming that Eq. (20) remains approximately valid in the strong nonlinear case. For an estuary with small intertidal areas the distance [math]x[/math] is given by
[math]x = \Large\frac{\pi}{4}\frac{gh^2}{\omega r L_b}\frac{h}{a}\normalsize . \quad \quad (21)[/math]
For example, in the case of the Gironde-Garonne estuary and tidal river system ([math]a \approx 2.5 m, h \approx 8 m, L_b \approx 35 km, r \approx 0.0025 m/s[/math]) we find [math]x \approx 130 [/math] km from the estuarine mouth, which is close to the location where a tidal bore is often observed. This example shows that a tidal bore will form if (1) frictional damping of the tidal wave is compensated by the funneling effect of width convergence and (2) the distance over which the tide can propagate into the estuary is sufficiently long (see also the article Tidal bore dynamics).
In estuaries where frictional damping is not compensated by the funneling effect of width convergence, tidal asymmetry is generated in a similar way by the nonlinear processes described above (Friedrichs and Madsen, 1992[29]). However, reduction of the relative tidal amplitude [math]a/h[/math] by damping of the tidal wave may prevent tidal bore development.
Morphology of estuaries with tidal rivers
In a converging (funnel-shaped) estuary with strong friction, the tidal velocity [math]u[/math] is mainly determined by the water surface slope [math]\partial \zeta /\partial x[/math], according to Eq. 12. A short period of tidal rise compared to the period of tidal fall implies steeper water surface slopes during flood than during ebb, with maximum flow rates that are higher during flood than during ebb, as illustrated in Fig. 8. Therefore, sediment fluxes during flood tide are higher than sediment fluxes during ebb tide, resulting in a net import of sediment into the estuary. As shown before, flood dominance increases with increasing relative tidal amplitude [math]a/h[/math]. Tidal asymmetry develops as the tidal wave propagates in the estuary. The time it takes for the tidal wave to propagate through the convergent part of the estuary, [math]L_b/c[/math], is therefore another factor that determines the degree of tidal asymmetry. A corresponding nondimensional quantity that is indicative of the time duration for tidal asymmetry development is given by [math]L_b \omega/ c[/math]. It can thus be expected that the strength of flood dominance is positively correlated with the nondimensional parameter [math]a L_b \omega / (h c)[/math].
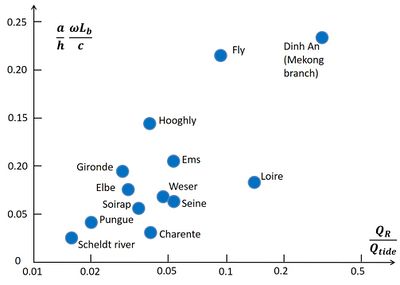
Infill of estuaries is limited by sediment export through river flow, although dredging may also play a role. The influence of river flow on sediment export can be represented by the nondimensional parameter [math]Q_R/Q_{tide}[/math], where [math]Q_R[/math] is the mean river discharge and [math]Q_{tide}[/math] the maximum tidal discharge in the mid-estuarine zone ([math]x \approx L_b/2[/math]). For estuaries in morphological equilibrium, sediment import due to tidal asymmetry (flood dominance) should be approximately balanced by export due to river flow. Comparing different estuaries one may thus expect a positive correlation between the parameters [math]a L_b \omega / (h c)[/math] and [math]Q_R/Q_{tide}[/math]. As shown in Fig. 10, such a positive correlation exists, although the spread in the data is large. This spread can be due to many other factors, which influence sediment import and export in different ways. Possible important factors are[1]:
- nonequilibrium morphology, due to dredging and other engineering interventions,
- import/export by wave activity,
- import by estuarine circulation,
- sediment recirculation in ebb/flood-channel cells,
- sediment import/export related to settling and erosion time lags,
- fluvial sediment supply,
- influence of intertidal areas on tidal asymmetry,
- type of sediment.
A mathematical derivation of the relation between [math]L_b \omega/ c[/math] and [math]Q_R/Q_{tide}[/math] is given in Dronkers (2017[30]).
Symbols
| Variable | Description | Variable | Description | Variable | Description |
|---|---|---|---|---|---|
| [math]a[/math] | tidal amplitude | [math]D[/math] | total depth | [math]q_s[/math] | sediment transport |
| [math]b[/math] | tide-mean width at the inlet ([math]x=0[/math]) | [math]F[/math] | friction term | [math]r[/math] | coefficient linear friction |
| [math]\Delta b[/math] | tide-mean with intertidal zone at the inlet | [math]g[/math] | gravitational acceleration | [math]t[/math] | time |
| [math]b_C[/math] | tidal channel width at the inlet ([math]x=0[/math]) | [math]h[/math] | tide-mean depth | [math]T[/math] | semidiurnal tidal period |
| [math]B[/math] | total estuary width | [math]HW[/math] | high water | [math]x[/math] | longitudinal coordinate |
| [math]B_C[/math] | tidal channel width | [math]K_0[/math] | dimensionless wavenumber | [math]\gamma[/math] | skewness coefficient |
| [math]B_I[/math] | width intertidal zone | [math]K_c[/math] | dimensionless damping number | [math]\zeta[/math] | tide elevation |
| [math]c[/math] | tidal wave celerity | [math]L[/math] | tidal wavelength | [math]\mu[/math] | damping coefficient |
| [math]\Delta c[/math] | difference HW - LW propagation speeds | [math]L_b[/math] | estuary convergence length | [math]\omega[/math] | semidiurnal radial frequency |
| [math]c_D[/math] | friction coefficient | [math]LW[/math] | low water | [math] \lt …\gt [/math] | tide averaged value |
Related articles
- Morphology of estuaries
- Ocean and shelf tides
- Tidal bore dynamics
- Tidal motion in shelf seas
- Estuarine circulation
- Estuarine turbidity maximum
- River tides
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Dronkers, J. 2017. Dynamics of Coastal Systems. World Scientific Publ. Co, Singapore, 740 pp.
- ↑ Nidzieko, J. 2010. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides. J. Geophysical Research 115, C08006, doi:10.1029/2009JC005864
- ↑ Doodson, A.T. 1921. The harmonic development of the tide-generating potential. Proc.R.Soc.London, Ser.A 100: 305-329
- ↑ Hoitink, A.F.J., Hoekstra, P. and van Mare, D.S. 2003. Flow asymmetry associated with astronomical tides: Implications for residual transport of sediment. J.Geophys.Res. 108: 13-1 - 13-8
- ↑ Zhang, W., Cao, Y., Zhu, Y., Zheng, J., Ji, X., Xu, Y., Wu, Y. and Hoitink, A.F.J. 2018. Unravelling the causes of tidal asymmetry in deltas. Journal of Hydrology 564: 588–604
- ↑ Song, D., X. H. Wang, A. E. Kiss, and Bao, X. 2011. The contribution to tidal asymmetry by different combinations of tidal constituents. J. Geophys. Res., 116, C12007
- ↑ TPXO ATLAS Global and Regional Solutions
- ↑ Banerjee, A.P., Dutta, S. and Majumdar, A. 2015. Quest for the determination of environmental flow assessment for hilsa fish of the Hooghly estuary by hydraulic rating method. ARPN Journal of Engineering and Applied Sciences 10: 7885-7899
- ↑ Lewis, R. E., and Lewis, J. O. 1987. Shear-stress variations in an estuary. Estuarine Coastal Shelf Sci. 25: 621–635
- ↑ 10.0 10.1 Stacey, M.T. and Ralston, D.K. 2005. The Scaling and Structure of the Estuarine Bottom Boundary Layer. J. Physical Oceanography 35: 55-71
- ↑ Lefebvre, A., Ernstsen, V.B and Winter, C. 2012. Estimation of roughness lengths and flow separation over compound bedforms in a natural-tidal inlet. Continental Shelf Research 61–62: 98-111
- ↑ Lanzoni, S. and Seminara, G. 1998. On tide propagation in convergent estuaries, J. Geophys. Res. 103: 30793–30812
- ↑ LeBlond, P. 1978. On tidal propagation in shallow rivers, J. Geophys. Res., 83: 4717–4721
- ↑ Speer, P.E. and Aubrey, D.G. 1985. A study of non-linear tidal propagation in shallow inlet/estuarine systems. Part II: theory. Estuarine, Coastal Shelf Sci. 21: 207-224
- ↑ Friedrichs, C.T. 2011. Tidal Flat Morphodynamics: A Synthesis. In: Treatise on Estuarine and Coastal Science, vol. 3, Estuarine and Coastal Geology and Geomorphology. Ed.:J. D. Hansom and B. W. Fleming, Elsevier, Amsterdam: 137-170
- ↑ Desguée, R., Robin, N., Gluard, L., Monfort, O., Anthony, E.J., Levoy, F. 2011. Contribution of hydrodynamic conditions during shallow water stages to the sediment balance on a tidal flat: Mont-Saint-Michel bay, Normandy, France. Estuarine Coastal Shelf Sci. 94: 343–354
- ↑ Dronkers, J. 1998. Morphodynamics of the Dutch Delta. In: Physics of estuaries and coastal seas. Ed.: J.Dronkers and M.B.A.M. Scheffers, Balkema, Rotterdam: 297-304
- ↑ Bonneton, N., Bonneton, P., Parisot, J-P., Sottolichio, A. and Detandt G. 2012. Tidal bore and Mascaret - example of Garonne and Seine Rivers. Comptes Rendus Geosciences, 344, 508-515
- ↑ Comoy, M. 1881. Etude pratique sur les marées fluviales. Gauthiers-Villars, Paris
- ↑ 20.0 20.1 Jay, D.A. 1991. Green's law revisited: tidal long-wave propagation in channels with strong topography. J.Geophys.Res. 96: 20,585-20,598
- ↑ 21.0 21.1 Savenije, H.H.G. 2012. Salinity and Tides in Alluvial Estuaries, second ed., Salinity and Tides in Alluvial Estuaries, second ed., www.salinityandtides.com
- ↑ 22.0 22.1 Friedrichs C.T. and Aubrey, D.G. 1994. Tidal propagation in strongly convergent channels. J.Geophys.Res. 99: 3321-3336
- ↑ Prandle, D. 2004. How tides and river flows determine estuarine bathymetries. Progress in Oceanography 61: 1–26
- ↑ Toublanc, F., Brenon, I., Coulombier, T. and LeMoine, O. 2015. Fortnightly tidal asymmetry inversions and perspectives on sediment dynamics in a macrotidal estuary (Charente, France). Continental Shelf Res. 94: 42–54
- ↑ Peregrine, D.H. 1966. Calculations of the development of an undular bore J. Fluid Mech. 25: 321–30
- ↑ Filippini, A.G., Arpaia, L., Bonneton, P. and Ricchiuto, M. 2019. Modeling analysis of tidal bore formation in convergent estuaries. European Journal of Mechanics - B/Fluids 73: 55-68
- ↑ Nzualo, T.N.M., Gallo, M.N. and Vinzon, S.B. 2018. Short-term tidal asymmetry inversion in a macrotidal estuary (Beira, Mozambique). Geomorphology 308: 107–117
- ↑ Toublanc, F., Brenon, I., Coulombier, T. and LeMoine, O. 2015. Fortnightly tidal asymmetry inversions and perspectives on sediment dynamics in a macrotidal estuary (Charente,France). Continental Shelf Res. 94: 42–54
- ↑ Friedrichs, C.T. and Madsen, O.S. 1992. Non-linear diffusion of the tidal signal in frictionally dominated embayments. J.Geophys.Res. 97: 5637-5650
- ↑ 30.0 30.1 Dronkers, J. 2017. Convergence of estuarine channels. Continental Shelf Res. 144: 120–133
Appendix
The solution of the first order linear equations (3) is
[math]\zeta^{(1)}=a \cos \theta , \; u^{(1)} = \Large\frac{c_0}{h}\normalsize \zeta^{(1)} , \quad \quad (A1)[/math]
where [math]\theta= k_0 x-\omega t[/math], [math]\omega[/math] is the M2 radial frequency, the wave number [math]k_0 = \Large \frac{\omega}{gh} \normalsize[/math] and [math]c_0=\omega / k[/math].
After substitution in the nonlinear terms we have a linear equation for the second order approximation. The solution is
[math]\zeta = \zeta^{(1)} + \zeta^{(2)} , \quad \zeta^{(2)} = \Large \frac{3 a^2}{4h}\normalsize kx \sin 2 \theta . \quad \quad (A2)[/math]
The location of the wave crest at time [math]t[/math] is called [math]x^+(t) [/math]. At this location the [math]\zeta[/math] is maximum.
[math] \Large \frac{\partial \zeta}{\partial t}\normalsize (x^+(t),t) = -a k_0 \sin \theta^+ + \Large \frac{3 a^2}{4h}\normalsize k_0 [ \sin 2 \theta^+ + 2kx \cos 2 \theta^+ ] = 0 \quad [/math] , with [math]\theta^+=k_0 x^+(t) - \omega t . \quad \quad (A3)[/math]
Because [math]a/h[/math] is small, the wave crest is at a location where [math]\theta^+[/math] is small ([math]|\theta^+ |\lt \lt 1[/math]). An approximate expression for the location of the wave crest is then given by
[math]x^+(t) \approx (1 - \Large \frac{3a}{2h}\normalsize)^{-1} c_0 t . \quad \quad (A4)[/math].
The propagation speed of the HW wave crest (Eq. A4) follows from [math]c^+(t)=dx^+/dt[/math].
The first order linear equations (9) and (10) can be solved by eliminating [math]u(x,t)[/math], yielding a diffusion equation for the tidal elevation [math]\zeta(x,t)[/math]:
[math]\Large\frac{\partial \zeta^{(1)} }{\partial t}\normalsize = \Large\frac{h^2}{r}\frac{B_C}{\lt B\gt }\frac{\partial^2 \zeta^{(1)} }{\partial x^2}\normalsize .\quad \quad (A5)[/math]
The first order solution is
[math]\zeta^{(1)} = \Large\frac{1}{2}\normalsize a e^{i (\kappa x - \omega t)} + c.c. [/math], where [math]c.c. [/math] is the complex conjugate, [math]\kappa = k+i \mu , \; k = \mu = \sqrt { \Large \frac{\omega r \lt B\gt }{2 g h^2 B_C}\normalsize }. \quad \quad (A6) [/math]
After substitution in the nonlinear terms the second order linear equations can be solved, yielding
[math]\zeta = \zeta^{(1)} + \zeta^{(2)} , \quad \zeta^{(2)} \approx \Large\frac{a}{2}\normalsize (\Large \frac{\Delta b}{4\lt B\gt } - \frac{a}{h}\normalsize) e^{-2i \omega t} (e^{2i \kappa x} -e^{\sqrt{2} i \kappa x} ) + \Large \frac{a^2}{4h}\normalsize (1 – e^{-2 \mu x}) + c.c. \quad \quad (A7)[/math]
In the same way as before the location of the wave crest is derived from the condition
[math] \Large \frac{\partial \zeta}{\partial t} \normalsize (x^+(t),t) =0[/math] for [math]| k x^+ - \omega t|\lt \lt 1[/math].
The propagation speed of the HW wave crest (Eq. 13) follows from [math]c^+(t)=dx^+/dt[/math]; this expression holds for the lower portion of the estuary where [math]kx\lt \lt 1[/math].
Please note that others may also have edited the contents of this article.
|