Tidal bore dynamics
Contents
Introduction
A tidal bore is a sudden elevation of the water surface that travels upstream an estuary with the incoming flood tide. This article describes the processes involved in this ultimate stage of tidal wave deformation and the modelling of these processes. For an introduction to the topic of tidal wave deformation the reader is referred to the article Tidal asymmetry and tidal inlet morphodynamics.

| Estuary/river name | Maximum tidal range [m] | Tide gauge location | Country |
|---|---|---|---|
| Shannon River | 5.6 | Shannon | Ireland |
| Humber,Trent | 8.3 | Hull | UK |
| Great Ouse | 7.4 | King's Lynn | |
| Severn | 12 | Portishead | |
| Dee | 9.8 | Flint | |
| Mersey | 10 | Liverpool | |
| Ribble | 10.2 | Lytham | |
| Morecambe bay, River Kent | 10.9 | Morecambe | |
| River Eden, Nith River | 10.3 | Silloth | |
| Seine | 8.5 | Honfleur | France |
| Canal de Carentan | 7 | Carentan | |
| Baie du Mont Saint Michel – Sélune River | 14 | Granville | |
| Garonne, Dordogne | 6.3 | Podensac | |
| Pungue | 7 | Beira | Mozambique |
| Qiantang | 5 | Ganpu | China |
| Indus | 4 | Port Muhammad Bin Qasim | Pakistan |
| Hooghly | 5.7 | Sagar Island | India |
| Brahmaputra | 5.7 | Chittagong | Bangladesh |
| Sittaung | 6.3 | Moulmein | Myanmar |
| Batang Lupar River | 5.6 | Kuching | Sarawak |
| Kampar River | 5.3 | Pulo Muda | Sumatra |
| Hooghly | 5.7 | Sagar Island | India |
| Fly , Bamu, Turamu , Mappi Rivers | 4.2 | estuary | West Papua |
| Styx | 6.4 | Mackay, Queensland | Australia |
| Daly River | 7.9 | estuary | |
| Turnagain Arm, Knick Arm | 7.9 | Anchorage | Alaska |
| Bay of Fundy, Petitcodiac and Salmon rivers | 16 | Truro | Canada |
| Colorado River | 7.7 | San Filipe | Mexico |
| Amazon, Araguira, Guama, Capim and Mearim Rivers | 3.4 | Macapa | Brazil |
Occurrence of tidal bores
When a tidal wave propagates upstream into an estuary, its shape is progressively distorted. In many estuaries the high-water (HW) tidal wave crest propagates faster up-estuary than the low-water (LW) tidal wave trough. HW propagates considerably faster than LW if the mean channel depth [math]D_0[/math] is not much greater than the spring tidal range [math]2a[/math] (same order of magnitude or a few times larger) and if the intertidal area is not much greater than the tidal channel surface area. The tidal rise period is shortened and the tidal wave becomes steeper during propagation. If the tidal wave can propagate sufficiently far upstream the river without strong damping, the tidal wave front may become so steep that a water level jump – a so-called tidal bore - can form at the beginning of the rising tide.
Table 1 presents estuaries and tidal rivers in which significant tidal bores have been observed (a more complete overview can be found in Bartsch-Winkler and Lynch (1988) [2] and a recently updated catalog by Colas (2017)[3]). It appears that tidal bores generally occur for large tidal ranges ([math]Tr_0[/math]) at the estuary mouth. However, such a simple criterion is not sufficient to classify estuaries in terms of tidal bore occurrence. For instance, Furgerot (2014) [4] showed that in the Sée/Mont Saint Michel estuary, [math]Tr_0[/math] must be larger than 10 m for tidal bore formation in the Sée River and, on the other hand, Bonneton et al. (2015)[5] observed tidal bores in the Gironde/Garonne estuary even for [math]Tr_0[/math] smaller than 2 m.
The estuarine shape (depth and width profiles) plays an important role in tidal bore formation. This is illustrated by the observation that regulation works (dredging, reclamation, weirs) during the past century have weakened or even completely suppressed tidal bores in many rivers, for example in the rivers Seine, Charente, Colorado and Petitcodiac. We will discuss in the following general conditions for bore formation in terms of estuary geometry and flow conditions.
Illustrations of tidal bores are shown in Fig. 1.
Tidal bore formation in funnel-shaped estuaries
The analysis of nonlinear tidal wave transformation in estuaries, in terms of tidal forcing at the estuary mouth and large-scale geometrical properties of the channel, has received considerable attention (see Tidal asymmetry and tidal inlet morphodynamics). By contrast, the extreme nonlinear tidal-wave case where tidal bores form is much less studied.
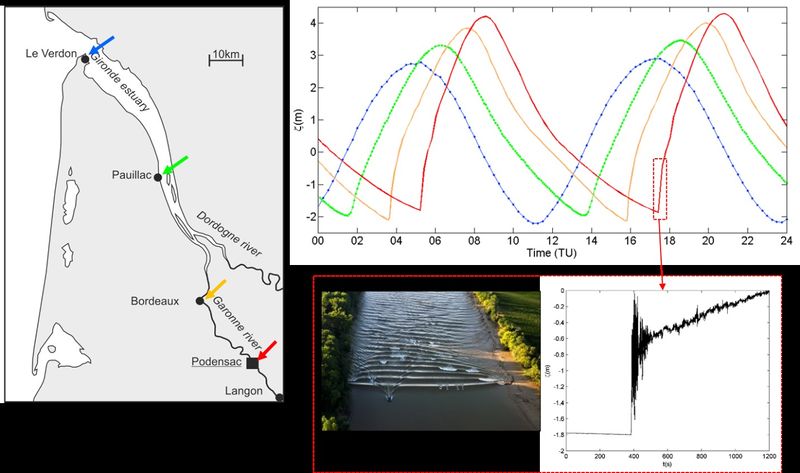
The most intense tidal bores occur in long and shallow tide-dominated funnel-shaped estuaries (e.g. Qiantang, Severn, Kampar, Gironde/Garonne/Dordogne, …) . The formation of these tidal bores is governed by the progressive distortion of the tidal wave as it propagates up the estuary. If the ebb-flood asymmetry (duration of falling tide longer than rising tide and larger flood than ebb currents) is strong enough, a tidal bore can form in the upper estuary. This is illustrated by the tidal asymmetry in the Garonne at Bordeaux (Fig. 2) and the upstream tidal bore at Podensac (Fig.3).
This extreme nonlinear deformation of a tidal wave occurs in a limited number of estuaries. To determine the conditions favourable to tidal bore occurrence, a scaling analysis can be carried out for a schematic channel geometry. A usual schematization is based on the approximations [6][7][8]:
- Uniform channel depth [math]D[/math],
- Exponential convergence of the width [math]B(x)[/math].
The convergence length [math]L_b [/math], defined as [math]L_b=B(x)/dB/dx[/math], is assumed independent of the along-channel coordinate [math]x[/math]. The forcing tidal wave at the estuary mouth can be characterized by its tidal frequency [math]\omega=2 \pi / T[/math] and its amplitude [math]A_0=Tr_0/2[/math], where [math]Tr_0[/math] is the estuary mouth tidal range. Another important parameter which influences tidal propagation in an estuary is the dimensionless mean friction coefficient [math]c_D[/math]. The tidal wave dynamics is then controlled, if we neglect fresh water discharge effects, by three dimensionless parameters:
- the nonlinearity parameter, [math]\epsilon=A_0/D[/math],
- the friction parameter, [math]\phi=c_D \sqrt{gD}/(\omega D)[/math],
- the convergence ratio, [math]\delta=\sqrt{gD}/(\omega L_b)[/math].
The formation of tidal bores is mainly governed by the progressive distortion of the tidal wave as it propagates up the estuary. This extreme nonlinear deformation of the tidal wave occurs under special conditions, in particular[5] [10]:
- a large tidal amplitude [math]a[/math],
- a long, shallow and convergent channel.
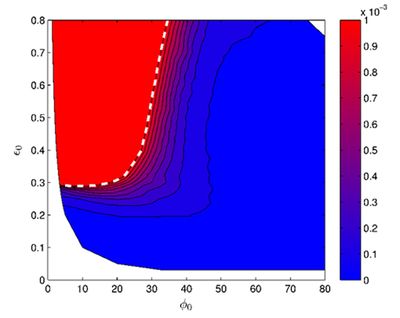
Available field data suggest that tidal bores form in convergent estuaries characterized by large values of the convergence ratio [math]\delta[/math]. Bonneton et al. (2016)[11] and Filippini et al. (2018)[9] have analysed tidal bore occurrence as a function of the dimensionless parameters [math]\epsilon[/math] and [math]\phi[/math] for a fixed value of the convergence ratio [math]\delta=2.4[/math]. Fig. 4 presents the position of convergent estuaries in the parameter space ([math]\epsilon, \phi[/math]). We can observe a clear separation between tidal-bore estuaries and non tidal-bore estuaries. Tidal bores occur when the nonlinearity parameter [math]\epsilon[/math] is greater than a critical value, [math]\epsilon_c[/math], which is an increasing function of the friction parameter [math]\phi[/math]. For small [math]\phi[/math]-values (friction parameter [math]\phi \approx 15[/math]), tidal bores can form for [math]\epsilon[/math] greater than 0.2. By contrast, for large [math]\phi[/math]-values the tidal bore formation requires much larger nonlinearity parameters. These results show that bore formation is mainly controlled by the competition between two physical processes: (a) the nonlinear distortion of the tidal wave, which is favourable to bore inception; (b) the friction dissipation of the tidal wave, which is unfavourable to bore formation.
Conditions for tidal bore formation
More generally, the analysis of tidal bores observed in natural estuaries suggests the following conditions for tidal bore formation.
The first requirement for tidal bore formation is sufficient length of the estuarine-tidal river system, i.e. the tide can penetrate far enough into the system. This depends primarily on the average longitudinal slope of the estuary-tidal river system, with a secondary role for the convergence length [math]L_b[/math]. A steep slope limits the penetration of the tide. A small channel slope is generally indicative of low-to-moderate current velocities and friction (steep slopes are generally related to strong friction generated by high current velocities and coarse bed sediments). If the longitudinal channel slope is small, the tidal bore can travel over a long distance without much dissipation.
The tidal bore develops in a section of the estuary-tidal river system where the nonlinearity parameter [math]\epsilon[/math] is large (shallow depth, large tidal range) and where the tidal wave is flood-dominant. Sometimes a tidal bore already forms close to the mouth of the estuary. This is the case with estuaries that have a large mouth bar, such as the Qiangtang estuary[12] and the Charente estuary (the latter before large-scale interventions took place). But this is rather the exception. Most often the tidal bore is formed in a section of the estuary-tidal river system further upstream, in the tidal river or on the tidal flats at the head of the estuary (as for the Garonne, Seine, Sée, etc.).
The condition of a large tidal range and a strong tidal asymmetry depends on friction; one should therefore distinguish between muddy and sandy/gravelly estuaries. If the solid fluvial flow is important with a large fraction of cohesive mud (mainly estuaries in the (sub) tropic regions, but also the Garonne) the estuarine channel bed is smooth so that the friction is weak (small [math]\phi[/math]); the tidal wave is not strongly damped. In this case a small relative channel depth (large [math]\epsilon[/math]) is the main condition to obtain a strong asymmetry of the tidal wave. Rivers with low solid discharge or supplying sandy/coarse sediments have a sandy or gravelly channel bed in the estuarine zone that produces strong friction (large [math]\phi[/math]) and strong tidal energy dissipation. In this case, strong convergence of the width of the estuary (large [math]\delta[/math]) is required to generate a large, highly asymmetric tidal amplitude (large [math]\epsilon[/math]).
River flow also influences tidal bore formation. River flow contributes to tidal wave deformation by enhancing the longitudinal velocity gradient. However, river flow also contributes to tidal wave damping and thus opposes tidal bore formation [13], see River tides. The latter effect usually dominates. Observations show that the tidal bore in the Garonne and Dordogne (France) is suppressed at high river runoff[11]. For large discharge (order of 1000 m3/s), tidal bores do not form. By contrast, for low discharge (order of 150 m3/s) a tidal bore almost always occurs in the Garonne River, even at neap tide. These findings were confirmed by Filippini et al. (2019)[9] from numerical simulations. A similar effect is observed in the Daly estuary by Wolanski et al. (2004)[14], who relate the occurrence of the tidal bore at low river discharge to the small water depth during such conditions. However, the opposite effect is reported for the Guamá-Capim river system near the mouth of the Amazon River, where tidal bores are observed only at high river discharges, in conjunction with high equinoctial tides[9].
Variations in local river geometry and water depth can also significantly affect tidal bore dynamics (Bonneton et al. (2011)[1] and Keevil et al. (2015)[15]). Observations show that tidal bores often develop in shallow rivers that discharge from the higher upstream zone into a broad estuary. If the tidal wave has already acquired sufficient asymmetry when travelling through the estuary, a tidal bore develops when the tidal wave surges into the shallow river. The presence of a mouth bar (large [math]\epsilon[/math]) is favourable to the development of strong asymmetry of the tidal wave and tidal bore formation, see Fig. 5. On the contrary, the presence of local channel width constrictions (large [math]\phi[/math]) is unfavourable to tidal bore formation, as illustrated by the absence of a tidal bore in the Conway estuary in spite of a high non-linearity parameter.

Tidal bore characteristics
A tidal bore can be schematically represented by a propagating transition between two streams of water depth [math]D_1[/math] and [math]D_2[/math], with [math]D_1 \lt D_2[/math] (see Fig. 6). Once such a hydraulic jump has developed, its flow velocities ahead and behind the jump can be derived from the mass and momentum balance equations (Fig. 6):
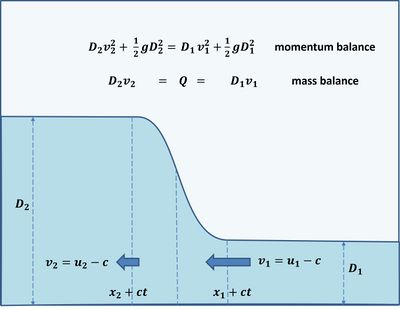
[math]v_1=u_1 – c = - \Large \sqrt{ \frac{g D_2 (D_2 + D_1)}{2 D_1}} \normalsize , \qquad (1) [/math]
[math]v_2=u_2 – c = - \Large \sqrt{ \frac{g D_1 (D_2 + D_1)}{2 D_2}} \normalsize , \qquad (2) [/math]
where [math]c[/math] is the bore celerity, [math]v[/math] the velocity in the moving frame and [math]u[/math] in the fixed frame. These equations show that the problem is entirely determined by the depth ratio [math]D_2 / D_1[/math], or equivalently by [math]\Delta D / D_1[/math], where [math]\Delta D = D_2 – D_1[/math] is the bore height. The Froude numbers around the jump, in the moving frame can be obtained from equations (1) and (2):
[math]F_1^2 = \Large \frac{v_1^2}{g D_1}\normalsize = \large \frac{D_2 (D_1+D_2)}{2 D_1^2} \normalsize , \qquad (3) [/math]
[math]F_2^2 = \Large \frac{v_2^2}{g D_2}\normalsize = \large \frac{D_1 (D_2+D_1)}{2 D_2^2} \normalsize . \qquad (4)[/math]
Knowing that [math]D_2 \gt D_1[/math], it is straightforward to see that [math]F_1 \gt 1[/math] and [math]F_2 \lt 1[/math]. The jump correspond to the passage from a supercritical flow ([math]F_1 \gt 1[/math]) to a subcritical flow ([math]F_2 \lt 1[/math]). The bore intensity is characterized equally by [math]\Delta D / D_1[/math] or by the Froude number [math]F_1[/math].
If [math]F_2 = 1[/math] (the bore height [math] \Delta D[/math] is zero) the bore velocity [math] c [/math] is equal to
[math]c_2 = u_2 + \sqrt{g D_2}[/math].
The inequality [math]F_2 \lt 1[/math] therefore implies [math]c \lt c_2[/math]. Because [math]c_2[/math] is the propagation speed of long-wave disturbances upstream of the bore, these disturbances (undulations) will catch up to the bore. A slowly propagating bore ([math]F_2 \lt \lt 1[/math]) will thus grow faster and become higher than a fast propagating bore ([math]F_1, F_2 [/math] close to 1) [16].
It can be shown that conservation of mass and momentum at the transition does not imply conservation of energy. From the mass and momentum equations the following expression for the energy dissipation is obtained [17] [18]:
[math]Q \Delta E = D_1 v_1 [ \rho g \Delta D + 0.5 \rho (v_2^2 -v_1^2) ] = \Large \frac{\rho g}{4} \sqrt{\frac{g (D_1+D_2)}{2 D_1 D_2}}\normalsize (D_2 – D_1)^3 = - \Large \frac{\rho g}{4} \frac{v_2}{D_1}\normalsize (D_2 – D_1)^3, \qquad (5)[/math]
Two forms of energy dissipation can occur at the transition, leading to two different types of bores: undular and turbulent bores.
Undular bores
For [math]F_1[/math] smaller than approximately 1.3, the bore transition is smooth and followed by a wave train (Fig. 1 right). The bore then consists of a mean jump between two water depths (see Fig. 6) on which secondary waves (amplitude [math]a[/math]) are superimposed. This type of bore is usually called an undular bore[19] and Favre (1935) [20] was the first to describe this phenomenon from laboratory experiments. That is why undular bores are sometimes referred to as Favre waves. This phenomenon, which is also named “dispersive shock” in the mathematical community, is a dispersive wave process (wave celerity depending on wavelength).
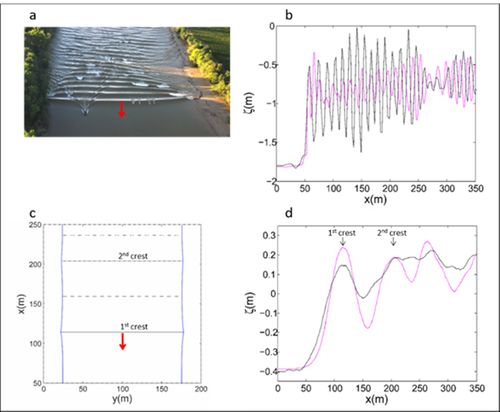
In the following we consider the case of small undular bores, [math]D_2-D_1 \lt \lt D_2[/math] and thus [math]F_1-1 \approx \Large\frac{3 (D_2-D_1)}{4 D_2}\normalsize \lt \lt 1[/math].
A simple model describing the secondary waves attached to the bore was proposed by Lemoine (1948) [17]. He considered that secondary bore waves can be approximately described by linear theory. The wave propagation speed [math]c_w[/math] in the fixed frame can be obtained from linear shallow-water wave theory,
[math](c_w - u_2)^2 = (\Large\frac{\omega}{k}\normalsize)^2 = (\Large\frac{g}{\omega}\normalsize \tanh(k D_2))^2 \approx gD_2 (1- \Large\frac{k^2 D_2^2}{3}\normalsize) , \qquad (6)[/math]
where [math]k=2 \pi / \lambda[/math] is the wave number and [math]\lambda[/math] the wavelength and [math]\Large\frac{k^2 D_2^2}{3}\normalsize \lt \lt 1[/math].
The secondary waves are stationary in a frame moving with the bore front, i.e. [math]c_w – u_2 = - v_2[/math]. By substituting this equality in Eq. (6), an estimate of the wavelength can be derived (assuming [math]D_2-D_1 \lt \lt D_2[/math]):
[math]\lambda=\sqrt{\frac{2}{3}} \pi D_2 (F_1 – 1)^{-1/2} . \qquad (7)[/math]
The bore wave energy propagates with the group velocity
[math]w_g = nc , \quad n = \frac{1}{2}+\Large\frac{k D_2}{\sinh(2 k D_2)} \normalsize \approx 3-2F_1 . \qquad (8)[/math].
The secondary bore waves are stationary in the frame moving with the bore front. In this frame the radiated wave energy flux [math]\Phi[/math] is given by
[math]\Phi = ½ g \rho (nc-c) a^2 \approx g \rho (F_1 -1) v_2 a^2 ,\qquad (9)[/math]
where [math]c \approx v_2 [/math] has been assumed.

Lemoine (1948[17]) assumed that for small undular bores, the energy dissipated at the hydraulic jump (Eq. 5) serves to maintain the secondary bore waves. The energy flux radiated by the secondary bore wave should therefore match the energy dissipation at the hydraulic jump, [math]\Phi + Q \Delta E =0[/math]. From this assumption the secondary wave amplitude can be derived as a function of [math]F_1[/math]:
[math]a=\frac{4}{3\sqrt{3}} D_2 (F_1 – 1) . \qquad (10)[/math]
Although the derivation is valid only for very small bores ([math]D_2-D_1 \lt \lt D_2[/math]), it nevertheless appears that equations (7) and (10) give a correct order-of-magnitude estimate of the observed wavelength and amplitude of undular bore propagating in rectangular channels [22][23].
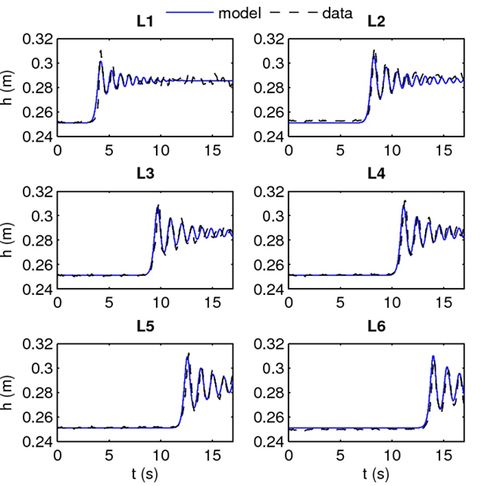
In reality, natural estuary and river channels are non-rectangular and present most of the time a variable cross-section with an approximately trapezoidal shape and gently sloping banks. The propagation of undular bores over channels with variable cross-sections was studied by Treske (1994)[24] in the laboratory and by Bonneton et al. (2015)[5] in the field. Both studies identified a transition around [math] F_t=1.15[/math]. For [math]F_1 \gt F_t[/math] the secondary wave field in the mid channel is very similar to the dispersive waves (Favre waves) described above, and follow the relations (7) and (8)[5]. For [math]F_1 \lt F_t[/math], the secondary wave wavelength in the whole channel is at least two to three times larger than in a rectangular channel for the same Froude numbers. It was shown that this new undular bore regime (Figs. 7 c,d and 8 b) differs significantly from classical dispersive undular bores in rectangular channels (i.e. Favre waves). Chassagne et al. (2019) [21] recently showed that this undular bore regime (named dispersive-like bore) is controlled by hydrostatic non-dispersive wave properties, with a dynamics similar to edge-waves in the near-shore. The transition between dispersive and dispersive-like bores is illustrated on Fig. 7 and 8. The dispersive-like bores are characterized by low wave steepness, which make them difficult to visually observe in the field. This is why such tidal bores are generally ignored and why tidal bore occurrence in the field is generally underestimated [25] [26].
Breaking bores
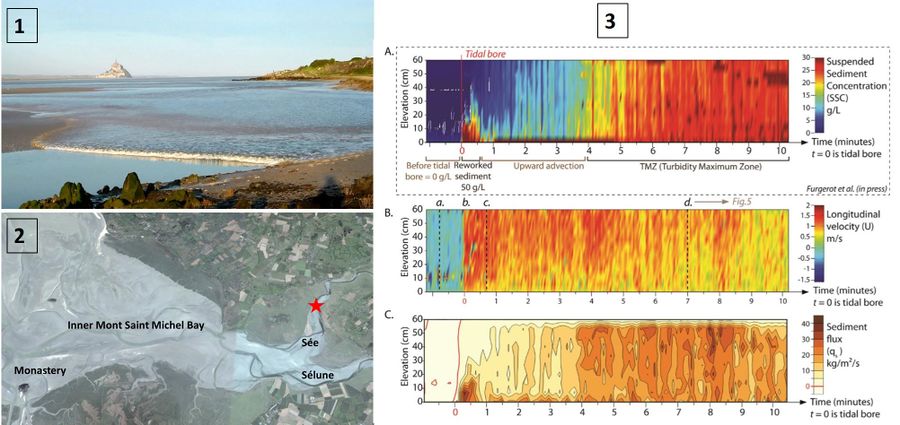
For large Froude numbers, bores correspond to turbulent breaking fronts (Fig. 5), where the energy is dissipated by turbulent eddies[27]. The transition between undular and turbulent bores is shown in Fig. 11. Before arrival of the tidal bore the current velocity is generally low and in the ebb direction. At the arrival of the bore front the current velocity is almost instantaneously reversed into the flood direction and reaches a high value within minutes. Fig. 9 shows the sharp increase in the current velocity and suspended sediment concentration recorded in the megatidal Baie du Mont Saint Michel at spring tide when the tidal flood wave enters the tidal flat area and the small rivers at the head of the Baie [28]. The sudden strong change of the current velocity has an important stirring effect on the bed sediments, causing a sharp increase of the suspended sediment concentration. Turbulent bores contribute significantly to upstream sediment transport[29] and thus play an important role in estuarine morphodynamics. Observations of Tu et al. (2021[30] of the tidal bore in the Qiantang Estuary, China, show that during bore passage the turbulence generated at the bottom by the tidal current is augmented by turbulence injection from the surface as part of the breaking processes of both bore front and the bore associated secondary waves. The injected turbulence enhances vertical mixing and upstream tidal advection of sediments.
In many tidal rivers the bore propagation near the shallow channel banks differs from the bore propagation in the deeper middle part of the channel. The local Froude number is relatively lower at the deeper parts of the channel, where the bore has often an undulating character, while a higher breaking bore occurs in the shallower parts. This phenomenon is illustrated in Fig. 10 for the tidal bore in the Petitcodiac and Kampar rivers.
Modelling
Tidal bore formation involves a large range of temporal and spatial scales, from the scale of the estuary to the turbulence scale. For this reason, it is difficult to integrate all these processes into a comprehensive model, either a physical model (laboratory experiments) or a numerical model.
Physical models
Due to the large range of scales, it is impossible to design a laboratory experiment in close similitude with natural tidal bores. However, leaving aside the tidal wave transformation and bore formation, the bore in itself (i.e. hydraulic jump in translation) can be studied in detail from flume experiments. The bore is commonly generated in a rectangular flume by using a fast-closing gate at the upstream end of the flume[24][19]. This method allows the study of the different bore regimes (see Fig. 11) and provides valuable insights in secondary wave structure and vortical motions.
To avoid the abrupt bore generation of the above method, Rousseaux et al. (2016)[10] proposed a novel approach. This method mimics the tidal asymmetry met in nature between the ebb and the flood. Fig. 12 shows an example of a tidal-like bore generated with this method.

Numerical models
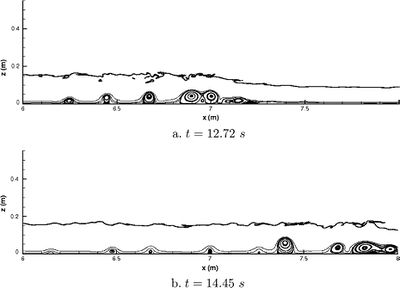
Recent approaches, based on the resolution of the general Navier Stokes equations in their multiphase form (water phase and air phase), allow a detailed description of bore structure, turbulence and air entrainment in a roller at the bore front[31][32]. Figure 13 presents the simulation of recirculating structures under a breaking bore. Navier-Stokes approaches are dedicated to small scale bore processes and cannot be applied to tidal bores at the estuarine scales because of limited computation power. Such applications would require long-wave models, where small scale vorticity motions are parametrized and not directly resolved.
The most common long-wave model is the depth-averaged Saint Venant or Non Linear Shallow Water (NSW) model, which assumes hydrostatic pressure. This model gives a good description of the large-scale tidal wave transformation. The properties of breaking turbulent bores, are also quite well described by the non-dispersive NSW equations with jump conditions [35].
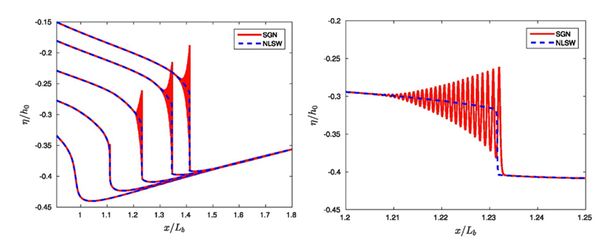
However, the onset of a tidal bore and its evolution upstream is controlled by non-hydrostatic dispersive mechanisms[36]. Although the onset of the tidal bore can be well described by classical weakly dispersive weakly nonlinear Boussinesq-type equations ([36], see Boussinesq equations), the subsequent nonlinear evolution, for high-intensity tidal bores, requires the use of the basic fully nonlinear Boussinesq equations, named Serre-Green Naghdi (SGN) equations[37][34][9]. This modelling approach allows an accurate description of both the tidal bore formation on the estuarine scale (Fig. 4) and the bore structure on the local scale (Fig. 14).
See also
- Tidal asymmetry and tidal inlet morphodynamics
- Ocean and shelf tides
- Morphology of estuaries
- Estuaries
- Dam break flow
- Tsunami
References
- ↑ 1.0 1.1 Bonneton, P, Parisot, J-P., Bonneton, N., Sottolichio, A., Castelle, B., Marieu, V., Pochon, N. and Van de Loock, J. 2011. Large amplitude undular tidal bore propagation in the Garonne River, France, Proceedings of the 21st ISOPE Conference: 870-874, ISBN 978-1-880653-96-8
- ↑ Bartsch-Winkler, S., and Lynch, D. K. 1988. Catalog of worldwide tidal bore occurrences and characteristics. US Government Printing Office
- ↑ Colas, A. 2017. Mascaret, prodige de la marée. Atlantica Editions
- ↑ Furgerot, L. (2014). Propriétés hydrodynamiques du mascaret et de son influence sur la dynamique sédimentaire: Une approche couplée en canal et in situ (estuaire de la Sée, Baie du Mont Saint Michel) (Doctoral dissertation, Caen)
- ↑ 5.0 5.1 5.2 5.3 5.4 Bonneton, P., Bonneton, N., Parisot, J-P. and Castelle, B. 2015. Tidal bore dynamics in funnel-shaped estuaries. J. Geophys. Res.: Ocean 120: 923-941. DOI: 10.1002/2014JC010267
- ↑ Lanzoni, S. and Seminara, G. 1998. On tide propagation in convergent estuaries, J. Geophys. Res. 103: 30793–30812
- ↑ Savenije, H.H.G. 2012. Salinity and Tides in Alluvial Estuaries, second ed., Salinity and Tides in Alluvial Estuaries, second ed., www.salinityandtides.com
- ↑ Dronkers, J. 2017. Convergence of estuarine channels. Continental Shelf Res. 144: 120–133
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 Filippini, A. G., Arpaia, L., Bonneton, P., & Ricchiuto, M. 2019. Modeling analysis of tidal bore formation in convergent estuaries. European Journal of Mechanics-B/Fluids 73: 55-68 Cite error: Invalid
<ref>tag; name "F" defined multiple times with different content - ↑ 10.0 10.1 10.2 Rousseaux, G., Mougenot, J. M., Chatellier, L., David, L. and Calluaud, D. 2016. A novel method to generate tidal-like bores in the laboratory. European Journal of Mechanics-B/Fluids 55:31-38
- ↑ 11.0 11.1 Bonneton, P., Filippini, A.G., Arpaia, L., Bonneton, N. and Ricchiuto, M. 2016. Conditions for tidal bore formation in convergent alluvial estuaries. Estuarine, Coastal and Shelf Science. 172: 121-127 Cite error: Invalid
<ref>tag; name "B16" defined multiple times with different content - ↑ Pan, D. and Li, Y. 2024. Long-Term Impacts of Runoff and Coastal Reclamation on Tidal Bore Variations in the Qiantang River Estuary, China. J. Mar. Sci. Eng. 12, 1983
- ↑ Horrevoets, A. C., Savenije, H. H. G., Schuurman, J. N. and Graas, S. 2004. The influence of river discharge on tidal damping in alluvial estuaries. Journal of Hydrology 294: 213-228
- ↑ Wolanski, E., Williams, D., Spagnol, S. and Chanson, H. 2004. Undular tidal bore dynamics in the Daly Estuary,Northern Australia. Estuarine, Coastal and Shelf Science 60: 629-636
- ↑ Keevil, C. E., Chanson, H. and Reungoat, D. 2015. Fluid flow and sediment entrainment in the Garonne River bore and tidal bore collision. Earth Surface Processes and Landforms 40: 1574-1586
- ↑ Dronkers, J.J. 1964. Tidal computations in rivers and coastal waters. North-Holland Publ. Co., 518 pp.
- ↑ 17.0 17.1 17.2 Lemoine, R. 1948. Sur les ondes positives de translation dans les canaux et sur le ressaut ondulé de faible amplitude. Houille Blanche: 183-185
- ↑ Stoker, J.J. 1957. Water Waves. Interscience, New York
- ↑ 19.0 19.1 Chanson, H. 2009. Current knowledge in hydraulic jumps and related phenomena. A survey of experimental results. European Journal of Mechanics-B/Fluids 28: 191-210
- ↑ Favre, H. 1935. Etude théorique et expérimentale des ondes de translation dans les canaux découverts (Theoretical and experimental study of travelling surges in open channels), Dunod, Paris
- ↑ 21.0 21.1 Chassagne, R., Filippini, A., Ricchiuto, M. and Bonneton, P. 2019. Dispersive and dispersive-like bores in channels with sloping banks. Journal of Fluid Mechanics 870: 595-616. doi:10.1017/jfm.2019.287
- ↑ Binnie, A. M., & Orkney, J. C. (1955). Experiments on the flow of water from a reservoir through an open horizontal channel II. The formation of hydraulic jumps. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 230(1181), 237-246
- ↑ Chanson, H. (2010). Undular tidal bores: basic theory and free-surface characteristics. Journal of Hydraulic Engineering, 136(11), 940-944
- ↑ 24.0 24.1 Treske, A. 1994. Undular bore (Favre-waves) in open channels - Experimental studies, J. Hydraulic Res. 32: 355-370
- ↑ Bonneton, P., Van de Loock, J., Parisot, J-P., Bonneton, N., Sottolichio, A., Detandt, G., Castelle, B., Marieu, V. and Pochon, N. 2011. On the occurrence of tidal bores – The Garonne River case. Journal of Coastal Research, SI 64: 11462-1466
- ↑ Bonneton, N., Bonneton, P., Parisot, J-P., Sottolichio, A. and Detandt G. 2012. Tidal bore and Mascaret - example of Garonne and Seine Rivers. Comptes Rendus Geosciences, 344, 508-515
- ↑ Tu, J. and Fan, D. 2017. Flow and turbulence structure in a hypertidal estuary with the world's biggest tidal bore. Journal of Geophysical Research: Oceans, 122: 3417-3433
- ↑ 28.0 28.1 Furgerot, L., Mouazé, D., Tessier, B., Perez, L., Haquin, S., Weill, P., & Crave, A. (2016). Sediment transport induced by tidal bores. An estimation from suspended matter measurements in the Sée River (Mont-Saint-Michel Bay, northwestern France). Comptes Rendus Géoscience, 348(6), 432-441
- ↑ Reungoat, D., Lubin, P., Leng, X. and Chanson, H. 2018. Tidal bore hydrodynamics and sediment processes: 2010–2016 field observations in France. Coastal Engineering Journal 60: 484-498
- ↑ Tu, J., Fan, D. and Voulgaris, G. 2021. Field observations of turbulence, sediment suspension, and transport under breaking tidal bores. Marine Geology 437, 106498
- ↑ 31.0 31.1 Lubin, P., Chanson, H. and Glockner, S. 2010. Large eddy simulation of turbulence generated by a weak breaking tidal bore. Environmental Fluid Mechanics 10: 587-602
- ↑ Berchet, A., Simon, B., Beaudoin, A., Lubin, P., Rousseaux, G. and Huberson, S. 2018. Flow fields and particle trajectories beneath a tidal bore: A numerical study. International Journal of Sediment Research 33: 351-370
- ↑ Soares-Frazão S. and Zech Y. 2002. Undular bores and secondary waves - Experiments and hybrid finite-volume modeling. Journal of Hydraulic Research, International Association of Hydraulic Engineering and Research (IAHR) 40: 33-43
- ↑ 34.0 34.1 Tissier, M., Bonneton, P., Marche, F., Chazel, F., & Lannes, D. 2011. Nearshore dynamics of tsunami-like undular bores using a fully nonlinear Boussinesq model. Journal of Coastal Research SI 84: 603-607
- ↑ Chanson, H. 2012. Tidal bores, aegir, eagre, mascaret, pororoca: Theory and observations. World Scientific
- ↑ 36.0 36.1 Peregrine, D. H. 1966. Calculations of the development of an undular bore. Journal of Fluid Mechanics 25: 321-330
- ↑ Bonneton, P., Barthélemy, E., Chazel, F., Cienfuegos, R., Lannes, D., Marche, F. and Tissier, M. 2011. Recent advances in Serre–Green Naghdi modelling for wave transformation, breaking and runup processes. European Journal of Mechanics-B/Fluids 30: 589-597
Please note that others may also have edited the contents of this article.
|