Analysis of coastal processes with Empirical Orthogonal Functions
Contents
Applications of Empirical Orthogonal Functions (EOF)
The application of Principal Component Analysis (PCA) to the analysis of morphological datasets is generally termed EOF, Empirical Orthogonal Functions. EOF methods have been used with success to analyze nearshore beach topography, as will be described below. However, the technique may not be appropriate for studies of bar dynamics as eigenfunctions are fixed in space since bars, on the contrary, are wave-like patterns that travel in time. Extended EOFs and Complex Principal Component Analysis, both modifications of EOFs, do not have such shortcoming; however, they rely on time-lagged data, and thus the data needs to be sampled at constant time intervals. This is not usual in coastal applications, as noted by Larson et al. (2003), but may be achieved via data interpolation.
Larson et al. (2003)[1] cite three papers (Hayden et al. 1975 [2], Winant et al., 1975 [3] and Aubrey et al., 1979[4]) as pioneering applications of EOFs in coastal morphology, in particular for beach profile behavior. These researchers, as Larson et al. (2003) point out, observed that the lower order EOF modes could be related to particular coastal features, i.e. the mean profile, bars and berms, and low-tide terraces to the first, second and third order modes, respectively. Therefore, these studies also constitute first attempts of coastal characterization via EOFs. The EOF method together with a moving window model were used by Wijnberg and Terwindt (1995) [5] to divide the Dutch coast into regions according to their characteristic patterns of behavior. They analyzed 115 kms of Dutch coast via 14 thousand transects extending about 800 m cross-shore at generally 250 m longshore intervals. These regions vary from 5 to 42 kms in size, each characterized mainly by what the authors define as ‘secondary’ features, i.e. features diverging from the mean profile such as mounds or sandbars (this example and those mentioned below are such that the mean has not been removed from the data). The authors observed sub-decadal shifts of shoreline positions and speculate this could be related to sandbar dynamics. Larson et al. (2003) applied the same technique of Wijnberg and Terwindt (1995) to nearshore topography in a Dutch and a German coastal area. For the Dutch coastal site, the modes were related to the coastal features, with similar results as in Aubrey (1979) except that the third EOF was shifted 90 degrees in phase with respect to the second, being also related to the bar system. For the German site, the technique was applied to study beach nourishment effects on topography evolution at a beach resort that has suffered from severe erosion in the past (Dette and Newe, 1997).[6] In this case the first EOF indicated an increase in mean elevation. Similarly to other EOF analysis at other sites infilled sites, rapid changes occur at the beginning and were then followed by gradual adjustment to an equilibrium. In general the process takes one year if beach nourishment is nearshore, or considerably longer if the beach nourishment is at the berm, as Larson et al. (2003) observed.
Application of Singular Spectrum Analysis (SSA)
A particular modification of Principal Component Analysis (PCA), namely Singular Spectrum Analysis (SSA), has been used to identify chaotic properties of a system, that is, to determine the number (embedding dimension) of independent variables that are needed to describe the system, and the properties of the attractors in such a system. SSA was extensively discussed by Southgate et al. (2003[7]), and the main points raised by the authors are summarized here. An introduction to the mathematical background is given in the appendix. In the case of SSA the data matrix has in its columns not the full original measured time series, but the data at successive equitemporal lags, up to the maximum shift needed for a full system’s description. The number of columns of the data matrix defined as such is called the embedding dimension, [math]M[/math], and the SSA will not resolve periods longer than that corresponding to [math]M[/math]. It is of interest to note that the SSA technique is used not only for chaotic characterization studies, but also for noise reduction, data detrending, oscillatory characterization, or forecasting. Example applications to coastal morphology, given by Southgate et al. (2003[7]), relate to long-term shoreline evolution. However, in general this technique has not been applied to coastal research, but rather to climatology (e.g. Ghil et al., 2002 [8]).
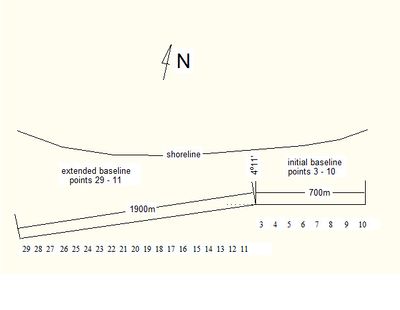
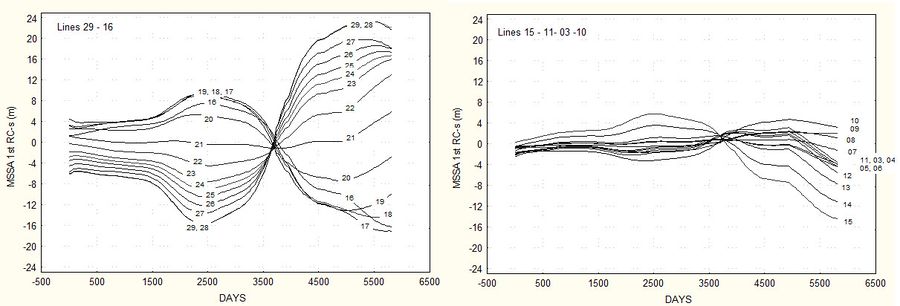
EOF can be generalized to Extended EOF (EEOF) for data sets containing many spatial points and few time realizations. For data sets where the number of spatial points is less than the number of realizations SSA can be generalized to Multi-channel SSA (MSSA). An example of application of the MSSA method was presented by Różyński (2005) [9], who analyzed shoreline variations from 1983 until 1999, sampled monthly at 27 equally spanned transects, covering a stretch of 2,600 m of an open sea coastal segment in Poland, transects 29-11 and 03-10, see Fig. 1. The study revealed three important patterns representing shoreline standing waves. Upon locations of their nodes, the wavelengths of these standing waves could be directly evaluated. Next, the magnitudes of the variation of antinodes were used for the assessment of their amplitudes. Finally, the periods were established by determination of the time needed by antinodes to evolve from maximum seaward to maximum landward position. The largest standing wave had the wavelength of 1,500 m with amplitudes ranging between 4 and 20 m about the mean shoreline position at a given transect and the corresponding period of more than 32 years, see Fig. 2. No firm explanation for the existence of this wave could be provided. Physical mechanisms that may produce standing shoreline waves are discussed in the article Rhythmic shoreline features.
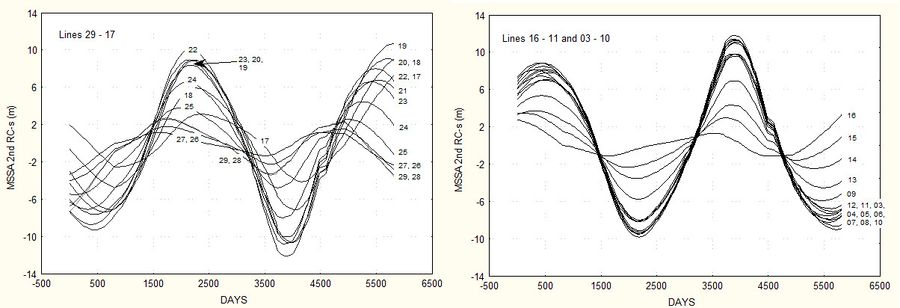
The 2nd wave had the wavelength in the range of 1,000-1,400 m, amplitudes of 10 m and the period of 8 years, see Fig. 3. Later studies, Różyński (2010) [10] and Różyński (2015) [11], identified a coupling of this standing wave to variations of the winter index of North Atlantic Oscillation (for Dec., Jan., Feb. and Mar.), which contains a significant component with the period of 8 years and was found to be controlling winter wave climates and water levels in the Baltic Sea to a considerable degree.
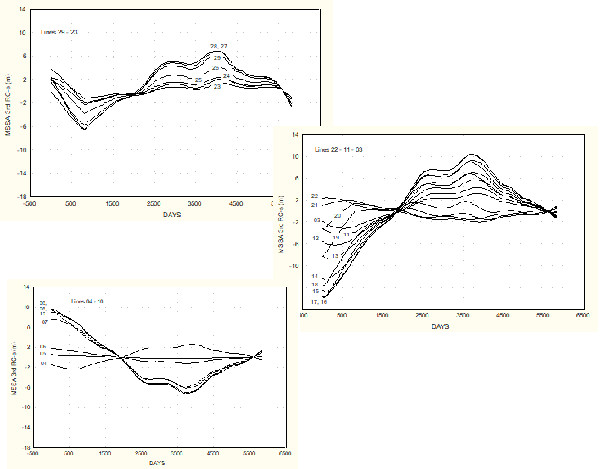
The 3rd standing wave was found to be less regular; the estimated wavelength fell between 1,400 – 1,600 m, the amplitudes varied from 10 m at one anti-node to only 6 m at the other, see Fig. 4. The processes responsible for the presence of this wave could not be identified in the absence of records of long-term hydrodynamic background.
Application of Principal Oscillation Patterns and PIP
In a Principal Oscillation Pattern (POP) analysis the data is analyzed using patterns based on approximate forms of dynamical equations, so it may be used to identify changing patterns, such as standing waves and migrating waves (Larson et al, 2003)[1]. POP is a linearized form of the more general Principal Interaction Pattern (PIP) analysis. A POP analysis using the long-term Dutch JARKUS dataset of cross-shore beach profiles (Jansen, 1997[12]) showed that POP systematically lost 4% to 8% more data than an EOF analysis. The prediction method was optimised using 8 POPs as adding more POPS included more of the noise. Różyński and Jansen (2002)[13] applied POP analysis to 4 beach profiles at Lubiatowo (Poland) and recommended that an EOF analysis be carried out first.
Appendix: Introduction to PCA, EOF and SSA methods
A: Principal Component Analysis (PCA)
Principal Component Analysis is a data analysis method intended to identify the most important patterns in large data sets, i.e. the patterns that represent the most important variance in the data. The PCA method has first been developed by Pearson (1901)[14] and Hotelling (1933)[15].
Consider a dataset [math]\; h(x_i,t_m) = h_{im}, \; i = 1, .., N_x; \; m = 1, .., N_t \;[/math] consisting of a number of [math]N_t[/math] successive observations of a set of [math]N_x[/math] variables. The most important patterns in the dataset are represented by a limited number of principal components, each representing a pattern of temporal variation in the variables of a certain order of magnitude. The principal component of the first order represents the largest pattern of variation, the principal component of the second order represents the second largest pattern of variation after the first order variation is subtracted, and so on. The essential difference between PCA and data analysis methods such as decomposition according to Fourier or wavelet components is that in this case the principal components are not based on predetermined shape functions, but on shape functions that are derived from the data set itself. This allows the dataset to be rather well reproduced with only a small number of principal components; in practice, two or three principal components are often sufficient.
In PCA the shape functions are not continuous; they are formed by a set of [math]N_x[/math] normalized orthogonal weight vectors [math]\; \bf e^{(k)}, \;[/math][math]\; k = 1,2, .., N_x \;[/math] with each the same number of dimensions [math]N_x[/math] as the set of variables. The elements of these weight vectors are indicated by [math]\; e_{ki} \;[/math] and have the property
[math]\; \sum_{i=1}^{N_x} e_{ki} e_{li} \, = \, \delta_{kl} \, = \, \sum_{i=1}^{N_x} e_{ik} e_{il} . \qquad (A1)[/math]
The dataset can be described by a matrix [math]\; \bf D \;[/math] with elements [math]\; d_{im}=h_{i,m} - \overline h_i \;[/math], where [math]\; \overline h_i \;[/math] is the average over all [math]\; m=1, ..,N_t \;[/math] observations. The principal component of order [math]\; k [/math] is represented by the [math]N_t[/math]-dimensional vector [math]\; \bf z^{(k)} \;[/math] with elements
[math]\; z_{km} = \sum_{i = 1}^{N_x} \; d_{im} \; e_{ki} . \qquad (A2)[/math]
The numbers [math]e_{ki}[/math] are the components of the eigenvectors [math]\; \bf e^{(k)} [/math] of the [math]N_x*N_x[/math] covariance matrix [math]\; \bf C = D^T D [/math] with elements [math]c_{ij}[/math],
[math]\; c_{ij}=\sum_{m = 1}^{N_t} d_{im} d_{jm}. \qquad (A3)[/math]
The corresponding eigenvalues [math]\lambda_k[/math] are given by
[math]\sum_{j = 1}^{N_x} \; c_{ij} \; e_{ki} = \lambda_k \; e_{kj} . \qquad (A4)[/math]
The eigenvalues are positive (because the covariance matrix [math]\; \bf C[/math] is symmetric) and ordered such that [math]\lambda_1 \gt \lambda_2\gt …. \gt \lambda_{Nx}[/math]. The first order principal components [math]\; z_{1j} [/math] describes the greatest pattern of variation in the data set. Routine mathematical procedures can be used to determine the eigenvectors.
The eigenvalues sum up to the total signal variance, i.e. the sum of the terms along the main diagonal of [math]\mathbf C[/math]. They show the distribution of variance among eigenvectors, thus indicating their importance. From a practical point of view several key modes normally contain at least 90% of the total variance, so the most important features of a studied system can be identified. However, it must be emphasized that the principal components are based on correlations, which do not necessarily represent cause-effect relationships.
The first-order principal component [math]\; \bf z^{(1)}[/math] has [math]N_t[/math] time components
[math]z_{1m} = \sum_{i=1 }^{N_x} \; d_{im} \; e_{1i}. \qquad (A5)[/math]
The second-order principal component [math]\;\bf z^{(2)} [/math] corresponds to the eigenvector with the second highest eigenvalue of the covariance matrix (A3). And so on for the third-order principal component. Most information on the major underlying dynamical processes is often contained in the first two or three principal components. Thus, when reconstructing the original data from the principal components [math]\; \bf z^{(k)}[/math] using Eq. (A1),
[math]d_{im}=\sum_{k=1}^{N_x} \; z_{km} \; e_{ki} , \qquad (A6)[/math]
then a reasonable approximation is obtained if only the first few components [math]z_{km}[/math] are retained.
The principal components are most influenced by the data [math]\; d_{im} \equiv d(x_i,t_m) \;[/math] with the strongest time variation, i.e. with the greatest variance [math]\; c_{ii}=\sum_{m = 1}^{N_t} d_{im}^2 \,[/math]. The PCA therefore tends to be biased towards the data with the greatest variance. This bias can be avoided by dividing the data by the square root of the variance. Another bias may arise when the time variation is dominated by a phase shift between successive datasets. Therefore, phase shifts between successive datasets (propagating signal) should be removed before applying PCA. A more detailed explanation of the mathematical background of the PCA data analysis methods is given in the Wikipedia article PCA.
B: Empirical Orthogonal Functions (EOF)
Some key mathematical details of the EOF analysis method of two-dimensional spatial data are presented below. In sum, it should be underlined that the EOF, as well as the Singular Spectrum Analysis (SSA), Extended EOF (EEOF) and Multi-channel SSA (MSSA) methods, are all variants of the same PCA methodology, based on the covariance structure of a studied system.
In the EOF variant the system matrix is composed of covariances of a studied parameter/quantity at two points of the domain at the same moments in time. For example, when the seabed is sampled [math]N_t[/math] times, the measurements usually consist of [math]N_y[/math] cross-shore profiles with [math]N_x[/math] sampling points in each of them. The dataset is described by a matrix [math]\; \bf D \;[/math] with elements [math]\; d_{im}=h_{i,m} - \overline h_i \;[/math], where [math]\; \overline h_i \;[/math] is the average over all [math]\; m=1, ..,N_t \;[/math] observations. The resulting lag-0 covariance matrix [math]\mathbf C[/math] with elements [math]c_{i,j}[/math] has [math]N_{xy}=N_x*N_y[/math] terms, where [math]N_{xy}[/math] is the number locations of the data grid:
[math]c_{i,j} = \sum_{m=1}^{N_t} \; d_{im} d_{jm} , \qquad (B1)[/math]
with [math]i,j = 1, .... , N_{xy}[/math]. Note that this is identical to Eq. (A3). Each index value [math]i[/math] corresponds to a particular point of the [math]N_x*N_y[/math] data grid, and the same holds for each [math]j[/math]. For [math]i=j[/math] (main diagonal) the terms represent variances. The eigenvectors [math]\mathbf e^{(k)}[/math] with components [math]e_{ki}[/math] and eigenvalues [math]\lambda_k[/math] are defined by
[math]\sum_{j=1}^{N_{xy}} c_{ij} e_{kj} = \lambda_k e_{ki} ,\; i=1, ..n. \qquad (B2)[/math]
The eigenvectors [math]\mathbf e^{(k)}[/math] are orthogonal and scaled to unit length, [math]\sum_{j=1}^{N_{xy}} e_{kj} e_{lj} = \delta_{kl}[/math] and the eigenvalues ranked in decreasing order of magnitude. The vectors [math]\mathbf e^{(k)}[/math] represent the spatial side of the EOF decomposition; when plotted in the real physical space (e.g. the studied seabed domain), the components [math]e_{ki}[/math] indicate the areas of highest variability.
The principal components [math]\mathbf z^{(k)}, \; k=1, .., N_{xy}[/math] (temporal side of EOF decomposition) can be obtained using the following projections:
[math]z_{km}=\sum_{i=1}^{N_{xy}} \; d_{im} \; e_{ki} , \qquad (B3)[/math]
where [math]z_{km}[/math] denotes the [math]m[/math]-th moment in time ([math]m=1, .., N_t[/math]) of the [math]k[/math]-th principal component [math]\mathbf z^{(k)}[/math], associated with the [math]k[/math]-th eigenvector [math]\mathbf e^{(k)}[/math]. Very importantly, its variance is equal to [math]\lambda_k[/math]. As for principal component analysis, each pair [math]\mathbf z^{(k)}[/math] and [math]\mathbf e^{(k)}[/math] provides information on the spatiotemporal evolution of the [math]k[/math]-th EOF mode.
C: Singular Spectrum Analysis (SSA)
In the SSA method the spatial dimension is reduced to a single point: [math]N_x N_y = 1[/math]. The focus is on analyzing the temporal variation in the observed time series [math]d_n = h_n -\overline h, \; n=1, .., N[/math] from which the temporal average [math]\overline h = 0[/math] has been removed. For this purpose, the lagged covariance matrix is built:
[math]\mathbf{C} = \begin{bmatrix} c(0) & c(1) & c(2) & \cdots & c(M-1) \\ c(1) & c(0) & c(1) & \cdots & c(M-2) \\ \vdots & \vdots & \vdots & & \vdots \\ c(M-1) & c(M-2) & c(M-3) & \cdots & c(0) \end{bmatrix} [/math]
with the terms:
[math]c(n)=\frac{1}{N - n} \sum_{m=1}^{N-n} \; d_m \; d_{m+n} , \qquad (C1)[/math]
where [math]d_n[/math] is the value of [math]d[/math] at time [math]t_n[/math]. The parameter [math]M[/math] is called either window length or embedding dimension and determines the maximum covariance lag; a practical rule of thumb suggests that [math]M \le N/3 \;[/math] ([math]N[/math] is the total number of successive observations). The matrix [math]\mathbf C[/math] is symmetrical and has positive eigenvalues; if one or more eigenvalues are zero then the signal contains a deterministic component, represented by a perfect sine function. Formally, we can compute the orthonormal eigenvectors [math]\mathbf e^{(k)}[/math] and principal components [math] \mathbf{z^{(k)}}[/math] of this matrix. The latter are derived from the formula:
[math]z_{k,n}=\sum_{m=1}^{M} \; d_{m+n-1} \; e_{km}[/math] for [math]1 \le n \le N-M +1 . \qquad (C2)[/math]
Thus, we have to take [math]M[/math] elements of the original series [math]\mathbf d[/math] from [math]m[/math]-th to [math](m+M)[/math]-th element, compute their products with the corresponding elements of the eigenvectors [math]\mathbf e^{(k)}[/math] of the matrix [math]\mathbf C[/math] and sum these products to obtain the [math]n[/math]-th element of the [math]k[/math]-th principal component. Hence, the principal components are time series of the length [math]N – M[/math]. Importantly, despite being orthogonal, the prinicipal components are not correlated only at lag zero. Because [math]M[/math] consecutive elements of the original series are needed to compute one term of every principal component, the correlation structure of the original series must be imprinted in the principal components. Moreover, there may be up to [math]M[/math] subsets of the original time series containing the specific element [math]d_{m+n}[/math], so there may be up to [math]M[/math] different ways of reconstructing this element with principal components:
[math]d_n=\sum_{k=1}^{M} \; z_{k,n-m+1} \; e_{km} , \qquad (C3)[/math]
with [math]1 \le n \le N, \; 1 \le n-m+1 \le N-M+1 .[/math] (Relation (C3) is obtained through multiplication of (C2) by [math]e_{km'}[/math], summing over [math]k[/math], using [math]\sum_{k=1}^M e_{km} e_{km'} = \delta_{mm'}[/math] and changing indices [math]m+n-1 \longrightarrow n[/math]). Thus, using principal components we do not obtain a unique expansion of the original series. However, uniqueness can be established when we calculate the mean values of all possible ways of reconstructing the original signal:
[math] d_{k,n} =\frac{1}{M} \sum_{m=1}^{M} \; z_{k,n-m+1} \; e_{km} \qquad (C4)[/math]
for [math]M \le n \le N – M +1[/math] at the middle part of the signal,
[math] d_{k,n} =\frac{1}{n} \sum_{m=1}^{n} \; z_{k,n-m+1} \; e_{km} \qquad (C5)[/math]
for [math]1 \le n \le M -1[/math] at the beginning of the signal,
[math] d_{k,n} =\frac{1}{N - n +1} \sum_{m=n - N + M}^{M} \; z_{k,n-m+1} \; e_{km} \qquad (C6)[/math]
for [math]N-M +2\le n \le N [/math] at the end of the signal.
There are [math]M[/math] quantities [math]\mathbf d^{(k)}[/math], which are termed reconstructed components and provide a unique expansion of the original signal. They are additive, but not orthogonal, so their variances are not cumulative. Therefore, a researcher should investigate not only single reconstructed components, but also their subsets in search for plausible interpretation of signal constituents. Traditional time series analysis techniques, mostly the Fourier analysis are used for this purpose. Usually, the entire useful information is contained in a few reconstructed components, so the analysis is not as tedious as might be suspected.
Finally, both the EEOF and MSSA methods provide unique expansions of the studied signals in time and space as well. Both methods are identical and differences in terminology are mostly practical; the term EEOF is used when [math]N_{xy} \equiv N_x *N_y \gg N_t[/math], whereas MSSA is referred to when [math]N_t \gt N_{xy}[/math]. The resulting block system matrix is presented below:
[math]\mathbf{T} = \begin{bmatrix} T_{1,1} & T_{1,2} & \cdots & T_{1, N_{xy}} \\ T_{2,1} & T_{2,2} & \cdots & T_{2, N_{xy}} \\ \vdots & \vdots & \ddots & \vdots \\ T_{ N_{xy}, 1} & T_{ N_{xy}, 2} & \cdots & T_{ N_{xy}, N_{xy}} \end{bmatrix} [/math]
The main diagonal contains auto-covariance matrices of all [math]N_{xy}[/math] signals involved, the remaining (block) terms represent cross-covariances among them. Formally, this matrix can be manipulated analogously to previous description, so that [math]M[/math] reconstructed components are obtained. However, we should keep in mind that their interpretation can be difficult, because of the number of spatial points considered. Therefore, caution is recommended when applying these advanced techniques; such analysis should be preceded by ordinary EOF/SSA studies, depending on the problem studied.
Related articles
References
- ↑ 1.0 1.1 Larson, M., Capobianco, M., Jansen, H., Rozynski, G. N., Stive, M., Wijnberg, K. M. and Hulscher, S. 2003. Analysis and modeling of field data on coastal morphological evolution over yearly and decadal time scales. Part 1: Background and linear techniques. Journal of Coastal Research 19: 760-775
- ↑ Hayden, B., Felder, W., Fisher, J., Resion, D., Vincent, L. and Dolan, R. 1975. Systematic variations in inshore bathymetry. Technical report No. 10, Department on Environmental Sciences, University of Virginia, Virginia, USA.
- ↑ Winant, C. D., Inman, D. L. And Nordstrom, C. E. 1975. Description of seasonal beach changes using empirical eigenfunctions. Journal of Geophysical Research 80: 1979-1986
- ↑ Aubrey, D. G., Inman, D. L. and Winant, C. D. 1979. Seasonal patterns of onshore/offshore sediment movement. Journal of Geophysical Research 84: 6347-6354
- ↑ Wijnberg K. M. and Terwindt J. H. J. 1995. Extracting decadal morphological behavior from high-resolution, long-term bathymetric surveys along the Holland coast using eigenfunction analysis. Marine Geology 126: 301-330
- ↑ Dette, H. H. and Newe, J. 1997.Depot beach fill in front of a cliff. Monitoring of a nourishment site on the Island of Sylt 1984-1994. Draft Report, Leichweiss Institute, Technical University of Braunschweig, Braunschweig, Germany.
- ↑ 7.0 7.1 Southgate, H.N., Wijnberg, K.M., Larson, M., Capobianco, M. and Jansen, K. 2003. Analysis of Field Data of Coastal Morphological Evolution over Yearly and Decadal Timescales. Part 2: Non-Linear Techniques. Journal of Coastal Research 19: 776–789
- ↑ Ghil M., R. M. Allen, M. D. Dettinger, K. Ide, D. Kondrashov, M. E. Mann, A. Robertson, A. Saunders, Y. Tian, F. Varadi, and Yiou, P. 2002. Advanced spectral methods for climatic time series. Reviews in Geophysics 40: 3.1-3.41
- ↑ Różyński, G. 2005. Long term shoreline response of a non-tidal, barred coast. Coastal Engineering 52: 79-91
- ↑ Różyński, G. 2010. Long-term evolution of Baltic Sea wave climate near a coastal segment in Poland; its drivers and impacts. Ocean Engineering 37: 186-199
- ↑ Różyński, G. 2015. Long-term couplings of winter index of North Atlantic oscillation and water level in the Baltic Sea and Kattegat. Ocean Engineering, 109: 113–126
- ↑ Jansen, H. 1997. POP analysis of the JARKUS dataset: the IJmuiden-Katwijk section. Fase 2 Report, Project RKZ-319, Delft Univ. Technology, Netherlands.
- ↑ Różyński, G. and Jansen, H. 2002. Modeling Nearshore Bed Topography with Principal Oscillation Patterns. J. Wtrwy., Port, Coast., and Oc. Engrg. 128: 202-215
- ↑ Pearson, K. 1901. On Lines and Planes of Closest Fit to Systems of Points in Space. Philosophical Magazine. 2 (11): 559–572
- ↑ Hotelling, H. 1933. Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417-441, and 498-520
Please note that others may also have edited the contents of this article.
|