Beach Cusps
Contents
Introduction
Beach cusps are one of the most commonly observed shoreline features of sandy and gravel beaches. They appear at the edge of the so-called swash zone, the part of the beach where waves have collapsed into a thin bore that runs up and down the shore (see Swash zone dynamics). Beach cusps are characterized by highs and lows in elevation with a spacing that, depending on beach slope and incoming wave field characteristics, can vary from less than one meter to 50-100 meters (Figure 1). The highs in elevation are usually called “beach cusp horns” and are essentially a ridge of sediment that protrudes towards the sea with a right angle to the shore. The lows, usually defined as “beach cusp embayments” (or simply bays), tend to be much smoother in elevation and are characterized by a gentler cross-shore slope. Beach cusps appear under a wide variety of hydrodynamic conditions (Holland 1988[1]), from calm to almost stormy conditions, and sediments sizes from fine sand to gravel. Usually, beach cusps are associated to steeper beaches with coarse-grained sediments and normally incident waves. Overall, beach cusps are probably one of the most intriguing and striking patterns in the nearshore.
Flow and sediment characteristics
When normally approaching waves run up the beach and encounter a beach cusp field, the flow diverges at the horns and converges into the bays (Figure 2, left panel) where the water is concentrated before running down the beach (Figure 2 right panel). Narrow, concentrated and offshore-directed flows in the embayments are a typical feature of beach cusps. Other types of circulation patterns around beach cusps have also been reported and for a thorough discussion the reader should refer to Masselink and Pattiaratchi (1998)[2]. From a sedimentological perspective, beach cusps have been observed to develop on gravel and sandy beaches. When sand and gravel are present or when the sand distribution covers fine and coarse sands, the coarser sediment fractions concentrate on the horns of the beach cusps.
Theories of beach cusp formation
Probably because of their impressive regularity, beach cusps have attracted the attention of many scientists and a variety of mechanisms have been suggested since the beginning of the past century (see Coco et al., 1999[3] for details and references to theories that have not survived field evidence or that lack generality). Over more recent times, two theories have emerged to explain the conditions that lead to the development of beach cusps and to predict their geometry (primarily the spacing between beach cusp horns). The two contrasting hypotheses suggest that beach cusps are the result of either (Theory 1) self-organization through sediment-flow feedbacks (Werner and Fink, 1993[4]) or (Theory 2) a pattern in the hydrodynamics due to the presence of standing edge waves (Guza and Inman, 1975[5]).
Self-organization
This approach is based on the idea that feedbacks between flow, sediment transport and morphological change can lead to the development of regular features like beach cusps. The approach has already been successfully applied to a variety of other coastal bedforms ranging from ripples to sand waves, from sandbars to shoreface-connected ridges (see Stability models, Wave ripples, Rhythmic shoreline features, Sand ridges in shelf seas). In the case of beach cusp formation the positive feedbacks that lead to bedform growth is actually quite simple and almost intuitive: once an area of lower elevations starts to develop at some location, the surrounding flow will start to be directed towards it, accelerate and enhance erosion. In fact, such a low area, because of the non-linear relation with sediment transport, will be characterised by greater sediment divergence than the surroundings leading to a positive feedback that increases the relief of the feature and the development of beach cusp bays. Opposite behaviour can be observed on depositional areas (the incipient beach cusp horns) where a slowing flow will cause further deposition of sediment and flow diversion. The switch from positive into negative feedback occurs when the amounts of net sediment erosion or deposition are sensibly reduced because of the beach cusp shape which, once a certain ratio between spacing and amplitude is reached, reduces deceleration and acceleration effects. Finally, the topography does not experience further strong changes and a steady state can be reached.
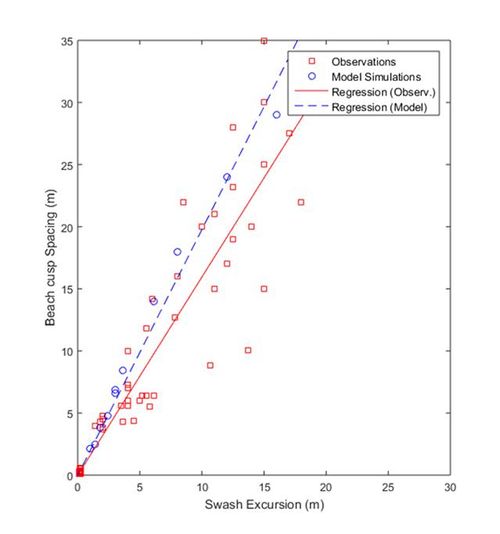
These feedbacks have been tested through numerical models (Werner and Fink, 1993[4]; Coco et al., 2000[6]) and numerical simulations (in agreement with field observations, Coco et al., 1999[3]), indicate that the beach cusp spacing is linearly dependent on the swash excursion (Figure 3). The model simulating beach cusp formation is a radical simplification of the complicated processes that operates in the swash zone, and many of such complications are bypassed by using a cellular type of approach. Nevertheless, the model can simulate also conditions that, in agreement with observations, are not conducive to beach cusp formation or that lead to a less regular pattern growth. The model also simulates conditions that lead to beach cusp disappearance (e.g., the presence of a strong longshore component in the flow). The model and the role of positive and negative feedbacks have also been studied through field observations (known as DozerDuck) where a number of cusps were destroyed by a bulldozer and conditions monitored while cusps reformed (Coco et al., 2003[7] and 2004[8]).
Edge waves
This approach is strongly based on our knowledge of fluid dynamics, which shows that under monochromatic waves approaching at small angles, edge waves may develop: longshore periodic gravity waves trapped close to the shoreline by refraction. These motions, with the largest amplitude at the shoreline, usually propagate in the alongshore direction but can also form a standing pattern with a periodic sequence of high and low amplitudes in the alongshore. These standing edge-wave patterns are assumed to become imprinted on the shoreline giving rise to beach cusps. The mechanism leading to the appearance of edge waves is related to a transfer of energy from reflected incident waves normally approaching a planar beach (Guza and Davis, 1974[9]) and allows prediction of beach cusp spacing as a function of incident wave period, beach slope and edge wave mode. Each mode reflects a different cross-shore structure in amplitude variation and mode zero is assumed to be the most likely to be excited (Guza and Davis, 1974[9]).
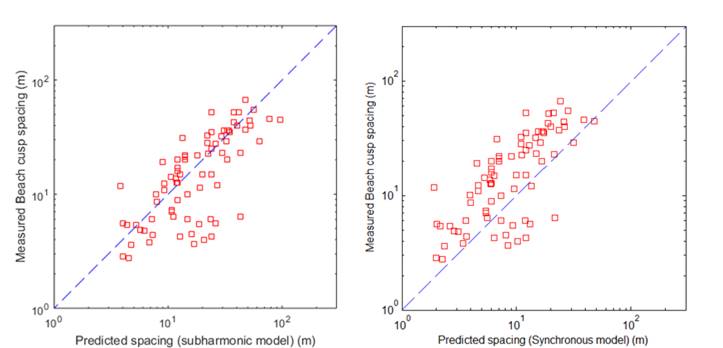
Two types of standing edge waves are considered likely to develop: synchronous and subharmonic, with frequencies the same or half the frequency of the incident wave field, respectively. The alongshore structure of a subharmonic standing edge wave, combined with incident waves, presents a number of nodes (where wave run-up is minimized and where horns are likely to develop) and antinodes (where wave run-up is maximized and bays are likely to be scoured). Edge wave predictions of beach cusp spacing compare reasonably well with a large number of field and laboratory observations (Figure 4, Coco et al., 1999[3]). Although observed beach cusp spacing and edge wave predictions are somehow consistent with the subharmonic predictions (discrepancies are larger for synchronous predictions, see Figure 4), no subharmonic or synchronous standing edge wave was directly measured in any of the data used in Figure 4. Edge wave presence and alongshore structure was inferred from incident wave conditions (sometimes collected in deep water). Aside from the difficulty in measuring the presence of subharmonic standing edge waves (Guza and Bowen, 1981[10], show that large-amplitude beach cusps detune edge wave motions rendering their detection even more complicated), theoretical analysis shows that friction is likely to suppress subharmonic motions (Guza and Bowen, 1976[11]). Recent numerical work (Dodd et al., 2008[12]) appears to indicate that beach cusp formation could be more likely related to the presence of synchronous edge wave motions.
Related articles
References
- ↑ Holland, K.T., 1998, Beach cusp formation and spacings at Duck, USA, Continental Shelf Res., 18, 1081-1098.
- ↑ Masselink, G., and Pattiaratchi, C.B., 1998, Morphological evolution of beach cusp morphology and associated swash circulation patterns, Mar. Geol., 146, 93-113.
- ↑ 3.0 3.1 3.2 3.3 Coco, G., O'Hare, T.J., and Huntley, D.A., 1999, Beach cusps: a comparison of data and theories for their formation, J. Coastal Res., 15(3), 741-749.
- ↑ 4.0 4.1 Werner, B.T., and Fink, T.M., 1993, Beach cusps as self-organised patterns, Science, 260, 968-971.
- ↑ Guza, R.T. and Inman, D.L., 1975, Edge waves and beach cusps, J. Geophys. Res., 80(21), 2997-3012.
- ↑ Coco, G., Huntley, D.A., and O'Hare, T.J., 2000, Investigation of a self-organisation model for beach cusp formation and development, J. Geophys. Res., 105(C9), 21991-22002.
- ↑ Coco, G., Burnet, T.K., Werner, B.T., and Elgar, S., 2003, Test of self-organization in beach cusp formation, J. Geophys. Res., 108(C3), 3101, 46.1-46.11.
- ↑ Coco, G., Burnet, T.K., Werner, B.T., and Elgar, S., 2004, The role of tides in beach cusp development, J. Geophys. Res., 109(C4), C04011, doi: 10.1029/2003JC002154.
- ↑ 9.0 9.1 Guza, R. T. and Davis, R. E., 1974, Excitation of edge waves by waves incident on a beach, Jour. Geophys. Res., 79, 1285-91.
- ↑ Guza, R.T. and Bowen, A.J., 1981, On the amplitude of beach cusps, J. Geophys. Res., 80(21), 4125-4132.
- ↑ Guza, R.T., and Bowen, A.J., 1976, Finite amplitude edge waves, J. Marine Res., 34, 269-293.
- ↑ Dodd, N., Stoker, A. M., Calvete, D., and Sriariyawat, A., 2008, On beach cusp formation. Journal of Fluid Mechanics, 597, 145-169.
Please note that others may also have edited the contents of this article.
|