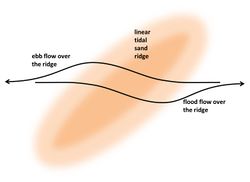
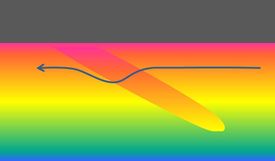
Sand ridges in shelf seas

From Coastal Wiki
Jump to: navigation, search

Introduction

The seabed of shelf seas is generally not flat. In regions where it consists of mobile sediment the seabed is covered with different kinds of structures: ripples, megaripples, dunes (sandwaves), sandbanks and large almost linear sand ridges[1]. Here we focus on the latter kind of seabed structures. According to present insight, large shelf sea sand ridges are not just remnants of relict geological seabed structures. Their development is probably related to the inherent instability of a flat seabed under the action of currents, although in some cases relict seabed structures may have triggered this development.

The first observations of sand ridge fields in shelf seas came as a surprise. Their existence went against intuition: one might expect that such structures tend to be flattened as downslope sand transport at the ridge dominates over upslope transport. This raises questions such as: By which mechanism are these ridges generated and maintained? And what causes the regularity of ridge fields?

Three categories of large linear sand ridges can be distinguished: tidal ridges, shoreface-connected ridges and long bed waves. We discuss the characteristics of these three types of ridges, their occurrence and the way in which they are formed and maintained.


Tidal sand ridges

Characteristics and occurrence

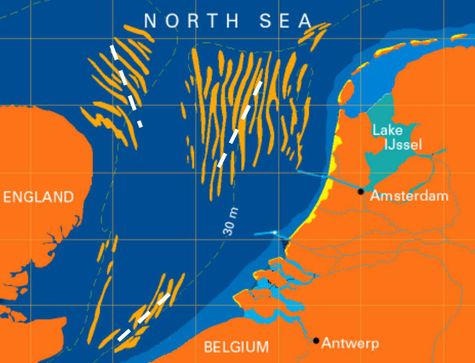Figure 1: Tidal sand ridge fields in the North Sea. The white dashed lines indicate the dominant direction of flood and ebb flow (the tidal flow ellipses are very elongated in these regions). The ridge fields are situated in zones where the depth is between 25 and 40 m and the maximum tidal velocity between 0.6 and 1 m/s. The ridge spacing is typically about 5 km and the ridge height about 10 m. The ridges are rotated cyclonically with respect to the dominant tidal flow direction, with a small angle of 5°-30°. Adapted from Van de Meene[2].
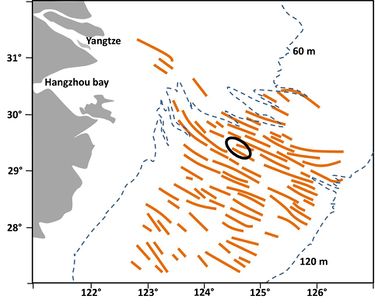Figure 2: Tidal sand ridge field in the East China Sea, situated at depths of 90-100 m. The sand ridge spacing is between 8 and 14 km; the crests are up to several tens of meters high. Maximum tidal currents are in the range 0.5-0.9 m/s and rotary; a typical M2-tidal ellipse is shown in the figure (in black). The tidal ridges probably formed some ten thousand year ago, when sea level was about 70 m lower. However, the sand ridge field is still active and probably adapted to present hydrodynamic conditions. The spacing of the tidal ridges is about twice the spacing in the North Sea for a depth about twice as large, which is consistent with theory. Adapted from [3][4]


Tidal ridges are elongated seabed structures grouped in sand ridge fields. The ridge length generally exceeds 10 km. The mutual ridge spacing (wavelength) is typically 5-10 km. The height of the sand ridges ranges between 5 and 30 m. Tidal sand ridges occur in regions with a sandy bottom, typically at water depths of 30-50 m; they have also been observed in deeper water. Active tidal ridge fields exist in zones where tidal current velocities are larger than 0.5 m/s. Tidal ridge fields generated in the past when sea level was much lower are now usually in a relict regressive state (for example, in the southern Celtic Sea[5]); the tidal ridge field in the East China Sea (figure 2) is an exception. Other active tidal ridge fields have been observed in the southern North Sea (figure 1), in the Yellow Sea [6][7] and at the shelf of North America [8][9].

An indirect observation of the sediment transport pattern around a tidal sand ridge is provided by the behaviour of sand waves (submarine dunes with wavelengths in the order of a few hundred meters, heights up to 20% of the water depth and migration speeds in the order of 10 m per year[10]). The crestline of sand waves is usually perpendicular to the principal tidal current axis. However, in the presence of a tidal sand ridge, the crestlines move in opposite directions along opposite flanks of a tidal ridge, with an anticyclonic rotation of the sand wave crestlines toward the crest of the tidal ridge[11].


Theory: Tidal sand ridge maintenance

Figure 3: Vorticity balance at a tidal sand ridge which is rotated cyclonically with respect to the dominant flood and ebb flow direction. Depth gradients endow the fluid with vorticity, due to frictional torques and Coriolis. (Vorticity is a measure of the degree of rotation; for rotation around a point the vorticity equals twice the angular rotation speed). Flood and ebb carry anticyclonic vorticity to the ridge (1 and 3), both from friction and Coriolis. Flood and ebb take away cyclonic vorticity from the ridge (2 and 4). The net result is creation of anticyclonic vorticity at the ridge, which is equivalent to a residual anticyclonic circulation around the ridge.
Figure 4: The same as in figure 4, now for a ridge which is rotated anticyclonically with respect to the dominant flood and ebb flow directions. In this case the vorticity created by frictional torques is opposite to the vorticity created by Coriolis. The residual circulation around the ridge is therefore smaller than in the case of a cyclonically rotated ridge.
Figure 5: Paths of flood and ebb flow over a tidal sand ridge. Due to inertial delay the flood flow rotates anticyclonically over the ridge. The same holds for the ebb flow.
Figure 6: Sand transport convergence at the tidal ridge crest. Flood and ebb flow (black), residual circulation (blue) and the vector sum (red). The residual circulation is more aligned with the upslope flood and ebb flow (1 and 3) than with the downslope flood and ebb flow (2 and 4). The total upslope velocities are thus larger than the total downslope velocities. The upslope velocities therefore carry more sediment than the downslope velocities, both during flood and ebb. This causes accretion of the ridge crest.

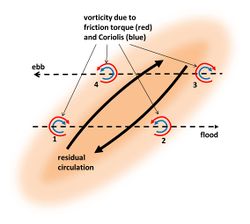
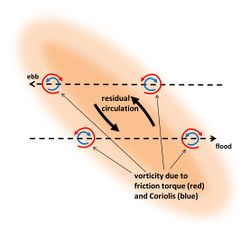
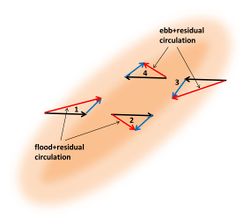
Zimmermann[12] showed that the perturbation of the tidal current by a tidal ridge generates a residual circulation around the ridge, such that upslope flow over the ridge is stronger than downslope flow. This occurs if the ridge crest is not exactly oriented along the unperturbed current direction, but (slightly) rotated. The principle is shown in figures 3 and 4. The existence of a circulation around tidal ridges was already known from hydrographic surveys[13][14]. This circulation is due to increasing bottom friction in upslope direction and decreasing bottom friction in downstream direction, in combination with inertial delay of the response of the tidal current to the frictional torques. The upslope increase of bottom friction deviates the flow in a direction perpendicular to the ridge crest, whereas the downslope decrease of bottom friction restores the initial flow direction. The largest current deviation occurs downstream of the ridge crest, due to inertial response delay (figure 5). The flood and ebb flow deviations are mirror images of each other (assuming rectilinear sinusoidal unperturbed tidal flow). The result is a residual circulation around the ridge crest; the circulation direction is opposite to the direction in which the tidal current is deviated by the ridge. The vector sum of the unperturbed flow and the circulation is larger than the unperturbed flow at the upslope side of the ridge and smaller at the downslope side, both for flood and ebb (see figure 6). This implies that the upslope tidal current carries more sediment than the downslope tidal current. By counterbalancing dissipative downslope transport this mechanism may explain ridge maintenance.

Coriolis acceleration

The asymmetry between upslope and downslope flow is strongest for a small cyclonic angle of the ridge crest relative to the unperturbed flow direction. The stronger asymmetry for cyclonic orientation compared to anticyclonic orientation is related to Coriolis acceleration. Coriolis acceleration counteracts flow deviation in cyclonic direction and reinforces flow deviation in anticyclonic direction. This implies that residual circulation around a cyclonic-oriented tidal ridge is stronger than the circulation around an anticyclonic-oriented tidal ridge, as shown in figures 3 and 4. The mechanism for maintaining a cyclonic-oriented ridge is thus more effective than the mechanism for maintaining an anticyclonic-oriented ridge.

Generation of a tidal sand ridge field

The same mechanism that works for maintaining a tidal ridge field can also initiate such a field starting from a flat bottom. This was first demonstrated by Huthnance[15], who showed that infinitesimal ridge undulations of the seabed can grow exponentially for certain undulation wavelengths. Each ridge undulation that makes an angle with the tidal flow direction generates a residual flow circulation around the crest, which is initially infinitely small. Due to this small circulation the total flow vector is larger toward the crest than away from the crest. The same happens after tidal flow reversal. The net result is an infinitesimal sand transport toward the undulation crest, which is proportional to the crest elevation. The crest therefore grows in proportion to its height, meaning exponential growth. Exponential growth implies that the seabed is unstable to infinitesimal small perturbations (see Stability models). However, the growth rate is not the same for all undulation wavelengths (ridge spacings). For very large wavelengths the inertial delay in flow adaptation is very small; almost no circulation is generated. For very short wavelengths crest growth is counteracted by gravity, favouring downslope transport over upslope transport. Fastest growth occurs for intermediate wavelengths. Huthnance showed that these wavelengths of fastest growth are comparable to the wavelengths (spacings) of tidal sand ridge fields observed in nature. The ridge crests have typically a cyclonic inclination with respect to the tidal flow direction, corresponding to the ridge orientation where the residual flow circulation is strongest due to the Coriolis effect. By performing a linear stability analysis of the coupled hydro-morphodynamic equations in a simple analytic 2D model, Huthnance derived expressions for the preferred spacing and orientation of tidal sand ridges. The fair agreement with observations provides strong support to the above described ridge generation mechanism.

The generation mechanism proposed by Huthnance has been tested since in various numerical models that simulate the tidal current field and sediment transport in far more detail than the simple analytical model. By including wave action, these models are capable to simulate the development of tidal ridges until their final mature stage. It appears that the ridges simulated in these detailed numerical models are very similar to the ridges observed in nature, see de Swart and Yuan (2019) for a review[16].


Shoreface-connected ridges

Figure 7: Bathymetry of the inner shelf slope at the Flemish-Dutch coast, seen from south (bottom) to north (top). The colours indicate depth: red 0-10 m, yellow 10-20 m, green 20-30 m, blue > 30 m. Wind-driven currents are dominantly from south to north. Shoreface-connected ridges are prominent features at the Flemish and southern Dutch coast, with heights of about 10 m and spacing of 5-10 km. Tidal ridges are visible at the left top of the image.
Figure 8: Shoreface-connected ridges at the coast of Long Island, US Atlantic coast. Dominant wind-driven currents are from the north. The ridge spacing is 1-2 km. Image from Nnafie, A.[17].

Characteristics and occurrence

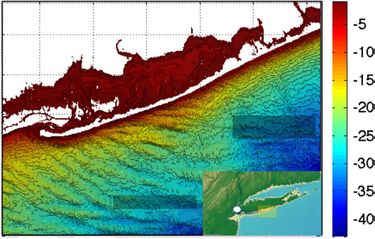
Not all ridge fields in shelf seas have an orientation as predicted by the tidal sand ridge model. This is the case for ridge fields that are observed close to the coast. These sand ridges extend into the nearshore zone with their down-drift tip; they are therefore called shoreface-connected ridges (or shore-oblique ridges). Because of their different orientation, they cannot be generated by the same mechanisms as the tidal sand ridges which are situated further offshore. The updrift offshore tip of shoreface-connected ridges coincides approximately with the break of the inner shelf slope; the ridges are thus situated in the transition zone between shoreface and shelf sea, where the seabed is inclined. They occur typically at storm-dominated coasts, where longshore currents can be strong. The spacing of shoreface-connected ridges is between 1 and 10 km, depending on the field situation. The height is typically 5-10 m. Shoreface-connected ridges have been observed at the Dutch coast (figure 7), the US Atlantic coast[18][19] and the Atlantic coast of South America[20]. Figure 8 shows shoreface-connected ridges at the Long Island coast.

Theory: Generation and maintenance of shoreface-connected ridges

The generation mechanism of shoreface-connected ridges is thought to depend primarily on storm-driven longshore currents, rather than on tidal currents. Trowbridge[21] showed that these ridges can be generated through positive morphodynamic feedback, based on stability analysis of a simplified flow model. The main principles of the mechanism inferred by Trowbridge are summarised in the following and in figures 9 and 10.

Figure 9: Flow path over a shoreface-connected ridge. Dark=land, red=shallow, blue is deep.
Figure 10: Perturbation of frictionless (irrotational) flow over a shoreface-connected ridge with uniform height and width. Dark=land, red=shallow, blue is deep. The fat blue arrows represent undisturbed uniform shore-parallel flow. The small black and red arrows represent flow perturbation at the ridge. The black arrows indicate the increase of the alongshore flow velocity over the ridge, required for continuity of the depth-integrated velocity. With only the black arrows the flow becomes rotational. Conservation of vorticity requires a counter-rotation provided by cross-shore velocity (red arrows). The flow perturbation is larger at the onshore flank of the ridge than at the offshore flank, because of the larger depth offshore. The cross-ridge flow is thus decelerating at the ridge crest. The same holds for offshore sand transport. Hence, the ridge crest will accrete.

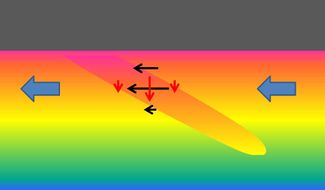
Assuming an initial small seabed perturbation in the form of a ridge with a down-drift shoreward rotation, a longshore current is deviated in offshore direction when crossing the ridge (figure 9). This deviation is mainly due to flow continuity and vorticity conservation, rather than to frictional torques (initially the perturbation slope is smaller than the inner-shelf slope; bed friction therefore does not increase when the current is deflected in offshore direction over the ridge). The magnitude and angle of the velocity perturbation depends on the relative depth change when crossing the ridge. The flow perturbation is thus stronger at the shallow coast-oriented inner flank of the ridge than at the deeper offshore-oriented outer flank. The velocity is thus decreasing when the flow crosses the ridge crest. The same holds for sand transport at the ridge crest. The decrease of sand transport along the flow path implies sand deposition at the ridge crest. By this mechanism a shoreface-connected ridge can be generated initially on a flat inclined seabed and a mature shoreface-connected ridge can be maintained against the dispersive action of waves and gravity. According to this theory, shoreface-connected ridges should always be oriented with the down-drift tip turned toward the coast. All observed shoreface-connected ridges in nature conform to this orientation. Trowbridge derived from his model estimates of the preferred spacing and orientation of shoreface-connected ridges. His results are in fair agreement with observations and hence provide strong support for the generation and maintenance mechanisms of shoreface-connected ridges described above.


Long bed waves

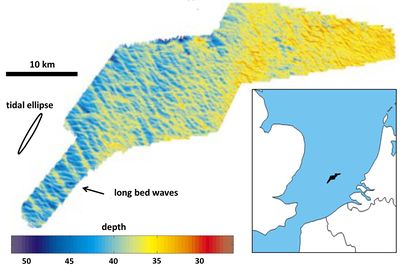
Figure 11: Multibeam record of seabed bathymetry in a small area of the southern North Sea; the location is indicated in the map at the right. Long bed waves with a spacing of 1.6 km are clearly visible, especially in the southwestern part. The crests are oriented ~ 60° counter-clockwise relative to the main axis of the tidal ellipse. The smaller seabed structures visible in the image are dunes (sandwaves). The depth difference between the western and eastern parts of the area is due to the presence of a tidal ridge. Adapted from [22]

Analysis of recent multibeam seabed surveys in the North Sea by Knaapen et al. revealed the presence of long bed waves: regularly spaced sand ridges with a wavelength of 1-2 km [22][23], see figure 11. These bed forms are probably linked to oscillatory tidal currents, like tidal sand ridges, but they are less prominent. The coastal area where long bed waves were detected is characterised by rotating tidal currents (wide tidal current ellipse) with maximum velocity of the order of 0.6 m/s. The typical grain size is equal to about 0.4 mm and the average water depth is 40 m. The crests of long bed waves are oriented either clockwise (angle ~ 30°) or counter-clockwise (angle ~ 60°) with respect to the direction of the dominant tidal current. It is unclear why the crests of counter-clockwise oriented long bed waves are rotated further than the crests of tidal sand ridges. Blondeaux et al. [24] presented theoretical evidence that long bed waves only form if tidal currents are elliptical and the maximum tidal flow velocity is just above the threshold value for the initiation of sediment motion.


Related articles

Stability models
Coriolis acceleration
Tidal motion in shelf seas


References

  1. ↑ Dronkers, J. (2016) Dynamics of Coastal Systems 2nd edition. World Scientific Publ. Co.
  2. ↑ Van de Meene, J.W.H. (1994) The shoreface-connected ridges along the central Dutch coast. PhD thesis, University Utrecht
  3. ↑ Liu, Z., Berné, S., Saito, Y., Yu, H., Trentesaux, A., Uehara, K., Yin, P., Liu, P., Li, C., Hu, G. and Wang, X. (2013) Internal architecture and mobility of tidal sand ridges in the East China Sea. Cont. Shelf Res. 27: 1820-1834
  4. ↑ Shen, Z., Wu, X., Fei, Y., Xu, X. and Chen, X. (2013) Surface tidal currents in the open sea area to the east of the Zhoushan Islands measured with high frequency surface wave radar. Acta Oceanol. Sin. 32: 5-10
  5. ↑ Berné, S., Lericolais, G., Marsset, T., Bourillet, J.F. and De Batist, M. (1998) Erosional offshore sand ridges and lowstand shorefaces: examples from tide- and wave-dominated environments in France. J. Sed. Res. 68: 540-555
  6. ↑ Liu, Z., Huang, Y. and Zhang, Q. 1989. Tidal current ridges in the southwestern Yellow Sea. J. Sed. Petr. 59: 432-437
  7. ↑ Xu, F., Tao, J., Zhou, Z., Coco, G. and Zhang, C. (2016) Mechanisms underlying the regional morphological differences between the northern and southern radial sand ridges along the Jiangsu Coast, China. Mar. Geol. 371: 1-17
  8. ↑ Swift, D.J.P., Duane, D.B. and McKinney, T.F. (1973) Ridge and swale topography of the middle Atlantic Bight, North America: secular response to the Holocene hydraulic regime. Marine Geology 15: 227-247
  9. ↑ Davis, R.A., Klay, J. and Jewell, P. (1993) Sedimentology and Stratigraphy of Tidal Sand Ridges Southwest Florida Inner Shelf. J. Sedimentary Petrology 63: 91-104
  10. ↑ Hulscher, S.J.M.H. and van den Brink, G.M. (2001) Comparison between predicted and observed sand waves and sand banks in the North Sea. J. Geophysical Research 106: 9327-9338
  11. ↑ Leenders, S., Damveld, J.H., Schouten, J., Hoekstra, R., Roetert, T.J. and Borsje, B.W. (2021) Numerical modelling of the migration direction of tidal sand waves over sand banks. Coastal Engineering 163, 103790
  12. ↑ Zimmerman, J.T.F. 1978. Topographic generation of residual circulation by oscillatory (tidal) currents. Geophys. Astrophys. Fluid Dyn. 11: 35-47
  13. ↑ Robinson, A.H.W. 1965. Residual currents in relation to shoreline evolution of the east Anglian coast. Mar.Geol. 4: 57-84
  14. ↑ McCave, I.N. and Langhorne, D.N. 1982. Sand waves and sediment transport around the end of a tidal sand bank. Sedimentology 29: 95-110
  15. ↑ Huthnance, J.M. 1982. On one mechanism forming linear sandbanks. Est. Coast. Mar. Sci. 14: 79-99
  16. ↑ De Swart, H.E. and Yuan, B. 2019. Dynamics of offshore tidal sand ridges, a review. Environmental Fluid Mechanics 19: 1047–1071 (open access)
  17. ↑ Nnafie, A. 2014. Formation and long-term evolution of shoreface-connected sand ridges: modeling the effects of sand extraction and sea level rise. PhD thesis, Utrecht University
  18. ↑ Swift, D.J.P., Parker, G., Lanfredi, N.W.,Perillo, G. and Figge, K. (1978) Shoreline-connected sand ridges on American and European shelves - a comparison. Est. Coast. Mar. Sci. 7: 227-247
  19. ↑ Figueiredo, A.G., Swift, D.J.P., Stubblefield, W.L. and Clarke, T.L. (1981) Sand ridges on the inner Atlantic shelf of North America: morphometric comparisons with Huthnance stability model. Geomarine Letters 1: 187-191
  20. ↑ Parker, G., Lanfredi, N.W. and Swift, D.J.P. (1982) Seafloor response to flow in a southern hemisphere sand ridge field: Argentine inner shelf. Sed. Geol.33: 195-216
  21. ↑ Trowbridge, J.H. (1995) A mechanism for the formation and maintenance of the shore-oblique sand ridges on storm-dominated shelves. J. Geophys. Res. 100: 16071-16086
  22. ↑ 22.0 22.1 Knaapen, M. A., Hulscher, S., Vriend, H. J. and Stolk, A. (2001) A new type of sea bed waves. Geophys. Res. Letters 28: 1323-1326
  23. ↑ Van Dijk, T. A. G. P., Lindenbergh, R. C. and Egberts, P. J. P. (2008) Separating bathymetric data representing multiscale rhythmic bed forms: A geostatistical and spectral method compared, J. Geophys. Res. 113, F04017, doi:10.1029/2007JF000950
  24. ↑ Blondeaux, P., De Swart, H. E. and Vittori, G. (2009) Long bed waves in tidal seas: an idealized model. J. Fluid Mech. 636: 485-495


The main author of this article is Job Dronkers
Please note that others may also have edited the contents of this article.
Citation: Job Dronkers (2024): Sand ridges in shelf seas. Available from http://www.coastalwiki.org/wiki/Sand_ridges_in_shelf_seas [accessed on 21-12-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Sand_ridges_in_shelf_seas&oldid=81214"