Data interpolation with Kriging

Introduction: Rationale of the kriging approach

Environmental features, such as coastal bathymetry or seabed composition, are the product of many interacting geophysical processes. These processes are in principle deterministic, but their interactions are so complex that the variation seems random. This complexity and incomplete knowledge of the processes means that a deterministic or mathematical solution to quantify the variation is out of reach. Statistical methods may therefore be used to describe these characteristics..

Suppose one has to predict the value of a variable from experimental data in a location where no measurements are available, knowing that the underlying process has a significant random component. A common procedure is to fit an a priori chosen parameterized function to the data by minimizing the sum of squared deviations, the so-called ordinary least squares method (OLS). However, this method has a number of shortcomings. It does not provide the best possible estimate due to the arbitrariness of the chosen interpolation function. OLS does not give the true uncertainty of the prediction; an estimate based on the squared residuals is always significantly smaller than the real uncertainty. OLS does not take into account any correlations between the data. In cases where the measurement locations are not uniformly distributed around the target location, OLS will generally overweight data clusters compared to isolated data closer to the prediction location. The latter deficiency can be mitigated by linear regression using generalized least squares (GLS).

Kriging is a method to overcome the shortcomings of the least-square methods. It is basically a linear regression method for estimating point values (or spatial averages) at any location of a region. The concept was developed by D. Krige (1951) and the theoretical foundation was given by G. Matheron (1969). Kriging refers to a group of geostatistical interpolation methods in which the value at an unobserved location [math]\vec{x_0}[/math] is predicted by a linear combination of the measured values [math]z_i[/math] at surrounding locations [math]\vec{x_i}, \; i=1, .. n[/math], using weights [math]w_i[/math] according to a model that takes into account spatial correlations between the data. Kriging provides unbiased estimates with minimum variance.

In the following we present the basics of the theory underlying kriging following Goovaerts (1997).

Kriging principles

Observations provide a set of data [math]z_i \equiv z(\vec{x_i}), \; i=1, .., n[/math] in spatial locations [math]\vec{x_i}[/math], which are considered to be a particular realization of a process [math]Z[/math] with a significant random component. Measuring locations [math]\vec{x_i}, \; i=1, .. n[/math] are selected in a close neighborhood of a target location [math]\vec{x_0}[/math] where we want to predict the value of [math]Z[/math]. The random component [math]\epsilon(\vec{x})[/math] of the observations represents the result of unobserved small-scale processes and observation errors.

The variable [math]Z(\vec{x_i})[/math] representing the random process is characterized by a smoothly varying deterministic component [math]m[/math] and a stochastic component [math]\epsilon[/math],

[math]Z(\vec{x})=m(\vec{x})+\epsilon(\vec{x}), \qquad (1)[/math]

with [math]E[Z(\vec{x})]=m(\vec{x}), \; E[\epsilon(\vec{x})]=0 , \;[/math] where [math]E[f][/math] designates the statistical expected value of the random function [math]f[/math].

The estimator [math]Z^*[/math] of [math]Z[/math] at location [math]\vec{x_0}[/math] is constructed as a weighted sum of the values of [math]Z[/math] at the observed neighborhood locations [math]\vec{x_i}, i=1, .. ,n [/math]:

[math]Z^*(\vec{x_0}) = \sum_{i=1}^{n} w_i Z_i = m_0 + \epsilon (\vec{x_0}) = m_0 + \sum_{i=1}^{n} w_i \big( Z_i - m_i \big) , \qquad (2)[/math]

where [math]Z_i \equiv Z(\vec{x_i}), \; m_0 \equiv m(\vec{x_0}), \; m_i \equiv m(\vec{x_i}) = E[Z(\vec{x_i})][/math] and [math]w_i \equiv w_i(\vec{x_0})[/math] for [math]i=1, .. ,n[/math].

The predictor [math]Z^*[/math] is unbiased, because [math]E[Z^*(\vec{x_0})]=m_0 =E[Z(\vec{x_0})] .[/math]

The kriging estimator (2) can also be written [math]Z^*(\vec{x_0}) = \sum_{i=1}^{n} w_i Z_i + m_0 - \sum_{i=1}^{n} w_i m_i , \quad[/math] showing that

[math]\quad m_0 - \sum_{i=1}^{n} w_i m_i = 0 . \qquad (3) [/math]

The basic principles of the kriging method can be summarized as follows:

• ASSUMPTION A: the spatial distribution of the variable [math]Z(\vec{x})[/math] has small-scale fluctuations [math]\epsilon(\vec{x})[/math] that are not well captured by the observation grid [math]\vec{x_i}[/math];
• ASSUMPTION B: the fluctuations [math]\epsilon_i \equiv \epsilon(\vec{x_i})[/math] at the observation points [math]\vec{x_i}[/math] can be considered as representing a stochastic process which is approximately Gaussian-distributed with zero mean;
• ASSUMPTION C: the fluctuations [math]\epsilon_i[/math] at neighboring observation points are significantly correlated;
• ASSUMPTION D of translation/rotation invariance: the covariances [math]C(r_{ij}) \equiv E[\epsilon_i \epsilon_j][/math] depend only on the distances [math]r_{ij} \equiv |\vec{x_i} - \vec{x_j}|[/math] for [math]i,j=0,1, .., n[/math];
• METHOD: the estimator [math]Z^*(\vec{x_0})[/math] for interpolation at an intermediate location [math]\vec{x_0}[/math] is given by the weighted sum of the values of the variable [math]Z(\vec{x})[/math] at neighboring observation points [math]\vec{x_i}[/math], where the weights [math]w_i \equiv w_i(\vec{x_0})[/math] are determined by requiring that the squared error [math]\sigma_0^2 \equiv E \Big[ \big( Z^*(\vec{x_0}) - Z(\vec{x_0}) \big)^2 \Big][/math] is minimal, taking into account the condition (3).

The METHOD implies

[math]\Large\frac{\partial \sigma_0^2}{\partial w_i}\normalsize = 0, \; i=1, .., n ,\qquad (4) [/math]

where the partial derivates are subject to the condition (3).

Ordinary Kriging (OK)

In ordinary kriging (OK) it is assumed that there are sufficient data locations [math]\vec{x_i}[/math] close to [math]\vec{x_0}[/math] that it is possible to choose a neighborhood in which [math]m(\vec{x})[/math] is approximately constant,

[math]E[Z_i] \equiv m_i \approx m(\vec{x_0}) \equiv m . \qquad (5)[/math]

The predictor [math]Z^*[/math] is written as:

[math]Z^*(\vec{x_0}) = m + \sum_{i=1}^n w_i (Z_i -m) = \sum_{i=1}^n w_i Z_i + m \big(1 - \sum_{i=1}^n w_i \big). \qquad (6)[/math]

Because [math]Z^*(\vec{x_0}) = \sum_{i=1}^n w_i Z_i , \quad [/math] we have

[math]\sum_{i=1}^n w_i - 1 = 0 . \qquad (7)[/math]

The coefficients [math]w_i[/math] can be determined from this equation and from the condition (4), taking into account the constraint Eq. (7). This system of [math]n+1[/math] equations is solved by introducing Eq. (7) in Eq. (4) with a so-called Lagrange multiplier [math]\mu[/math]. The Lagrange multiplier is an additional unknown constant which makes the number of unknown parameters equal to the number of equations.

The system of linear equations from which [math]w_i[/math] and [math]\mu[/math] must be solved is given by

[math]\phi=\sigma_0^2 + 2 \mu \big(\sum_{i=1}^n w_i – 1 \big) , \quad \Large\frac{\partial \phi}{\partial \mu}\normalsize = 0, \; \Large\frac{\partial \phi}{\partial w_i}\normalsize = 0, \; i=1, .., n\qquad (8). [/math]

The partial derivatives of condition (8) yield Eq. (7) and a system of [math]n[/math] linear equations (see Appendix A):

[math]\sum_{j=1}^n \gamma_{ij} w_j - \mu = \gamma_{i0} , \; i=1, .., n , \qquad (9)[/math]

where the semivariances [math]\gamma_{ij}, \gamma_{i0}[/math] are defined by

[math]\gamma_{ij} \equiv \gamma(r_{ij}) \equiv ½ E[(\epsilon_i-\epsilon_j)^2] = ½ E[(Z_i-Z_j)^2]; \; \gamma_{i0} \equiv \gamma(r_{i0}) ; \quad r_{ij}=|\vec{x_i}-\vec{x_j}| ; \; r_{i0} = |\vec{x_i}-\vec{x_0}| , \qquad (10)[/math]

and where [math]\mu[/math] is a parameter to be determined from the [math]n+1[/math] equations (7) and (9).

Solution by means of a variogram

Fig. 1. Example of a variogram.

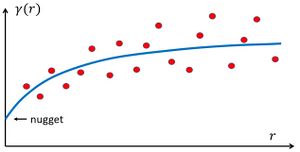
For solving the equations (9) the variograms [math]\gamma_{ij}, \gamma_{i0}[/math] must be known. An approximate estimate of the variograms can be obtained if translation invariance is assumed (i.e., the variograms depend for the particular chosen neighborhood only on the distances [math]r_{ij}=|\vec{x_i}-\vec{x_j}|, \; r_{i0} = |\vec{x_i}-\vec{x_0}|[/math]) and if the chosen neighborhood contains a sufficient number [math]n[/math] of data points. In this case the function [math]\gamma(r)[/math] (the variogram) can be constructed from the [math]½n(n-1)[/math] data values [math] ½ (z_i-z_j)^2, \; i,j=1, .., n, i \ne j[/math], each corresponding to a particular value [math]r=r_{ij}[/math]. An explanation is given in appendix B and a typical example is shown in Fig. 1. The variogram generally appears as a plot with data points scattered around a curve, which can be represented by a smooth function. Different parameterized functions can be tried out. According to the pattern of data points, the most suited function should be chosen and fitted to the variogram. Once the variogram function [math]\gamma(r)[/math] has been determined, the weights [math]w_i[/math] can be found from the system of [math]n+1[/math] linear equations (7, 9). The value of the random process [math]Z[/math] at location [math]x_0[/math] can then be determined from

[math]Z^*(\vec{x_0}) = \sum_{i=1}^n w_i z_i . \qquad (11)[/math]

The error is given by (see appendix A)

[math] \sigma_0^2 = \mu + \sum_{i=1}^n w_i \gamma_{i0}. \qquad (12)[/math]

Kriging the mean

The mean [math]m[/math] can be determined in a way similar to the kriging procedure for the stochastic component. The estimator of the mean is given by

[math]m^*=\sum_{i=1}^n u_i Z_i . \qquad (13)[/math]

The conditions [math]E[m^*] = E[m][/math] and [math]E[Z_i]=m[/math] imply [math]\sum_{i=1}^n u_i=1 . \qquad (14)[/math]

The mean has no stochastic component: [math]E[m^*m]=E[m^2]=m^2 .[/math]

The squared error is thus given by [math]\sigma_m^2=E[(m^*-m)^2]=\ \sum_{i,j=1}^n u_i u_j C_{ij} , \qquad (15)[/math]

where [math]C_{ij}[/math] are the covariances [math]C_{ij} \equiv C(r_{ij}) \equiv E[(Z_i-m)(Z_j-m)][/math].

Minimizing the error taking into account the condition (13) is done as for the stochastic component

[math]\phi=\sigma_m^2 + 2 \mu \big(\sum_{i=1}^n u_i – 1 \big) , \quad \Large\frac{\partial \phi}{\partial \mu}\normalsize = 0, \; \Large\frac{\partial \phi}{\partial u_i}\normalsize = 0, \; i=1, .., n\qquad (16). [/math]

The condition (16) yields together with Eq. (13) a system of [math]n+1[/math] linear equations

[math]\sum_{j=1}^n C_{ij} u_j + \mu = 0 , \; i=1, .., n , \qquad (17)[/math]

from which the coefficients [math]u_i[/math] and the Lagrange multiplier [math]\mu[/math] can be determined. The mean can now be computed from the data [math]z_i[/math]:

[math]m^* = \sum_{i-1}^n u_i z_i . \qquad (18)[/math]

Kriging in the presence of trends

The minimum observation area required for data interpolation to a target location can be too large to ignore trends. The ordinary kriging (OK) method cannot be applied in this case. Removing the trend by subtracting from the data a fitted function based on least-squares will generally introduce a bias as explained in the introduction and does not provide a correct error estimate.

The trend [math]m(\vec{x})[/math] can be determined by a kriging procedure similar to the procedure for the mean. Therefore it is assumed that an estimator of the trend [math]m^*[/math] can be written as a linear superposition of known functions [math]f_k(\vec{x}), \; k=1, .., K[/math],

[math]m^*(\vec{x})=\sum_{k=1}^K a_k f_k(\vec{x}) . \qquad (19)[/math]

For example, in case of a linear trend one may choose [math]f_1=1, f_2=x, f_3=y[/math].

The estimator of the process [math]Z[/math] at the target location [math]\vec{x_0}[/math] can now be written as:

[math]Z^*(\vec{x_0}) = \sum_{i=1}^n w_i Z_i = m^*(\vec{x_0}) + \sum_{i=1}^n w_i \big( Z_i - m^*(\vec{x_i}) \big) = \sum_{i=1}^n w_i Z_i + \sum_{k=1}^K a_k \Big(f_{0k} - \sum_{i=1}^n w_i f_{ik} \Big) , \qquad (20)[/math]

where [math]f_{0k}=f_k(\vec{x_0}), f_{ik}=f_k(\vec{x_i})[/math].

The condition [math]E[Z^*(\vec{x_i})] = E[Z(\vec{x_i})] = m^*(\vec{x_i})[/math] yields [math]K+1[/math] equations [math] f_{0k} - \sum_{i=1}^n w_i f_{ik} = 0 , \quad \sum_{i=1}^n w_i - 1 =0 . \qquad (21)[/math]

The squared error [math]\sigma^2[/math] is the same as for ordinary kriging, [math]\sigma^2=\sigma_0^2[/math] (Eq. (A1)).

The function to be minimized requires [math]K+1[/math] Lagrange multipliers [math]\mu_k[/math] in order to account for the conditions (21),

[math]\phi=\sigma_0^2+ 2\mu_0 \Big(\sum_{i=1}^n w_i - 1\Big) + 2\sum_{k=1}^K \mu_k \Big(\sum_{i=1}^n w_i f_{ik} - f_{0k} \Big) . \qquad (22)[/math].

Minimization with respect to [math]w_i, i=1, .., n[/math] and [math]\mu_k, k=0, 1, .., K[/math] yields the system of [math]K+1[/math] linear equations (21) and [math]n[/math] linear equations

[math]\sum_{i=1}^n w_i \gamma_{ij} - \mu_0 - \sum_{k=1}^K \mu_k f_{ik} = \gamma_{i0} , \qquad (23)[/math]

from which the parameters [math]w_i, \mu_k[/math] can be determined if the variogram function [math]\gamma(r)[/math] is known. However, the semivariances [math]\gamma_{ij} \equiv ½ E[(\epsilon_i-\epsilon_j)^2][/math] cannot be estimated directly from the data because the trend components [math]m_i[/math] are not yet known. This issue can be solved by using an iterative procedure.

Another procedure to remove the trend from the data makes use of regression analysis with generalized least squares (GLS). However, the estimation of the residuals by generalized least squares is also an iterative process: first the drift model is estimated using ordinary least squares (OLS); then the covariance function of the residuals is used to obtain the GLS coefficients; these can be used to re-compute residuals and so on.

Applications and limitations

Many environmental parameters are influenced by processes that interact at a wide range of spatial scales. Spatial surveys generally do not resolve the smallest scales, where subscale processes produce correlations between values observed in a wider neighborhood. In such cases, kriging is the most appropriate technique to determine parameter values at intermediate unobserved locations and to estimate the uncertainty of the interpolated values. Examples in the coastal and marine environment include data collected for bathymetric mapping, sediment maps, mapping of benthic communities, plankton distributions, seabed geochemical components, pollutants and mineral resources.

Several commercial and free GIS software packages can perform kriging interpolation. However, the user must be aware that the kriging procedure is highly sensitive to the specification of the correlation and variance functions inferred from the data. Mis-specification of the variogram model leads to erroneous weights of the kriging interpolator and inaccurate interpolations. Translational invariance of the correlations is a crucial assumption underlying the kriging method. Whether this assumption is met must be verified experimentally and/or theoretically. So some other methods (e.g. Bayesian approaches) have been developed if the kriging conditions are not well satisfied. In general, the accuracy of interpolation by kriging will be limited if the number of observations sampled is small, the data has limited spatial scope, or the data is in fact not sufficiently spatially correlated. In these cases, a sample variogram is hard to generate, and other methods (e.g. regression) may prove preferable to kriging for spatial prediction.

Appendix A

The error [math]\sigma_0^2[/math] can be written

[math]\sigma_0^2 \equiv E \Big[ \big( Z^*(\vec{x_0}) - Z(\vec{x_0}) \big)^2 \Big] = E \Big[ \big( \sum_{i=1}^n w_i (m+\epsilon_i) - m - \epsilon_0 \big)^2 \Big] = E \Big[ \big( \sum_{i=1}^n w_i \epsilon_i - \epsilon_0 \big)^2 \Big] = \sum_{i,j=1}^n w_i w_j C_{ij} + C(0) -2 \sum_{i=1}^n w_i C_{i0} \; , \qquad (A1)[/math]

where the covariances [math]C_{ij} \equiv C(r_{ij}) \equiv E[\epsilon_i \epsilon_j] \equiv E[(Z_i-m) (Z_j-m)] , \; C_{i0} \equiv C(r_{i0}) \equiv E[\epsilon_i \epsilon_0] , \; C(0)=E[\epsilon_i^2]=E[\epsilon_0^2][/math] and [math] r_{ij}=|\vec{x_i}-\vec{x_j}|, \; r_{i0}=|\vec{x_i}-\vec{x_0}| . [/math]

The condition (8) then yields

[math]\Large\frac{\partial \phi}{\partial w_i}\normalsize = 2 \Big( \mu + \sum_{j=1}^n w_j C_{ij} - C_{i0} \Big) = 0 , \; i=1, .., n . \qquad (A2)[/math]

Instead of the covariance it is often more practical to consider the variance. The semivariances [math]\gamma_{ij}, \gamma_{i0}[/math] are defined by [math]\gamma_{ij} \equiv \gamma(r_{ij}) \equiv ½ E[(Z_i-Z_j)^2][/math], [math]\gamma_{i0} \equiv \gamma(r_{i0})[/math].

Because [math]2 \gamma_{ij} \equiv E[(Z_i-Z_j)^2] = E[(Z_i-m)^2]+E[(Z_j-m)^2] – 2 E[(Z_i-m)( Z_j-m)] = 2 C(0) – 2 C_{ij}[/math], we have

[math]C_{ij} = C(0) - \gamma_{ij} . \qquad (A3)[/math]

Substitution in Eq. (A2) yields Eq. (9),

[math]\sum_{j=1}^n \gamma_{ij} w_j - \mu = \gamma_{i0} , \; i=1, .., n , \qquad (9)[/math]

Substitution of (A3) in the expression (A1) gives

[math]\sigma_0^2 = \sum_{i,j=1}^n w_i w_j C_{ij} + C(0) -2 \sum_{i=1}^n w_i C_{i0} = -\sum_{i,j=1}^n w_i w_j \gamma_{ij} +2 \sum_{i=1}^n w_i \gamma_{i0} . \qquad (A4)[/math]

The value of [math]\mu[/math] can be found by multiplying Eq. (A2) by [math]w_i[/math] and by summing over [math]i[/math]. From comparison with the expression (A4) we find

[math]\sigma_0^2 = \mu + \sum_{i=1}^n w_i \gamma_{i0} . \qquad (A5)[/math]

Appendix B

The variogram function [math]\gamma(r)[/math] is related to the covariance function [math]C(r)[/math] by (A3),

[math]\gamma(r)=C(0)-C(r) . \qquad (B1)[/math]

The practical way to establish the variogram is by taking the average of all data pairs [math]\vec{x_i}, \vec{x_j}[/math] lying in a strip of width [math]\Delta r[/math] at a distance [math]r[/math] from each other. The variogram is computed as

[math]\gamma(r)=\Large\frac{1}{2 n_r}\normalsize \sum_{i,j, i \ne j} (z_i – z_j)^2 , \qquad (B2)[/math]

for the [math]n_r[/math] data locations satisfying [math]r \lt |\vec{x_i} - \vec{x_j}|\lt r+\Delta r[/math]. The values of [math]\gamma(r)[/math] computed in this way are plotted as in Fig. 1.

The strongest correlation is expected at short distances [math]r[/math]. However, if one extrapolates the variance [math]\gamma(r)[/math] to small values of [math]r[/math], the result will generally not vanish. This can be due to measurement errors, to temporal fluctuations in case of non-simultaneous observations or to processes at smaller scales than the observation grid. The result [math]\gamma(0)[/math] is called the nugget, see Fig. 1. The correlation weakens at large distances, so the variance increases. The kriging method is meaningful only if the variance becomes substantially larger than the nugget. The variance may level off at great distance to some value close to [math]C(0)[/math]. However, it may also increase further. In that case there can be a trend in the data that falsifies the assumption of uniform [math]m(\vec{x})[/math] that underlies the ordinary kriging model. If the number of datapoints in a neighborhood where [math]m(\vec{x})[/math] is approximately uniform is too small for constructing a variogram, a procedure must be chosen for incorporating trend analysis into the kriging method, see Kriging in the presence of trends.

Kriging is a local predictor, and only the nearest few points to the interpolation point carry significant weight, especially if the nugget variance is a small proportion of the total variance. As a rule of thumb, the minimum number of datapoints in the neighborhood of uniform [math]m(\vec{x})[/math] for applying ordinary kriging should be larger than 10.

Outliers and skewness of the dataset can introduce bias into the variogram. Assumption B regards the Gaussian distribution of the random component of the random process. Strong skewness can often be reduced by log-transformation of the data. In this case the kriging method is applied to the log-transformed dataset. Outliers due to measurement errors or other causes should be removed from the dataset. A bias in the variogram can also result from anisotropy of the random process. If the variance along one axis is very different from the variance along the perpendicular axis, the effect of anisotropy can be overcome by a linear transformation (contraction or dilation) of one of the axes.

A well-chosen representation of the variogram is essential for the quality of the kriging interpolation. This can be checked through the MSRD (mean squared deviation ratio) criterion for the mean of the squared errors divided by the corresponding kriging variances. Ideally the MRSD should equal 1, and so for kriging one should choose the variogram model for which the MSDR is closest to 1.

Related articles

Interpolation of measured grain-size fractions

Acoustic kelp bed mapping in shallow rocky coasts - case study Helgoland (North Sea)

Interpolation of remote sensing images

External links

https://gisgeography.com/kriging-interpolation-prediction/

https://desktop.arcgis.com/en/arcmap/10.3/tools/3d-analyst-toolbox/how-kriging-works.htm

References

The main author of this article is Job Dronkers Please note that others may also have edited the contents of this article. Citation: Job Dronkers (2024): Data interpolation with Kriging. Available from http://www.coastalwiki.org/wiki/Data_interpolation_with_Kriging [accessed on 21-12-2024] For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Dronkers J