Floating breakwaters

From Coastal Wiki
Jump to: navigation, search

Use of floating breakwaters

Fig. 1. Example of floating box-breakwater (Fezzano,SP-Italy; courtesy of INGEMAR srl)

Use of floating breakwaters

Floating breakwaters attenuate waves by reflecting and dissipating part of the incident wave energy. Unlike overtopped fixed breakwaters, they do not introduce surplus water into the sheltered area. Floating breakwaters are commonly used as piers in marinas and as protective structures for marinas and small-craft basins in semi-sheltered waters. They are especially suited to areas with a large tidal range, because they follow the water level. Floating breakwaters are seldom used as shoreline protection structures because they are generally unsuitable for exposed open-sea conditions.

Floating breakwaters can provide a relatively economical alternative to conventional fixed breakwaters in mild wave climates, typically with significant wave heights not much greater than 1 m and wave periods of about 4 s or less[1]. Conditions that may favor the use of floating breakwaters include[2]:

  1. Poor foundation conditions: Floating breakwaters may be suitable where weak seabed conditions make bottom-supported breakwaters difficult or expensive to construct.
  2. Deep water: In water depths greater than about 6 m, bottom-founded breakwaters are often more expensive than floating alternatives.
  3. Water quality: Floating breakwaters generally cause less obstruction to water exchange and fish migration than fixed emerged breakwaters.
  4. Ice problems: Floating breakwaters can be removed or towed to protected areas if ice formation is a problem. They may therefore be suitable for seasonal mooring areas.
  5. Visual impact: Floating breakwaters have a low profile and cause limited visual intrusion, especially in areas with large tidal ranges.
  6. Flexible layout: Floating breakwaters can often be rearranged or relocated with relatively limited effort.

Floating breakwaters also have other advantages compared with breakwaters built on the seabed. They usually cause less downdrift erosion than emerged breakwaters and, unlike submerged breakwaters, they do not generate strong rip currents or substantial wave-induced water-level setup against the shore. Because they are transportable, they can also provide temporary wave shelter for mangrove restoration. Mangrove seedlings may need protection for several years before they can withstand the natural wave climate. Once a new mangrove fringe has become established, further seaward expansion of the mangrove belt can be promoted by moving the floating breakwater to a new suitable location.[3] Despite these advantages, floating breakwaters can still produce negative environmental effects, for example through anchoring, shading, debris accumulation, material degradation, maintenance activities and altered local sedimentation.


Floating breakwaters work by dissipating and reflecting part of the wave energy. No surplus water is brought into the sheltered area by wave overtopping. Floating breakwaters are normally used as piers in marinas, but also as protective structures for marinas in semi-protected areas. They are especially suited for areas where the tidal range is high, as they follow the water level. Floating breakwaters are seldom used as shoreline protection structures because they are not suitable for installation in the open sea.


Types of floating breakwaters

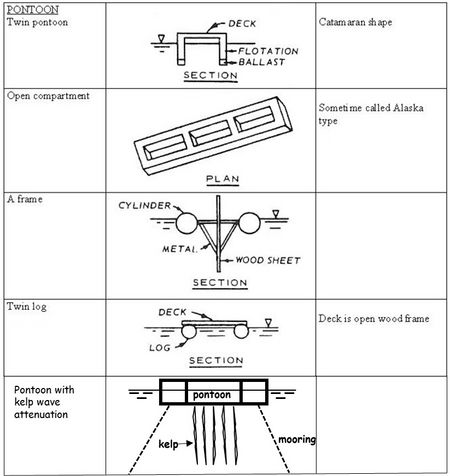
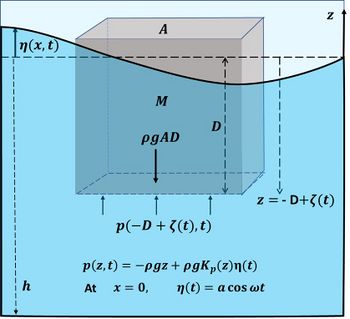
Floating breakwaters are commonly divided into four general categories[2]:

  1. Box
  2. Pontoon
  3. Mat
  4. Tethered float.

For each category, some types of floating breakwaters are shown in figures 2 - 5. The first three types have been more widely investigated by means of physical models and prototype experience than the last one.

Floating breakwaters often consist of several interconnected modules. Connections may be flexible, allowing mainly relative roll about the breakwater axis, or pre- or post-tensioned so that the modules behave more nearly as a single unit. In the latter case the efficiency is higher, but the forces between modules are higher. The modular assemblage and the mooring system (including position of connections) are primary points of concern for this kind of structures. The wave-induced forces on the connections increase with peak wave period and obliquity; intermediate connections withstand much higher forces than terminal connections[4].

The performance of a floating breakwater depends on the strongly non-linear interaction of the incident wave (that may partially overtop the module and is in general short-crested and oblique) with the structure dynamics. The forces induced by the mooring system and the connections between the modules complicate the interactions. Accurate design is necessarily based on the combination of numerical and physical models[5].

Large breakwaters are frequently built with used barges, ballasted to the desired draft with sand or rock.

Floating breakwaters are most effective for wave damping when their width [math]W[/math] is of order of half the wavelength [math]L[/math] or larger. The net forces on the mooring and anchoring system are also substantially less for such large widths, because different parts of the structure are subjected to opposite wave forces[1].

The natural period of oscillation of a floating breakwater is of the order of [math]\; T \sim 2 \, \pi \, \sqrt{\large\frac{M}{\rho g A}\normalsize} \;[/math], where [math]\rho=[/math] seawater density, [math]g=[/math] gravitational acceleration, [math]A=[/math] horizontal section of the breakwater, and [math]M=[/math] breakwater mass. However, in real floating-breakwater design, added mass and mooring stiffness can appreciably alter the natural periods. The natural periods of the relevant motion modes should be sufficiently separated from the energetic wave periods to avoid resonance and excessive motions. These requirements imply that floating breakwaters are not suited in areas with long-period high waves. A simple analytical analysis is presented in the Appendix.

Box breakwaters

Box type breakwaters are used most frequently (see figures 1 and 2). Most box-type breakwaters have been constructed of reinforced concrete modules. Reinforced concrete modules are either empty inside or, more frequently, have a core of light material (e.g. polystyrene). In the former case the risk of sinking of the structure is not negligible. The width and depth (draft) are usually limited to a few meters.

Fig. 2. Box breakwaters[2].

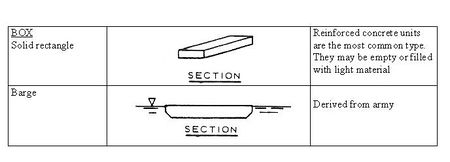
Pontoon breakwaters

Pontoon type breakwaters (figure 3) are effective since the overall width can be of the order of half the wavelength. In this case the expected attenuation of the wave height is significant.

Fig. 3. Different types of pontoon breakwaters[2][6]

Mat breakwaters

Within the mat category, the most used are made with tires. They have a low cost, they can be removed more easily, they can be constructed with unskilled labour and minimal equipment, they are subjected to lower anchor loads, they reflect less and they dissipate relatively more wave energy. However, they are less robust and suitable only in mild wave climates (significant wave height less than 0.5 m).

Fig. 4. Mat breakwaters[2]

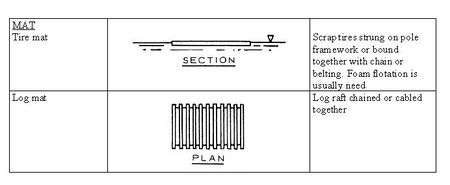
Other types of mat breakwaters are made of horizontal flexible porous membranes. The porosity of membranes contributes to viscous wave energy dissipation. Wave attenuation is increased by adding more mat layers[7]. A wave transmission coefficient (ratio of transmitted to incident wave height) below 0.8 can be achieved only if the membrane width is greater than a half wavelength.

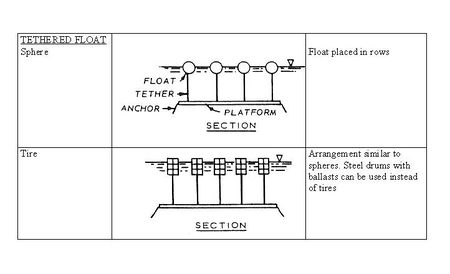
Tethered float breakwaters

Tethered float types are not much used. Two schemes are shown in figure 5.

Fig. 5. Tethered float breakwaters[2]


Mooring, connection forces and failure modes

Floating-breakwater failures are often caused by structural, connection or mooring problems rather than by insufficient hydraulic attenuation alone. Important design and maintenance issues include:

  • mooring-line tension, fatigue and abrasion;
  • anchor capacity and seabed geotechnical conditions;
  • loads and deformation limits of piles or dolphins in shallow-water mooring systems;
  • fatigue and overload of connections between modules;
  • resonance and high instantaneous loads during energetic wave conditions;
  • inspection and maintenance after storms;
  • progressive failure after the loss of one or more mooring lines or connections.

These aspects should be considered together with wave transmission, because a design with good attenuation performance may still be unsuitable if the associated mooring or connection loads are excessive.


Wave transmission

Fig. 6. Rough relation between the transmission coefficient [math]H_t / H_i[/math] and the ratio [math]L/W[/math] between the wavelength [math]L[/math] and the width of the floating structure [math]W[/math].

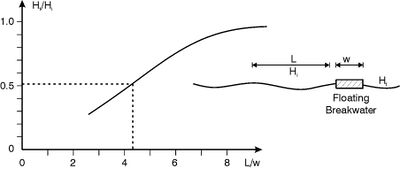
Many laboratory experiments have been performed to establish empirical formulas for the wave transmission of floating breakwaters, especially for the box-type breakwaters[8][9][10][11]. The parameters considered in these experiments are the width [math]W[/math] (along the wave propagation direction), the draft [math]D[/math], the incident wave height [math]H_i[/math] (most experiments considered regular waves), the wavelength [math]L[/math] and the depth [math]h[/math]. The dependence of the wave transmission coefficient [math]C_t=H_t/H_i[/math] (where [math]H_t[/math] is the transmitted wave height) on these various parameters shows a fairly large spread between the different experiments. In general, the wave-height transmission coefficient [math]C_t[/math] decreases when the floating breakwater interacts more strongly with the water column and the incident wave motion. Thus the transmission coefficient tends to decrease for increasing values of [math]D/L[/math], [math]D/h[/math] and [math]H_i/h[/math] and to increase for increasing values of [math]L/W[/math]. The transmission coefficient is most sensitive to the ratio [math]L/W[/math], but also depends (although to a lesser degree) on draft, freeboard, mooring stiffness, module spacing, wave steepness, obliquity, directional spreading and nonlinear effects.

As a rule-of-thumb the transmission varies between [math]H_t / H_i = 0.3[/math] for [math]L/W = 3[/math] and [math]H_t / H_i = 0.9 – 1.0[/math] for [math]L/W = 8[/math], see figure 6.

Consider the example of a pontoon width of [math]W =[/math] 3 m in 2 m deep water, and a requirement of a wave transmission of [math]H_t / H_i \lt 0.5[/math]. In this case the wavelength should be smaller than [math]L \lt 4.3 W \approx 13[/math] m, which corresponds to an approximate wave period of [math]T \approx 3 [/math] s. Floating breakwaters are therefore mainly suitable for waters with limited fetch or otherwise short-period wave climates. They are generally unsuitable as primary structural solutions at moderately exposed and exposed locations.


Designs that enhance wave attenuation

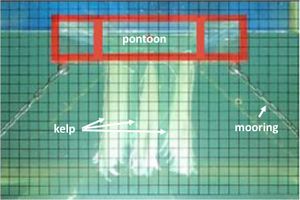
Experiments have been carried out to test various designs that may improve the wave attenuation effectiveness of floating breakwaters. One type of design consists of fixing underneath the breakwater vertical elements that interfere with the wave orbital motion. Tested vertical elements include porous steel plates[12], underhanging flexible curtains[13], curtains consisting of kelp[14] (Fig. 7) and elements made of sponge materials (e.g., polyurethane), that dissipate wave energy[15]. A design with steel wings fixed at selected corners around the breakwater also shows good performance to increase wave reflection and wave dissipation, resulting in a smaller transmission coefficient[16].


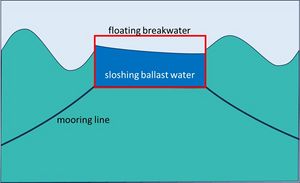
Fig. 7. A curtain of (artificial) kelp absorbs and dissipates wave energy
Fig. 8 Breakwater filled with ballast water that absorbs and dissipates wave energy through sloshing


Another design, shown in Fig. 8, consists of a floating breakwater filled with ballast water. This breakwater utilizes the kinetic and potential energy of the ballast water, which can absorb and dissipate wave energy through the nonlinear sloshing response, thereby achieving effective wave energy attenuation and reducing wave impact. The sloshing ballast water improves the wave dissipation performance of a floating breakwater by up to 20 %. [17][18]

Many of these enhanced designs have shown promising results in laboratory or numerical studies, but their field performance also depends on durability, marine growth, fatigue, maintenance requirements, constructability and mooring loads.


Appendix

Fig. A1. Balance of vertical forces on a buoyant body in a wave field .

This appendix presents a highly simplified model for the interaction between a long rectangular floating breakwater and a perpendicularly incident monochromatic wave field. It illustrates why heave-induced dissipation decreases rapidly for longer waves. It focuses on heave-related viscous dissipation, while much of the attenuation of box and pontoon breakwaters comes from reflection, radiation and induced breaking. For the design of a floating breakwater more advanced models are required that take these effects into account.

The vertical motion [math]\zeta(t)[/math] of the breakwater at [math]x=0[/math] in the wave field [math]\eta(x,t)=a \cos(kx-\omega t)[/math] is described by the heave equation (Archimedes' law, see figure A1):

[math]M \, \Large\frac{\partial^2 \zeta}{\partial t^2}\normalsize = - \rho g \, A \, D + A \, p(z,t) - F_d - F_m \, , \quad z = -D + \zeta(t) . \qquad (A1)[/math]

Meaning of the symbols: [math]F_d=[/math] damping force, [math]F_m[/math] added (entrained) mass force, [math]M=[/math] body mass, [math]A=[/math] horizontal body section area, [math]D=[/math] still water body draft, [math]p=[/math] pressure, [math]h=[/math] water depth, [math]a=[/math] wave amplitude, [math]\omega=[/math] radial wave frequency, [math]k=[/math] wave number, [math]\rho=[/math] seawater density, [math]g=[/math] gravitational acceleration. We assume a long breakwater with uniform conditions along its length. In this case [math]M[/math] is the mass per unit length and [math]A[/math] is the surface per unit length, which is equal to the width [math]W[/math] of the breakwater.

The moving body generates waves and accelerates the surrounding fluid. These effects give rise to added mass and radiation damping. In addition, flow separation, vortex generation and turbulence around the body produce viscous dissipation. In the simplified model used here, these processes are not treated separately. They are represented by an empirical damping force opposing the vertical velocity of the body relative to the surrounding wave motion,

[math]\; F_d = \Large\frac{4}{3 \pi}\normalsize C_d \, \rho \, W \, a \, \omega \, \dfrac{\partial (\zeta - \eta)}{\partial t}\normalsize , [/math]

where [math]C_d[/math] is a dimensionless friction coefficient of order 1[19]. Other body motions (e.g. pitch, roll, sway) are ignored for simplicity.

According to linear wave theory (see Shallow-water wave theory), the pressure is given by

[math]p(-D+\zeta,t) = \rho g \, D - \rho g \, \zeta + \rho g \, K_p(-D+\zeta) \, \eta(t) , \qquad (A2)[/math]

where [math]K_p(-D+\zeta) \approx K=K_p(-D) = \Large\frac{\cosh(k(h-D))}{\cosh(kh)}\normalsize . [/math]

Energy dissipation damps the free oscillations of the buoyant body and causes a phase shift [math]\phi[/math] with respect to the wave motion. Assuming waves of small amplitude, small dissipation and neglecting the influence of inertia of the surrounding fluid, the vertical motion of the body will have the form

[math]\zeta(t) \approx \zeta_0 \, \cos(\omega t - \phi). \qquad (A3)[/math]

Substitution in Eqs. (A1) and (A2) gives

[math]\zeta_0 \approx a \, \sqrt{\Large\frac{K^2+b^2}{(1-m)^2+b^2}\normalsize} , \quad b = \Large\frac{4 a \omega^2}{3 \pi g}\normalsize C_d , \quad m = \Large\frac{M \omega^2}{\rho g W}\normalsize = \Large\frac{D \omega^2}{g}\normalsize , \qquad (A4)[/math]

where we have used Archimedes' law. The draft [math]D[/math] should be chosen such that resonance [math]m=1[/math] under energetic wave conditions is avoided.

The phase shift [math]\phi[/math] is given by

[math]|\zeta_0| \, \cos \phi = a \, \dfrac{K(1-m)+b^2}{(1-m)^2+b^2}. \qquad (A5)[/math]

The energy dissipated by the floating breakwater is given by

[math]dissipation = \dfrac{4 C_d}{3 \pi} \rho W a \omega \Big\langle \Big( \dfrac{\partial (\zeta -\eta)}{\partial t} \Big)^2 \Big\rangle = \dfrac{4 C_d}{3 \pi} \rho W a \omega^3 \Big\langle \Big( |\zeta_0| \cos(\omega t-\phi) – a \cos(\omega t) \Big)^2 \Big\rangle \, , \qquad (A6)[/math]

where [math]\langle … \rangle[/math] denotes the average over the wave period.

Using Eqs. (A4) and (A5), the result is

[math]dissipation = \dfrac{2 C_d}{3 \pi} \rho W a^3 \omega^3 \dfrac{(K+m-1)^2}{(1-m)^2+b^2} \, . \qquad (A7) [/math]

The draft [math]D[/math] is generally much smaller than the still water depth [math]h[/math], implying [math]K \approx 1[/math]. In situations where the wave period is around 5 seconds or more, order of magnitude estimates are [math]m= D \omega^2 / g \lt \lt 1 [/math], and [math]b \lt \lt 1[/math]. As in shallow water [math]\omega[/math] is inversely related to the wavelength [math]L[/math], equation (A7) shows that the dissipation is a rapidly decreasing function of the wavelength. In deeper water the precise dependence differs, but the qualitative conclusion remains the same: long waves are much less effectively attenuated.

Comparison with the wave energy flux entering shallow water ([math] \sim \frac{1}{2} \rho g a^2 \sqrt{gh}[/math]) shows that only a small fraction of the incident wave energy is dissipated by the vertical motion of the floating breakwater for waves with periods of a few seconds or more. For waves with periods not much longer than a few seconds, damping is mainly caused by wave breaking on the breakwater rather than by its motion.


Related articles

Detached breakwaters
Detached shore parallel breakwaters
Port breakwaters and coastal erosion
Applicability of detached breakwaters


References

  1. ↑ 1.0 1.1 Hales, L.Z. 1981. Floating Breakwaters: State-of-the-Art Literature Review. US Army Corps of Engineers Technical Report 81-1
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 McCartney, B. 1985. Floating breakwater design, J. of Waterway, Port, Coastal and Ocean Engineering 111: 304-318
  3. ↑ Van Duy, D., Van Ty, T., Tan Phat, L., Thu Minh, H.V., Giang Nam, N.D., Downes, N.K., Avtar, R. and Tanaka, H. 2025. Simulating the Coastal Protection Performance of Breakwaters in the Mekong Delta: Insights from the Western Coast of Ca Mau Province, Vietnam. J. Mar. Sci. Eng. 13, 1559
  4. ↑ Cebada-Relea, A.J., Lopez, M., Claus, R. and Aenlle, M. 2023. Short-term analysis of extreme wave-induced forces on the connections of a floating breakwater. Ocean Engineering 280, 114579
  5. ↑ Martinelli, L. and Ruol, P. 2006. 2D Model of Floating Breakwater Dynamics under Linear and Nonlinear Waves, 2nd Comsol User Conference, 14 Nov., Milano
  6. ↑ Li, C., Zhang, H., Zhang, H., Sun, B. and Yang, S. 2022. Wave-attenuation and hydrodynamic properties of twin pontoon floating breakwater with kelp. Applied Ocean Research 124 (2022) 103213
  7. ↑ Guo, Y.C., Mohapatra, S.C. and Guedes Soares, C. 2023. Experimental performance of multi-layered membrane breakwaters. Ocean Engineering 281, 114716
  8. ↑ Koutandos, E. and Prinos, P. 2005. Design formulae for wave transmission behind floating breakwaters. XXXI IAHR congress, paper 4081
  9. ↑ Alizadeh, M.J., Kolahdoozan, M., Tahershamsi, A. and Abdolali, A. 2014. Experimental Study of the Performance of Floating Breakwaters with Heave Motion. Civil Engineering Infrastructures Journal 47(1): 59 – 70
  10. ↑ Moghim, N. and Botshekan, M. 2017. Analysis of the performance of pontoon-type floating breakwaters. Hong Kong Institution of Engineers Transactions 24: 9–16
  11. ↑ Elsheikh, A.K., Mostafa, Y.E. and Mohamed, M.M. 2022. A comparative study between some different types of permeable breakwaters according to wave energy dissipation. Ain Shams Engineering Journal 13, 101646
  12. ↑ Cho, I. 2016. Transmission coefficients of a floating rectangular breakwater with porous side plates. Int. J. Nav. Arch. Ocean 8: 53–65
  13. ↑ He, F., Pan, J., Li, J., Zheng, S. and Yuan, Z. 2024. An experimental study of a rectangular floating breakwater with flexible curtains as wave-dissipating components. Appl. Ocean Res. 152, 104185
  14. ↑ Li, C., Zhang, H., Zhang, H., Sun, B. and Yang, S. 2022. Wave-attenuation and hydrodynamic properties of twin pontoon floating breakwater with kelp. Applied Ocean Research 124, 103213
  15. ↑ Zhang, H., Sun, B., Li, Z.W. and Wang, F. 2023. Wave attenuation and motion response of floating breakwater with sponge material. Ocean Eng. 277, 114325
  16. ↑ Liu, Z., Wang, Y., Wang, W. and Hua, X. 2019. Numerical modeling and optimization of a winged box-type floating breakwater by smoothed particle hydrodynamics. Ocean Eng. 188, 106246
  17. ↑ Yang, Z., Xie, M., Gao, Z., Xu, T., Guo, W., Ji, X. and Yuan, C. 2018. Experimental investigation on hydrodynamic effectiveness of a water ballast type floating breakwater. Ocean Eng. 167: 77–94
  18. ↑ Yuan, X., Cao, Z., Xue, M-A., Li, L. and Zheng, J. 2025. Experimental study on effects of floating breakwater filled with ballast water on wave attenuation. Ocean Engineering 341, 122720
  19. ↑ Quartier, N., Ropero-Giralda, P., Domínguez, J.M., Stratigaki, V. and Troch, P. 2021. Influence of the Drag Force on the Average Absorbed Power of Heaving Wave Energy Converters Using Smoothed Particle Hydrodynamics. Water 13, 384


Other sources

  • Allyn N., E. Watchorn, W. Jamieson and Y. Gang, 2001. Port of Brownsville Floating Breakwater, Proc. Ports Conference.
  • Briggs M, Y. Ye, Z. Demirbilek and J. Zhang, Field and numerical comparisons of the RIBS floating breakwater, J. of Hydraulic Research, 40(3), 289-301.
  • Gesrah M.R. 2006. Analysis of 5 shaped floating breakwater in oblique waves: I. Impervious rigid wave boards. Applied Ocean Research, 28(5) 327–338.
  • Isaacson M and O.U. Nwogu, 1987. Wave loads and motions of long structures in directional seas, J Offshore Mech Arct Eng 109, 126–132.
  • Isaacson M. (1993): Wave effects of floating breakwaters, Proc. of the 1993 Canadian Coastal Conference, May 4-7, Vancouver, British Columbia, 53-66.
  • Isaacson M. and S. Sinha, 1986. Directional wave effects on large offshore structures, J. of Waterway, Port, Coastal and Ocean Engineering, 112(4), 482-497.
  • Martinelli L., Zanuttigh B., Ruol P., 2007. Effect of layout on floating breakwater performance: results of wave basin experiments . Proc. Coastal Structures '07, Venice.
  • PIANC. Floating breakwaters - a practical guide for design and construction PTC2 report of WG 13 – 1994
  • Richey E.P. (1982): Floating Breakwater Field experience, West Coast. Report MR 82-5, U.S. Army, Corps of Engineers, Coastal Engineering Research Center; Springfield, Va, 64 pp.
  • Ruol P. and Martinelli L., 2007. Wave flume investigation on different mooring systems for floating breakwaters. Proc. Coastal Structure '07, Venice.
  • Sannasiraj S.A., V. Sundar and R. Sundaravadivelu, 1998. Mooring forces and motion responses of pontoon-type floating breakwaters, Ocean Eng., 25 (1), 27-48.
  • Silander, J. 1999 Floating Breakwater and Environment.
  • Tsinker G., 1994. Marine structure engineering: specialized application, Chapman & Hall, International Thomson Publishing Inc.
  • Van der Meer J.W., R. Briganti, B. Zanuttigh and B. Wang, 2005. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change, Coastal Eng., 52(10-11), 915-929.
  • Yamamoto T., 1981. Moored floating breakwater response to regular and irregular waves. Applied Ocean Research 3, 27–36.


The main authors of this article are Piero Ruol, Job Dronkers and Mangor, Karsten
Please note that others may also have edited the contents of this article.
Citation: Piero Ruol; Job Dronkers; Mangor, Karsten ; (2026): Floating breakwaters. Available from http://www.coastalwiki.org/wiki/Floating_breakwaters [accessed on 17-06-2026]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Floating_breakwaters&oldid=82085"