Wave collision on a vertical wall
When irregular waves hit a sea wall, a shock force can occur that lasts for a fraction of a second. This duration is generally too short to affect the stability of the seawall. Shock forces can roughly be divided into 3 categories:
- Well-ventilated shock with a rapid rise in water, for example, as in a surging breaking wave.
- Compression shock where the wave breaks on the wall so that a pocket (or air pockets) of air is trapped and compressed with great energy, then the air explodes upwards giving a high splash.
- Frontal collision shock, the maximum possible shock pressure from a large vertical wavefront, or from a 'water tongue' hitting a local part of the wall. The pressure is much less than a regular hammer shock, which cannot occur, as has been shown theoretically and experimentally.
Contents
Wave splash
It's a beautiful sunny day on the south coast of France with only small ocean waves and people enjoying the beach life. Then suddenly one of the small incoming waves splashes high into the air when it hits the seawall and exerts a shock force as seen in the picture Fig. 1. The wave has formed a kind of plunging breaker near the vertical wall, enclosing an air pocket with an upper 'wave tongue' that compresses the air with great energy. The next moment the wave tongue explodes in upward direction. There are several possible causes. For example, the low backwash of a wave reflected off the wall that meets a new incoming wave to form the collapsing breaker. Or maybe overriding waves with different frequencies generated offshore by incidental causes. Looking at the small ocean waves in the picture, there seems to be no specific wave that will create a shock force. When such small waves can make such impressive splashes it is understandable that huge storm waves can make very destructive high splashes.
Wave collision shock
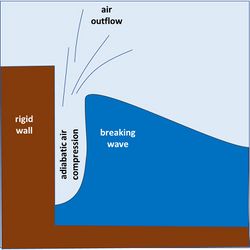
The splashing 'compression shock' force is big, but not as big as the shorter 'frontal collision shock' made by a vertical plane wave front hitting the wall, as shown in Fig. 2. This type of wave shock has been believed to be a water hammer shock. When a metal hammer hits a hard wall an elastic compression wave will travel with the sound velocity from the front to the back of the hammer, so the whole hammer participates in an elastic shock. For the water hammer this gives a pressure
[math]p = \rho \, c \, u \quad[/math], with [math]\quad \rho=[/math] water density, [math]\quad c=[/math] water sound velocity, [math]\quad u=[/math] incoming water velocity.
But the actual pressure is much lower because the water is not trapped like the metal in a hammer, and because of the reaction force of the outflowing air in the narrow air gap. Only the wave front produces a shock force. The water behind will move upwards much like a standing wave. The situation with a large vertical front of the wave hitting the entire wall is extremely rare. In the literature it is suggested that in a compression shock the upper wave tongue will hit the wall with a local direct hammer shock. However, such a large force was not obtained in various experiments in the USA (Kamel, 1968[2]). The 'water hammer' does not hit the wall in vacuum and the water is not solid. The thin air slit between the wave front and the wall (Fig. 2) must be squeezed out, creating a reaction force that slows the water and moves the liquid upwards a fraction of a second before the water hits the wall. Most of the large elastic force is thus avoided. An approximate calculation shows that the shock force can only be about 1/5 of the elastic force (see Jensen, N.M. wave collision shock theory), consistent with the result of the aforementioned American experiments.
Role of the air slit
The air between the wall and the wavefront will either form bubbles in the water, or form small air cushions, that exert a reaction force while being compressed that greatly reduces the speed of the incoming water mass. The air slit almost completely annihilates the elastic hammer compression in the water. Whether it is the whole wave or only a narrow 'tongue' hitting the wall, the escaping air will reduce the shock force. It does not become an elastic water hammer shock because the air between the water and the wall has to escape.
Because the Froude law does not scale aeration effects correctly, physical model test overestimate the maximum forces on the wall, while the durations of the impulses tend to be shorter[3].
Relevance for breakwater design
Harbor structures with a vertical wall facing the incoming ocean waves must be designed to withstand the wave forces. A seawall made of large concrete caissons can locally be subject to high pressures from a shock wave force of very short duration that is relevant for the design of the concrete. Or the entire caisson structure may receive a wave pressure of 2-3 seconds maximum (with a much shorter duration of the impact peak), from large, reflected waves.
[Example: A big wave hits a wall on 10 m water depth with 3 m/sec water velocity. Approximate theory calculates the maximum shock force to 30 m water height pressure (300 kN/m2) (see Jensen, N.M. 1971 frontal collision shock with air slit force). The elastic hammer shock theory gives up to 10 times greater pressure. The vertical breakwater here must therefore be designed to withstand a local pressure of 300 kN/m2, a very local and very short pressure.]
For the stability and foundation of the breakwater, this very short local force may not be relevant, compared to the force on the whole breakwater of much longer duration from a more regular wave, such as a standing wave force (see the formula on the Discussion Page Shallow-water wave theory and Shallow-water wave theory#Vertical Walls).
For further details, see:
An overview of empirical formulas of shock wave impact is given in Cuomo et al. 2010([4].
Related articles
- Shallow-water wave theory
- Waves
- Stability of rubble mound breakwaters and shore revetments
- Seawall
- Extreme storms
References
- ↑ Wiegel R.L. 1964. Oceanographical Engineering. Englewood Cliffs, New Jersey: Prentice Hall
- ↑ Kamel, A.M. 1968. Shock pressure caused by waves breaking against coastal structures. US Army Engineer Waterways Experiment Station, Res. Rep. H- 68- 2
- ↑ Bullock, G.N. and Bredmose, H. 2024. Violent breaking-wave impacts. Part 4: A detailed analysis and comparison of field and 1:4 scale measurements on sloping and vertical walls including the influence of air and scale effects. Coastal Engineering 191, 104520
- ↑ Cuomo, G., Allsop, W., Bruce, T. and Pearson, J. 2010. Breaking wave loads at vertical seawalls and breakwaters. Coastal Engineering 57: 424-439
Please note that others may also have edited the contents of this article.
|
