Wave transmission by low-crested breakwaters

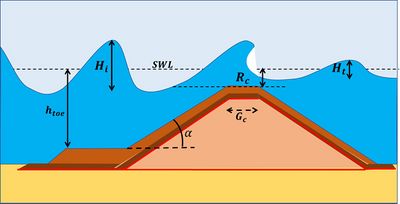
Definition of Low-crested breakwaters: Low-crested breakwaters are manmade wave damping structures in nearshore waters with crest level just above or just below the still water level (SWL). The latter category, also known as submerged breakwater, has a negative freeboard [math]R_c[/math]. This is the common definition for Low-crested breakwaters, other definitions can be discussed in the article

Definition of Transmitted wave: The transmitted wave is the onshore propagating wave after being damped by an artificial or natural obstacle. The wave transmission coefficient [math]K_t[/math] is the ratio of the wave heights of the transmitted and incoming waves. This is the common definition for Transmitted wave, other definitions can be discussed in the article

Fig. 1. Wave transmission over a submerged breakwater at Mandara beach, Alexandria (Egypt). The yellow arrows indicate the location of rip currents.

Notes

Submerged and low-crested breakwaters are specifically designed to mitigate the attack of incoming waves and thereby protect beaches against erosion. While these structures only partially reduce incoming waves, they offer several advantages over high-crested breakwaters. They do not obstruct the view of the sea and allow water circulation and flushing between the structure and the beach. These types of breakwaters are commonly utilized to protect tourist beaches (see Fig. 1). One drawback is the presence of rip currents along the extremities of the breakwater. These rip currents are driven by wave-induced water level set-up at the onshore side of the breakwater.

Fig. 2. Wave transmission over a low-crested breakwater and mathematical symbols. The freeboard [math]R_c[/math] is negative when the breakwater crest is below the still water level [math]SWL[/math].

The wave transmission performance of a low-crested breakwater is expressed by means of the wave transmission coefficient [math]K_t = H_t / H_i[/math]. The transmission coefficient depends primarily on (see Fig. 2):

• the freeboard [math]R_c[/math], the distance between the breakwater crest level and the still water level (negative for a submerged breakwater)
• the width [math]G_c[/math] of the breakwater crest
• the spectral wave height [math]H_i[/math] of the incoming wave at the toe of the structure (approximately equal to the significant wave height, see Statistical description of wave parameters)
• The wave conditions, represented by the surf similarity parameter [math]\xi = \Large\frac{\tan \alpha}{\sqrt{H_i / L}}[/math].

Meaning of the symbols:

• [math]H_t[/math] the spectral height of the transmitted wave
• [math]L = g T_p^2 / (2 \pi)[/math] the wavelength of the incident wave
• [math]T_p[/math] the peak spectral wave period
• [math]\tan\alpha[/math] the slope of the structure
• [math]g[/math] the gravitational acceleration

Several empirical expressions for the wave transmission coefficient have been derived from laboratory experiments and tested in field situations. A frequently used formula, was established by D’Angremond et al. (1997) for unbroken waves and for the range [math]0.075 \lt K_t \lt 0.8[/math],

[math]K_t \equiv \Large\frac{H_t}{H_i}\normalsize = c_1 \Large\frac{R_c}{H_i}\normalsize + c_2 \Big( \Large\frac{G_c}{H_i} \Big)^{c_3} \normalsize [1 - \exp(c_4 \xi)] , \qquad (1) [/math]

where [math]c_1=-0.4, \; c_2=0.8, \; c_3=-0.31, \; c_4=-0.5[/math]. For permeable breakwaters (e.g. rubble-mound breakwaters with porosity of about 0.5) the coefficient [math]c_2=0.8[/math] should be replaced by [math]c_2=0.64[/math].

Application of this formula to over 4000 available laboratory and field data showed that 62% of data falls within a confidence level of 20% and 87% of data falls within a confidence level of 50%.

Since it was observed that this formula overestimates the wave transmission of wide-crested breakwaters ([math]G_c / H_i \gt 10[/math]), an adjusted set of parameters for this case was proposed by Briganti et al. (2004) with coefficients [math]c_1=-0.35, \; c_2=0.51, \; c_3=-0.65, \; c_4=-0.41[/math].

Wave attenuation can also be obtained with biogenic reefs instead of rubble-mound or other artificial submerged structures. Wave attenuation by oyster reefs is dealt with in the article Oyster reef shore protection.

Fig. 3. Graphical estimate of the wave transmission coefficient as a function of the relative freeboard, based on laboratory data. The red glow of the curve indicates the level of accuracy.

Noticing the weak dependence of the transmission coefficient on the wave steepness and the slope of the structure, Van Gent et al. (2023) derived from a series of flume experiments the alternative formula,

[math]K_t = c_5 + c_1 \tanh \Bigg(c_4 - \Large\frac{R_c}{H_i}\normalsize - c_2 \bigg( \Large\frac{G_c}{L} \bigg)^{c_3} \normalsize \Bigg) , \qquad (2)[/math]

where [math]c_1=0.47, \; c_2=3.1, \; c_3=0.75, \; c_4=0, \; c_5=0.5 [/math] for impermeable smooth structures. For permeable structures (e.g. rubble-mound, with porosity of about 0.5) the values of the coefficients [math]c_1, c_4[/math] should be replaced by [math]c_1=0.43, \; c_4=0.25[/math]. The formula (2) was established for a series of experiments with [math]\; -2.5\lt R_c/H_i \lt 2.5, \; 0.017 \lt G_c / L \lt 0.27, \; 0.015 \lt H_i / L \lt 0.033[/math] and trapezoidal structures with slope 1:2.

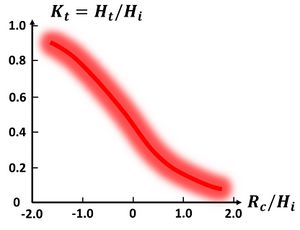
Fig. 3 gives a rough graphical estimate of the transmission coefficient from laboratory data as a function of the relative freeboard.

Huang et al. (2024) conducted flume experiments of wave transmission over artificial reefs with a substantially higher porosity [math]n = 0.68[/math]. From these experiments it appeared that the structure of the porosity plays a role in the wave dissipation, which hampers direct comparison of their results with the experiments of Van Gent. Wave dissipation and transmission depended for high porosity primarily on the extended water depth [math]h_{ce} = - R_c + n h_r, \;\; h_r = h_{toe}+R_c[/math], which takes into account the height [math]n h_r[/math] of pore water in the reef. The crest width was larger than in the experiments of Van Gent. Only a small dependence of the relative crest width [math]G_c/L[/math] on the wave transmission was found. The following formula was proposed for wave transmission over the highly porous reef (for [math]K_t \lt 1[/math]):

[math]K_t \approx 0.13+ 0.4 \Big( (K_{tu} - 0.13) \Large\frac{h_{ce}}{H_i}\normalsize + 0.13 \Big), \;\; H_i \lt 0.4 h_r \, ; \quad K_t \approx K_{tu} \equiv - 0.5 \Large\frac{R_c}{h_r}\normalsize +0.4 , \;\; H_i \gt 0.4 h_r . \qquad (3)[/math]

Related articles

Detached breakwaters

Wave overtopping

Stability of rubble mound breakwaters and shore revetments

Modelling coastal hydrodynamics

References

The main author of this article is Job Dronkers Please note that others may also have edited the contents of this article. Citation: Job Dronkers (2024): Wave transmission by low-crested breakwaters. Available from http://www.coastalwiki.org/wiki/Wave_transmission_by_low-crested_breakwaters [accessed on 24-12-2024] For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Dronkers J