Wavelet analysis of coastal processes
Contents
Introduction
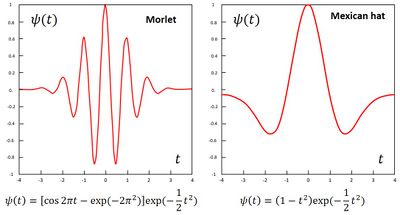
The wavelet technique is similar to a Fourier analysis approach, where the signal is approximated by some basis functions, which in wavelet analysis are simply wavelet functions. The drawback of Fourier analysis or the more general harmonic analysis, in which data are represented by a superposition of sinusoidal terms, is the assumption of cyclicity beyond the spatial or temporal range of the dataset. This assumption may be justified if dominant processes have a linear or weakly non-linear character (see, for example, the article Stability processes), but in practice many morphological features and processes are influenced by highly nonlinear perturbations both in space (e.g., presence of geological sedimentary structures) and in time (e.g., occurrence of extreme storms). In this case no good representation of the dataset can be obtained with a limited number of sinusoidal functions. Wavelets, on the contrary, can represent highly nonlinear behavior and do not assume any cyclicity, as they are localized in space and in time (Burrus et al., 1998[1]). Time resolution is achieved with wavelets by using a scalable modulated window that is shifted along the signal. Hence, generally a small number of wavelets is needed to reconstruct a function with sufficient accuracy. An important property of wavelets is that their mean is zero and their average squared norm is unity. Well-known examples of wavelets are the Mexican hat and the Morlet wavelet, see Fig. A1 of the appendix. These are examples of mother wavelets, which may be dilated and transformed to form the wavelet basis. The first wavelet function was developed by Haar (1910[2]). Wavelets have traditionally been used in data analysis to increase the signal-to-noise ratio, and also to compress the data to only a few wavelet functions.
Application in coastal bathymetry studies
Wavelets were first used in coastal morphodynamics by Sarah Little et al. (1993) [3] to analyze large scale (of the order of 100 to 1000 kms) bathymetric evolution offshore the Hawaian islands; the wavelets the authors adopted for this analysis were Daubechies wavelets (see Appendix), a family of discrete orthogonal wavelets introduced by Ingrid Daubechies (1988)[4]. Based on scale analysis by applying a wavelet transform, the authors were able to discover a small, low-frequency topographic feature of around 200 kms in length, whose details suggest it is a slow-spreading rift. After this pioneering work, other topography identification investigations followed (eg. Little et al., 1996[5]).
In a later investigation, Li et al. (2005)[3] analyzed nearshore beach profile variability at the Duck study site, North Carolina (USA). The space scales in this case were, instead, of the order of 0.1 kms. The objective of the study was to analyze both time and space variability of the bathymetry. The authors also chose Daubechies’ wavelets as a base and an adapted maximum overlap discrete wavelet transform (AMODWT), as both are very suitable for decomposition of signals with strong space and time variations. Data of the bathymetry profile were available from thorough surveys since 1981. Li et al. identified the variance across the profile as nonstationary, with largest variations in the sandbank region; this region occurs between 100 and 400-500 m offshore. Within this region, the 128-256 m spatial scale contained most of the information, and did make the largest contribution to the variance for all the months surveyed. It is worth noting that the largest variations at the 128 m scale occurred in the sandbar region, indicating this is the region where the morphology evolves the most, which is to be expected. Contrary to the spatial scales, the temporal wavelets contributed differently to the total variance depending on the month considered and the position along the profile. The two temporal wavelets that span from 32-64 and 64-128 months, respectively, contained most of the variance. Contributions of lower order appeared as large peaks in the profiles, indicating they are mostly event-related, rather than part of the average trend. This is highlighted by the authors with several examples. This work also proved wavelets are a useful technique in signal decomposition with great potential in coastal research.
Application in storm wave studies
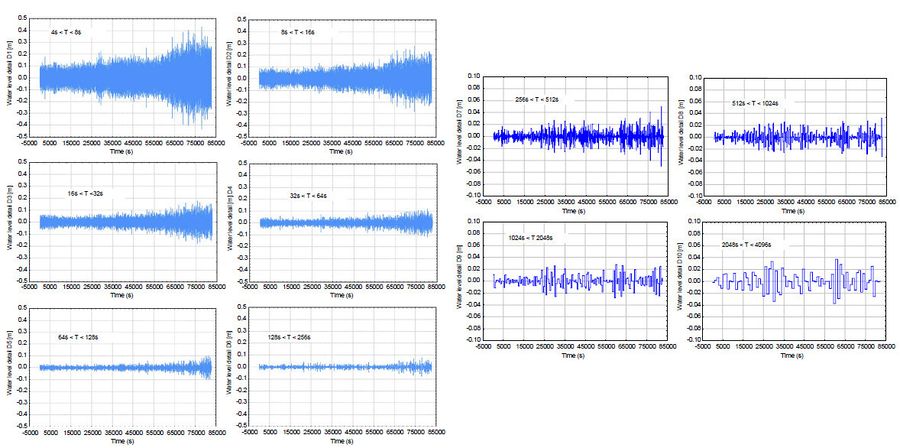
An example how a signal can be decomposed into different spectral bands using orthogonal wavelets was given by Różyński and Reeve (2005) [6]. Fig. 1, left panel, shows the time series of water level at a Baltic Sea coastal segment in Poland featuring a stormy event on 27th Oct. 2002, sampled at the rate of 0.5 Hz. Next, Fig. 1, right panel, presents the results of wavelet decomposition with the orthogonal Haar wavelet (see Appendix) for frequency bands covering wind waves (4 – 8 s), swell (8-16 s) and infragravity waves (16-256 s). The growth of wave height of all those components during the storm buildup can clearly be seen.
Consequently, Fig. 1, right panel, demonstrates residual spectral bands, which are roughly the same throughout the storm. The patterns belonging to each spectral band are called ‘details’ in wavelet terminology, whereas the pattern in Fig. 2 contains elements with periods above 4096 s i.e. the ultra-slow varying trend, featuring the storm surge. This pattern is called ‘smooth representation’ in wavelet terminology. We can see that the storm was decomposed into spectrally disjoint, orthogonal patterns, allowing for their detailed, individual examination; in wavelet terminology the smooth representation and details together are all parts of multi-resolution analysis of a time series. Jagged trajectories of the smooth representation and details describing low-period variability originate from the use of Haar wavelet. More advanced nearly asymmetric dbN (Daubechies[4]) or nearly symmetric coifN wavelets (also constructed by I. Daubechies) do not produce such artefacts.
Appendix A: Introduction to wavelet theory
Continuous Wavelet Transforms (CWT)
Continuous wavelets make it possible to analyze characteristic patterns of signals [math]y(t)[/math] in both the time (or space) domain and the frequency domain. The word 'signal' denotes the outcome of a process; we consider signals of limited length and assume that they are sampled at intervals much smaller than the signal length. The samples form a data record of [math]N[/math] numbers that can be analyzed by numerical methods. In the following, the words signal and data record are sometimes used indiscriminately.
Wavelet analysis is often used in cases where the frequency spectrum of a signal changes with time (or space); examples are data records representing bathymetry, wave registrations and many other common phenomena such as audio recordings. Fourier analysis of a signal [math]y(t) \rightarrow \hat{y}(f) = \int_{-\infty}^{\infty} \, y(t) \, e^{-2 i \pi f t} dt[/math] provides information only on the overall frequency content of the signal. When the frequency spectrum changes significantly along the signal, Fourier analysis requires dividing the signal into separate time (or space) slices. However, since the number of data points in each slice is similar, information about low frequencies is lost, while information about high frequencies may be redundant. Unlike Fourier transforms, wavelets have a time (or space) window that is moved along the signal and has a length that is adapted to each frequency domain studied. They are suitable not only for signal characterization, but also for signal compression.
Different types of wavelet functions [math]\psi(t)[/math] can be used; a few examples are shown in Fig. A1. The functions [math]\psi(t)[/math] in these examples are so-called 'mother wavelets' which probe a frequency domain around 1 Hz and a time window around [math]t=0[/math]. They are generalized by adapting the frequency domain and the time origin,
[math]\psi(t) \longrightarrow \psi_{f_0,t_0}(t) \equiv \psi\big(f_0(t-t_0)\big) , \qquad (A1)[/math]
The continuous wavelet transform [math]T(f_0,t_0)[/math] is the projection of the signal [math]y(t)[/math] on the wavelet component [math]\psi_{f_0,t_0}[/math] for different frequencies [math]f_0[/math] and time origins [math]t_0[/math], the wavelet function thus acting as a filter on the signal:
[math]T(f_0,t_0)=\sqrt{f_0} \, \int_{-\infty}^{\infty} \, dt \, y(t) \, \psi^*\big(f_0(t-t_0)\big) . \qquad (A2)[/math]
The integration extends over the whole signal length; the integration limits can be set to [math]\pm \infty[/math] because the wavelet function is practically zero for large [math]|t|[/math]. The symbol [math]\psi^*[/math] stands for the complex conjugate of [math]\psi[/math] when the wavelet is represented by a complex function (e.g. the Morlet wavelet); the real value should be considered for physical interpretation. Large values of [math]T(f_0,t_0)[/math] are indicative of time windows around [math]t_0[/math] where the dominant frequencies in the time series are close to [math]f_0[/math].
Although the wavelet family [math]\psi_{f_0,t_0}(t)[/math] does not constitute an orthogonal basis, it is nevertheless possible to reconstruct the original time series from the transforms [math]T(f_0,t_0)[/math]. By using Fourier transforms it can be shown that
[math]y(t)=\Large\frac{1}{C}\normalsize \, \int_{-\infty}^{\infty} \, dt_0 \, \int_{0}^{\infty} \, df_0 \, \psi\big(f_0(t-t_0)\big) \, T(f_0,t_0), \quad C = \int_0^{\infty} \, \Large\frac{df}{f}\normalsize \, |\hat{\psi}(f)|^2 , \quad \hat{\psi}(f) = \int_{-\infty}^{\infty} \, \psi(t) e^{-2 i \pi f t} dt , \qquad (A3)[/math]
where it is assumed that [math]\hat{\psi}(0)=0[/math].
Wavelet analysis of datasets is often carried out with the Morlet wavelet function (Fig. A1)
[math]\psi_{f_0}(t) = \large \big(e^{2 i \pi f_0 t} – e^{-½ (2 \pi f_0)^2 } \big) e^{ -½ t^2} \normalsize . \qquad (A4)[/math]
The Fourier transform of this complex wavelet function is focused around [math]f=f_0[/math] and has only positive frequencies,
[math]\hat{\psi_{f_0}}(f) = \sqrt{2 \pi} \Big[ \large e^{- 2 \pi^2 ( f - f_0)^2} – e^{- 2 \pi^2 (f^2 + f_0^2)}\normalsize \Big]. \qquad (A5)[/math]
The review by Addison (2018[7] gives more detailed information on continuous wavelet transforms.
Discrete Wavelet Transforms (DWT)
The continuous wavelet transform still contains considerable redundant information on the analyzed dataset and takes much computation time. Discrete wavelet transforms do not have these disadvantages and are often used for reduction of datasets that otherwise require large storage space. It is often used for image processing or for the compression of audio records.
The Haar wavelets
An example of a discrete wavelet is the Haar wavelet:
[math]H(t) = 1 , \; 0 \le t \le ½ ; \;\; H(t) = -1 , \; ½ \le t \le 1 ; \; \; H(t) = 0 , \; t \lt 0, \; t \gt 1 \qquad (A6) [/math]
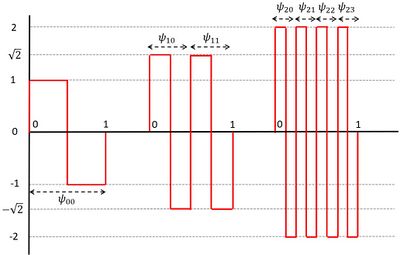
We consider here a signal [math]y(t)[/math] covering the interval [math]0 \le t \le 1[/math], sampled at [math]N=2^{n+1}[/math] equidistant times [math]t_i[/math]. From the Haar wavelet (the 'mother' wavelet) we construct the wavelet family (see Fig. A2)
[math]\psi_{jk}(t) = 2^{j/2} \, H(2^j \, t - k) , \; \; j=0, 1, .., n ; \; k = 0 , .., 2^j – 1 . \qquad (A7)[/math]
These wavelets form a complete orthonormal basis on the interval [math]0\lt t\lt 1[/math],
[math] \lt \psi_{jk}(t)\, \psi_{lm}(t)\gt = \int_0^1 \psi_{jk}(t) \, \psi_{lm}(t) \, dt = \delta_{jl} \, \delta_{km} , \qquad (A8)[/math]
where [math]\delta_{jj}=1, \; \delta_{jl}=0, \; j \ne l[/math].
It can be shown that every continuous function [math]y(t)[/math] in the interval [math]0 \le t \le 1[/math] can be decomposed in a series of Haar wavelets with components [math]y_{jk}=\lt y(t)\, \psi_{jk}(t)\gt [/math],
[math]y(t) \rightarrow \lt y(t)\gt + \sum_{j=0}^n \, \sum_{k=0}^{2^j-1} \, y_{jk} \, \psi_{jk}(t) , \; n \rightarrow \infty . \qquad (A9)[/math]
The Haar wavelets can be thought of as filters that extract information from the signal [math]y(t)[/math] at successive levels of detail. The lowest level of detail is obtained by taking the average; this corresponds to projecting the signal [math]y(t)[/math] on the scale wavelet (also called 'father wavelet') [math]\phi(t) = 1, \; 0 \le t \le 1; \; \phi(t)=0[/math] elsewhere. The next level of detail is obtained by applying the filters [math]\psi_{10}, \, \psi_{11}[/math]. The filters [math]\psi_{n0}, \, \psi_{n1}, ……, \psi_{n2^{n-1}}[/math] give the highest level of detail. Applying all filters to the signal yields more numbers (signal components) than the data record. However, many signal components make very small contributions; in practice this is especially true for wavelet projections with the highest levels of detail (large [math]j[/math]). Removing these small components generally greatly reduces the amount of information (number of components) required for an accurate representation of the signal.
The step functions make the Haar wavelets computationally fast and easy to implement, but limit the ability of Haar wavelets to represent smooth functions. For that reason, other discrete wavelets have been developed.
The Daubechies wavelets
The most popular alternative to the Haar wavelets are the Daubechies wavelets, which can be considered a generalization of the Haar wavelets. The Daubechies wavelet family, named after the Belgian mathematician Ingrid Daubechies, is smooth and forms an orthonormal basis. There is no explicit expression for the Daubechies wavelets; they are constructed iteratively by a recursive method. The mother wavelet [math]\psi(t)[/math] is constructed as a sum of the scaling functions [math]\phi(t)[/math], which satisfy
[math]\phi(t)= \sum_{k=0}^{N_D -1} a_k \, \phi(2t-k), \quad \lt \phi(t)\gt \equiv \int_{-\infty}^{\infty} \phi(t) \, dt = 1 \; \longrightarrow \; \sum_{k=0}^{N_D -1} a_k = 2 , \qquad (A10)[/math]
and orthonormality conditions
[math]\lt \phi(t)\, \phi(t+m)\gt \equiv \int_{-\infty}^{\infty} \phi(t) \, \phi(t+m) \, dt = \delta_{0m} \; \longrightarrow \; \sum_{k=0}^{N_D -1} a_k \, a_{k+2m} = 2 \delta_{0m} , \qquad (A11)[/math]
where the even number [math]N_D[/math] is the order to which the system is determined. The Daubechies mother wavelet is defined by
[math]\psi(t) = \sum_{k=0}^{N_D-1} (-1)^k a_{N_D-1-k} \, \phi(2t-k) . \qquad (A12)[/math]
It is orthogonal to the scaling function [math]\phi(t)[/math] because [math]\sum_{k=0}^{N_D -1} (-1)^k a_{N_D -1-k} a_k = 0[/math].
The distinctive feature of Daubechies wavelets is the property that they can represent exactly any polynomial expression to order [math]N_D/2-1[/math]. This yields the condition
[math]\sum_{k=0}^{N_D-1} a_k k^m = 0, \; \; m=0, .., N_D/2-1 , \qquad (A13)[/math]
which can be derived by expanding [math]t^m[/math] as [math]t^m = \sum_{k=0}^{N_D/2-1} c_k \, \phi(t-k)[/math] and noting that [math]\lt \phi(t-k) \, \psi(t)\gt = 0[/math]. The coefficients [math]a_k[/math] can be uniquely determined from the conditions (A10), (A11) and (A13).
The functions [math]\phi(t)[/math] can be constructed by sampling at integer values [math]t=1, t=2[/math], etc. and noting that [math]\phi(t)=0, \; t \lt 0; \; t \gt N_D-1[/math]. This yields a set of [math]N_D[/math] equations
[math]\phi(0)=a_0 \phi(0), \; \phi(1)=a_0 \phi(2)+a_1 \phi(1)+a_2 \phi(0), \;…. \; , \phi(N_D -2)=a_{N_D -3} \phi(N_D -1)+a_{N_D -2} \phi(N_D -2)+a_{N_D -1} \phi(N_D -3), \; \phi(N_D -1)=a_{N_D -1} \phi(N_D -1)[/math]
from which the values [math]\phi(0), \phi(1), \phi(2)[/math], etc. can be determined up to a multiplicative factor. This factor is determined by the condition (A10) that yields [math]\sum_{k=0}^{N_D-1} \phi(k)=1[/math]. The values at half integers can also be determined by using the equality (A10):
[math]\psi(t/2) = \sum_{k=0}^{N_D -1} a_k \, \phi(t-k) . \qquad (A14)[/math]
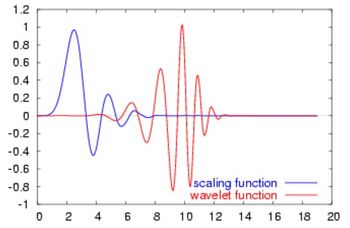
and further fractions [math]t/4, \, t/8[/math], etc. similarly in next iteration steps. After a number of iterations, the Daubechies scaling function [math]\phi(t)[/math] and mother wavelet [math]\psi[/math] can be determined to the desired accuracy. The scaling function and mother wavelet function of order [math]N_D=20[/math] are shown in Fig. B2. The wavelet family is derived from the mother wavelet in the same way as for the Haar wavelet and forms an orthonormal basis:
[math]\psi_{jk} (t) = 2^{j/2} \, \psi^w (2^j t -k) , \quad \lt \psi_{jk} (t) \, \psi_{lm} (t) \gt = \delta_{jl} \, \delta_{km} , \qquad (A15)[/math]
where [math]\psi^w (2^j t -k)[/math] is the rescaled wavelet function, wrapped to the unit interval [math][0,1][/math] and [math] \lt ..\gt [/math] stands for integration over this unit interval. When the signal [math]y(t)[/math] is also scaled to the interval [math][0,1][/math], then it can be written, for large [math]N_D[/math], as a superposition of Daubechies wavelets,
[math]y(t) = \lt y(t)\gt + \sum_{j=0}^{N_D} \sum_{k=0}^{2^j -1} c_{jk} \, \psi_{jk}(t) , \quad c_{jk} = \lt y(t) \, \psi_{jk}(t) \gt . \qquad (A16)[/math]
In practice, it can be necessary for large data records to use Daubechies wavelets of high order ([math]N_D[/math] of about hundred). The construction of such high order Daubechies wavelets is laborious, but they are available in many software packages developed for data processing.
The reviews by Williams and Amaratunga (1994[8]) and Rowe and Abbot (1995[9]) give more detailed information on discrete wavelet transforms.
Related articles
References
- ↑ Burrus, C. S., R. A. Gopinath and Guo, H. 1998. Introduction To Wavelets And Wavelet Transforms, A Primer. Prentice Hall, USA.
- ↑ Haar A. 1910. Zur Theorie der orthogonalen Funktionensysteme, Mathematische Annalen 69: 331-371
- ↑ 3.0 3.1 Little, S.A., Carter, P. and Smith, D. 1993. Wavelet analysis of a bathymetric profile reveals anomalous crust. Geophysical Research Letters 20: 1915-1918
- ↑ 4.0 4.1 Daubechies I. 1988. Orthonormal Bases Of Compactly Supported Wavelets. Communications on Pure and Applied Mathematics 41: 909-996
- ↑ Little, S. A. and Smith, D.K. 1996. Fault scarp identification in side-scan sonar and bathymetry images from the mid-atlantic ridge using wavelet-based digital filters. Marine Geophysical Researches 18: 741-755
- ↑ Różyński, G., Reeve, D. 2005. Multi-resolution analysis of nearshore hydrodynamics using discrete wavelet transforms. Coastal Engineering 52: 771-792
- ↑ Addison PS. 2018 Introduction to redundancy rules: the continuous wavelet transform comes of age. Phil. Trans. R. Soc. A 376: 20170258.
- ↑ Williams, J. and Amaratunga, K. 1994. Introduction to wavelets in engineering. International Journal for Numerical Methods in Engineering, Wiley 37: 2365-2388 https://hal.archives-ouvertes.fr/hal-01311772
- ↑ Rowe A.C.H. and Abbott, P.C. 1995. Daubechies wavelets and Mathematica. Computers in Physics 9, 635; doi: 10.1063/1.168556 https://doi.org/10.1063/1.168556
Please note that others may also have edited the contents of this article.
|