Currents and turbulence by acoustic methods

From Coastal Wiki
Jump to: navigation, search



This article shows that acoustic instrumentation is suitable to measure currents and turbulence in the ocean. First, the article introduces how to estimate velocity. Subsequently, the article describes two ways to estimate turbulence. One method is to estimate turbulence by a single instrument, an Acoustic Doppler Current Profilers (ADCP), combining the variance method and the structure function method. The other is a more direct method to estimate turbulence using an Acoustic Doppler Velocitymeter (ADV). Nowadays, the measurement of turbulence with ADVs has become a standard way to estimate turbulence. The inertial dissipation method can be used to calculate relevant turbulence parameters when ADVs are used for measurements.

Acoustic methods for estimating of velocity

Principles of velocity calculation by Doppler shift

To measure currents in the ocean, Acoustic Doppler Current Meters - Velocimeters (ADVs) and Profilers(ADCPs)- are used. The original idea is to use the "Doppler shift" to calculate velocity. The Doppler shift is the observed change of sound pitch as result from relative motion. An example of Doppler effect is the sound made by a vehicle approaches, i.e. a car has a higher pitch as it approaches and lower as it goes away. This change in pitch is proportional to how fast the vehicle is moving (this the same technique used by speed cameras and speed guns used by police). So if we can measure how much the pitch changes we can measure how fast the vehicle goes.

The acoustic method for measuring velocity is based on the principle of the Doppler shift, involving the speed of sound. The speed of sound is:

[math]C=F\times\lambda[/math],

where [math]F[/math] is the sound frequency, [math]\lambda[/math] is the sound wave length .

The Doppler shift is the difference between the frequency when there is no movement and the difference when either the target or the source or both are moving and is:

[math]F_D = F \, {C \over V}[/math],

where [math]F_D[/math] is the Doppler Shift, [math]V[/math] is the is the relative velocity between source and receiver and [math]C[/math] the speed of sound.

In the case of all the acoustic Doppler profilers and current meters (but not velocimeters) the transducer works as both a transmitter and a receiver, so that the equation changes to:

[math]F_D = 2F \,{C \over V}[/math]

So if we know the original frequency and velocity of sound we can measure the frequency change and infer the along sound (beam) velocity. Because it is only possible to measure the along beam velocity, instruments have 3 or 4 transducers, so that the 3 velocity components can be measured. The problem of this technique, as used in the profilers, is that each along beam velocity is measuring a different part of the water, so we have to assume that the velocity movement is the same within that area.

All commercial Doppler profilers and current meters (not the velocimeters) are capable to use this technique (Narrow Band). The most popular instruments available are instruments from Teledyne RD Instruments, SonTekNortek and Aanderaa

Principles of velocity calculation by broadband and coherent techniques

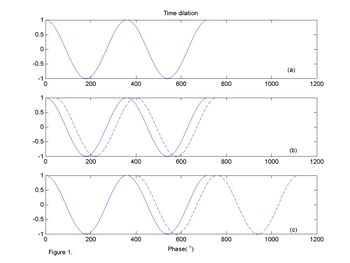
Until now we have considered the Doppler effect in terms of frequency, but to understand how Broadband (patented by RDI) and the phase coherent techniques we have to discuss the signal changes in the time domain, this is termed time dilation.

When sending a pulse of sound to a stationary particle, the echo from this pulse of sound will remain the same (Figure 1a). If the particle moves away from the transmitter it will take longer to the sound to go back and forth (Figure 1b). This change in travel time caused by the distance travelled is called propagation delay.

Echoes from a particle always look the same when the particle does not move, i.e. there is no propagation delay. Echoes have the same relative phase which means zero phase change. In the case of superimposing a second echo on a particle moving away from the transducer, the second echo would be delayed with respect of the first one. In the case of the example shown in figure 1a, the delayed echo shown as a dashed line, has a phase delay of 40o. A propagation delay corresponds to a change in distance, so if we measure the delay and we know the speed of sound we can estimate how far the particle has moved and because we know the time lag between pulses we can calculate the particle velocities.

Figure 1: Time dilation

The main problem of measuring the phase is that phase can only be measured between 0 and 360o; once it reaches 360o it starts again at 0o. So in the case of the example in figure 1, a change of 40o or a change of 400o would be the same; this is called phase ambiguity. To solve this problem we need to figure out how many times the phase has passed through 360o; this is called ambiguity resolution.

Broadband and pulse coherent techniques use the autocorrelation method to process complicated real-world echoes to obtain velocity. In pulse coherent processing, two pulses are emitted into the water. As explained before, the change in phase between the pulse pair is measured so that each pulse pair produces a single velocity estimate and thus the pair is defined as a ping. The time between the two pulses determines the maximum velocity detectable and also determines the maximum range of the system. There is no other acoustic method that can produce such high precision velocity data with such small cells and rapid sampling (Sontek, 2004[1]). This technique is used by ADV (R) (see also Acoustic point sensors (ASTM, UHCM, ADV) and is available in certain Doppler Profilers from RDI and Sontek. Broadband works by transmitting a series of coded pulses, all in sequence inside a single long pulse, producing many echoes from many scatterers, all combined into a single echo. The propagation delay is extracted by computing the autocorrelation at the time lag separating the coded pulses. The success of this computation requires that the different echoes from the coded pulses (all buried inside the same echo) be correlated with one another (RDI 1996[2]). The advantage of broadband and pulse coherent modes is that the precision of the data is improved enormously in comparison with narrowband (Sontek 2004[1]).

Calculation of three-dimensional velocities

As mention above, each transducer can only measure an along-transducer velocity, so to measure the three components of velocity one needs a minimum of 3 beams. Also because the beams are measuring different water columns, it must be assumed that there is horizontal homogeneity, which is sensible most of the times in shelf seas and estuaries. To explain next how to solve the three dimensional velocities in a four beam array, we chose this configuration for simplicity and also because this is the only configuration that can be used to calculate Reynolds stresses by the variance method (Stacey et al., 1999[3], Lu and Lueck, 1999[4]).The method is based on the fact that an ADCP has two pairs of opposing acoustic beams, and that each beam measures a velocity that is actually a weighted sum of the local horizontal and vertical velocities. The velocities determined for each beam are then given by:

[math]u_1=v \, sin\theta+w \, cos\theta; \quad\quad\quad u_2=-v \, sin\theta+w \, cos\theta[/math]

[math]u_3=u \, sin\theta+w \, cos\theta; \quad\quad\quad u_4=-u \, sin\theta+w \, cos\theta[/math]


where [math]\theta[/math] is the angle of the acoustic beam from the vertical (20° in this case) and [math]u[/math], [math]v[/math] and [math]w[/math] are the horizontal and vertical velocity components. So that:

[math]u=\Large\frac{u_3-u_4}{2sin\theta}\normalsize; \quad \quad v=\Large\frac{u_1-u_2}{2sin\theta}\normalsize; \quad\quad w=\Large\frac{u_1+u_2}{2cos\theta}\normalsize=\Large\frac{u_3+u_4}{2cos\theta}\normalsize[/math]

Estimation of turbulence using Acoustic Doppler Current Profilers (ADCPs)

Estimation of relevant parameters

In the quest to measure and calculate turbulence parameters, the use of Acoustic Doppler Current Profilers (ADCPs) has become common practice in recent years (Stacey et al., 1999[3]; Rippeth et al., 2002[5]; Souza et al., 2004[6]). The main turbulence parameters are:

  • Reynolds stresses
  • Turbulent Kinetic Energy TK production ([math]P[/math])
  • Eddy viscosity ([math]N_z[/math])
  • TKE dissipation ([math]\epsilon[/math])

Great effort has been put to determine the theoretical errors of the method using ADCPs (Williams and Simpson, 2004[7]), and to achieve a clear validation by comparing ADCP Reynolds stresses with estimates from other instruments (Howarth and Souza, 2005[8]; Souza and Howarth, 2005[9]). Therefore we can now have some confidence in the TKE production estimates. More recently Wiles et al. (2006[10]) have used the structure function method to estimate the TKE dissipation (ε), producing promising results, although the dissipation values appear to be slightly underestimated.

The advantage of the ADCP is its simplicity and versatility. The instrument is simple to set and use and will allow you to have a full water column estimate of [math]P[/math], [math]\epsilon[/math] and suspended particulate matter (SPM), and if set-up properly it will also let you have a directional wave spectra.

In order to calculate the Reynolds stresses we need to separate the velocities into mean and fluctuating quantities. Taking the difference between the two opposing beams it can be shown by combining the equations and ensemble average them that:

[math]\lt {u\prime w\prime}\gt =\Large\frac{{\lt u\prime_3^2\gt }-{\lt u\prime _4^2\gt }}{4sin\theta cos\theta} \quad\quad[/math] and [math]\quad\quad \lt {v\prime w\prime}\gt =\Large\frac{{\lt u\prime_1^2\gt }-{\lt u\prime _2^2\gt }}{4sin\theta cos\theta}[/math]

where the triangle brackets represent the temporal means and the primes indicate temporal fluctuations. The rate [math]P[/math] of production of TKE in W m-3 is estimated from the product of the Reynolds stresses and the velocity shear according to:

[math]P = -\rho \left( \lt u\prime w\prime\gt \Large\frac{\partial u}{\partial z}\normalsize + \lt v\prime w\prime\gt \Large\frac{\partial v}{\partial z}\normalsize\right) [/math],

where [math]\rho[/math] is the water density and [math]z[/math] is the vertical coordinate. Using this method we can also estimate the value of the eddy viscosity, [math]N_z[/math], as:

[math] \Large\frac{\tau_x}{\rho}\normalsize = N_z \Large\frac{\partial u}{\partial z}\normalsize = \lt u\prime w\prime\gt \qquad [/math] and [math] \quad\quad \Large\frac{\tau_y}{\rho}\normalsize = N_z \Large\frac{\partial v}{\partial z}\normalsize = \lt v\prime w\prime\gt [/math],

where [math]\tau_x[/math] and[math]\tau_y[/math]are the eastward and northward components of stress. The method above is also referred to as the "variance method". For a more detailed explanation of the variance method, see Stacey et al. (1999[3]) and Rippeth et al. (2002[5]).

To estimate the TKE dissipation ([math]\epsilon[/math]) the structure function method is used. The method was first developed by meteorologist to estimate ε from radar measurements (Lhermitte, 1968[11]) and it has been applied to the marine environment, with promising results, by Wiles et al. (2006[10]). The method is based on the theory that a second order structure function [math]D(z,r)[/math] can be defined as:

[math] D(z,r)=\lt (v\prime(z)-v\prime(z+r))^2\gt [/math].

[math]D(z,r)[/math] is the mean-square of the along beam velocity fluctuation ([math]v’[/math]) difference between two points separated by a distance [math]r[/math]. Using the Taylor cascade theory to relate length scales and velocity scales to isotropic eddies we have:

[math] D(z,r)=C^2_v \epsilon ^{2/3} r^{2/3}[/math]

where [math]{C_v}^2[/math] is a constant between 2 and 2.2 for atmospheric studies. Here this assumption is used for marine studies, although it appears to underestimate the dissipation values.

Example of estimating turbulence

The variance method has been clearly validated by Howarth and Souza (2005[8]) and Souza and Howarth(2005[9]) and it has become a very popular technique to estimate turbulence characteristics in shelf seas and estuaries, so there are plenty examples of the use of ADCPs to estimate Reynolds stresses and turbulence production. Here an example will be shown from the Gulf of California, Mexico, which is one of the best data available.

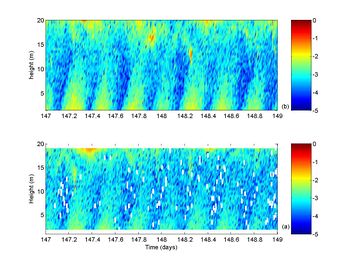
The data from the Gulf of California are plotted in Figure 2 with [math]\epsilon(a), P (b)[/math] and [math]N_z[/math]. As expected, the highest rate of TKE production is found near the bed with values decreasing about an order of magnitude between the bottom and 12 mab (Fig. 2b). The near-bed (~1.5 mab) maximum P is of the order of 10-2 W m-3 during both ebb and flood with minimum values at slack water of the order of 10-4 W m-3. The bottom production [math]P[/math] shows a quarter-diurnal periodicity as it is dependent on the current speed, i.e. there are two maxima of current speed per semi-diurnal tidal cycle. There is an apparent asymmetry between flood and ebb, with higher values of [math]P[/math] and greater extension up into the water column during ebb.

Estimates of eddy viscosity ([math]N_z[/math]) were calculated from hourly averages of Reynolds stresses and shear. These estimates of eddy viscosity (figure 3) show variability between 10-3 and 10-2 m2 s-1 in the bottom half of the water column, with maximum values around peak flow and low values around slack water. The mean eddy viscosity shows a typical profile with values slightly increasing from the bottom (~ 3 × 10-3 m2 s-1) to about 3.8 × 10-3 m2 s-1 at about 3 mab followed by a continuous decrease to near zero at 12 mab.

Figure 2 (a) Production (b) dissipation in W m-3
Figure 3 Time series of estimates of eddy viscosity

Estimation of turbulence using Acoustic Doppler Velocitymeters (ADVs)

The techniques to estimate turbulence parameters explained above are becoming common practice with ADCPs. However, nowadays the standard way to carry out turbulence measurements is by using Acoustic Doppler Velocimeters (ADV (R)). The ADV (R) follows a direct method of measuring the Reynolds stresses which involves rapid sampling of the three components of velocity in a small sampling volume, so that terms of the type [math]\lt u'w' \gt [/math] can be calculated directly from the covariance of [math]u[/math] and [math]w[/math]. This approach was pioneered by Bowden and Fairbairn (1956[12]), using electro-magnetic current meters. In this way not only the Reynolds stresses are obtained, but also the Turbulent Kinetic Energy (TKE) from the direct estimates of the variance of [math]u,v[/math], and [math]w[/math]. Hence:

[math] q^2=\frac{1}{2} \left( \lt u\prime^2\gt +\lt v\prime^2\gt +\lt w\prime^2\gt \right)[/math]

In recent years the use of Electromagnetic Current Meters (ECMs) has been substituted by using ADVs, which are simpler to use and can sample smaller water volumes, depending on frequency and brand. The ADVs used in these measurements were Sontek 5 MHz Ocean instruments, which have a volume sample of about 2 cm3 at sampling rates of about 25 Hz,. These instruments are highly accurate (long term error of the order of 3 × 10-6 m2 s-2) and have become the standard for boundary studies in the laboratory and field experiments.

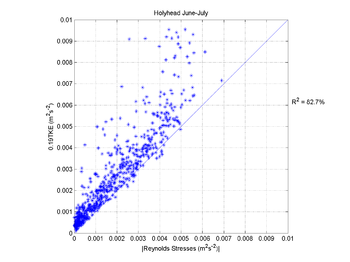
The advantage of having direct estimates of both TKE and Reynolds stresses is the possibility to look at relations between them. It is assumed that the Reynolds stresses are proportional to the TKE with a proportionality constant of 0.19; Figure 4 shows the plot of Reynolds stresses against 0.19 TKE, with the continuous line being the 1 to 1 value. The data do not fall on this line, but they are very close with the actual value of about 0.21.

Figure 4 TKE vs Reynolds stresses
Figure 5 Example of spectrum for w as measured by an ADV in Liverpool Bay, the Black line shows an almost -5/3 slope

The advantage of using ADVs is that we can use the inertial dissipation method to calculate TKE dissipation (ε). This method was first used in meteorology and was originally described by Deacon (1959[13]) and reviewed more recently by Huntley (1988[14]).

The inertial dissipation method involves the use of spectra of turbulent fluctuations and is based on the assumption that the wave numbers at which turbulence is produced are well separated from the wave number at which the TKE is dissipated by viscosity. This range of wave numbers between production and dissipation is known as the inertial subrange. In this range the flux of energy from high to low wave numbers must be equal to the dissipation rate (ε) if we assume that there are no local sources or sinks of TKE. Following Tennekes and Lumley (1972[15]) the three-dimensional inertial spectrum must be given by:

[math]E(k)\,=\alpha\,\epsilon\,^{2/3}k^{-5/3}\,[/math]

where [math]k[/math] is the wave number and [math]\alpha[/math] is the three-dimensional Kolmogorov constant. In practice we do not have estimates of the three-dimensional wave number spectrum, but one-dimensional spectra that are function of the along flow wave number [math]k_1[/math]. These one dimensional spectra [math]\phi_{ii}(k_1)[/math], where i=1,2,3, are the longitudinal transverse and vertical turbulence fluctuations. Hence:

[math]\phi_{ii} (k_1)= \alpha_i \epsilon^{2/3}k_1^{-5/3}[/math],

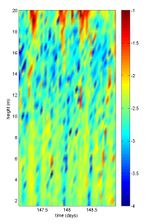
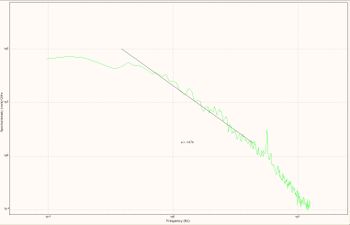
which is similar to the previous equation, using the correct Kolmogorov constant. In practice the vertical flow spectra are used, due to the fact that they are less contaminated by wave motion in the inertial subrange (Huntley, 1988[14]; Grant et al., 1984[16]). As data are usually collected as a time series of turbulence, we use Taylor’s frozen turbulence concept to relate the frequency spectrum (fig. 5) to wave number spectrum as follows:

[math] \phi_{ii}(k)=\Large\frac{\phi_{ii}(f)}{2\pi/ \lt u\gt } [/math].

This technique has recently been extended by Lorke and Wüest (2005[17]) to be used with ADCPs.

See also

Internal links

External links

Producers of popular instruments are:

References

  1. ↑ 1.0 1.1 Sontek, 2004. PC-ADP Read me first. Sonetek, San Diego, USA
  2. ↑ RDI, 1996. Acoustic Doppler Current Profiler Principles of operation a practical primer, RDI, San Diego, USA
  3. ↑ 3.0 3.1 3.2 Stacey, M.T., Monismith, S.G., Burau, J.R., 1999. Measurement of Reynolds stress profiles in unstratified tidal flow. Journal of Geophysic al Research 104 (C5), 10,933–10,949.
  4. ↑ Lu, Y., Lueck, R.G., 1999. Using a broadband ADCP in a tidal channel. Part II: turbulence. Journal of Atmospheric and Oceanic Technology 16, 1568–1579.
  5. ↑ 5.0 5.1 Rippeth, T.P., Williams, E., Simpson, J.H., 2002. Reynolds stress and turbulent energy production in a tidal channel. Journal of Physical Oceanography 32, 1242–1251.
  6. ↑ Souza, A.J., Alvarez, L.G., Dickey, T., 2004. Tidally induced turbulence and suspended sediment. Geophysical Research Letters 31, L20309, doi:10.1029/2004GLO21186.
  7. ↑ Williams, E., Simpson, J.H., 2004. Uncertainties in estimates of Reynolds stress and TKE production rate using the ADCP variance method. Journal of Atmospheric and Oceanic Technology 21 (3), 347–357.
  8. ↑ 8.0 8.1 Howarth, M.J. and A.J. Souza (2005) Reynolds stress observations in continental shelf seas.Deep Sea Res II, 52, 1075–1086.
  9. ↑ 9.0 9.1 Souza A.J. and M.J. Howarth, 2005. Estimates of Reynolds stress in a highly energetic shelf sea. Ocean Dynamics, 55, 490-498.
  10. ↑ 10.0 10.1 Wiles, P. J., T. P. Rippeth, J. H. Simpson, and P. J. Hendricks, 2006. A novel technique for measuring the rate of turbulent dissipation in the marine environment, Geophys. Res. Lett., 33, L21608, doi:10.1029/2006GL027050.
  11. ↑ Lhermitte, R. (1968), Turbulent air motion as observed by Doppler radar, paper presented at 13th Radar Meteorological Conference, Am. Meteorol. Soc., Montreal, Que., Canada.
  12. ↑ Bowden, K.F. and L.A. Fairbairn, Measurements of turbulent fluctuations and Reynolds stresses in a tidal current. Proc. Roy. Soc. London, Series A, 237, 422-438, 1956.
  13. ↑ Deacon, EL, 1959.The measurements of turbulent transfer in the lower atmosphere. Advances in Geophysiscs, 6, Acad. Press, 211-228.
  14. ↑ 14.0 14.1 Huntley, D.A. (feb 1988), A modified inertial dissipation method for estimating seabed stresses at low reynolds-numbers, with application to wave current boundary-layer measurements, Journal of physical oceanography, 18 (2): 339-346.
  15. ↑ Tennekes, H. and J.L. Lumley, 1972. A first Course in Turbulence, MIT Press, 300pp.
  16. ↑ Grant, W.D., A.J. Williams, III and S.M. Glenn, 1984. Bottom Stress estimates and their predictionon the Northern Continental Shelf during CODE-1: The importance of wave current interaction J. Phys. Oceanogr., 14, 506-527,
  17. ↑ Lorke A, Wuest A (Nov 2005), Application of coherent ADCP for turbulence measurements in the bottom boundary layer, Journal of atmospheric and ocean technology 22(11): 1821-1828
The main author of this article is Souza, Alex
Please note that others may also have edited the contents of this article.
Citation: Souza, Alex (2020): Currents and turbulence by acoustic methods. Available from http://www.coastalwiki.org/wiki/Currents_and_turbulence_by_acoustic_methods [accessed on 21-12-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Currents_and_turbulence_by_acoustic_methods&oldid=78287"