Ekman transport
Definition of Ekman transport:
Wind-driven water transport deflected by the Earth's rotation.
This is the common definition for Ekman transport, other definitions can be discussed in the article
|
Contents
Ekman spiral
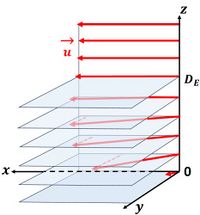
Due to the Earth’s rotation, ocean currents are deflected to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. This phenomenon is called Coriolis effect and explained in the article Coriolis acceleration. This means that currents driven by wind stress at the water surface do not follow the wind direction, but are deviated. The wind-driven water transport deflected by the Earth's rotation is called Ekman transport, named after the Swedish oceanographer Vagn Walfrid Ekman who first described this phenomenon[1]. The deflection angle of the current increases with depth, measured from the surface (Fig. 1). The veering of the current with depth depends on the intensity of the turbulent fluid motions in the water column, which can be captured in a so-called 'eddy viscosity' coefficient [math]K_z[/math]. Ekman transport is largely restricted to the ocean upper layer with thickness [math]D_E[/math], the so-called Ekman depth, which is of the order of 100 m. Although the currents associated with Ekman transport are small (typically less than 0.1 m/s), the large horizontal extent makes that the total amount of water transported can be huge, comparable to the transport of major ocean currents such as the Gulf Stream or the Kuroshio[2].
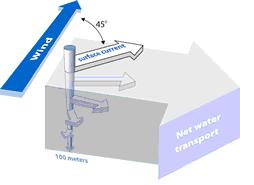
When surface waters are exposed to wind stress, they drag the deeper layers with them. Each layer of water is moved by friction from the shallower layer and each deeper layer moves more slowly than the layer above it. The direction of flow in each layer is deflected by the Earth's flow rotation. The resulting veering of the current is called the Ekman spiral. The deflection of the surface current has an angle of 45° (bending to the right, in the Northern Hemisphere). At the Ekman depth, the water flows in a direction opposite to the surface current. The depth-averaged net water transport is perpendicular (90°) to the wind direction and this is the effective direction of the Ekman transport. [3] Field observations show that the veering angles of the wind-driven current are in reality larger than predicted by the Ekman theory. The surface current lies more than the predicted 45° to the right of the wind, and the current amplitude decreases at a faster rate than it turns to the right, resulting in a flatter spiral than the theory predicts. These differences are due to processes not considered in the idealized Ekman model, for example stratification[4].
Consequences of Ekman transport
Ekman transport generates vertical water motions (upwelling or downwelling) through several mechanisms. Vertical water motions are of great significance for the ocean ecosystem. In the case of upwelling, they stimulate primary production by bringing nutrient-rich water from the deep ocean to the surface. In the case of downwelling, Ekman transport can contribute to carbon sequestration by downward transport of dissolved inorganic and organic carbon into deep ocean layers[5].
Vertical water transport is generated by zonal wind stress close to the equator, resulting from the varying strength of Ekman transport with latitude and the associated convergence or divergence of ocean currents (see Appendix). Diverging Ekman transport produces upwelling, also called Ekman suction. Converging Ekman transport produces downwelling, also called Ekman pumping. The trade winds at low latitudes and the westerlies at mid-latitudes generate a large-scale anticyclonic curl in the wind stress and corresponding large-scale anticyclonic gyres north and south of the equator, in both the Atlantic and the Pacific. Ekman transport converges in these gyres, generating large downwelling zones in the subtropical oceans[2].
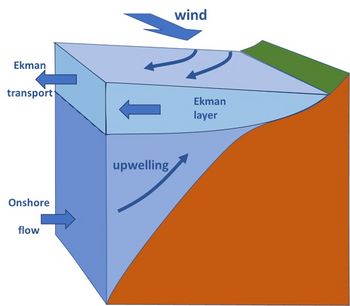
Upwelling and downwelling are particularly important at the shelf sea boundaries with the ocean. Coast-parallel winds drive surface waters offshore (if the coast is to the left, in the Northern Hemisphere) or onshore (if the coast is to the right). In the former case, the water surface dips towards the coast. The associated hydrostatic pressure gradient generates onshore transport of deep ocean water (beneath the Ekman layer) that then upwells to the surface (Fig. 2). In the latter case, a rise in the water surface towards the coast generates a hydrostatic pressure gradient that causes the downward flow of shelf water that is then transported offshore to the deep ocean.
Sverdrup transport
The anticyclonic curl of the wind stress produced by the veering of the wind stress from the low latitudes (trade winds) to the mid-latitudes (westerlies) also influences the geostrophic flow in the ocean interior (from the bottom of the Ekman layer to about one kilometer depth). It results in a meridional geostrophic flow directed to the equator, so-called Sverdrup transport, on both the Northern and Southern Hemispheres. These equatorward flows are compensated by a poleward return flow along the western continental boundaries, the Kuroshio, Gulf Stream, Brazil current and Agulhas, see Ocean circulation. A simple model of Sverdrup transport is shown in the Appendix. Observed transports agree well with predictions based on the wind field over large areas, primarily in the tropics and subtropics. Elsewhere, especially at higher latitudes and in boundary regions, Sverdrup balance does not accurately describe meridional geostrophic transports, possibly due to the increased importance of the barotropic flow, nonlinear dynamics, and topographic influence[6].
Ekman bottom layer
In the open ocean, the Ekman surface layer does not extend to the bottom. The currents in the ocean interior are largely geostrophic, with very small vertical shear (see the article Geostrophic flow). However, close to the bottom, the flow experiences the friction of the seabed. In this bottom boundary layer, called Ekman bottom layer, the velocity is also deflected, and tends while rotating to zero at the seabed (Fig. 3). Velocity veering is due to the Earth's rotation, just as in the Ekman surface layer. The Ekman transport in the bottom layer makes an angle to the geostrophic flow which is larger then the 90° angle of the Ekman transport in the surface layer, and the rotation is to the left instead of to the right. The Ekman transport in the bottom layer contributes to shelf sea exchange with the ocean by crossing isobaths. Ekman transport in the bottom layer can also contribute to vertical water motion depending on the geostrophic flow pattern. Upwelling occurs where geostrophic flows form a cyclonic gyre and downwelling in the opposite case (see the Appendix).
Appendix: Mathematical derivations
Ekman transport
The ocean response to a surface wind stress [math]\vec{\tau}(z=0) = \vec{\tau}_w[/math] on a rotating Earth follows from the momentum balance equations (see Coriolis acceleration)
[math]\Large\frac{1}{\rho}\frac{\partial \tau^{(x)}}{\partial z}\normalsize = - f \, v \, \qquad (1)[/math]
[math] \Large\frac{1}{\rho}\frac{\partial \tau^{(y)}}{\partial z}\normalsize = f \, u . \qquad (2)[/math]
The Coriolis parameter [math]f[/math] is given by [math]f=2 \Omega \sin \phi[/math], where [math]\Omega \approx 7.29211^{−5} \, s^{−1}[/math] is the radial earth rotation frequency and [math]\phi[/math] the elevation radian angle indicating latitude.
Meaning of the other symbols:
[math]x, \, y\,=[/math] spatial coordinates, along the horizontal Cartesian [math]x[/math] and [math]y[/math] axes
[math]z=[/math] coordinate along the vertical axis (upwards positive, water surface at [math]z=0[/math] )
[math]u(z),\, v(z) =[/math] components of the current velocity [math]\vec{u}(z)[/math] along the [math]x[/math] and [math]y[/math] axis, respectively
[math]\rho=[/math] seawater density
[math]\tau^{(x)}(z), \, \tau^{(y)}(z) =[/math] components of the shear stress along the [math]x[/math] and [math]y[/math] axis, respectively
The equations (1) are a simplified form of the momentum balance following the assumptions of (a) steady flow (no time dependence), (b) uniform seawater density and (c) no sea surface slope (i.e. no piling up of seawater against boundaries).
We assume that the wind stress acts in the [math]x[/math] direction, [math]\tau^{(x)}(z=0) = \tau_w \, , \, \tau^{(y)}(z=0)=0[/math]. The wind shear stress is related to the wind speed [math]V[/math] (usually taken at 10 m above the water surface) and the roughness of the water surface. It can be estimated from the empirical formula [math]\tau_w = \rho_{air} C_D V^2[/math], with [math]\rho_{air} \approx 1.2 \; kg \, m^{-3}[/math] and [math]C_D \approx (1-2) \, . \, 10^{-3}[/math].
Integration of Eq. (1) over the depth gives the net mass transports [math]M^{(x)} \, , \, M^{(y)}[/math] in the [math]x[/math] and [math]y[/math] directions respectively:
[math]M^{(x)} \approx \int_{-\infty}^0 u dz = 0 \, , \, M^{(y)} \approx \int_{-\infty}^0 v dz = - \Large\frac{\tau_w}{\rho f}\normalsize. \qquad (3)[/math]
This expression shows that wind stress along the [math]x[/math] direction produces a net mass transport, the so-called Ekman transport, to the right of the wind stress (in the negative [math]y[/math] direction). It should be noted that Ekman transport does not depend on the rate of momentum diffusion in the vertical or on effects of stratification.
Ekman spiral
We will adopt a further simplification by assuming that shear stresses are related to the local velocity gradient with constant eddy viscosity [math]K_z[/math] (which is typically in the range 0.01-0.05 m2/s; it should be noted that a constant eddy viscosity is seldom observed in field situations). The corresponding formula is
[math]\vec{\tau}(z) = \rho \, K_z \, \Large\frac{\partial \vec{u}}{\partial z} \normalsize . \qquad (4)[/math]
The momentum balance equations (1, 2) then become
[math] K_z \Large\frac{\partial^2 u}{\partial z^2}\normalsize = - f \, v \, , \quad K_z \Large\frac{\partial^2 v}{\partial z^2}\normalsize = f \, u . \qquad (5)[/math]
With the assumption of great depth, the solution of these linear equations take the form
[math]u(z) = \Re [a \exp(\kappa z)] \, , \; v(z) = \Re [b \exp(\kappa z)] , \quad \Re[\kappa] \gt 0 , \qquad (6)[/math]
where [math]a, b, \kappa[/math] are complex numbers. Solving [math]\kappa[/math] by substitution of Eq. (6) in Eq. (5) gives
[math]a = \pm i b \, , \quad \kappa = \Large\frac{\pi \pm i \pi}{D_E}\normalsize , \qquad (7)[/math]
where [math]D_E[/math] is the Ekman depth given by [math]\; D_E = \pi \sqrt{\large\frac{2 K_z}{|f|}\normalsize} . \qquad (8)[/math]
The shear stress near the water surface [math]\rho K_z \Large\frac{d \vec{u}}{dz}\normalsize (z=0)[/math] is equal to the wind stress [math]\vec{\tau}_w[/math] along the [math]x[/math] axis. This condition yields
[math]a = u_0 e^{-i \pi /4} \, , \quad u_0 = \Large\frac{\sqrt{2} \pi \tau_w}{\rho |f| D_E}\normalsize \qquad (9)[/math]
and in the Northern Hemisphere,
[math]u(z) = u_0 \cos \Big(-\large\frac{\pi}{4}\normalsize + \large\frac{\pi z}{D_E}\normalsize \Big) \exp\Big(\large\frac{\pi z}{D_E}\normalsize\Big) \, , \; v(z) = u_0 \sin \Big(-\large\frac{\pi}{4}\normalsize + \large\frac{\pi z}{D_E}\normalsize \Big) \exp\Big(\large\frac{\pi z}{D_E}\normalsize\Big) . \qquad (10)[/math]
This expression represents the Ekman spiral shown in Fig. 1.
Ekman pumping
Ekman transport generates a vertical velocity [math]w(z)[/math] through the continuity equation
[math]\Large\frac{\partial w}{\partial z}\normalsize = - \Big( \Large\frac{\partial u}{\partial x}\normalsize + \Large\frac{\partial v}{\partial y}\normalsize \Big) . \qquad (11)[/math]
We use the convention here that the [math]x[/math] axis is oriented W-E and the [math]y[/math] axis S-N. In this case [math]df/dx= 0[/math] and [math]df/dy = \beta, \; \beta = 2 \Omega \cos \phi /R[/math], where [math]R[/math] is the Earth's radius.
Now we derive Eq. (2) with respect to [math]x[/math] and Eq. (1) with respect to [math]y[/math] and subtract the results. This yields
[math] \Large\frac{1}{\rho}\frac{\partial}{\partial z} \Big( \frac{\partial \tau^{(y)}}{\partial x} - \frac{\partial \tau^{(x)}}{\partial y}\normalsize \Big) - v \beta = \Large\frac{1}{\rho}\frac{\partial}{\partial z} \Big( \frac{\partial \tau^{(y)}}{\partial x} - \frac{\partial \tau^{(x)}}{\partial y} \normalsize \Big) + \Large\frac{\beta}{\rho f} \frac{\partial \tau^{(x)}}{\partial z} \normalsize= f \Big( \Large\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \normalsize \Big) = - f \Large\frac{\partial w}{\partial z}\normalsize . \qquad (12)[/math]
This equation (the 2nd and 4th members) can be integrated from the Ekman depth [math]-D_E[/math] to the surface. Neglecting shear stresses at the Ekman depth with respect to the surface shear stresses, the following estimate for the vertical velocity [math]w_E[/math] at the Ekman depth is obtained:
[math]w_E = \Large \frac{1}{\rho f} \Big( \frac{\partial}{\partial x}\normalsize \tau_w^{(y)} - \Large\frac{\partial}{\partial y}\normalsize \tau_w^{(x)} \Big) + \Large\frac{\beta}{\rho f^2}\normalsize \tau_w^{(x)} . \qquad (13)[/math]
This expression has a singularity at the equator where [math]f=0[/math], which is due to the model simplifications. The formula (13) shows that the Ekman transport mechanism can generate substantial vertical water motions near the equator. The subtropical trade winds which are oriented E-W ([math]\tau_w^{(x)} \lt 0[/math]) increase towards the equator ([math]f^{-1} \, \partial \tau_w^{(x)} / \partial y [/math] > 0). This produces downwelling currents ([math]w_E \lt 0[/math]) in the surface Ekman layer of the subtropical ocean. The transition zones from the low-latitude trade winds to the westerlies at higher latitudes can be considered large-scale anticyclonic gyres with corresponding downwelling currents[2], see Ocean circulation.
Sverdrup transport
Sverdrup transport is another consequence of the changing Coriolis acceleration with latitude. We assume that the flow in the interior of the ocean water column (below the Ekman layer) is geostrophic (see Geostrophic flow) with horizontal components [math]U, V[/math] along the [math]x, y[/math] axes,
[math]U = - \Large\frac{1}{\rho f}\frac{\partial p}{\partial y}\normalsize \, , \quad V = \Large\frac{1}{\rho f}\frac{\partial p}{\partial x}\normalsize . [/math]
Substitution of [math]u=U[/math] and [math]v=V[/math] in the continuity equation (11) gives [math]\Large\frac{\partial w}{\partial z}\normalsize = - \Large\frac{1}{\rho}\frac{\partial p}{\partial x}\frac{\partial}{\partial y}\big( \frac{1}{f} \big)\normalsize = \Large\frac{\beta}{f}\normalsize V . [/math]
By integrating this equation over the geostrophic interior of the ocean water column (depth [math]D[/math]) to the lower boundary of the Ekman layer we find
[math]M_{Sv} = \int_{-D}^{-D_E} V \, dz = \Large\frac{f}{\beta}\normalsize w_E = \Large \frac{1}{\rho \beta} \Big( \frac{\partial}{\partial x}\normalsize \tau_w^{(y)} - \Large\frac{\partial}{\partial y}\normalsize \tau_w^{(x)} \Big) + \Large\frac{1}{\rho f}\normalsize \tau_w^{(x)} . \qquad (14)[/math]
The Sverdrup transport [math]M_{Sv}[/math] is a meridional flow in the upper part of the ocean produced by the large-scale curl of the wind stress.
Ekman bottom layer
We assume a geostrophic current [math]\vec{U} = (U, V, 0)[/math] which is uniform in the vertical (no depth dependence), see Geostrophic flow. However, in a layer close to the bottom, the Ekman bottom layer, this current will experience the friction of the seabed. It will therefore be rectified by a current [math]\vec{u}' = (u', v', w')[/math] such that [math]\vec{u} = \vec{U} + \vec{u}' =0[/math] at the seabed. The [math]z[/math] axis in now chosen such that [math]z=0[/math] at the seabed.
The equations of motion are
[math]\Large\frac{1}{\rho}\frac{\partial \tau^{(x)}}{\partial z}\normalsize = - f \, v' \, , \quad \Large\frac{1}{\rho}\frac{\partial \tau^{(y)}}{\partial z}\normalsize = f \, u' . \qquad (14)[/math]
We assume that in the Ekman bottom layer the shear stress can be represented by a constant eddy viscosity constant [math]K_z[/math], thus [math]\vec{\tau}(z) = \rho \, K_z \, \Large\frac{\partial \vec{u'}}{\partial z} \normalsize . [/math] Solving the equations (4) with the boundary condition [math]\vec{u}'=(-U,-V,0)[/math] at [math]z=0[/math] and [math]\vec{u}'=0[/math] for [math]z \rightarrow \infty[/math] gives (Northern Hemisphere, Fig. 3)
[math]u(z) = U + u'(z) = U \, \Bigl[1 - \cos \big( \large\frac{\pi z}{D_E}\normalsize \big) \exp\big(\large\frac{-\pi z}{D_E}\normalsize\big) \Bigr] - V \sin \big(\large\frac{\pi z}{D_E}\normalsize \big) \exp\Big(\large\frac{-\pi z}{D_E}\normalsize\big) \, , \; v(z) = V + v'(z) = U \sin \big(\large\frac{\pi z}{D_E}\normalsize \big) \exp\Big(\large\frac{-\pi z}{D_E}\normalsize\big) + V \, \Bigl[1 - \cos \big( \large\frac{\pi z}{D_E}\normalsize \big) \exp\big(\large\frac{-\pi z}{D_E}\normalsize\big) \Bigr], \qquad (15)[/math]
with the same formula (8) for the thickness [math]D_E[/math] of the Ekman bottom layer, [math]\; D_E = \pi \sqrt{\large\frac{2 K_z}{|f|}\normalsize} . [/math]
The velocity is veering in the Ekman bottom layer, as in the Ekman surface layer. The Ekman mass transport in the Ekman bottom layer is given by
[math]M^{(x)} = \int_0^{D_E} u'(z) dz \approx - \large\frac{D_E}{2 \pi}\normalsize (U+V) \, , \; M^{(y)} = \int_0^{D_E} v'(z) dz \approx \large\frac{D_E}{2 \pi}\normalsize (U-V) . \qquad (16)[/math]
The Ekman mass transport in the bottom layer is oriented 135° to the left of the geostrophic flow. The vertical flow [math]w[/math] at [math]z=D_E[/math] can be derived from the continuity equation (11), using Eq. (16) and the geostrophic relation [math]\Large \frac{\partial U}{\partial x}\normalsize + \Large \frac{\partial V}{\partial y}\normalsize = 0[/math] ,
[math]w(z=D_E) = - \int_0^{D_E} \Big( \Large \frac{\partial u}{\partial x}\normalsize + \Large \frac{\partial v}{\partial y}\normalsize \Big) \, dz = - \int_0^{D_E} \Big( \Large \frac{\partial u'}{\partial x}\normalsize + \Large \frac{\partial v'}{\partial y}\normalsize \Big) \, dz = \large\frac{D_E \, U}{2 \pi}\normalsize \Big( \Large \frac{\partial V}{\partial x}\normalsize - \Large \frac{\partial U}{\partial y}\normalsize \Big) . \qquad (17)[/math]
Cyclonic vorticity of the geostrophic flow produces upwelling and anticyclonic geostrophic flow downwelling.
Related articles
References
- ↑ Ekman, V.W. 1905. On the influence of the Earth’s rotation on ocean-currents. Arch. Math. Astron. Phys. 2: 1-52
- ↑ 2.0 2.1 2.2 Chereskin, T.K. and Price, J.F. 2001. Ekman transport and pumping. Encyclopedia of Ocean Science, vol. 2, p. 809-815. Elsevier
- ↑ Pinet P.R. 1998.Invitation to Oceanography. Jones and Barlett Publishers. p. 508
- ↑ Price, J.F. and Sundermeyer, M.A. 1999. Stratified Ekman layers. J. Geophys. Res. 104: 20.467-20.494
- ↑ Liao, E., Resplandy, L., Liu, J. and Bowman, K. W. 2020. Amplification of the ocean carbon sink during El Niños: Role of poleward Ekman transport and influence on atmospheric CO2. Global Biogeochemical Cycles 34, e2020GB006574
- ↑ Gray, A.R. and Riser, S.C. 2014. A Global Analysis of Sverdrup Balance Using Absolute Geostrophic Velocities from Argo. J. Phys. Oceanography 142: 1213-1229
Please note that others may also have edited the contents of this article.
|
