Swash

From Coastal Wiki
Jump to: navigation, search
Definition of Swash:
Propagation of thin sheets of seawater up and down the beach, after the collapse of waves on the beach face. Swash is the decelerating uprush phase and backwash is the accelerating downrush phase.
This is the common definition for Swash, other definitions can be discussed in the article


Fig. 1. Swash on a reflective beach, Avoca Beach, NSW, Australia. In the background, a wave collapses on the beach; the swash uprush reaches the top of the beach berm. Photo credit: Dr Hannah Power, University of Newcastle, NSW, Australia.

Swash zone

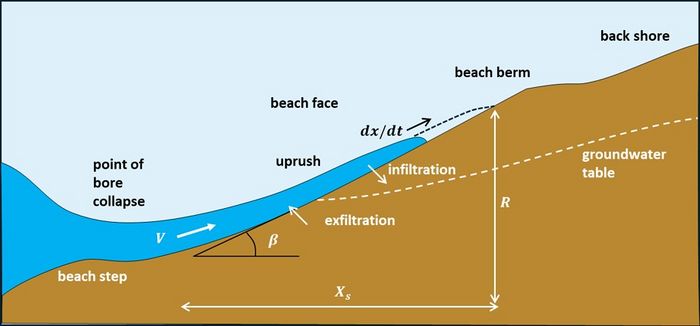
When incident waves collapse on the beach face, a thin layer of seawater rushes up the beach in the swash zone, located between the surf zone and the dry beach (Fig. 1). The swash zone typically coincides with the steeper part of the beach—especially on coarse-grained beaches—and is often bounded landward by a beach berm. The maximum elevation reached by individual swash events varies greatly. Numerous empirical formulas have been developed for the maximum run-up, commonly defined as the level exceeded by only 2% of swash events (see Wave run-up). Swash motion forms a crucial link between hydrosedimentary processes in the surf zone and the morphology (sand volume and shape) of the backshore.


Swash motion can be quite strong. Maximum uprush velocities up to 3 m/s have been measured on steep sandy foreshores and up to 2 m/s on gently sloping foreshores, while backwash velocities can attain more than 2 m/s[1]. Uprush suspended sediment concentrations on steep and dissipative beaches can approach or exceed 100 g/l. The net sediment transport of a single swash event can cause fluctuations in beach level (accretion or erosion) by up to several centimeters. The net bed level change over an entire tidal cycle is often not much larger (less than an order of magnitude) than the change by individual swash events[2].

While easily observed and experienced by anyone walking along the beach, measuring the hydrodynamic characteristics of swash motion is not easy at all because of its small scale and highly unsteady nature. Swash motion is driven by waves collapsing on the beach which supply initial momentum to the wave uprush along with an amount of suspended sediment. This complex boundary condition, given the irregular character of the incident wave field, is not the only challenge for modelling the swash dynamics. The up and down flowing fluid sheets induce pore water pressure gradients with alternating upward and downward seepage that promotes destabilization of the sediment bed and transport of suspended liquefied sediments[3][4]. The capability of process-based models to simulate these fine-scale processes is very limited. The contribution of swash motion to maximum water uprush and to beach accretion and erosion processes is therefore mainly based on empirical relationships. General trends can be fairly well described by these relationships, but field data are widely scattered around these trends. See the article Swash zone dynamics for a more detailed discussion.

On dissipative coasts swash processes are dominated by infragravity waves.

The formation of beach cusps is intimately linked to the swash process. This is dealt with in the article Beach cusps.

Swash sedimentation and erosion

Sediment suspended in the surf zone and eroded from the lower beach face is deposited on the upper beach face, where uprush velocities are small. Deposition is enhanced by infiltration, particularly on coarse-sediment beaches with average grain size [math]d_{50}[/math] larger than 1 mm. Infiltration has two opposing effects on bed shear stress: a decrease due to reduction of the flow volume and an increase due to thinning of the boundary layer.

After reaching the highest point on the beach face, the water retreats downslope in a very thin layer. This so-called downrush or backwash transports sediment from the upper to the lower beach face. The backwash period is generally longer than the uprush period and its velocity is lower. During the late stage of the backwash, a thick sheet-flow layer develops, which rapidly diminishes after the arrival of the next incident bore[5].

Exfiltration near the shoreline also has two opposing effects: thickening of the boundary layer and a related decrease in bed shear stress, versus bed destabilization through liquefaction of the bed sediment layer[6]. Laboratory experiments show that bed shear stresses are similar for impermeable and permeable beaches composed of fine or medium sand, whereas higher bed shear stresses occur on permeable gravel beaches[7]. Field observations suggest that the net effect of infiltration and exfiltration depends on grain size. For medium sediment, infiltration decreases the uprush sediment flux ([math]\approx -10%[/math]) and increases the downrush sediment flux ([math]\approx 5%[/math]); for coarse sediment the effect is reversed.


Fig. 2. Schematic representation of swash uprush on the beach face. The vertical scale is strongly exaggerated. The swash excursion [math]X_s[/math] extends landward from the location where the incident wave bore collapses.


Entrainment of the upper bed layer (1–2 cm) supplies sediment to both the uprush and backwash fluxes[8][9]. Sediment suspended in the wave bore collapsing on the beach also contributes substantially to the sediment load of the swash uprush[10].

Part of the sediment deposited by the uprush is subsequently remobilized by the backwash. High sediment concentrations and fluxes are typically observed at the beginning of the uprush and during the final stage of the backwash. The highest deposits may remain unaffected due to scour lag: by the time the backwash reaches velocities sufficient for remobilization, it has already retreated below these deposits. The highest uprush deposits form a beach berm (Fig. 2). During extreme storms, the berm may evolve into a ridge on the upper beach[11].

Field experiments by Masselink et al. (2009[9]) showed that net accretion or erosion can vary greatly between successive individual swash events. Individual swash events typically produce either net onshore or net offshore transport; partial cancellation occurs only when averaged over many events. A single swash event can contribute substantially to the total accretion or erosion occurring over an entire tidal cycle[12]. Significant accretion occurs when breaking wave bores transport large suspended sediment loads from the inner surf zone. Conversely, when swash is pushed high up the beach by the combined uprush of short waves and a long infragravity wave, the resulting strong backwash can produce major erosion[10]. These dynamics highlight the challenge of accurately simulating swash-driven accretion or erosion using process-based numerical models.

Swash zone equilibrium slope

Dominance of onshore or offshore sediment transport is strongly influenced by swash–swash interaction, particularly the collision between the backwash flow and the following uprush. Holland and Puleo (2001[13]) observed that net offshore sediment transport occurs when the backwash is not intercepted by the next uprush. This situation arises when the average wave period [math]T[/math] exceeds the average swash period [math]T_s[/math]. Conversely, net onshore transport prevails when the backwash collides with the subsequent uprush.

Based on these observations, these authors proposed a mechanism of negative morphodynamic feedback. If initially the average wave period [math]T[/math] exceeds the swash period [math]T_s[/math], offshore sediment transport causes beach lowering and a reduction of the beach-face slope. According to the ballistic model (Eq. A4), a decrease in beach slope increases the uprush period. Over time, the swash period may therefore exceed the average wave period [math]T[/math], causing the backwash to collide with the following uprush. This interaction reduces offshore transport by the backwash, resulting in net beach accretion. As the beach face accretes, the slope increases and the swash period decreases. An equilibrium beach-face slope may then develop for which [math]T_s[/math] and [math]T[/math] are of similar duration.

This morphodynamic feedback model is likely oversimplified. Observations indicate that swash periods are generally larger—by a factor of 1–3—than the average period of incident short waves, but shorter than the typical period of infragravity waves[13][10]. Moreover, under irregular wave conditions, individual swash events exhibit large variability. This is particularly evident on dissipative coasts, where wave amplitudes within wave groups are strongly modulated (see Infragravity waves). In addition, long-term beach equilibrium is not governed by swash processes alone, but also by surf-zone processes (wave breaking on the beach), especially during storm conditions[14].

Sediment grain size is another important factor influencing beach slope because swash uprush and backwash depend on infiltration and exfiltration within the beach sediment. Coarse sediment settles more readily at the end of the uprush than fine sediment, while greater infiltration in coarse material reduces the surface backwash flow and the associated downslope sediment transport. Achieving equilibrium between uprush and backwash sediment transport therefore requires a steeper beach slope. Consequently, coarse-grained beaches (such as gravel beaches) typically exhibit steeper slopes than fine- or medium-grained sandy beaches[15].

The relative swash period [math]T_s/T[/math] is larger on gently sloping dissipative beaches than on steep reflective beaches. On gently sloping beaches, offshore sand transport by the backwash is more likely to be reduced by early collision with the following uprush. This favors onshore sand transport by swash over offshore transport, as discussed above. Alsina et al. (2012[16]) provide evidence from flume experiments that artificially reducing the beach-face slope and increasing surface roughness can help counteract beach erosion and the offshore migration of nearshore sandbars. The application of this principle—adjusting the beach profile to stimulate accretion—is discussed in the article Beach scraping.

Infragravity swash

On gently sloping dissipative beaches incident short waves lose most of their energy by breaking in the surf zone [17]. Near the shoreline, only the longest waves survive, the so-called subharmonic or infragravity waves. Infragravity waves arise mainly from nonlinear interactions between short waves with different wavelengths and frequencies [18], see the article Infragravity waves. They carry only a small part of the wave energy on the lower shoreface (typically of the order of 1[math]\%[/math] or less), but their relative importance increases strongly in the surf zone. Infragravity waves dominate the swash motion on dissipative beaches. Empirical formulas for run-up of infragravity waves are given in the article Wave run-up.

While there is strong evidence that short-wave swash stimulates beach accretion, this is less clear for infragravity swash. Observations point to a net offshore directed transport by infragravity swash, especially in the seaward part of the swash zone. However, reliable models for simulating the complicated infragravity morphodynamics in the surf zone are not yet available [19].


Appendix: Ballistic swash model

In the case of monochromatic non-breaking incident waves (usually infragravity waves), the frictionless cross-shore vertical run-up [math]R[/math] on a beach with constant slope [math]\beta[/math] can be determined analytically, see the article Waves on a sloping bed. Such non-broken waves are reflected at the shoreline and form with the incident waves a pattern of standing waves. In the case of oblique wave incidence, these reflected waves can for a pattern of edge waves.

Here we consider the more usual case of dissipative or partially reflective beaches, where incident waves collapse on the beach face and rush up as a bore, see Fig. 2. The velocity [math]V[/math] of a collapsing wave front can be estimated from the bore formula[20] [math]\; V=2\sqrt{gD_0} \, ,[/math] where [math]D_0[/math] is the height of the collapsing wave (see Dam break flow). This assumes that all the energy of the collapsing wave is transferred to the uprush; the actual uprush velocity is generally somewhat lower.

Swash motion can be described with reasonable accuracy with a simple model based on ballistic theory[21][22]. A short introduction to the ballistic model is given below.

The horizontal position of the bore front is described by the trajectory [math]x(t)[/math] up and down the beach (Fig. 2). The time [math]t=0[/math] corresponds to the wave collapse, that generates at [math]x=0[/math] a bore with speed [math] dx/dt = V \approx 2\sqrt{gD_0}[/math]. If friction and infiltration are neglected, the trajectory [math]x(t)[/math] follows the ballistic equation

[math]\Large\frac{d^2 x}{dt^2}\normalsize = - g \beta \, , \quad x(t) = - \large\frac{1}{2}\normalsize g \beta t^2 + V\, t \, , \qquad (A1)[/math]

where [math]\beta[/math] is the slope of the beach face ([math]\beta \lt \lt 1[/math]). At the end of the uprush, [math]dx/dt=0[/math]. The uprush duration is thus given by [math]T_u \approx V / g \beta [/math]. In the frictionless case, the uprush duration [math]T_u[/math] and backwash duration [math]T_b[/math] are equal; the swash period [math]T_s = T_u+T_b[/math] is thus about twice the uprush duration. The horizontal run-up is given by [math]X_s = \large\frac{1}{2}\normalsize g \beta T_u^2 = \Large\frac{V^2 }{2g \beta}\normalsize = \Large\frac{2 D_0}{\beta}\normalsize[/math] and the vertical run-up by [math]R = \beta X_s = \large\frac{1}{2}\normalsize g \beta^2 T_u^2 = 2 D_0 \, . \qquad (A2)[/math].

The uprush loses energy by turbulent overturning at the bore front and by bed friction behind the front [23]. The velocities in the boundary layer of uprush and backwash have approximately a logarithmic profile with a friction coefficient of the order of [math]c_D \approx 0.005-0.02[/math] for a sandy beach[24][25][7][26]. The friction coefficient strongly depends on the sediment grainsize and it can vary during uprush and backwash.

A more accurate expression is found for the run-up by including a quadratic friction term in the ballistic equation (A1),

[math]\Large\frac{d^2 x}{dt^2}\normalsize = - g \beta - \Large\frac{c_D}{D} \big( \frac{dx}{dt}\normalsize \big)^2 \, . \qquad (A3)[/math]

This nonlinear equation can be solved analytically (by separation of variables), if the thickness [math]D[/math] of the bore and the friction coefficient are assumed constant in space and time. The solutions for the uprush period [math]T_u[/math] and the run-up [math]R[/math] are [21]

[math]T_u = \sqrt{ \Large\frac{D}{g \beta c_D}\normalsize} \tan^{-1} K , \quad R = - \Large\frac{\beta D}{c_D}\normalsize \ln (\cos(\tan^{-1} K) ) , \quad K = 2 \sqrt{\Large\frac{c_D D_0}{\beta D}\normalsize} \, . \qquad (A4) [/math]

With [math]c_D=[/math]0.025, a beach slope [math]\beta=[/math] 0.1, and with initial and average bore heights [math]D_0=[/math]0.5 m and [math]D=[/math]0.1 m, respectively, the friction reduces the uprush period [math]T_u[/math] from 4.5 s to 2.3 s and the run-up [math]R[/math] from 1 m to 0.36 m. For strong friction and gentle slopes (dissipative beaches), [math]K[/math] is generally much larger than 1 and we can approximate [math]\tan^{-1} K \approx \pi /2 - \epsilon[/math] with [math]\epsilon \lt \lt 1[/math]. The uprush period [math]T_u[/math] and run-up [math]R[/math] are then related by

[math]R \approx - \Large\frac{4 \ln \epsilon}{\pi^2 }\normalsize g \beta^2 T_u^2 \, . \qquad (A5) [/math]

This relationship is similar to that of the frictionless case (Eq. A2), apart from much shorter uprush times [math]T_u[/math]. The factor [math]- \ln \epsilon[/math] has values typically between 1 and 1.5. Experiments show that the duration of backwash [math]T_b[/math] is longer than the duration [math]T_u[/math] of uprush by 20-40[math]\%[/math] [13][27].

The run-up Eq. (A1) is related to the bore thickness estimates [math]D_0[/math] and [math]D(x,t)[/math], which depend on the height and period of the incident waves and on wave dissipation in the surf zone. Because no theoretical expression is available, empirical relationships for [math]R[/math] are used in practice, see Wave run-up.

Swash saturation and run-up limit
Laboratory and field observations show that the run-up [math]R[/math] is bound to a maximum value for high wave heights ([math]H[/math] of the order of 5 m or more). This is called 'swash saturation'. This can be due to wave breaking in the surf zone or breaking of infragravity waves on the beach. Another limit can result from the collision of the uprush with the preceding backwash[10]. Collision occurs when the swash period [math]T_s[/math] is longer than the period [math]T[/math] of the incident waves. Assuming that the uprush period [math]T_u[/math] and the downrush period [math]T_b[/math] are of similar order, then the backwash collision saturation criterium is [math]2 T_u \lt T[/math]. This implies for the maximum run-up (uprush height) a saturation limit [math]R_s[/math], according to the frictionless ballistic model (Eq. A2), [math]\qquad R \lt R_s \approx \large\frac{1}{8}\normalsize g \beta^2 T^2 \, . \qquad (1)[/math]



Related articles

Swash zone dynamics
Beach groundwater
Wave run-up
Wave breaking
Waves on a sloping bed
Beach cusps
Breaker index
Dam break flow


References

  1. ↑ Houser, C. and Barrett, G. 2010. Divergent behavior of the swash zone in response to different foreshore slopes and nearshore states. Mar. Geol. 271: 106–118
  2. ↑ Puleo, J.A., Lanckriet, T. and Blenkinsopp, C. 2014. Bed level fluctuations in the inner surf and swash zone of a dissipative beach. Mar. Geol. 349: 99–112
  3. ↑ Horn, D.P. 2002. Beach groundwater dynamics. Geomorphology 48: 121-146
  4. ↑ Kranenborg, J.W.M., Pauli, T., Jacobsen, N.G., van der Werf, J.J., Dionisio Antonio, S., Campmans, G.H.P., Reniers, A.J.H.M. and Hulscher, S.J.M.H. 2023. Measurements and modeling of pore-pressure gradients in the swash zone under large-scale laboratory bichromatic waves. Journal of Geophysical Research: Oceans 128, e2022JC019577
  5. ↑ Alsina, J.M., van der Zanden, J., Caceres, I. and Ribberink, J.S. 2018. The influence of wave groups and wave-swash interactions on sediment transport and bed evolution in the swash zone. Coast. Eng. 140: 23–42
  6. ↑ Butt, T., Russell, P. and Turner, I. 2001. The influence of swash infiltration-exfiltration on beach face sediment transport: onshore or offshore? Coastal Eng. 42: 35–52
  7. ↑ 7.0 7.1 Kikkert, G.A., Pokrajac, D., O'Donoghue, T. and Steenhauer, K. 2013. Experimental study of bore-driven swash hydrodynamics on permeable rough slopes. Coastal Eng. 79: 42-56
  8. ↑ Miles, J., Butt, T. and Russell, P. 2006. Swash zone sediment dynamics: A comparison of a dissipative and an intermediate beach. Mar. Geol. 231: 181–200
  9. ↑ 9.0 9.1 Masselink, G., Russell, P., Turner, I. and Blenkinsopp, C. 2009. Net sediment transport and morphological change in the swash zone of a high-energy sandy beach from swash event to tidal cycle time scales. Marine Geol. 267: 18–35
  10. ↑ 10.0 10.1 10.2 10.3 Brocchini, M. and Baldock, T.E. 2008. Recent advances in modeling swash zone dynamics: influence of surf-swash interaction on nearshore hydrodynamics and morphodynamics. Rev. Geophys. 46: 1–21
  11. ↑ Bendixen, M., Clemmensen, L.B. and Kroon, A. 2013. Sandy berm and beach-ridge formation in relation to extreme sea-levels: A Danish example in a micro-tidal environment. Marine Geol. 344: 53–64
  12. ↑ Blenkinsopp, C.E., Turner, I.L., Masselink, G. and Russell, P.E. 2011. Swash zone sediment fluxes: Field observations. Coastal Engineering 58: 28–44
  13. ↑ 13.0 13.1 13.2 Holland, K.T. and Puleo, J.A. 2001. Variable swash motions associated with foreshore profile change. J. Geophys. Res. 106: 4613–4623 Cite error: Invalid <ref> tag; name "HP" defined multiple times with different content
  14. ↑ Masselink, G. and Puleo, J.A. 2006. Swash-zone morphodynamics. Cont. Shelf Res. 26: 661–680
  15. ↑ Bujan, N., Cox, R. and Masselink, G. 2019. From fine sand to boulders: Examining the relationship between beach-face slope and sediment size. Marine Geology 417, 106012
  16. ↑ Alsina, J.M., Cáceres, I., Brocchini, M. and Baldock, T.E. 2012. An experimental study on sediment transport and bed evolution under different swash zone morphological conditions. Coast. Eng. 68: 31–43
  17. ↑ Ruessink, B.G. 1998. Bound and free infragravity waves in the nearshore zone under breaking and nonbreaking conditions. J. Geophys. Res. 103: 12,795-12,805
  18. ↑ Hasselmann, K. On the nonlinear energy transfer in a gravity-wave spectrum, part 1. General theory. J. Fluid Mech. 12: 481-500
  19. ↑ Elfrink, B. and Baldock, T. 2002. Hydrodynamics and sediment transport in the swash zone:a review and perspectives. Coastal Eng. 45: 149-167
  20. ↑ Ritter, A. 1892. Die Fortpflanzung der Wasserwellen. Zeitschrift des Vereines Deutscher Ingenieure 36: 947-954
  21. ↑ 21.0 21.1 Hughes, M.G. 1995. Friction factors for wave uprush. Journal of Coastal Research 13: 1089– 1098
  22. ↑ Puleo, J.A. and Holland, K.T. 2001. Estimating swash zone friction coefficients on a sandy beach. Coastal Engineering 43: 25– 40
  23. ↑ Puleo, J.A., Holland, K.T., Plant, N.G., Slinn, D.N. and Hanes, D.M. 2003. Fluid acceleration effects on suspended sediment transport in the swash zone. J.Geophys.Res. 108: C11 doi:10.1029/2003JC001943
  24. ↑ Raubenheimer, R., Elgar, S, and Guza, T. 2004. Observations of swash zone velocities: A note on friction coefficients. J.Geophys.Res. 109: C01027,1-8
  25. ↑ Puleo, J.A., Lanckriet, T. and Wang, P. 2012. Near bed cross-shore velocity profiles, bed shear stress and friction on the foreshore of a microtidal beach. Coastal Eng. 68: 6-16
  26. ↑ Inch, K., Masselink, G., Puleo, J.A., Russell, P. and Conley, D.C. 2015. Vertical structure of near-bed cross-shore flow velocities in the swash zone of a dissipative beach. Continental Shelf Res. 101: 98-108
  27. ↑ Hughes, M.G. and Baldock, T.E. 2004. Eulerian flow velocities in the swash zone: field data and model predictions. J. Geophys. Res. 109, C08009


The main author of this article is Job Dronkers
Please note that others may also have edited the contents of this article.
Citation: Job Dronkers (2026): Swash. Available from http://www.coastalwiki.org/wiki/Swash [accessed on 25-03-2026]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Swash&oldid=81869"