Shoreface profile

Definition of Shoreface: The shoreface is the nearshore zone of the inner continental shelf that is bounded landward by the mean low-water line and that extends seaward to where the influence of wave action on cross-shore sediment transport is on average minor compared to other influences. A similar definition is: The shoreface is the zone seaward of the shoreline where offshore generated waves interact with the upward sloping seabed. This is the common definition for Shoreface, other definitions can be discussed in the article

Definition of Shoreface profile: The shoreface profile, often called beach profile, is the cross-shore coastal depth profile of the shoreface. This is the common definition for Shoreface profile, other definitions can be discussed in the article

This article focuses on the shoreface of sandy coasts. The shoreface of rocky shores is described in the article Rocky shore morphology and the shoreface of mud coasts in the article Coastal mud belt.

Closure depth

Fig. 1. Schematic representation of a shoreface profile. The vertical/horizontal scale ratio is greatly exaggerated.

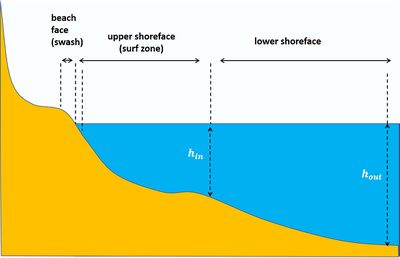
In the literature one can find various definitions of the shoreface. The definition given here, which is most commonly used, follows the definition given in Stive and De Vriend (1995). The shoreface can be divided in two zones, the upper shoreface and the lower shoreface. The upper shoreface is the zone where under average conditions waves break and the lower shoreface the zone where waves shoal. The lower part of the shoreface extends to the so-called outer closure depth [math]h_{out}[/math]; beyond this depth the seabed is hardly influenced by waves and wave-induced sediment transport is (on average) insignificant. The lower part of the shoreface is also called shoaling zone; wave shoaling is the process of wave amplification when waves travel from deep to shallow water before breaking (see Shallow-water wave theory). The outer closure depth [math]h_{out}[/math] has been empirically determined by Hallermeier (1981), yielding the formula (see also Closure depth)

[math]h_{out} \approx (H_s – 0.3 \sigma) \, T_s \sqrt{\large\frac{g}{5000 d_{50}}\normalsize} \approx 0.013 H_s T_s \sqrt{\large\frac{g}{d_{50}}\normalsize} , \qquad (1)[/math]

where [math]H_s, T_s[/math] are the average significant wave height and period, [math]\sigma[/math] is the wave height standard deviation, [math]d_{50}[/math] the medium sediment grainsize and [math]g[/math] the gravitational acceleration. The second approximation in Eq. (1) follows from the assumption of a Rayleigh wave distribution (see Statistical description of wave parameters). Typical values of the outer closure depth are in the range 15 – 40 m.

The definition of the outer closure depth implies that wave-driven sediment transport across this boundary is very small on average. It does not rule out significant sediment transport across this boundary due to e.g. tidal currents, wind-driven currents, ocean currents or internal waves. For example, the occurrence of shoreface-connected ridges (see Sand ridges in shelf seas) on the lower shoreface can be theoretically related to sediment transport by strong wind-driven currents. Other definitions of the outer boundary of the lower shoreface can also be found in the literature, for example the so-called Depth of Transport. This is the depth at which the total bed shear stress does not exceed the threshold of sediment transport under extreme storms. The Depth of Transport is typically further seaward than the outer closure depth Eq. (1).

Most energy is dissipated in the upper part of the shoreface, where wave overturning and breaking occurs. The depth where waves start breaking depends on the wave climate and is therefore highly variable. An often used definition of the transition depth [math]h_{in}[/math] between upper and lower shoreface was also given by Hallermeier (1978),

[math]h_{in} \approx 2.28 H_{12h/y}- 68.5 \Large\frac{ H_{12h/y}^2}{g T_{12h/y}^2}\normalsize , \qquad (2)[/math]

where [math]H_{12h/y}[/math] is the effective wave height just seaward of the breaker zone that is exceeded on average for 12 hours per year (i.e. the significant wave height with a probability of yearly exceedance of 0.137%) and [math]T_{12h/y}[/math] the associated wave period. Later refinements of this formula are discussed in the article Closure depth. Typical values of [math]h_{in}[/math] are in the range 3 – 10 m. The width of the upper shoreface typically ranges between about 100 - 1000 meters and the average slope between 1/10 and 1/100. The upper shoreface is sometimes also called breaker zone or surf zone, although onshore surfing wave bores usually only occur in the shoreward part of the upper shoreface. It is therefore preferable to use the designation upper shoreface as a fixed geographical indication, and the designations surf zone or breaker zone as a physical indication of the zone where broken waves surf onshore. This latter zone is narrow and close to the shoreline in a gentle wave climate and can be very wide under storm conditions, extending from the seaward boundary of the upper shoreface to the dune foot. Other subdivisions of the coastal profile include the active coastal zone, the beach face or foreshore and the backshore, see Definitions of coastal terms.

The division between upper and lower shoreface profiles is often marked by an inflexion point, a bar or a terrace, indicating transition of morphodynamics (Fig. 1). Another indicator of the transition between upper and lower shoreface is a break in the trend of the sediment grainsize with depth. The shoreface is bordered on the landward side by the beach face. This is the zone where under average conditions waves collapse and run up the beach (see Swash zone dynamics). The upper shoreface profile is often undulated due to the presence of one or several bars, see Nearshore sandbars. These bars have mainly a shore parallel orientation, but more complex three-dimensional patterns are ubiquitous (see Rhythmic shoreline features and Fig. 3).

Morphodynamic feedback

Sediment transport on the shoreface depends on the local wave climate. By 'wave climate' is meant the description of incoming waves in terms of a statistical distribution of incident wave directions, wave heights and wave periods (see Statistical description of wave parameters). Sediment transport also depends on the characteristics of bed sediments and on the seabed bathymetry. For small wave incidence angles (close to the shore-normal direction) the relevant seabed bathymetry is the cross-shore shoreface profile.

Fig. 2. Gold Coast, Australia, before and after the June 1967 cyclone. Observed shoreface profiles showing recovery of the initial close-to-equilibrium profile after strong perturbation by an extreme event. Redrawn after Patterson and Nielsen (2016).

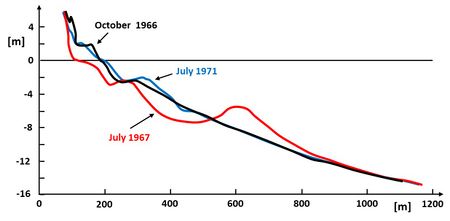
The shoreface profile influences cross-shore sediment transport, but the inverse is also true: changes of the shoreface profile result from gradients in the cross-shore sediment transport. This is called morphodynamic feedback: for a given incident wave field the shoreface profile determines the transformation of the wave field on the shoreface and therefore the resulting sediment transport, whilst the resulting sediment transport determines the shoreface profile. As a result of this morphodynamic feedback, the shoreface profile tends to an equilibrium shape for a given stable wave climate. An illustration is presented in Fig. 2, which shows the recovery after strong perturbation of a shoreface profile that is initially close to equilibrium.

A dynamic equilibrium is reached when onshore directed sediment transport and offshore directed transport are equal on average over a period exceeding the morphodynamic adaptation time. This holds for alongshore uniform coasts; the equilibrium requirement for non-uniform coasts is a vanishing divergence of the long-term average total sediment transport vector (cross-shore and alongshore). It was realised already long ago that the shoreface of a sedimentary coast should not be regarded as a geologically inherited feature, but as the result of natural adaptation to modern hydrodynamic conditions and sediment supply. In real field situations, a coast never assumes its equilibrium profile; it is always in a transient state due to fluctuations in the wave climate and the mean water level. The coastal profile deviates from the equilibrium profile, even in the hypothetical case of a stationary wave climate, due to the cyclical or quasi-cyclical migration of seabed structures along the profile (see Nearshore sandbars).

Knowing how to determine the equilibrium shoreface profile has great practical interest. It provides quantitative insight in the response of the shoreface to changes in the local wave climate by human and natural causes; such insight is important for testing and improving the effectiveness of measures to combat coastal erosion and shoreline retreat.

Bedforms and sediment sorting

Morphodynamic feedback involves not only shoreface profile development, but also sediment grainsize and bed roughness. Grainsize and bed roughness strongly influence sediment transport . Inversely, sediment transport strongly influences the grainsize distribution of bed sediments. Bed roughness depends on the presence of bedforms (ripples, dunes), which in turn depend on sediment transport and sediment grainsize. Consequently, shoreface profile development, wave transformation on the shoreface, sediment transport, grainsize sorting and bedform emergence are all dynamically coupled processes.

Grainsize sorting is primarily due to differences in transport modes of different grainsize fractions. The finer fractions are more easily brought and maintained in suspension than the coarser fractions. They are transported further away from their initial location and tend to settle on the lower shoreface zone where wave-induced bed shear stresses are lower than on the upper shoreface. The coarse fraction is transported partly as suspended load and partly as bedload in the wave boundary layer. Wave transformation in shallow water leading to wave skewness (stronger onshore than offshore wave orbital velocity) and wave asymmetry (stronger onshore than offshore wave orbital acceleration) favour net onshore transport in the wave boundary layer. Fine sediments are resuspended from the upper shoreface due to undertow currents, longshore currents and turbulent shear stresses generated by breaking waves. Sediments on the upper shoreface are therefore coarser than on the lower shoreface. Fine sediment particles can still be present on the upper shoreface if they are 'hidden' by overlying coarser sediment particles – a phenomenon called 'bed armoring' (see Seabed armoring).

Fig. 3. The barred coast of North Holland, The Netherlands. https://beeldbank.rws.nl, Rijkswaterstaat / Rens Jacobs

The largest bedforms on the shoreface, such as shoreface-connected ridges (scale of several kilometers) and shore-oblique bars (scale of the order of hundred meters) are mainly related to morfodynamic feedback processes that interact with longshore transport, see the articles Sand ridges in shelf seas and Rhythmic shoreline features. Other large bedforms, the so-called nearshore sandbars or breaker bars (scale also of the order of 100 meters, Fig. 3) arise from morphodynamic coupling with the wave breaking process, through the resulting flow structure at the breaker bar and interaction with cross-shore and longshore currents - see Nearshore sandbars for a more detailed discussion. Bedforms at much smaller scales – ripples with wavelengths of the order of 0.3 - 1 m – are formed in the less exposed parts of the shoreface under low to moderate wave conditions. They are often found on the lower shoreface and in the troughs between nearshore breaker bars. Morphodynamic feedback processes, leading to regular ripple patterns, involve ripple-induced near-bed flow circulation, vortex shedding at ripple crests and non-linear ripple-ripple interactions. For a more detailed discussion, see the articles Wave ripples and Wave ripple formation. The time lag of sediment suspension and settling related to vortex shedding at the ripple crests strongly influences the direction of residual cross-shore sediment transport on the shoreface, see section #Onshore wave-induced sediment transport.

Beach classification; dissipative and reflective

The beach profile in the upper shoreface zone can be highly variable. The profile tends to steepen in periods of low-energy waves (especially long-period swell waves) and to flatten under high-energy storm waves (see Active coastal zone). Sediment characteristics, which largely depend on the supply source (see Coastal and marine sediments), also play an important role. Coarse-grained beaches typically have steeper slopes than fine-grained beaches. Gently sloping beaches dissipate almost completely the energy of incident waves, whereas steep-sloping beaches tend to reflect (partly) incident waves. For distinguishing between reflective and dissipative beaches the Dean-parameter [math]\Omega[/math] is often used :

[math]\Omega = \Large \frac{H_b}{wT_p} \normalsize , \qquad(3)[/math]

where [math]H_b[/math] is the significant wave height at breaking, [math]T_p[/math] is the peak spectral wave period and [math]w[/math] is the mean sediment fall velocity.

Fig. 4. Beach morphologies according to the parameters [math]\Omega[/math] and [math]RTR[/math], based on beach surveys in England, Wales, Northern Ireland, Australia and China. Reflective beaches are found in the red zone and dissipative beaches in the blue zone.

Wright and Short (1984) analysed beach profiles in Australia by evaluating the parameter [math]\Omega[/math], considering the local long-term average wave climate. They found that beach types could be classified as follows :

• reflective beaches correspond to [math]\Omega \lt 1 [/math];
• intermediate beaches correspond to [math]1\lt \Omega \lt 6 [/math];
• dissipative beaches correspond to [math]\Omega \gt 6 [/math].

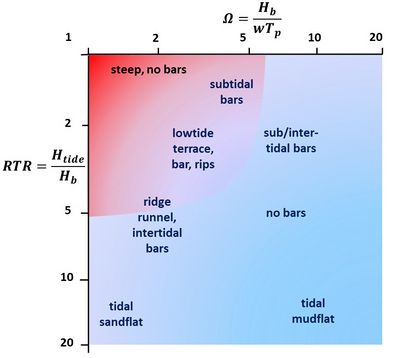
The tidal range [math]H_{tide}[/math] also influences the beach profile, because the surf zone is shifted across the shoreface with tidal level. For large tides (tidal range much larger than wave height) the surf zone covers during the tidal cycle a much larger area than for small tides. Beaches with large tides therefore have smaller upper shoreface slopes compared to beaches with the same [math]\Omega[/math] and small tides.

Several field studies have been performed to relate beach profiles to different combinations of the Dean parameter [math]\Omega[/math] and the relative tidal range [math]RTR=H_{tide}/H_b[/math]. Distinction is made between different beach morphologies: reflective beaches with steep graveled slopes, reflective/intermediate beaches with subtidal bars, intermediate beaches with rip cells and low-tide terrace or low-tide bar, dissipative beaches without significant bar formations, dissipative beaches with multiple inter-tidal bars and dissipative beaches with tidal flats, see Fig. 4. The figure only gives a rough indication of beach morphologies, because the natural variability is not fully captured by the two dimensionless parameters [math]\Omega[/math] and [math]RTR[/math]. Other factors play a role, in particular the temporal variability in morphology and environmental conditions and the role of geology.

Another parameter that is often used for analysing the beach response to variations in the wave climate is the so-called surf similarity parameter that relates the wave steepness (wave height to wave length ratio) to the surf zone slope.

Difference between upper and lower shoreface

The upper shoreface is the zone where the energy of incident waves is converted into water level gradients, currents, seabed agitation and sediment transport. This goes with strong morphodynamic activity manifested in profile change, generation of bedforms and shoreline advance or retreat. In contrast, wave energy dissipation on the lower shoreface is small and hardly affects the wave energy flux toward the coast, [math]F^{(x)} = c_g H_s^2 \cos \alpha[/math], which can therefore be considered constant (Green's law; see Table Symbols for the symbols). Assuming approximate validity of linear wave theory, [math]c_g \approx c \approx \sqrt{gh}[/math], the height of waves propagating to shallower waters increases as [math]H_s \propto h^{-1/4}[/math]. While shoaling, these waves develop wave skewness and asymmetry on the lower shoreface (see Appendix). Wave skewness and asymmetry generate net sediment transport (see next paragraph) and therefore play an important role in shaping the cross-shore profile.

Sediment transport rates on the lower shoreface are much smaller than on the upper shoreface, implying a long adaptation time scale to changes in sea level and wave climate. On the upper shoreface these time scales are on the order of day-year, compared to decade-millennium time scales on the lower shoreface. Besides, waves are not the only sediment transport agent on the lower shoreface; tidal currents and wind-driven currents are important as well. The strongest currents are associated with extreme events (storm surges, cyclones), but persistent wind stress over longer periods can produce up or downwelling and associated up or downslope sediment transport. At places where river plumes flowing along the coast induce a cross-shore salinity gradient, fine sediment can be trapped on the lower shoreface and even on the upper shoreface, as explained in the article Coastal mud belt. However, on exposed coasts, energetic waves will transport fine sediment from the upper to the lower shoreface. The lower shoreface can also receive sediment directly from nearby river deltas. When sediment sources are absent or sparse, the seabed sediment of the lower shoreface has mainly a relict origin with possibly rocky outcrops, indurated clay or coarse terrigenous deposits. Biotic activity on the lower shoreface can be intense with a high production of calcareous bioclasts. The lower shoreface can therefore act as a source of calcareous sand to the upper shoreface and the beach.

Cross-shore sediment transport

Direct observation of net cross-shore sediment transport and its separate components in the field is difficult. This is particularly true for the surf zone, where the temporal and spatial variability of transport processes is very high. The hydrodynamic conditions for the installation and operation of measuring devices are harsh, especially in periods where sediment transport is most significant. Bottom-mounted pressure sensors are most often employed for the determination of wave characteristics. This can easily yield erroneous (underestimated) values if the nonlinearity of wave dynamics is not accounted for. Acoustic and optical sensors are sensitive to air bubbles. Their use for determining suspended sediment concentrations and grainsizes is hampered as breaking waves entrain large volumes of air. For these reasons, most knowledge is derived from laboratory experiments. Knowledge from the field is often obtained indirectly, through interpretation of the observed erosion and accretion patterns produced by cross-shore sediment transport. Mathematical models are often used as interpretation tools.

Sediment transport on the shoreface depends on many processes. The focus is on processes relevant to cross-shore transport. It should be realised, however, that longshore transport processes can also play an important role, for example by influencing the sediment balance of the shoreface or by generating various kinds of bedforms, see for example the articles: Natural causes of coastal erosion, Littoral drift and shoreline modelling and Rhythmic shoreline features. In the following we consider sandy beaches, with grain sizes typically between 0.2 and 0.5 mm (fine to medium sand). Coarse sedimentary beaches are dealt with in the article Gravel Beaches.

Fig. 5. Sand transport over a steep vortex bed ripple in the Aberdeen oscillatory flow tunnel. The horizontal orbital motion is skewed: the velocity to the right (wave propagation direction) is stronger than to the left, but the duration is shorter. The high orbital velocity to the right creates a sand-laden vortex on the lee-side of the ripple crest, which is swept back over the ripple right after flow reversal. Courtesy: Jebbe van der Werf.

A distinction is often made between bedload transport and suspended load transport. Bedload transport represents the motion of sediment particles that are dragged by the flow along the seabed, either by rolling or successive jumps (saltation) or by entrainment of a thin seabed top layer (so-called sheet flow layer, of typically 10-30 grains thick). Suspended load represents the transport of sediment particles that have been brought into suspension by turbulent fluid motions. An important difference between the two transport modes is the phase between the load of the transported sediment and the instantaneous flow velocity, especially in the case of wave-induced flow. Bedload responds almost instantaneously to changes in the wave orbital velocity; increase (decrease) of velocity implies immediate increase (decrease) of bedload. This implies that an onshore (offshore ) flow asymmetry (so-called velocity skewness) with higher peak velocity in onshore (offshore) flow induces a net bedload transport in onshore (offshore) direction. Suspended load generally displays a fast response to an increase in flow velocity; sediment particles can be lifted quickly from the seabed and brought into suspension when the flow velocity increases (Fig. 5). However, unlike bedload, the response of the suspended sediment concentration to a decrease in flow velocity depends on the settling velocity of sediment particles, which induces a response delay that can be substantial compared to the wave period. Asymmetries in onshore (offshore) wave orbital flow are therefore less decisive for the net direction of suspended load than for bedload. In the surf zone where the waves break, suspended load transport dominates. Flume experiments suggest that bedload transport dominates in situations where unbroken waves approach the shore, e.g. on the lower shoreface and on steep, reflective beaches.

As explained below, onshore transport on the shoreface is mainly related to bedload transport and offshore transport to suspended load transport. As bedload transport involves mainly the coarse sediment fraction whilst suspended load transport involves mainly the fine sediment fraction, it follows that under average conditions coarser sediment is preferentially transported onshore and finer sediment offshore.

Wave-induced onshore sediment transport

Wave transformation in shallow water is a major factor for onshore sediment transport . Due to shoaling effects, starting on the lower shoreface, onshore propagating waves become increasingly skewed (velocity skewness: onshore peak orbital flow stronger than offshore peak orbital flow) and forward leaning asymmetric (acceleration skewness: offshore-to-onshore flow reversal faster than onshore-to-offshore flow reversal), see the Appendix for details. These asymmetries in the wave orbital velocity produce shear stresses on the seabed which are stronger in onshore direction than in offshore direction , see also Shallow-water wave theory. Wave skewness is primarily effective for inducing onshore bedload transport rather than suspended load transport, since bedload transport responds almost instantaneously to changes in near-bed velocities. Wave skewness and asymmetry are most pronounced on gently sloping dissipative coasts; they hardly develop on steep reflective coastal profiles.

Fig. 6. Model simulations of the horizontal wave orbital velocity [math]U[/math] and sediment transport [math]Q[/math] averaged over the ripple length for acceleration-skewed waves, velocity-skewed waves and acceleration+velocity-skewed waves. The net transport is directed offshore for the velocity-skewed wave and onshore for the acceleration-skewed and velocity+acceleration skewed waves. Adapted from Salimi-Tarazouj et al. (2024).

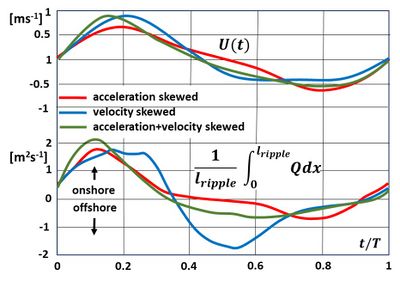
Phase lags between bed shear stress and suspended sediment concentration determine to which degree wave skewness induces onshore transport. In some situations (rippled bed, fine sands) a large phase lag can reverse the net direction of suspended sediment transport. A large time lag implies that sediment particles that are stirred up by turbulent eddies during onshore orbital motion are transported offshore after reversal of the wave orbital velocity, see figures 5 and 6. Although strongly skewed waves promote onshore ripple migration, the net sediment transport can be directed offshore by the asymmetric contribution of ripple vortex entrainment. Van der Werf et al. (2006) showed that the suspended sand transport magnitude scales with the vortex suspension parameter [math]P=[/math] ripple height/median grainsize diameter, and that for values of [math]P[/math] above a critical range of 70–90, the total net transport rate is offshore directed due to the larger magnitude of the ripple vortex induced suspended transport compared to the onshore directed bedload transport (driving the onshore ripple migration).

The picture changes in the presence of acceleration skewness (also called wave asymmetry), which stimulates onshore transport. The strong acceleration of the orbital flow at the offshore-to-onshore flow reversal creates a sediment-laden vortex on the stoss side of bed ripples, which travels toward the onshore direction as it is carried by the onshore ambient flow, see Fig. 6. The ripple-averaged net sediment transport rate is in the direction of highest-acceleration (onshore) and increases with acceleration skewness. The role of acceleration skewness can be explained in several ways. One explanation refers to asymmetry in the thickness of the boundary layer. The onshore-directed bed shear stress is particularly strong just after the rapid reversal of the flow from offshore to onshore orbital motion, because the boundary layer is still very thin at that time (see Figure A1). Another explanation refers to the pore pressure gradient in the upper layer. Under steep forward-leaning waves, the maximum pore pressure gradient has an onshore-directed component that is conducive to net onshore sheet flow. Flume experiments showed that maximum horizontal pore pressure gradients were strongly correlated with local wave steepness, whereas pressure gradients were larger for larger acceleration skewness within each wave period.

Wave breaking that generates turbulent fluid motions and sediment resuspension under the wave crest also contributes to onshore transport, especially in the case of plunging waves. But at the same time, wave breaking removes most of the wave skewness, thus reducing the associated onshore sediment transport component in the surf zone.

Longuet-Higgins (1953) has shown theoretically that progressive waves generate a net forward streaming at the top of the wave boundary layer. This forward streaming can provide a further contribution to onshore transport. The theory only holds for smooth beds and not in cases where the seabed is rippled, in cases of strongly skewed waves, or for sheet flow conditions (see also Sediment transport formulas for the coastal environment). Due to the high sediment concentration in the streaming layer (and in spite of the small vertical extent of the layer and the low flow velocity), the contribution of wave driven near-bed streaming to onshore transport is significant, especially in the shoaling zone and surf zone prior the plunging point.

Wave-induced offshore sediment transport

Offshore transport is mainly due to so-called undertow: the compensating return current for the net onshore mass transport in the upper water column between wave trough and wave crest . The offshore suspended sediment transport by the undertow current is particularly strong just landward of the location where waves are breaking (plunging waves) and where much sediment is brought into suspension by wave energy dissipation and by the longshore current. Although the undertow velocity is smaller than the amplitude of the wave orbital velocity, it produces substantial offshore transport across the shoreface, in particular in the surf zone, where it often dominates the onshore transport related to wave-asymmetry effects. The undertow current is strongest near the bottom in the surf zone, whereas it peaks near the surface on the lower shoreface. On the lower shoreface it is largely offset by onshore-directed Stokes drift and therefore less effective for offshore transport. However, extreme storms can transport sand from the upper shoreface so far down the lower shoreface and towards the inner shelf, that onshore transport processes under more moderate wave conditions are not strong enough to bring the sand back.

Bound infragravity waves may also contribute to net offshore sediment transport, as discussed in the article Infragravity waves. The transport component related to infragravity waves can be quite substantial on dissipative beaches, but the net contribution is subdued after wave breaking because the phase relationship with incident waves is lost and the net sand transport can be either onshore or offshore directed. However, small transport contributions cannot be ignored because the large transport components related to wave skewness / asymmetry and undertow largely cancel each other out. For this reason, the downslope transport component must also be considered, see next section.

Downslope sediment transport

Several mechanisms can induce downslope sand transport. We do not consider here downslope turbidity currents or mud avalanching that may occur at the outer edge of deltas loaded with large amounts of fluvial sediment.

One mode of downslope transport consists of sand particles rolling down the shoreface slope. However, modeling suggests that this does not contribute significantly to downslope transport for fine to medium sandy beaches.

A second transport mode is so-called wave-supported gravity flow (WSGF). Observations on the Dutch coast show that wave stirring of the seabed under storm conditions can generate and sustain a high-density layer of suspended fine sand (thickness 15-20 cm, concentration exceeding 40 g/l) flowing down the shoreface slope (1/100 - 1/200) with a velocity of a few cm/s . Modeling suggests that the high-density sediment layer is kept in suspension by the combined action of wave-induced turbulent stresses and hindered settling. The wave-supported gravity flow was observed during a storm with near-bed wave orbital velocities of about 0.5 m/s, lasted for more than a day and far exceeded in volume other cross-shore sand transport processes. However, the frequency of occurrence of WSGF events is not well known. Wave-supported gravity flows have also been observed on the shoreface of muddy coasts.

A third mechanism of downslope transport is related to the wave orbital excursion that moves sediment particles between zones of nearshore high bed shear stress and offshore low bed shear stress. Since resuspension after settling takes more time lower on the shoreface than higher on the shoreface, the downslope distance traveled by settling sediment particles is on average longer than the onshore distance. The average difference between offshore and onshore travel distance depends not only on the orbital excursion and shoreface slope, but also on the particle settling velocity. During the offshore excursion, sediment particles with a lower settling velocity settle later, thus lower, on the shoreface where the bed shear stresses are lower and the resuspension time longer. Fine sediment particles thus experience greater downslope transport than coarse particles. The slope effect requires a correction to the net sediment transport over a flat bottom, which is an increasing function of the product of bed slope [math]\tan \beta[/math] and wave orbital excursion, and a decreasing function of the fall velocity [math]w[/math]. Empirical formulas for suspended sediment transport assume in general that the slope effect can be represented by a correction factor to the instantaneous wave-induced transport components of the form

[math](1- \gamma_s \Large \frac{u}{w} \normalsize ) \, \tan \beta, \qquad (4)[/math]

where [math]u[/math] is the instantaneous wave orbital velocity, [math]w[/math] the sediment fall velocity and [math]\gamma_s[/math] an adjustable parameter depending, among other things, on the resuspension processes. This is consistent with laboratory experiments, in which an approximate correspondence was found between coastal profiles and an adjusted Dean parameter

[math]\Omega_{\beta} = \Large \frac{H_s \tan \beta}{wT_p} \normalsize . \qquad(5)[/math]

Experiments by Hattori and Kawamata (1980) with different profile slopes show that onshore transport dominates for [math]\Omega_{\beta} \lt 0.08[/math] and offshore transport dominates for [math]\Omega_{\beta} \gt 0.08[/math]. An equilibrium slope corresponds to (order of magnitude)

[math]\Omega_{\beta} \sim 0.08. \qquad(6)[/math]

Comparison with Eq. (3) shows that reflective beaches have a steep slope and dissipative beaches a gentle slope. The presence of the fall velocity [math]w[/math] in the denominator of the downslope correction term in Eq. (4) also implies that net wave-induced transport can be downslope (offshore) for fine sediment even if upslope transport (onshore) prevails for coarse sediment.

Although not proven, it is often assumed that the slope effect is a major factor compensating for net wave-induced onshore transport (sum of all wave-induced onshore and offshore transport components including undertow) in situations close to equilibrium. This implies that the equilibrium shoreface slope [math]\tan \beta [/math] will be steeper (larger [math]\tan \beta [/math]) for a coarser seabed (large fall velocity [math]w[/math]) than for a finer sediment bed (small fall velocity [math]w[/math], smaller [math]\tan \beta [/math]). This is expressed by the correction factor (Eq. 4) and is in general agreement with field observations. An analysis of long-term shoreface profile observations at the Gold Coast (Australia) suggests that the bed-slope effect on the total net sediment transport averaged over the wave period (or, more generally, the wave climate) can be related to the equilibrium bed slope [math]\tan \beta_{eq}[/math] by the correction factor [math](1 – \tan \beta / \tan \beta_{eq})[/math] , which is equivalent to Eq. (4).

Shoreface modelling

The processes involved in sediment transport on the shoreface, as described above, are complicated and not yet fully understood. Even the most sophisticated numerical morphodynamic models, like Delft3D and XBEACH , make use of approximate empirical formulations for several processes contributing to sediment transport and involve parameters that need to be tuned. Empirical formulas for wave-induced sediment transport on the shoreface that are often used in practice are given in the articles Sediment transport formulas for the coastal environment and Sand transport. These formulas are based on laboratory and field measurements for a large range of conditions. Rough estimates can be obtained with the empirical default parameters given in these articles. For more accurate site-specific estimates it is necessary to tune these parameters to field data. A more detailed discussion of shoreface modelling is presented in the article Modelling coastal hydrodynamics.

Equilibrium shoreface profile (sandy beach)

Fig. 7. The Bruun/Dean profile (Eq. 7) and the equivalent Bodge profile (Eq. 8).

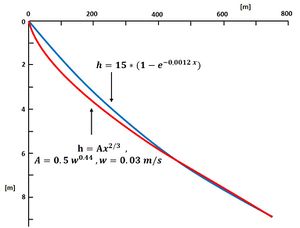
For a given stable wave climate the shoreface profile tends after a certain (long) period to an equilibrium profile, as pointed out before. This equilibrium profile can be computed by applying sediment transport formulas to an initial profile for a period comprising all wave conditions according to local wave climate statistics. This requires heavy calculations that are moreover subject to large uncertainty margins. Therefore, equilibrium profiles derived from field observations are often used. By analyzing a large number of beach profiles of the Californian and Danish coasts and the US Atlantic and Gulf coasts Bruun (1954) and Dean (1977) derived an equilibrium profile (often called the Dean/Bruun profile) of the form (Fig. 7)

[math]h(x)=A \; x^{2/3}, \qquad(7)[/math]

where [math]h[/math] is the water depth [m], [math]x[/math] the cross-shore distance [m] ([math]x=0[/math] at the shoreline) and [math]A[/math] a coefficient depending on the sediment fall velocity [math]w[/math] [m/s]. Dean (1987) empirically determined [math]A \approx 0.5 \; w^{0.44} [/math] [m^1/3]. Another estimate was given by Kriebel et al. (1991) [math]A \approx 2.25 \; (w^2/g)^{1/3}[/math] [m^1/3]. In Eq. (7) it is implicitly assumed that the fall velocity is uniform across the shoreface profile.

Dean showed that the exponent 2/3 is consistent with the assumption of constant wave energy dissipation per unit volume throughout the surf zone.

Because the Bruun/Dean profile has an infinite slope at the shoreline, an alternative form was proposed by Bodge (1992) ,

[math]h(x)=B \; (1 – e^{-kx}) , \qquad(8)[/math]

where [math]k[/math] is an empirical coefficient in the range [math]500 \lt k^{-1} \lt 2000 [/math] [m] and where the coefficient [math]B[/math] is related to the beach slope [math]\tan \beta=Bk[/math] at the shoreline [math]x=0[/math].

Fig. 8. Theoretical equilibrium profile for the upper shoreface (Eq. 7) and lower shoreface (Eq. 9).

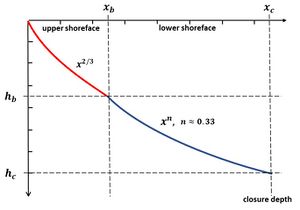
The Bruun/Dean profile provides in general a reasonable description of observed long-term averaged profiles of micro-mesotidal sandy coasts. This holds in particular for the upper shoreface where breaking waves are the dominant driving agent for sediment transport. The 2/3 power law is generally less adequate for describing the profile of the lower shoreface. This is not surprising, as sediment transport here is mainly driven by non-breaking waves. In a simplified ideal situation, based on realistic assumptions, a theoretical profile was derived through application of the principle of minimum energy dissipation. The theoretical profile also follows a power law (see Fig. 8):

[math]h(x) = \Big[ h_b^{1/n} + (h_c^{1/n} - h_b^{1/n}) \Large\frac{x - x_b}{x_c - x_b}\normalsize \Big]^n , \quad x_b \lt x \lt x_c , \qquad (9)[/math]

where [math]h_b=h(x_b)[/math] is the depth at the transition from upper to lower shoreface and [math]x_b[/math] the corresponding location, and [math]h_c=h(x_c)[/math] is the closure depth and [math]x_c[/math] the corresponding location. The exponent [math]n[/math] has a value in the range 0.3 - 0.4, depending on the formulation of the bottom friction. Inman et al. (1993) found best fits with exponents ranging between 0.3 and 0.45 from an analysis of beach profiles for the coasts of south California, North Carolina and the Nile delta.

For gravel beaches other cross-shore profiles are found, see Gravel Beaches.

Analytical equilibrium models

Because of the earlier mentioned difficulties to derive model estimates of the equilibrium shoreface profile, taking wave climate statistics fully into account, analytical models have been developed in which the wave climate is replaced by a single representative monochromatic incident wave. In these models an alongshore uniform shoreface is assumed with perpendicular wave incidence, and a simple wave transformation model is used based on depth saturation of broken waves (wave height limited by depth) and shallow-water wave theory. An analytical expression for the equilibrium shoreface slope can be derived by requiring that the total wave-integrated cross-shore sediment flux equals zero throughout the shoreface zone . Although these models reproduce certain properties also observed in the field, such as increasing profile steepness with increasing grain size and with increasing wave period, a more detailed comparison of computed profiles with observations exhibits large discrepancies. This is perhaps not surprising in view of the simplicity of the model used for wave-induced sediment transport, which assumes zero phase difference between wave-orbital velocity and sediment load, and which ignores many other processes described in the previous paragraphs. It has been shown that some discrepancies can be repaired by using expressions for the sediment transport components derived from field observations.

Analytical models also ignore the influence of extreme storms, which can flatten the profile out to great depths within a short period. The profile adaptation time scale for the entire shoreface being quite long, it is plausible that observed shoreface profiles generally correspond to transient profiles .

Related articles

Nearshore sandbars

Bruun rule

Active coastal zone

Shoreline retreat and recovery

Coastal Hydrodynamics And Transport Processes

Modelling coastal hydrodynamics

Coastal and marine sediments

Gravel Beaches

Further reading

Komar, P.D. 1998. Beach processes and sedimentation. Prentice Hall, London, pp. 544.

Woodroffe, C.D. 2002. Coasts, form, processes and evolution. Cambridge Univ.Press, 623 pp.

Dronkers, J. 2017. Dynamics of Coastal Systems. World Scientific Publ. Co. 753 pp.

Table Symbols

Variable	Description	Variable	Description
[math]c[/math]	wave propagation speed ([math][m/s][/math])	[math]c_g[/math]	wave group propagation speed ([math][m/s][/math])
[math]d_{50}[/math]	mean sediment grainsize ([math][m][/math])	[math]g[/math]	gravitational acceleration ([math]\approx 9.8 \; m/s^2[/math] )
[math]h[/math]	water depth ([math][m][/math])	[math]h_b[/math]	water depth at breaking location ([math][m][/math])
[math]H_b[/math]	significant wave height at breaking location ([math][m][/math])	[math]H_s[/math]	significant wave height ([math][m][/math])
[math]k[/math]	wave number ([math][m^{-1}][/math])	[math]t[/math]	time ([math][s][/math])
[math]T_p[/math]	spectral peak wave period ([math][s][/math])	[math]u[/math]	velocity ([math][m/s][/math])
[math]w[/math]	sediment fall velocity ([math][m/s][/math])	[math]x[/math]	distance from shoreline (seaward >0, [math][m][/math])
[math]\alpha[/math]	wave incidence angle	[math]\tan \beta[/math]	shoreface slope
[math]\theta[/math]	wave phase [math]\theta = \omega t - kx[/math]	[math]\rho[/math]	seawater density ([math][kg/m^3][/math])
[math]\omega[/math]	radial wave frequency ([math][s^{-1}][/math])	[math]\Omega[/math]	Dean parameter ([math]= \Large \frac{H_b}{wT_p} \normalsize [/math])

Appendix: Wave skewness

When a sinusoidal wave travels into shallow water the wave shape changes. The equations describing wave motion in deep water are almost linear; the solution is a simple sinus-shaped wave. The nonlinear terms in the wave equations become important in shallow water. These nonlinear terms introduce higher harmonic wave components in the solution. Initially, the first harmonic components grow the fastest. The wave orbital velocity can then be written as

[math]u(\theta) = U_1 \cos(\theta) + U_2 \cos(2\theta) + V_2 \sin(2\theta) , \qquad (A1)[/math]

where [math]\theta = \omega t - kx[/math] is the wave phase, with [math]t=[/math]time, [math]x=[/math]the distance travelled in the wave propagation direction, [math]\omega =[/math]the wave angular frequency, [math]k=\omega / c=[/math]the wave number and [math]c=[/math]the wave propagation speed. The [math]U_2[/math] component represents the velocity skewness [math]S_u[/math] and the component [math]V_2[/math] represents the wave asymmetry or acceleration skewness [math]A_u[/math] (Fig. A1).

Fig. A1. Wave orbital velocity as function of the phase [math]\theta[/math]. Left panel: Velocity skewness. Right panel: Acceleration skewness. Blue curves: Eq. (A1). Red curves: Eq. (A5). Positive acceleration skewness stimulates onshore bedload transport, because the fast increase of the onshore orbital motion leaves the boundary layer barely time to grow, leading to strong near-bed velocity gradients and shear stresses. It has been suggested that high pressure forces under the steep wave front also play a role by mobilizing bed grains around flow reversal.

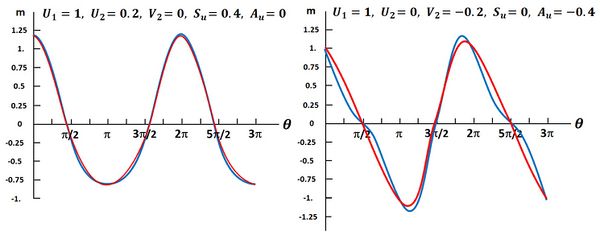
We define [math] \lt …\gt \equiv \Large\frac{1}{2 \pi}\normalsize \int_0^{2 \pi} … d \theta [/math] and assume [math]|U_2|,|V_2| \lt \lt |U_1| .[/math]

The velocity and acceleration skewness are defined as

[math]S_u \equiv \Large\frac{\lt u^3\gt }{\lt u^2\gt ^{3/2}}\normalsize \approx \Large\frac{3 U_2}{\sqrt{2} U_1}\normalsize, \quad A_u \equiv \Large\frac{ \lt (\mathcal{H}u)^3 \gt }{\lt (\mathcal{H}u)^2\gt ^{3/2} }\normalsize \approx \Large\frac{3 V_2}{\sqrt(2) U_1}\normalsize . \qquad (A2)[/math]

(the Hilbert transform [math]\mathcal{H}[/math] applied to sinusoidal functions gives: [math]\mathcal{H}cos(x)=-sin(x), \; \mathcal{H}sin(x)=cos(x), \; \mathcal{H}cos(2x)=-sin(2x), \; \mathcal{H}sin(2x)=cos(2x)[/math], etc).

By analysing a large number of field observations of the wave orbital velocity on the shoreface, Ruessink et al. (2012) found empirical evidence that the velocity and acceleration skewness mainly depend on the Ursell number

[math]U_r = \Large\frac{3 g H}{8 h^2 \omega^2}\normalsize , \qquad (A3)[/math]

where [math]g \approx [/math]9.8 m s^-2 is the gravitational acceleration, [math]H[/math] the significant wave height and [math]h[/math] the local depth. They established the empirical expressions

[math] (S_u^2+A_u^2)^{-1/2} = 1.17 \, (1 + 0.205 \, U_r^{-3.37}), \quad \Large\frac{A_u}{S_u}\normalsize = -\cot \Big(\Large\frac{\pi}{2}\normalsize \tanh \big(0.815 U_r^{-0.672}\big)\Big) \normalsize, \qquad (A4)[/math]

from which [math]S_u[/math] and [math]A_u[/math] can be solved. Besides the Ursell number, also other factors influencing the velocity and acceleration skewness have been identified, such as the offshore wave steepness, spectral band width and beach slope.

Abreu et al. (2010) derived a more general expression than Eq. (A1) for the wave orbital velocity, that includes velocity skewness and acceleration skewness,

[math]u(\theta)=U_1 \Large\frac{\sqrt{1-r^2}}{1+\sqrt{1-r^2}} \, \frac{r \sin{\phi}+(1+\sqrt{1-r^2}) \sin(\theta)}{1 - r \cos(\theta +\phi)}\normalsize . \qquad (A5)[/math]

The parameters [math]r[/math] and [math]\phi[/math] are related to the velocity skewness and acceleration skewness by

[math]r = \Large\frac{2 \sqrt{p+1}}{p+2}\normalsize, \quad p = \Large\frac{9}{2 (S_u^2+A_u^2)}\normalsize , \quad \phi = -\Large\frac{\pi}{2}\normalsize -\arctan(A_u/S_u) . \qquad (A6)[/math]

A predictive model for wave-induced cross-shore sediment transport can be obtained by using the expression (A5) for the wave orbital velocity in formulas for cross-shore sediment transport, for example the formulas presented in the article Sediment transport formulas for the coastal environment. This yields only the transport contribution of the oscillatory wave component. Other components of cross-shore sediment transport discussed above have to be considered as well.

References

The main author of this article is Job Dronkers Please note that others may also have edited the contents of this article. Citation: Job Dronkers (2024): Shoreface profile. Available from http://www.coastalwiki.org/wiki/Shoreface_profile [accessed on 22-12-2024] For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Dronkers J