Shoreline retreat and recovery
Two types of processes can be responsible for shoreline retreat and advance. One type is beach erosion/accretion related to structural sand loss/gain on the active coastal zone. The other type is beach erosion/accretion related to temporal variations of the shoreline. The first type refers to adaptation of the beach state to long-term trends and changes in external conditions. Examples are: relative sea-level rise (see: Bruun rule), long-term trends in wave climate, decrease/increase of sand supply by rivers, trapping of sand in inlets and submarine canyons and human interventions that alter longshore sand transport[1]. See, for example, Human causes of coastal erosion, Natural causes of coastal erosion and Erosion hotspots for further details.
The second type of beach erosion/accretion is a shift of the shoreline with a reversible character (no consistent long-term trend), in most cases related to natural variability of hydrodynamic conditions in the coastal zone. This shoreline shift can be a seasonal fluctuation, but it can also be a multiannual phenomenon induced by exceptional hydrometeorological conditions. In the following paragraphs, we take a closer look at this type of shoreline variability. It should be emphasized that coastal retreat and partial recovery are often the combined result of structural coastal erosion/accretion and temporary shoreline fluctuations.
Contents
Shoreline fluctuations are not synonymous with coastal erosion and accretion
The terms shoreline retreat (advance) and coastal erosion (accretion) are sometimes used without distinction. The shoreline position is generally defined as the high water (HW) mark. It is a highly dynamic feature of coastal systems. Shoreline fluctuations may have dramatic consequences at places where settlements are built close to the shore, as shown in Fig. 1. Coastal retreat and coastal erosion can be considered synonyms if the definitions of coastline and shoreline coincide. However, the term coastal erosion is generally understood as sand loss from the beach system, where the beach system includes the intertidal beach and often also the nearshore subtidal zone that frequently exchanges sand with the dry beach. In this case, the definition of the coastline is related to the sand volume of the entire beach system, see the article Coastline. The coastline is then a far more stable feature than the shoreline: shoreline retreat and coastal erosion are not synonymous.
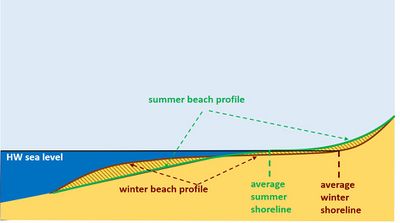
Shoreline variability usually has a seasonal component, see Fig. 2. The subaerial beach is higher and the lower beach slope steeper in summer than in winter. This seasonal pattern is more pronounced on reflective beaches than on dissipative beaches[2][3].
During winter, storm-related high water levels and energetic breaking waves transport sand from the backshore to the foreshore and even further offshore to the upper shoreface. The upper beach profile (and/or dune face) is steepened and the lower beach profile is flattened, implying an onshore shift of the shoreline. During summer, low-energy swell waves carry the sand deposited on the upper shoreface back to the subaerial beach. For tidal beaches, most sediment exchange takes place between the supratidal and lower-intertidal parts of the beach[2]. The distinction between summer and winter beach profiles does not apply to coasts subject to tropical cyclones that are more frequent in summer.
If incidental storms are not extremely severe, it is unusual (and confusing) to use the terms coastal erosion and coastal accretion for the seasonal fluctuation of the shoreline. The terms beach erosion and beach recovery are often used instead, especially in cases where the beach is backed by a natural or artificial hard structure.
Shoreline retreat
Shoreline retreat occurs when the beach is flooded by energetic breaking waves. These waves bring beach sand into suspension and produce strong undertow currents that evacuate beach sand to the upper shoreface and sometimes even further offshore. Several factors have been identified which contribute to the severity of coastal retreat.
- Beach exposure[4]. Highly exposed coastal stretches are typically oriented (close to) normal to the direction of the highest storm waves. High exposure also occurs when the shoreface slope is steep and natural or artificial protecting structures are absent: no rocky outcrops or shore platforms in the case of cliff coasts, no artificial breakwaters, etc. In some cases, erosion hotspots result from wave focusing through refraction over offshore bathymetric structures[5].
- Maximum wave run-up. Bergillos et al.[6] found that the maximum storm wave run-up is a more accurate indicator of storm wave erosion than the maximum wave height. There is also a strong relationship between shoreline retreat and the maximum storm surge level, which is a major component of the wave run-up[7].
- Antecedent beach state. The severity of shoreline retreat produced by a given storm surge depends on the time elapsed since the previous storm surge[8]. The impact of a storm surge cluster, a sequence of storm surges with intervals shorter than the time needed for recovery of the former shoreline, is greater than the impact of a single storm surge of similar magnitude[9]. However, the first storm in a cluster has greater impact than subsequent storms of similar magnitude. This suggests that the first storm has adjusted the beach profile such that it is better adapted to storm conditions[8]. A weaker single storm could thus have a larger impact than a stronger storm occurring in the middle of storm sequence. Hence, it is not possible to scale-up single-storm erosion studies into predictions of cluster-storm erosion[7].
Beaches situated on cliff coasts are often protected by a shore platform on which incident waves dissipate. Such beaches adapt to a low-energy equilibrium state until the occurrence of a high storm surge that inundates the platform and the subaerial beach. Massive erosion then occurs due to the combination of reflecting waves on the cliff and offshore transport of sand by backwash, undertow and rip currents[10]. Various combinations of tides, storm surge and waves can produce beach inundation and subsequent erosion.
In some situations, extreme storms can cause shoreline advance instead of shoreline retreat. This can happen in cases where beaches are backed by high sand dunes which supply sand to the beach while being eroded[2]. This sand is returned to the dune when conditions are favorable for aeolian sand transport from the beach to the dune. This is a slow process, however, in comparison with the rate of recovery of the original beach state. See also: Dune erosion and Dune development.
Temporary shoreline retreat can also occur without direct relationship with storm events. An example is the occurrence of migrating sand waves along the coast. Coastal sand waves are alongshore sequences of shoreline protrusions and embayments with wavelengths between 100 m and more than 10 km and amplitudes of ten to more than hundred meters. The generation mechanism is not always clear, but there is evidence that shoreline sand waves can arise from shoal migration across tidal inlets[11][12] or from shoreline instability under highly oblique wave incidence (see Rhythmic shoreline features#Large-scale shoreline features). The sand wave pattern can migrate alongshore by littoral drift; the migration rate is typically in the order of a few hundred meters per year in downdrift direction[13]. Migrating shoreline sand waves induce cyclic shoreline retreat and recovery which can have great impact on coastal settlements[14]. They probably play a role in the dramatic beach erosion at Saint Louis (Senegal) in March 2015 (see Fig. 1).
Shoreline recovery
In most cases the shoreline returns, at least partially, to its former position after storm-induced beach erosion. Shoreline recovery can be fast - weeks or months - although it always takes longer than storm-induced retreat[16]. Recovery can also be slow and take several years. Observations of beach recovery along SW England's cliff coast after the exceptional storms of the 2013-14 winter show that the fastest recovery rates occur for exposed beaches that have suffered greatest retreat; recovery rate and retreat rate appear to be positively correlated[4]. However, the most exposed beaches did not fully recover; the greatest net recovery after 3 years occurred for the semi-exposed coastal sections. Similar recovery periods have been recorded for foredune retreat by major storms on the Australian coast[17].
In other cases, observations show that post-storm accretion can be shifted by littoral drift to locations situated down-drift of the storm erosion sites[18].
Long-period waves (swell) provide a mechanism for returning sand from the subtidal and intertidal beach to the subaerial beach. Asymmetries in the wave-orbital velocity and acceleration, which develop when waves propagate into shallow water, play an important role, see Shoreface profile#Wave-induced onshore sediment transport. Shoreline recovery is significantly correlated with onshore migration of nearshore sandbarsCite error: Closing </ref> missing for <ref> tag. Fast shoreline recovery requires more energetic waves, but the steepness of these waves (essentially the ratio of wave height to wave length) should be significantly less than the steepness of the eroding storm waves[15]. Such conditions occur under moderate winter conditions or energetic summer conditions[19]. Substantial recovery can already be initiated at the waning of the storm.
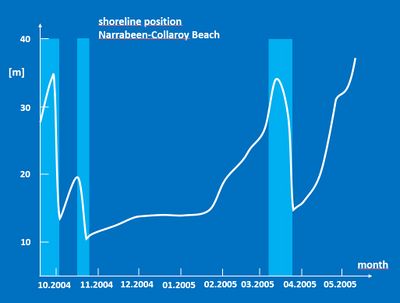
Fig. 3 shows after-storm recovery of the shoreline position at Narrabeen-Collaroy Beach in East Australia, near Sidney. The recovery period after each storm-induced shoreline retreat is a few months at this location. Welding of intertidal sandbars to the shore has been identified as a major mechanism for post-storm beach recovery on several beaches[20][21][22]. Whereas infragravity swash promote offshore transport during storms[23], observations on wide, gently sloping beaches show that they can also contribute to post-storm recovery[24]. Generally, beaches with an accretionary trend recover faster from storm erosion than stable or structurally eroding beaches.
It must be emphasized that shoreline recovery after storm erosion will not always occur. Recovery may not happen if the natural equilibrium conditions of the beach and shoreface are modified, for example due to human interventions that reduce the historical natural sand supply by longshore transport. Extreme storms can transport sand from the upper shoreface so far down the lower shoreface and towards the inner shelf, that onshore transport processes under more moderate wave conditions are not strong enough to bring the sand back[25].
Beach profile recovery
Recovery of the backshore (the dry beach from the beach berm to the dune foot) takes substantially longer than recovery of the shoreline position. Analysis of long-term beach profile records of a high-energy meso-macrotidal sandy beach showed that the slope of the lower beach (0-2 m above mean sea level) was variable at the storm time scale, while the slope of the upper beach (above the berm crest) was variable at the seasonal time scale[26]. Recovery of the full beach profile mainly proceeds through sand transport by swash uprush (wave run-up on the beach) during periods of high water levels (e.g. spring high water)[27]. Dune recovery is discussed more in detail in the article Dune erosion#Post-storm dune recovery.
Alongshore variability
Shoreline retreat (beach erosion) is site dependent and highly variable along the beach[19][28]. Eroding coastal stretches ('erosion hotspots') alternate with similar adjacent coastal stretches which are hardly affected during storms[18].
Several factors that may contribute to longshore variability in shoreline erosion are discussed elsewhere (see Rhythmic shoreline features): mega-cusps, related to high-angle wave-incidence instability; shoreline sand waves; shoreline embayments, related to intermittent shore-attachment of nearshore sandbars and rip cells. Exfiltration of groundwater and wave focussing through refraction over nearshore sandbanks are other possible causes of local erosion hotspots. However, the causes of alongshore variability in storm response are not always fully clear[18].
The fast natural recovery of beaches after storm-induced shoreline retreat suggests that the shoreline fluctuates around an equilibrium position in response to various alternating hydrodynamic conditions. This equilibrium shoreline position is generally not fixed, but gradually moves in onshore or offshore direction as a result of structural long-term processes of erosion or accretion. Based on observations of this long-term trend of the equilibrium shoreline position, a simple empirical model can be developed for shoreline prediction on different time scales. This is explained in the next paragraph. The effect of migrating longshore sand waves is not accounted for in this model, but can in principle be added.
Shoreline change prediction
Shoreline response to changing wave conditions can be very different depending on coastal typology, with even strong variations between nearby locations. Nevertheless, certain response characteristics are common to many beaches: the shoreline generally retreats under storm conditions and accretes under calm weather conditions. These shared characteristics can be modelled for each single location, providing a tool for local shoreline change prediction. The first ideas for such an approach were put forward by Wright, Short and Green[29] and later elaborated by Miller and Dean[30] and Yates, Guza and O'Reilly[31]. This shoreline response model is based on the following three assumptions:
- The shoreline location [math]X[/math] is at each time [math]t[/math] representative for a particular beach state;
- For each constant incident wave energy [math]E[/math], a unique equilibrium beach state exists, characterized by a shoreline position [math]X=X_{eq}[/math];
- When the wave energy is kept constant, the shoreline position [math]X(t)[/math] tends asymptotically to the equilibrium position [math]X_{eq}[/math].
It is questionable whether these conditions are always fulfilled; one may expect that for a given constant wave energy, different shoreline positions are possible. The equilibrium shoreline position may depend not only on wave energy, but also on wave incidence angle, longshore beach gradients and presence and location of nearshore sandbars. However, the approach based on the assumptions (1-3) is attractive due to its simplicity. The model can be applied to stable beaches (fluctuating around a long-term equilibrium), as well as to coasts with slow erosional or accretional trends, if the trend is known from observations.
The evolution of the shoreline position towards the equilibrium position is assumed to follow the linear relaxation law
[math]dX/dt = k(E) ( X_{eq} - X) , \quad X_{eq} = f(E) . \qquad (1)[/math]
Because the equilibrium shoreline position retreats for increasing values of [math]E[/math], the function [math]f[/math] should be a decreasing function of [math]E[/math]. It can be parameterized by a linear relationship [math] f(E) = (b - E)/a[/math], as shown by Yates et al.[31]. The factor [math]k(E)[/math] is an increasing function of [math]E[/math], because shoreline retreat under high waves is a faster process than shoreline accretion under calm conditions; it can be modeled as [math]k(E) = aC^{\pm} E^n[/math], where [math]C^+[/math] applies for retreat ([math]E \gt b - aX[/math]) and [math]C^-[/math] for accretion ([math]E \lt b-aX [/math]). The parameters [math]a, b, C^{\pm}[/math] are determined by fitting Eq. 1 to records of observed shoreline positions [math]X(t)[/math] and wave energies [math]E(t)[/math]. Such records should have sufficient temporal resolution and length.
Fair estimates of observed shoreline change could be produced with this model for several field situations[31][32]. The exponent was taken as [math]n=1/2[/math], but the precise value was not essential for the results. The values found for the parameters [math]C^+[/math] and [math]C^-[/math] were not very different.
The parameters [math]a, b, C^{\pm}[/math] in the model Eq. (1) are constants. A refinement of the model was proposed by Long and Plant (2012[33]) with the incorporation of a trend term and a Kalman filter algorithm which continuously updates the parameter values and provides uncertainty estimates identifying confidence of the forecasts and parameter estimates. The Kalman filter algorithm yields improved predictions in cases where the equilibrium shoreline varies due to natural or man-induced processes that are not linearly related to [math]E[/math].
Instead of [math]E[/math], other beach state indicators are possible. Davidson et al. (2013[34]) developed a similar shoreline prediction model with only three adjustable parameters. As it appeared that the performance of the model based on [math]E[/math] exhibited a dependence on the beach grainsize, these authors used the Dean parameter [math]\Omega = H_s/(wT_p)[/math] to represent the beach state (see Appendix). They further considered that different values of the parameter [math]\Omega[/math] correspond to different types of shoreface profiles, as shown by Wright and Short (1984[35]) for Australian beaches and verified afterwards for many beaches worldwide. In this model, accretion or erosion depends linearly on the deviation of the instantaneous [math]\Omega[/math] from an antecedent 'equilibrium' beach state indicator [math]\Omega^{(\Phi)}[/math]. This indicator is represented by a weighted average of previous beach states [math]\Omega[/math] with memory time scale [math]\Phi[/math]. It therefore depends on the shoreface profile that has evolved in the course of time and circumvents the second condition (2). Shoreline prediction with this model was shown to be successful for many beaches[34][36].
The above shoreline prediction models are restricted to beaches where shoreline change is dominated by cross-shore processes. They are less suited for beaches where shoreline change is influenced by long-shore processes, as the beach state parameter [math]\Omega[/math] is not an indicator for changes in longshore transport gradients, due, for instance, to changing wind directions.
Shoreline prediction as management tool
Shoreline change prediction models are useful tools for coastal management and planning. Systematic comparison of predicted shoreline retreat with observations provides a means to distinguish temporary fluctuations from trends in shoreline position. This is necessary for planning shoreline maintenance interventions, such as beach or shoreface nourishments. Shoreline prediction models can also be used for establishing shoreline retreat statistics and for estimating the recurrence of extreme retreat events[37]. This is crucial for defining hazard zones where construction is regulated (or simply forbidden, see Setback area). Reliable estimates require long time series of observed shoreline positions for tuning the model parameters. Such time series can be obtained from satellite images. Using satellite derived shorelines for Truc Vert beach (Aquitaine, France) it was shown that even data which are not corrected for tide level and wave conditions provided input to the shoreline prediction model of comparable quality as time series of in situ measured shorelines[38]. The quality of the model prediction improved with alongshore averaging of the satellite derived shoreline positions and further depended on the sampling frequency (more than once a month) and the duration (more than 4 years) of the time series.
Appendix
The shoreline prediction model of Davidson et al. (2013[34]) uses the equation:
[math]X_k = X_{k-1} + \Big[ C^{\pm} \sqrt{P_k} \Large\frac{\Omega_k - \Omega_k^{(\Phi)}}{\sigma}\normalsize + b \Big] \Delta t \qquad (A1)[/math].
The symbols have the following meaning:
[math]X_k[/math] is the shoreline position at time [math]t=k\Delta t[/math] at a particular fixed location along the coast.
[math]P_k[/math] is the wave power at time [math]t=k\Delta t[/math], computed as [math]P = \frac{1}{16} g \rho \sqrt{g h_b} H_{s, b}^2 , \;[/math] where [math]\rho[/math] is the seawater density, [math]g[/math] is the gravitational acceleration, [math]h_b[/math] is the depth at the wave breaking location, [math]H_{s,b}[/math] is the significant wave height at the breaking location.
[math]\Omega_k[/math] is the value of the Dean-parameter [math]\Omega=\Large\frac{H_{s,b}}{wT}[/math] at time [math]t=k\Delta t[/math],
[math]w[/math] is the mean sediment fall velocity, [math]T[/math] is the spectral peak wave period.
[math]\Omega_k^{(\Phi)}[/math] represents the time-varying equilibrium beach state, [math]\Omega_k^{(\Phi)} = \sum_{n=1}^{n=2 \Phi} \Omega_{k-n} e^{-n/\Phi} / \sum_{n=1}^{n=2 \Phi} e^{-n/\Phi} ,[/math]
[math]\Phi[/math] is the memory time scale of the beach system.
[math]\sigma[/math] is the standard deviation of [math]\Omega[/math] over the whole observation record.
[math]C^+ =C[/math] is an adjustable parameter, used in Eq. (A1) for accretionary time steps [math](\Omega_k - \Omega_k^{(\Phi)})\gt 0[/math].
[math]C^- = r C[/math], is used in Eq. (A1) for erosional time steps [math](\Omega_k - \Omega_k^{(\Phi)})\lt 0 ,[/math]
[math]r[/math] is the erosion rate that reflects the different time scales of accretionary and erosional processes; it is computed as
[math]r= - \Large\frac{\lt \sqrt{P_k} (\Omega_k - \Omega_k^{(\Phi)})\gt ^+}{\lt \sqrt{P_k} (\Omega_k - \Omega_k^{(\Phi)})\gt ^-} [/math], where [math]\lt …\gt ^+[/math] is the average of all accretionary steps, [math](\Omega_k - \Omega_k^{(\Phi)})\gt 0[/math], taken over the whole observation record, and [math]\lt …\gt ^-[/math] is the average over all erosional steps, [math](\Omega_k - \Omega_k^{(\Phi)}) \lt 0[/math].
[math]b[/math] is a parameter representing the long-term trend in erosion or accretion, related, for instance, to persistent gradients in littoral drift or sea level rise.
The model has three adjustable parameters, [math]C[/math], [math]\Phi[/math] and [math]b[/math], that are fitted to the observation record of shoreline positions at a particular fixed location along the coast.
Related articles
- Shoreface profile
- Bruun rule
- Coastline
- Active coastal zone
- Erosion hotspots
- Dune erosion
- Dune development
- Dealing with coastal erosion
- Human causes of coastal erosion
- Natural causes of coastal erosion
- Nearshore sandbars
References
- ↑ Hapke, C.J., Kratzmann, M.G. and Himmelstoss, E.A. 2013. Geomorphic and human influence on large-scale coastal change. Geomorphology 199: 160-170
- ↑ 2.0 2.1 2.2 Quartel, S., Kroon, A. and Ruessink, B.G. 2008. Seasonal accretion and erosion patterns of a microtidal sandy beach. Mar. Geol. 250: 19-33
- ↑ Poate, T., Masselink, G., Russell, P. and Austin, M. 2014. Morphodynamic variability of high-energy macrotidal beaches, Cornwall, UK. Marine Geol. 350: 97-111
- ↑ 4.0 4.1 Konstantinou, A., Stokes, C., Masselink, G. and Scott, T. 2021. The extreme 2013/14 winter storms: Regional patterns in multi-annual beach recovery. Geomorphology 389, 107828
- ↑ Healy, T.R. 1987. The importance of wave focusing in the coastal erosion and sedimentation process. Proceed. Coastal Sediments ’87. American Society of Civil Engineering, New York, pp. 1472–1485
- ↑ Bergillos, R.J., Masselink, G. and Ortega-Sánchez, M. 2017. Coupling cross-shore and longshore sediment transport to model storm response along a mixed sand-gravel coast under varying wave directions. Coast. Eng. 129: 93–104
- ↑ 7.0 7.1 Castelle, B., Marieu, V., Bujan, S., Ferreira, S., Parisot, J.P., Capo, S., Senechal, N. and Chouzenoux, T. 2014. Equilibrium shoreline modelling of a high energy meso-macro-tidal multiple-barred beach. Mar. Geol. 347: 85–94 Cite error: Invalid
<ref>tag; name "C14" defined multiple times with different content - ↑ 8.0 8.1 Angnuureng, D.B., Almar, R., Senechal, N., Castelle, B., Addo, K.A., Marieu, V. and Ranasinghe, R. 2017. Shoreline resilience to individual storms and storm clusters on a meso-macrotidal barred beach. Geomorphology 290: 265–276
- ↑ Ciavola, P. and Stive, M.J.F. 2012. Thresholds for storm impacts along European coastlines: Introduction. Geomorphology 143-144: 1-2
- ↑ Bastos, A.P., Taborda, R., Silva, A.N., Lira, C.P., Andrade, C. and Calvao, J.M. 2022. A punctuated equilibrium model for storm response of geologically controlled beaches: Application to western Portuguese beaches. Geomorphology 404, 108184
- ↑ Sha, L.P. 1989. Variation in ebb-delta morphologies along the West and East Frisian islands, the Netherlands and Germany. Marine Geology 89: 11-28
- ↑ Cayocca, F. 2001. Long-term morphological modeling of a tidal inlet: the Arcachon Basin, France. Coastal Engineering 42: 115–142
- ↑ Van den Berg, N., Falques, Q. and Ribas, F. 2012. Modeling large scale shoreline sand waves under oblique wave incidence. Journal Geophysical Res. 117, F03019
- ↑ Stive, M. J. F., Aarninkhof, S. G. J. Hamm, L. Hanson, H. Larson, M., Wijnberg, K. M., Nicholls, R. J. and Capobianco, M. 2002. Variability of shore and shoreline evolution. Coastal Eng. 47: 211–235
- ↑ 15.0 15.1 Phillips, M.S., Harley, M.D., Turner, I.L., Splinter, K.D. and Cox, R.J. 2017. Shoreline recovery on wave-dominated sandy coastlines: the role of sandbar morphodynamics and nearshore wave parameters. Mar. Geol. 385: 146–159
- ↑ Wright, L.D. and Short, A.D. 1984. Morphodynamic variability of surf zones and beaches: a synthesis. Mar.Geol. 56: 93-118
- ↑ McLean, R., Thom, B., Shen, J. and Oliver, T. 2023. 50 years of beach–foredune change on the southeastern coast of Australia: Bengello Beach, Moruya, NSW, 1972–2022. Geomorphology 439, 108850
- ↑ 18.0 18.1 18.2 List, J.H., Farris, A.S. and Sullivan, C. 2006. Reversing storm hotspots on sandy beaches: Spatial and temporal characteristics. Mar. Geology 226: 261- 279
- ↑ 19.0 19.1 Dodet, G., Castelle, B., Masselink, G., Scott, T., Davidson, M., Floc’h, F., Jackson, D. and Suanez, S. 2019. Beach recovery from extreme storm activity during the 2013–14 winter along the Atlantic coast of Europe. Earth Surf. Process. Landf. 44: 393–401
- ↑ Castelle, B., Ruessink, B. G., Bonneton, P., Marieu, V., Bruneau, N., and Price, T. D. 2010. Coupling mechanisms in double sandbar systems, Part 1: Patterns and physical explanation. Earth Surf. Proc. Landforms 35: 476-486
- ↑ Brooks, S.M., Spencer, T. and Christie, E.K. 2017. Storm impacts and shoreline recovery: Mechanisms and controls in the southern North Sea. Geomorphology 283: 48–60
- ↑ Montreuil A.-L., Chena, M., Branda, E., Verwaest, T. and Houthuys, R. 2020. Post-storm recovery assessment of urbanized versus natural sandy macro-tidal beaches and their geomorphic variability. Geomorphology 356, 107096
- ↑ Pontiki, M., Puleo, J. A., Bond, H., Wengrove, M., Feagin, R. A., Hsu, T.-J. and Huff, T. 2023. Geomorphic response of a coastal berm to storm surge and the importance of sheet flow dynamics. Journal of Geophysical Research: Earth Surface 128, e2022JF006948
- ↑ Cohn, N., Ruggiero, P., Garcia-Medina, G., Anderson, D., Sefarin, K.A. and Biel, R. 2019. Environmental and morphologic controls on wave-induced dune response. Geomorphology 329: 108–128
- ↑ Guillen, J., Simarro, G., Calvete, D., Ribas, F., Fernandez-Mora, A., Orfila, A., Falques, A., de Swart, R., Sancho-García, A. and Duran, R. 2024. Sediment leakage on the beach and upper shoreface due to extreme storms. Marine Geology 468, 107207
- ↑ Labarthe, C., Castelle, B., Marieu, V., Garlan, T. and Bujan, S. 2023. Observation and Modeling of the Equilibrium Slope Response of a High-Energy Meso-Macrotidal Sandy Beach. J. Mar. Sci. Eng. 11, 584
- ↑ Phillips, M. S., Blenkinsopp, C. E., Splinter, K. D., Harley, M. D. and Turner, I. L. 2019. Modes of berm and beachface recovery following storm reset: Observations using a continuously scanning lidar. Journal of Geophysical Research: Earth Surface 124: 720–736
- ↑ Scott, T., Masselink, G., O’Hare, T., Saulter, A., Poate, T., Russell, P., Davidson,M. and Conley, D. 2016. The extreme 2013/2014 winter storms: beach recovery along the southwest coast of England. Mar. Geol. 382: 224–241
- ↑ Wright, L. D., Short, A. D. and Green, M. O. 1985. Short-term changes in the morphodynamic states of beaches and surf zones: An empirical predictive model. Marine Geol., 62: 339- 364
- ↑ Miller, J. K. and Dean, R. G. 2004. A simple new shoreline change model. Coastal Eng. 51: 531- 556
- ↑ 31.0 31.1 31.2 Yates, M. L., Guza, R. T. and O’Reilly W. C. 2009. Equilibrium shoreline response: Observations and modelling. J. Geophys. Res. 114: C09014, doi:10.1029/2009JC005359
- ↑ Yates, M. L., Guza, R. T., O’Reilly W. C., Hansen, J.E. and Barnard, P.L. 2011
- ↑ Long, J.W. and Plant, N.G. 2012. Extended Kalman Filter framework for forecasting shoreline evolution. Geophysical Research Letters 39, L13603
- ↑ 34.0 34.1 34.2 Davidson, M.A., Splinter, K.D. and Turner, I.L. 2013. A simple equilibrium model for predicting shoreline change. Coastal Eng. 73: 191-202
- ↑ Wright, L. D. and A. D. Short 1984. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 56: 93–118
- ↑ Splinter, K.D., Turner, I.L., Davidson, M.A., Barnard, P., Castelle, B. and Oltman-Shay, J. 2014. A generalized equilibrium model for predicting daily to interannual shoreline response. Journal of Geophysical Research-Earth Surface 119: 1936–1958
- ↑ Davidson, M.A., Turner, I.L., Splinter, K.D. and Harley, M.D. 2017. Annual prediction of shoreline erosion and subsequent recovery. Coastal Engineering 130: 14–25
- ↑ Azorakos, G., Castelle, B., Marieu, V. and Idier, D. 2024. Satellite-derived equilibrium shoreline modelling at a high-energy meso-macrotidal beach. Coastal Engineering 191, 104536
Please note that others may also have edited the contents of this article.
|