Breaker index
The process of wave breaking plays a crucial role in the morphodynamics of the shoreface and the beach, such as accretion or erosion trends and the development and dynamics of nearshore bars and rip currents. The breaker index concept has been introduced to estimate the location on the shoreface where wave breaking occurs based on empirical formulas, without the need for a detailed simulation of the breaker process.
Contents
A practical wave breaking criterion
According to numerical simulations[1] and flume experiments[2], wave breaking starts on the shoreface when the horizontal surface water particle velocity at the wave crest comes close (within about 15%) to the wave crest celerity of the tallest wave in the incident wave train. However, it is not easy to derive from this criterion at which location on the shoreface wave breaking will occur. Even if the characteristics of the incident waves and the shoreface profile are well known, one has to face the problem that wave breaking is highly sensitive to fine-scale processes. It cannot be easily modelled, although significant progress has been achieved with numerical techniques such as Computational Fluid Dynamics (CFD)[3] or Smoothed Particle Hydrodynamics (SPH)[4]. For this reason, many investigations have been conducted to establish empirical rules for wave breaking from which the location of wave breaking can be easily derived. These empirical rules refer to the so-called breaker index. The breaker index relates the wave height at breaking, [math]H_b[/math], to the water depth [math]h_b[/math] at the breakpoint; it is defined as
[math]\gamma_b=H_b/h_b . \qquad (1)[/math]
Important parameters for the wave breaking process are the steepness [math]H_0/L_0[/math] of the incident waves ([math]H_0, L_0[/math] are the offshore wave height and wavelength) and the average shoreface slope [math]m[/math]. Empirical rules establish a relationship between the breaker index and these parameters.
Wave breaking process
The process of wave breaking starts on the shoaling zone where incident waves become progressively skewed by interaction with the seabed: the wave crest becomes sharper and higher, while the wave trough widens and flattens (Fig. 1). Incident waves with short wavelengths (locally generated 'sea') are steeper than incident waves with longer wavelengths (remotely generated swell); the former category of waves will break earlier, thus at greater depth [math]h_b[/math] than the latter category[3][5], implying a smaller value of [math]\gamma_b[/math] [6]. These short sea waves are also less skewed before breaking; they break when the crest becomes unstable and flows down the front face of the wave, producing spilling breaker bores that surf towards the shoreline (Fig. 2). This breaking mode is also favoured on gently sloping shorefaces when the surf similarity parameter [math]\xi=m/\sqrt{H_0/L_0}[/math] (ratio of shoreface slope and square root of offshore wave steepness) has values typically smaller than about 0.4. Incident waves with longer wavelengths will break later, thus at smaller depth [math]h_b[/math]. While shoaling, they are strongly skewed and break when the crest curls over the front face and falls into the base of the wave, producing a so-called plunging breaker[7] (Fig. 3). This breaking mode is also favoured on steep sloping shorefaces when the surf similarity parameter has values typically larger than 0.4. Direct measurements give an approx. 20% larger breaker index for plunging waves compared to spilling waves[8][9].
Wave breaking formulas (regular waves)
Analytical formulas for the breaker index have been derived from laboratory experiments, field observations and numerical simulation models. Reviews of the various methods and formulas have been given by Camenen and Larson (2007[7]) and Robertson et al. (2013[10]). Most formulas involve the steepness [math]H_0/L_0[/math] of the incident wave and the average seabed slope [math]m[/math] and reproduce the qualitative tendencies described above, i.e. [math]\gamma_b[/math] is an increasing function of the wave steepness and the seabed slope.
A theoretical limit for [math]\gamma_b[/math] was established by Miche (1944[12]), who analysed the wave motion over a horizontal seabed to determine the maximum crest steepness of the incident wave before collapse (occurring when the surface fluid velocity equals the wave crest celerity). Using a second-order theory of small-amplitude wave propagation, Miche found
[math]\Large\frac{H_b}{L_b}\normalsize \lt 0.14 \, \tanh(k_b \, h_b) \quad[/math] or [math]\quad \gamma_b \lt \Large\frac{0.88}{k_b \, h_b}\normalsize \tanh(k_b\, h_b) , \quad k_b=2 \pi / L_b , \qquad (2)[/math]
where [math]L_b[/math] is the wavelength at the breakpoint. Field observations[9] and detailed numerical modeling[13] indicate that wave crests already break with a steepness value [math]H_b/L_b[/math] smaller than Miche's limiting criterion.
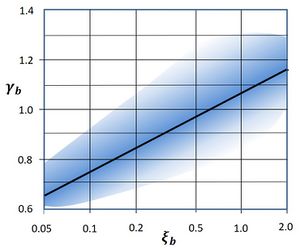
Experiments by Battjes (1974[14]) suggested that the dependence of [math]\gamma_b[/math] on wave steepness and bed slope could be represented by the surf similarity parameter [math]\xi[/math] at the breakpoint,
[math]\gamma_b = 1.06 + 0.14 \ln \xi_b . \qquad (3)[/math]
Another frequently used formula was established by Goda (2010[5])
[math]\gamma_{b} = 0.17 \Large\frac{L_0}{h_{b}}\normalsize \Big[1-\exp\big(-\Large\frac{3 \pi}{2}\frac{h_{b}}{L_0}\normalsize (1+11m^{4/3})\big)\Big]. \qquad (4)[/math]
This formula requires an iterative solution because of the dependence on [math]h_b[/math]. Goda's formula overestimates the breaker index for [math]h_b/L_0 \gt 0.1[/math] [15].
The results of experiments designed to determine the breaker index yield widely scattered results, even for experiments with similar bed slope and incident waves. Fig. 4 gives an impression of the range covered by experimental data when the breaker index is plotted as a function of the surf similarity parameter. Although the scatter can be partly explained by the dependence of the breaker index on other parameters besides [math]\xi[/math], it also suggests that the breaking process should be considered a stochastic process that is very sensitive to small factors that are not accounted for in the gross characteristics of the experimental setup[5].
Irregular waves
The formulas (2-4) were derived for regular monochromatic waves. However, incident wave trains in nature usually have an irregular, random character. An irregular wave field can be characterized by a wave spectrum with root-mean-square wave height [math]H_{rms}[/math] (see Statistical description of wave parameters). Since individual waves in a wave train have different breakpoints in the surf zone, the breaker index concept cannot be applied as such for [math]H_{rms}[/math]. This problem can be addressed in two ways. The first way is to consider the breaking of individual waves in an incident wave train, represented by a wave-by-wave breaker index. The second way is to consider the location in the surf zone where [math]H_{rms}[/math] starts to decay (the intersection of the shoaling zone where [math]H_{rms}[/math] increases and the surf zone where [math]H_{rms}[/math] decreases[16]); this location is called the incipient breakpoint, indicated by the subscript [math]ib[/math]. The wave-by-wave breaker index is similar the breaker index for regular waves[17]. The incipient breaker index [math]\gamma_{ib}[/math] is significantly smaller than the breaker index for regular waves, but the dependence on wave steepness and bed slope is similar. The empirical formulas for regular waves can be applied for irregular waves if the value of [math]\gamma_b[/math] is reduced by about 50% [11][17]. According to Goda (2010[5]), at incipient breaking (subscript [math]ib[/math]):
[math]\gamma_{ib} \equiv \Large\frac{H_{rms,ib}}{h_{ib}}\normalsize = 0.084 \Large\frac{L_0}{h_{ib}}\normalsize \Big[1-\exp\big(-\Large\frac{3 \pi}{2}\frac{h_{ib}}{L_0}\normalsize (1+11m^{4/3})\big)\Big] . \qquad (5)[/math]
Wave decay in the surf zone
After initial breaking the wave propagates shoreward, often as a bore, while decreasing in height. The decay of the wave height [math]H(x)[/math] can be derived from the equation:
[math] gradient \; of \; wave \; energy \; flux = wave \; energy \; dissipation, \qquad (6)[/math]
in which for both terms explicit expressions as function [math]H(x)[/math] have to be substituted. The wave energy dissipation depends on several factors, including the proportion of broken waves in the surf zone. If all waves are broken, the surf zone is said to be saturated, but for an irregular (random) wave field this is generally not the case. Explicit expressions for the terms in Eq. (6) have been proposed by Battjes and Janssen (1978[18]) and Baldock et al. (1998[19]), but they rely on several assumptions (see the Appendix).
Many laboratory and field investigations have therefore been conducted to establish empirical relationships for the dependence of the wave height [math]H(x)[/math] on the local water depth [math]h(x)[/math] in the surf zone. The simplest relationship is a constant ratio of wave height and water depth in the surf zone,
[math]\Large\frac{H(x)}{h(x)}\normalsize = \gamma_b . \qquad (7)[/math]
Flume experiments suggest that this relationship is satisfied to some extent for rather steep shoreface profiles ([math]m \approx 1/30[/math]), but not for more gently sloping shorefaces[20]. For more gently sloping profiles the ratio [math]H/h[/math] displays a notable increase at small water depths[21][5][17][22]. This may be due to wave regeneration after breaking, which commonly occurs in the troughs between nearshore sandbars. These regenerated waves propagate shoreward with less energy loss than broken wave bores. For an irregular wavefield, the increase in [math]H_s/h[/math] may also be due to a large percentage of waves that have not yet broken past the incipient breakpoint; the proportion of these shoaling waves (still increasing in height) gradually decreases as the wave train travels towards the coast[5][17].
The assumption that the wave height depends on the local depth can be justified if the surf zone depth decreases monotonically towards the shoreline, with an approximately constant slope [math]m[/math]. In other situations there is no reason to assume such a dependence[18]. For example, for a wave propagating across a surf zone with nearshore sandbars, the wave height at the trough between sandbars depends on the crest height of the previous sandbar.
Appendix Surf zone decay irregular waves
Wave energy dissipation in the surf zone can be described by Eq. (6),
[math]\Large\frac{dP}{dx}\normalsize + D =0 , \qquad (A1)[/math]
where the [math]x[/math]-axis points towards the local shoreline. In linear wave theory the wave energy flux [math]P[/math] can be approximated by
[math]P= \frac{1}{8} \rho g H_{rms}^2 c_g \cos \overline \theta , \qquad (A2)[/math]
where [math]g[/math] is the gravitational acceleration, [math]\rho[/math] the seawater density, [math]\overline \theta[/math] the mean incident wave direction and [math]c_g[/math] the wave group velocity, which in shallow water is about equal to the wave propagation speed [math]c \approx \sqrt{gh}[/math].
Analyses of field experiments indicate that, in general, wave dissipation in the surf zone is primarily due to wave breaking, with only a minor contribution of frictional loss[23]. An expression for the energy dissipation [math]D[/math] by breaking waves was derived by Battjes and Janssen (1978[18]) based on analogy with the power dissipated by a bore,
[math]D \approx Q_b \rho g \Large\frac{H^3}{4hT}\normalsize , \qquad (A3)[/math]
where [math]Q_b[/math] the fraction of broken waves in the surf zone, [math]T[/math] is thepeak wave period, and [math]H[/math] the height of an individual wave. [For a derivation, see Tidal bore dynamics Eq. (5) with: [math]\; D = \Large\frac{Q \Delta E}{L}\normalsize = - \Large \frac{\rho g}{4L} \frac{v_2}{D_1}\normalsize (D_2 – D_1)^3, \quad D_1=h, \; D_2 - D_1=H, \; v_2 = - \sqrt{gh}\sqrt{\Large\frac{H+2h}{2 (H+h)}\normalsize} \approx - \sqrt{gh}= -\Large\frac{L}{T}\normalsize \, , \;[/math] where [math]L=[/math] wavelength ]
Baldock et al. (1998[19]) and Janssen and Battjes (2007[24]) derived an analytical expression for [math]Q_b[/math] by assuming a Rayleigh distribution of the incident waves (see Statistical description of wave parameters). The following expression for the wave energy dissipation is found:
[math]D = \rho g \Large\frac{H_{rms}^3}{4hT}\normalsize \; \Big[(R^3 + \frac{3}{2} R) \exp(-R^2) \, + \, \Large\frac{3 \sqrt{\pi}}{4}\normalsize \, (1-erf(R)) \Big] \approx \rho g \, \Large\frac{H_{rms}^2}{4T}\normalsize \, (1+R^2) \, \exp(-R^2) , \quad R=\Large\frac{H_b}{H_{rms}}\normalsize, \qquad (A4)[/math]
where the approximation holds for gently sloping surf zone profiles ([math]m\lt 0.01[/math]) and where [math]erf[/math] is the error function. The expression (A4) represents wave dissipation by breaking waves. Dissipation by other processes such as energy dissipation due to bottom friction and energy transfer to infragravity waves are usually small but need to be considered in specific situations.
An expression of the breaker wave height in the surf zone [math]H_b(x)[/math] was derived by Battjes and Janssen (1978[18]) based on Miche's criterion,
[math]H_b=\Large\frac{0.88}{k}\normalsize \tanh(\large\frac{\gamma}{0.88}\normalsize kh) , \qquad (A5)[/math]
where [math]k=2 \pi / (cT)[/math] is the wave number. In shallow water ([math]kh \lt \lt 1[/math]), the breaker wave height [math]H_b \approx \gamma h[/math]. The breaker index [math]\gamma[/math] should not be confused with [math]\gamma_b[/math] (Eq. 1).
Different empirical relationships have been established for the breaker index [math]\gamma[/math] defined by equation (A5), by solving Eq. (A1) and comparing the results with data from laboratory experiments and field surveys. Battjes and Stive (1985[25]) found a linear dependence of [math]\gamma[/math] on the offshore wave steepness [math]S_0=H_0/L_0[/math] for small values of [math]S_0[/math], Apotsos et al. (2008[26]) found a linear dependance on the offshore wave height [math]H_0[/math] for small values of [math]H_0[/math], whereas Ruessink et al. (2003[27]) found that the breaker index for beaches with nearshore sandbars depends on [math]kh[/math]. Analyzing a large set of field data, Zhang et al. (2021[28]) found that [math]\gamma[/math] is an increasing function of [math]kh[/math] for large values of the offshore wave steepness [math]S_0[/math], and a decreasing function of [math]kh[/math] for smaller offshore wave steepness, according to the empirical formula, valid for [math]0\lt S_0\lt 0.05[/math] and [math]0.3\lt kh\lt 1.2[/math]:
[math]\gamma = (237 \, S_0^2-34.8 \, S_0 +1.46) \, \exp \big(1.96 \, kh \, \ln(38.64 \, S_0)\big) . \qquad (A6)[/math]
Related articles
- Shoreface profile
- Shallow-water wave theory
- Wave transformation
- Surf similarity parameter
- Waves
- Wave set-up
- Littoral drift and shoreline modelling
References
- ↑ Barthelemy, X., Banner, M., Peirson, W., Fedele, F., Allis, M. and Dias, F. 2018. On a unified breaking onset threshold for gravity waves in deep and intermediate depth water. Journal of Fluid Mechanics 841: 463-488
- ↑ Saket, A., Peirson, W., Banner, M., Barthelemy, X. and Allis, M. 2017. Wave breaking onset of two-dimensional deep-water wave groups in the presence and absence of wind. J. Fluid Mech. 811: 642–658
- ↑ 3.0 3.1 Aggarwal, A., Chella, M.A., Bihs, H. and Myrhaug, D. 2020. Properties of breaking irregular waves over slopes. Ocean Engineering 216, 108098
- ↑ Lowe, R.J., Buckley, M.L., Altomare, C., Rijnsdorp, D.P., Yao, Y., Suzuki, T. and Bricker, J.D. 2019 Numerical simulations of surf zone wave dynamics using Smoothed Particle Hydrodynamics. Ocean Modelling 144, 101481
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Goda, Y. 2010. Reanalysis of regular and random breaking wave statistics. Coastal Engineering Journal 52: 71-106
- ↑ Xu, J., Liu, S., Li, J. and Jia, W. 2021. Experimental study of wave height, crest, and trough distributions of directional irregular waves on a slope. Ocean Engineering 242: 110136
- ↑ 7.0 7.1 Camenen, B. and Larson, M. 2007. Predictive Formulas for Breaker Depth Index and Breaker Type. Journal of Coastal Research 23: 1028–1041
- ↑ Weishar, L. L. and Byrne, R. J. 1978. Field study of breaking wave characteristics. In Procs. Coastal Eng. Conf. 1978, ASCE, pp. 487–506
- ↑ 9.0 9.1 Carini, R. J., Chickadel, C. C. and Jessup, A. T. 2021. Surf zone waves at the onset of breaking: 2. Predicting breaking and breaker type. Journal of Geophysical Research: Oceans 126, e2020JC016935
- ↑ Robertson, B., Hall, K., Zytner, R. and Nistor, I. 2013. Breaking waves: review of characteristic relationships. Coastal Engineering Journal 55(1), 1350002
- ↑ 11.0 11.1 Ostendorf, D. and Madsen, O. 1979. An Analysis of Longshore Current and Associated Sediment Transport in the Surf Zone. Boston: Massachusetts Institute of Technology, Department of Civil Engineering Technical Report 241, 169p.
- ↑ Miche, R. 1944. Mouvements ondulatoires de l’océan pour une eau profonde constante et décroissante. Annales des Ponts et Chaussées 114: 369-406
- ↑ Derakhti, M., Kirby, J. T., Banner, M. L., Grilli, S. T. and Thomson, J. 2020. A unified breaking onset criterion for surface gravity water waves in arbitrary depth. Journal of Geophysical Research: Oceans 125: 1–28
- ↑ Battjes, J.A. 1974. Surf similarity. Proceedings 14th International Conference on Coastal Engineering, pp. 466–480
- ↑ Kim, M., Lee, S. and Hong, J-W. 2022. Empirical estimation of the breaker index using a stereo camera system. Ocean Engineering 265, 112522
- ↑ Kamphuis, J. W. 1991. Incipient wave breaking. Coastal Engineering 15: 185–203
- ↑ 17.0 17.1 17.2 17.3 Xu, J., Liu, S., Li, J. and Jia, W. 2020. Experimental study of breaker index of normal and oblique incident unidirectional and multidirectional irregular waves on slope. Ocean Engineering 213, 107792
- ↑ 18.0 18.1 18.2 18.3 Battjes, J.A. and Janssen, J.P.F.M. 1978. Energy loss and set-up due to breaking of random waves. Proc. 16th Int. Conf. on Coastal Engineering. ASCE, New York, pp. 570–587
- ↑ 19.0 19.1 Baldock, T.E., Holmes, P., Bunker, S. and Van Weert, P. 1998. Crossshore hydrodynamics within an unsaturated surf zone. Coast. Eng. 34: 173–196
- ↑ Dally, W. R., Dean, R. G. and Dalrymple, R. A. 1985. A model for breaker decay on beaches. Proc. 19th Int. Conf. on Coastal Engineering, Vol. 1, pp. 82–98
- ↑ Raubenheimer, B., Guza, R. T. and Elgar, S. 1996. Wave transformation across the inner surf zone. J. Geophys. Res. 101(C11): 25,589–25,597
- ↑ Power, H. E., Hughes, M. G., Aagaard, T. and Baldock, T. E. 2010. Nearshore wave height variation in unsaturated surf. J. Geophys. Res. 115, C08030
- ↑ Thornton, E.B. and Guza, R.T. 1983. Transformation of wave height distribution. J. Geophys. Res. 88: 5925-5938
- ↑ Janssen, T.T. and Battjes, J.A. 2007. A note on wave energy dissipation over steep beaches. Coastal Engineering 54: 711–716
- ↑ Battjes, J. A. and Stive , M. J. F . 1985. Calibration and verification of a dissipation model for random breaking waves. Journal of Geophysical Research: Oceans 90: 9159-9167
- ↑ Apotsos, A., Raubenheimer, B., Elgar, S. and Guza, R. 2008. Testing and calibrating parametric wave transformation models on natural beaches. Coast. Eng. 55: 224–235
- ↑ Ruessink, B.G., Walstra, D.J.R. and Southgate, H.N. 2003. Calibration and verification of a parametric wave model on barred beaches. Coastal Eng. 48: 139–149
- ↑ Zhang, C., Li, Y., Cai, Y., Shi, J., Zheng, J., Cai, F. and Qi, H. 2021. Parameterization of nearshore wave breaker index. Coast Eng. 168, 103914
Please note that others may also have edited the contents of this article.
|


