Waves and currents by X-band radar

From Coastal Wiki
Jump to: navigation, search

This article describes how X-band radar can be used to obtain several sea state parameters. X-band radar is an example of a remote sensing technique. This article starts with an introduction of the measurement technique. Furthermore it explains how obtained data can be used to generate a required output.

Introduction

Many offshore operations are critically dependent on the prevailing sea state. To enhance the safety of crew, vessels, buildings and environment, reliable sea state measurements are required. In coastal areas, sea state measurements are needed to support weather, wave climate and ship routing services. Wave data is essential for the protection of the coastal zone to estimate the eroding forces of wind, waves, and currents. Due to climate change and its impact on coastal protection, wave and current measurements are of growing importance.

In the last decades, a broad range of new measurement systems was developed to extend the scope of traditional equipment like wave rider buoys. Especially remote sensing techniques offer the opportunity to monitor the wave field in larger areas at low costs and with little supervision and maintenance. Amongst those new technologies is the wave measurement by analysis of navigational X-Band radar data. X-Band radar sensors are in widespread use for ship traffic control and navigation purposes and are installed on nearly every off-shore installation and larger vessel. By adding new hardware and software components, the nautical radar can be used as wave sensor. Wave measurements by X-Band radar systems are a reliable data source for supporting offshore as well as harbour operations or ship routing services.

Figure 1: Components of X-band radar system

Measurement principle

Figure 2: Example of a radar image obtained by X-band radar system on board a vessel.
Figure 3: 2-Dimensional Frequency-Direction Spectrum obtained by X-band radar system on board a vessel.

It is known that under certain conditions signatures of the sea surface are visible in the near range (< 5 km) of nautical radar images: The local wind generates small surface ripple waves (i.e. small waves with wave length of a few cm). The rough water surface reflects a part of the incidence radar beams. Given a wind speed of more than approximately 3 m/s, the backscatter from sea surface becomes visible in radar images. This base signal is modulated by longer ocean waves ('surface gravity waves' with wave length in the order of magnitude of some 10 m to several 100 m), generating a stripe like pattern, the so-called 'sea clutter'. Typically, sailors suppress this signal because they consider it noise. However, it contains valuable information on the actual sea state: As the basic imaging mechanisms of ocean waves in radar images are known (Alpers et al, 1981[1]; Plant and Keller, 1990[2]), it is possible to analyse the spatial and temporal development of these pattern to gain information on wave height, wave length, wave period, surface current and other (see also the article Use of ground based radar in hydrography)

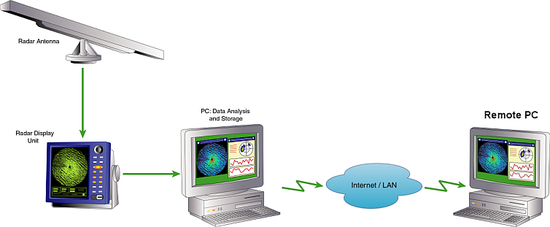
Oceanographic measurement systems based on X-band radar allow to scan the ocean surface in real time with high temporal (1 – 2 s) and spatial (5 – 10 m) resolution. A water surface of several km2 can be monitored continuously. These remote sensing systems can be installed on moving vessels as well as on fixed platforms or at coastal sites. For wave measurements, the radar raw signal is digitized and transferred to an analysis computer. Results can be displayed on site or transferred to remote locations via internet.

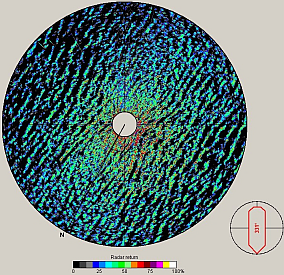
A typical wave measurement by means of X-Band radar is composed of a temporal sequence of sea clutter images [math]I(x,y,t)[/math] (see also Figure 2). To derive wave information from such data sets, several analysis steps are required.

First, the images sequence is transformed into the spectral domain by means of a discrete 3D Fourier Transform. The resulting 3D image spectrum is a function of wave number [math]\vec{k}=(k_x,k_y)[/math] and frequency [math]\omega[/math]. It can be transformed into an energy density spectrum of the ocean surface waves by correcting for distortions due to the imaging mechanism and exploiting the known dispersion relation of water waves (Young et al, 1985[3], Ziemer and Rosenthal, 1987[4]). The dispersion relation describes the temporal and spatial evolution of ocean waves in spectral domain. It is used as a filter function to separate the wave signal in the image spectra from background noise and patterns not related to the wave field. In this step, the mean encounter current speed [math]U[/math] (current component directed to the radar) and direction [math]\theta_U[/math] is determined (Seemann, 1997[5], Nieto Borge et al, 1999[6]). For a fixed platform, this corresponds to the ‘true’ current, whereas for a moving vessel ship speed and course is used to derive the true mean current from this data.

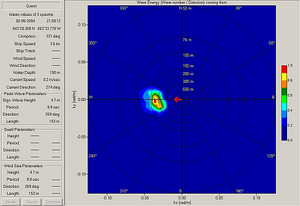
The resulting 2D ocean wave spectrum (see also Figure 3) [math]E(\omega, \theta)[/math] is usually expressed as a function of wave frequency [math]\omega[/math] and wave direction [math]\theta[/math]. It gives a comprehensive description of the sea state. Integration over all directions yields the 1D wave spectrum [math]S(\omega)[/math]. Commonly, various statistical sea state parameters are calculated from these spectra to give a compact description of the wave climate. See Statistical description of wave parameters.

Obtained sea state parameters

Figure 4: Comparative time series of significant wave height measured from X-band radar system and wave rider buoy on board 2/4k Ekofisk platform in the North Sea.
Figure 5: Comparative time series of peak wave period and peak wave direction measured from X-band radar system and wave rider buoy at the Island Helgoland in the German Bight
Figure 6: Comparative time series of peak wave length measured from X-band radar system and wave rider buoy at the Island Helgoland in the German Bight.

Significant wave height

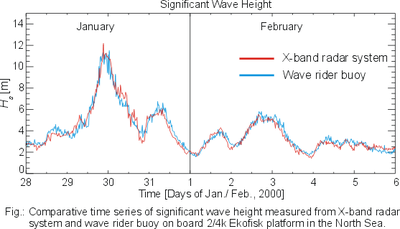
In contrast to in situ sensors, the wave spectra determined from radar images are not properly scaled. Thus, the total wave energy and the significant wave height cannot be computed directly from these spectral estimates. It has been shown that the significant wave height is linearly dependent on the square root of the signal-to-noise ratio (SNR), where the signal is assumed as the total energy of the wave spectrum estimation derived by the sea clutter analysis mentioned above and the noise is computed as the energy due to the speckle caused by the sea surface roughness (Alpers and Hasselman, 1982[7]). The significant wave height is determined by using a linear regression equation, which relates the root square of the signal-to-noise ratio of the radar images to the significant wave height (Nieto Borge et al., 1998[8]) (see also Figure 4). The correlation between significant wave heights derived from in situ data and the square root of the signal-to-noise ratio derived from radar measurements is close to 90%.

Peak wave period and direction

The peak wave period and direction can be derived from the frequency-direction spectrum [math]E(\omega, \theta)[/math] (Young et al, 1985[3] (see also Figure 5). They are defined as the location of the energy maximum within the spectrum. To determine the peak frequency, the centroid formula can be used which implies a frequency interval of 80 % energy maximum. This method is recommended by IAHR/ AIRH because of its high stability with respect to theoretical spectral variability. The wave period can also be derived by the spectral moments obtained over the full range of frequencies.

Peak wave length

Wave length and periods of ocean waves are connected by the dispersion relation. Thus, it is possible to express wave spectra as a function of frequency ([math]E(\omega, \theta)[/math]) or wave number ([math]E(k, \theta)[/math]). The peak wave length can be determined from [math]E(k, \theta)[/math] directly in the same way as the peak period (see also Figure 6).

Surface current calculation

The surface current is obtained by minimising the distance between the location of the spectral energy in the 3D image spectrum and its theoretical position defined by the dispersion relation for linear surface gravity waves. The surface current is the basic step to calculate directional wave spectra from radar images (see also currents).

Wave systems

X-Band radar systems are able to resolve multiple wave systems, e.g. swell and wind sea systems. Usually, swell is characterized by its phase speed: Swell waves propagate faster than the wind, where as wind driven waves can not travel faster than the wind that generated these waves (see also waves).

Output of X-band radar systems

Resolution and limits

The resolution of sea state measurements of X-band radar systems are limited by the properties of the radar sensor:

  • The spatial resolution is limited by the sampling frequency (SFR), antenna aperture [math]\Phi_A[/math] and the size of the analysis areas [math]N_x \times N_y[/math] placed within in the radar image.
  • The temporal resolution is limited by the antenna repetition rate (RPT) and the number [math]N_t[/math] of images used for the wave analysis.

Output parameters and accuracy

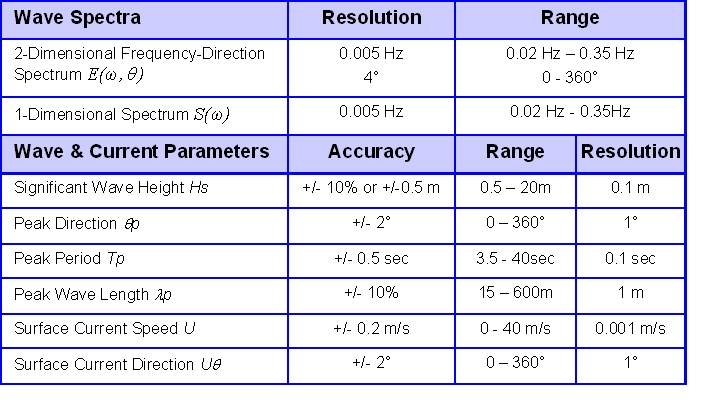
Figure 7 lists the standard output parameters with corresponding resolutions, ranges, and accuracies. These values indicate typical ranges. The numbers depend on the radar hardware, the total time of measurement and therefore can vary for each individual installation.

Figure 7: Standard output parameters of X-band radar system with corresponding resolutions, ranges, and accuracy.

See also

Internal links

External links

Examples of X-band Radar Systems:

References

  1. ↑ Alpers, W., Ross, D.B., and Rufenach, C.L. 1981. On the Detectability of Ocean Surface Waves by Real and Synthetic Aperture Radar. Journal of Geophysical Research 86: 6481-6498
  2. ↑ Plant, W.J. and Keller, W.C. 1990. Evidence of Bragg scattering in microwave Doppler spectra of sea return, J.Geophys. Res. 95(C9): 16,299-16,310
  3. ↑ 3.0 3.1 Young, I.R., Rosenthal, W. and Ziemer, F. 1985. A Three-dimensional analysis of marine radar images for the determination of ocean wave directionality and surface currents. J. Geophys. Res. 90: 1049 -1059.
  4. ↑ Ziemer F. and Rosenthal, W. 1987. On the Transfer Function of a Shipborne Radar for Imaging Ocean Waves. Proc. IGARSS'87 Symp. Ann Arbor. Michigan, May 1987, pp 1559-1564.
  5. ↑ Seemann, J. 1997. Interpretation of the Structure of the frequency-wave number spectrum of nautical radar temporal sequences of sea states (in German). Hamburg, Germany: University of Hamburg, Ph.D. thesis.
  6. ↑ Nieto Borge, J.C., Hessner, K., and Reichert, K. 1999. Estimation of the Significant Wave Height with X-Band Nautical Radars. Proceedings of the 18th OMAE Conference, St John’s, New Foundland, Canada.
  7. ↑ Alpers, W. and Hasselmann, K. 1982. Spectral signal to clutter and thermal noise properties of ocean wave imaging synthetic aperture radars. Int. J. Remote Sens. 3: 423–446
  8. ↑ Nieto Borge, J.C., Reichert, K. and Dittmer, J. 1998. Use of Nautical Radar as a Wave Monitoring Instrument. Coastal Engineering 37: 331-342
The main author of this article is Traenkmann, Ina
Please note that others may also have edited the contents of this article.
Citation: Traenkmann, Ina (2024): Waves and currents by X-band radar. Available from http://www.coastalwiki.org/wiki/Waves_and_currents_by_X-band_radar [accessed on 22-12-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Waves_and_currents_by_X-band_radar&oldid=80658"