Beach groundwater
Beach morphodynamics not only depends on water flow over the beach surface, but also on subsurface water flow. Surface flow and subsurface flow are related through infiltration and exfiltration. The groundwater table fluctuates at different timescales: the timescale of swash (wave uprush and backwash), the timescale of alternating high and low tidal waters and the seasonal time scale of storm surges and fresh water runoff.
Groundwater flow is much stronger in coarse-grained sediments (hydraulic conductivity [math]K \sim 10^{-3} m/s[/math]) than in medium/fine-grained substrates ([math]K \sim 10^{-5} m/s)[/math]. Most laboratory and field observations of groundwater flow refer to coarse-grained beaches.
The water flow through the beach surface influences the net sediment transport up or down the beach, resulting in accretion or erosion (see Swash zone dynamics). The water circulation associated with the fluctuating groundwater table influences the mixing of seawater and fresh water, with an impact on subsurface seawater intrusion (see Submarine groundwater discharge).
This article introduces some principles of beach groundwater dynamics.
Contents
Subsurface zones
In this article we consider beach soils which are homogeneous over a depth range of at least the tidal range and the swash excursion. Three zones in the beach subsurface soil can be distinguished:
- the unsaturated upper beach (also called vadose zone), where the pores (sediment grain interstices) contain air as well as water. The vadose zone extends from the top of the beach surface to the capillary fringe. Water infiltrating in the vadose zone has a pressure head less than atmospheric pressure, and is retained by a combination of adhesion and capillary action.
- the intermediate capillary fringe (tension-saturated zone), in which groundwater seeps up from the water table by capillary action, completely filling the pores. The thickness of the capillary fringe can be up to about one meter in very fine sediment and not exceed a few centimeters in very coarse sediment.
- the saturated lower beach (phreatic zone), the zone below the water table where the pressure head equals the atmospheric pressure and where grain interstices are completely filled with water. The pore space, which is a fraction of the grainsize, largely determines the hydraulic conductivity of the soil. Pore water can contain a small fraction of air which strongly influences the transmission depth of pore water pressure fluctuations (see Wave-induced soil liquefaction).
Groundwater response at the tidal time scale
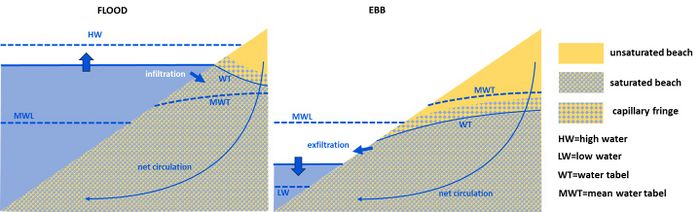
Figure 1 shows the groundwater response of a sloping beach on the tidal time scale. On this time scale, sea level can be considered as rising and falling with a nearly horizontal flat surface. The water table rises faster during high tide (rising sea level) than it falls during low tide (falling sea level). During falling tide, a seepage face is formed, where groundwater exfiltrates onto the beach.
Water infiltrates the dry beach face more easily than it drains from the sand matrix, unless the beach consists of very porous coarse material. The tidal mean water table is therefore higher than the mean sea level[2]. Most seawater infiltrates near the high tide mark and exfiltrates near the low tide mark, resulting in a net groundwater circulation from the upper to the lower tidal zone. Some characteristics of the groundwater response at the tidal timescale are explained with the simple analytical model described in the appendix.
Groundwater response at the wave time scale
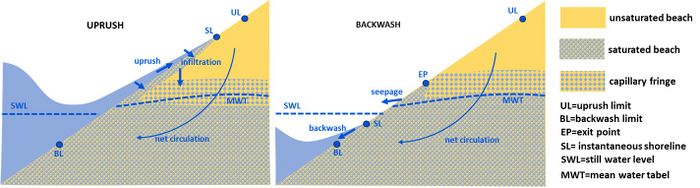
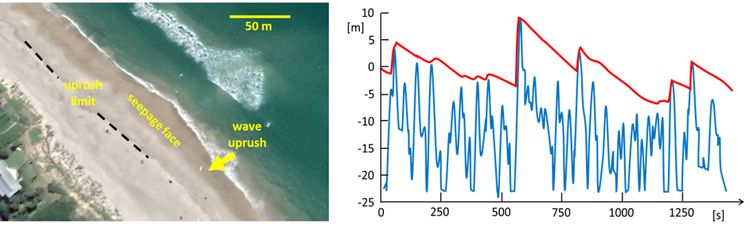
Figure 2 illustrates seawater infiltration into the unsaturated beach. Here, the water table and the capillary fringe are lagging behind the wave uprush, a situation that may occur during flood. A wetting front forms beneath the uprushing swash lens, resulting in downward infiltration through the unsaturated zone. During backwash, the water table intersects with the beach surface above the retreating backwash lens, forming a seepage face with a shiny appearance where groundwater exfiltrates (Fig. 3). The exit level (intersection of the water table with the beach surface) gradually declines and finally drops below the capillary fringe.
Similarly as with the tide, seawater infiltrates the beach more readily during the uprush stage than it drains during the backwash stage[3]. The resulting elevation of the water table is further enhanced by wave set-up. Beach sand permeability and water saturation greatly influence the water exchange rate across the beach face. In the case of a coarse sandy beach, the unsaturated zone is rapidly filled by the infiltrating seawater. In fine sediment, on the other hand, the wedge-shaped wetting front is kept close to the beach surface for most of the uprush and does not penetrate far into the saturated zone[1]. The wetting front declines during backwash, but this decline is much slower than the backwash retreat (Fig. 4).
Groundwater circulation
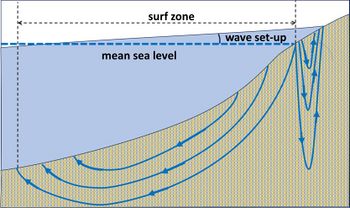
Most seawater infiltrates in the upper swash zone, while most exfiltration occurs near the backwash limit – the point where the next incoming wave collapses onto the beach. Groundwater circulation is therefore not only induced by the tide, but also by wave up- and downrush on the beach. This wave- and tide-induced groundwater circulation adds to the groundwater circulation driven by the net offshore hydraulic head gradient that is related to wave set-up in the surf zone and wave set-down in the shoaling zone[6][7] (see Wave set-up). This circulation extends from beneath the beach face down to the offshore limit of the surf zone (Fig. 5). Much of the submarine groundwater discharge is due to the circulation caused by these different mechanisms[8] and therefore consists mainly of seawater rather than inland fresh groundwater. See also Submarine groundwater discharge.
Appendix: Beach water table dynamics
This appendix reproduces a model developed by Nielsen (1990[9]) providing an analytical description of the tidal dynamics of the beach water table. This model is based on several simplifying approximations. The most important simplification consists of ignoring the seepage face; the ground water table is assumed to intersect the beach face at sea level, during both rising and falling tide. Other simplifications are: alongshore uniformity, horizontal ground water flow, uniform beach slope, uniform sediment composition.
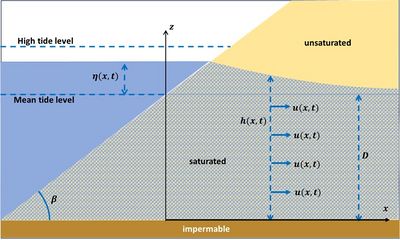
Symbols are (see also Fig. 6): [math]x=[/math] landward horizontal coordinate, [math]t=[/math] time, [math]\eta(x,t)=a \, \cos(\omega t – kx) =[/math] tide level variation, [math]\omega= 2 \pi / T =[/math] tide radial frequency, [math]k=2 \pi / L=[/math] tide wave number, [math]h(x,t)=[/math] beach groundwater table, [math]D=[/math] groundwater flow depth relative to mean tide level, [math]u(x,t)=[/math] horizontal ground water flow velocity, [math]\beta=[/math] beach slope, [math]K \, (\sim 10^{-3}-10^{-5} \,m/s)=[/math] hydraulic conductivity, [math]n \, (\sim 0.4)=[/math] beach porosity.
The groundwater flow [math]u(x,t)[/math] is given by Darcy's law, [math]\; u(x,t) = - K \, \partial h(x,t) / \partial x[/math].
The groundwater mass balance equation is [math]\; n \, \partial h(x,t) / \partial t = - \partial \big( h(x,t)u(x,t) \big) / \partial x[/math].
Elimination of [math]u[/math] from these equations gives the nonlinear diffusion equation
[math]\dfrac{\partial h}{\partial t} = \dfrac{K}{n} \dfrac{\partial}{\partial x} \Big( h\, \dfrac{\partial h}{\partial x} \Big) \, . \qquad (1)[/math]
Boundary conditions are: [math]\partial h /\partial t \rightarrow 0 \, , \; t \rightarrow \infty \; ; \quad h(x_0,t) = D + a \cos \omega t \, , \; x_0= a \cos \omega t / \tan \beta \, . \qquad (2)[/math]
These boundary conditions allow water infiltration and exfiltration through the beach face. There is no simple solution of Eqs. (1,2) because of their nonlinear nature. Due to this nonlinearity, we cannot expect the water table to follow the same sinusoidal variation as the tidal height, because the response of groundwater flow to tidal rise and fall has an asymmetric character.
An approximate solution can be obtained for small values of the parameter [math]\epsilon = k_B\, A\, \cot \beta \;[/math], where [math]k_B[/math] is the beach wavenumber [math]k_B = \sqrt{\dfrac{n \omega}{2 K D}}[/math].
Small values of [math]\epsilon[/math] only occur for very small tidal amplitude [math]a[/math] and for steep beaches consisting of very coarse material. In this case the solution to first order in [math]\epsilon[/math] is given by the expression
[math]h(x,t) = D + a \, e^{-k_B x} \cos (\omega t – k_B x) + \dfrac{\epsilon \, a }{2} \, \Big(1 + \sqrt{2} \, e^{- \sqrt{2} \, k_B x } \, \cos \big( 2 \omega t + \dfrac{\pi}{4} - \sqrt{2} \, k_B x \big) \Big) \, .[/math]
This formula is not representative for most field situations. In practice, the parameter [math]\epsilon[/math] is seldom small and during tidal fall the retreat of the exit point does not keep pace with sea level, but a substantial seepage face is formed. In spite of this, the formula reflects characteristics that are observed in the field. First, it shows that the groundwater level is on average higher (about [math]\epsilon \, a /2[/math]) than the average sea level. Second, the phase of the first order correction term is such that the rise of the groundwater level is faster than the fall; the infiltration rate when the sea level rises is greater than the exfiltration rate under sea level fall.
Related articles
- Swash
- Swash zone dynamics
- Submarine groundwater discharge
- Groundwater management in low-lying coastal zones
- Beach drainage
- Wave-induced soil liquefaction
References
- ↑ 1.0 1.1 1.2 Zheng, Y., Yang, M. and Liu, H. 2024. Coastal groundwater dynamics with a focus on wave effects. Earth-Science Reviews 256, 104869
- ↑ Turner, I.L., Coates, B.P. and Acworth, R.I. 1997. Tides, waves and the super-elevation of groundwater at the coast. J. Coast. Res. 13: 46–60
- ↑ Heiss, J.W., Ullman, W.J. and Michael, H.A. 2014. Swash zone moisture dynamics and unsaturated infiltration in two sandy beach aquifers. Estuar. Coast. Shelf Sci. 143: 20–31
- ↑ Cartwright, N., Baldock, T.E., Nielsen, P., Jeng, D-S. and Tao, L. 2006. Swash-aquifer interaction in the vicinity of the water table exit point on a sandy beach. J. Geophys. Res. 111, C09035
- ↑ Massel, S.R. 2001 Circulation of groundwater due to wave set-up on a permeable beach. Oceanologia 43: 279–290
- ↑ Longuet-Higgins, M. S. 1983. Wave set-up, percolation and undertow in the surf zone. Proc. Roy. Soc. London A390: 283–291
- ↑ Przyborska, A. 2014. Groundwater flow due to a nonlinear wave set-up on a permeable beach. Oceanologia 56: 477–496
- ↑ Li, L., Barry, D.A., Stagnitti, F. and Parlange, J-Y. 1999. Submarine groundwater discharge and associated chemical input to a coastal sea. Water Resour. Res. 35: 3253-3259
- ↑ Nielsen, P. 1990. Tidal dynamics of the water table in beaches. Water Resour. Res. 26: 2127-2134
Please note that others may also have edited the contents of this article.
|