Bedforms and roughness

Definition of Bedforms: Bedforms are relief features generated by fluid flow over a bed consisting of movable sediments. This is the common definition for Bedforms, other definitions can be discussed in the article

This article deals with small- to medium-scale bedforms (ripples and dunes) that affect hydrodynamics by generating bed roughness. Large-scale bedforms are dealt separately with in other articles: Nearshore sandbars, Rhythmic shoreline features, Sand ridges in shelf seas.

A description is given of the main types of bedforms, their characteristics and formation mechanisms and their influence on boundary layer and momentum dissipation processes. Relevant empirical formulas are provided in an Appendix.

Introduction

Fig. 1: Bed forms in steady flows (rivers). From Simons and Richardson (1966).

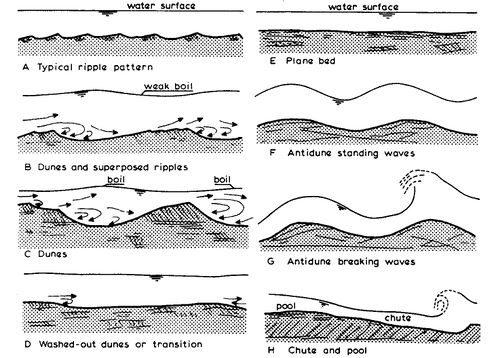
Bedforms are the dominant source of flow resistance at the local scale in sand-bed river channels and estuaries. They increase hydraulic roughness by generating flow separation and turbulent eddies, which transfer momentum from the mean flow to turbulence. This turbulent kinetic energy is ultimately dissipated as heat by viscous processes.

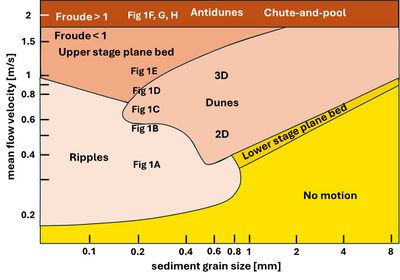
A wide variety of bedforms can develop under steady flow over a sand bed. These are commonly grouped into three transport regimes (see Figs. 1, 2):

• Lower transport regime: flat bed (no motion or weak motion), ribbons and ridges, ripples, dunes, and bars;
• Transitional regime: washed-out dunes and developing upper-stage plane bed or sand waves;
• Upper transport regime: flat mobile bed (upper-stage plane bed) and antidunes.

Bedforms whose crests are perpendicular (transverse) to the main flow direction are called transverse bedforms, such as ripples, dunes, and antidunes. Ripples typically have wavelengths much smaller than the flow depth, whereas dunes have wavelengths comparable to or larger than the flow depth. Crestlines may be straight, sinuous, linguoid, or lunate in planform. Ripples and dunes migrate downstream through erosion on the upstream face (stoss side) and deposition on the downstream face (lee side). Antidunes, in contrast, migrate upstream due to erosion on the lee side and deposition on the stoss side, reflecting their association with supercritical flow conditions. Bedforms with crests aligned parallel to the flow are called longitudinal bedforms, such as ribbons and ridges.

Various classification schemes have been proposed to describe sand-bed bedforms. These typically relate bedform type to dimensionless flow and sediment parameters, including the Froude number, sediment mobility parameter (Shields parameter), suspension parameter, and dimensionless grain size.

A flat, immobile bed occurs below the threshold of sediment motion. Just above this threshold, sediment transport begins and a flat mobile bed may exist before bedforms develop. In some cases, the bed surface may also exhibit relict bedforms formed during earlier periods of stronger flow.

The seabed boundary layer

Steady currents

In a very thin layer above the seabed, currents dissipate horizontal momentum [math]\rho \, u[/math] through viscous stresses ([math]\rho=[/math] density, [math]u=[/math] horizontal current velocity). The viscosity [math]\nu[/math] represents the diffusion process through which momentum is ultimately dissipated into heat. Momentum dissipation near the bed induces strong velocity shear [math]du/dz[/math] that destabilizes the current above the thin viscous layer, thus generating eddy-type turbulent velocity fluctuations. Close to the seabed, turbulent eddies are small, but their size increases with distance [math]z[/math] from the bed. The effect of turbulence on momentum transfer can be represented using an apparent viscosity, called the eddy viscosity, denoted here by the diffusion coefficient [math]N[/math]. The vertical momentum flux is the shear stress generally represented by the symbol [math]\tau[/math]. In steady, uniform flow, the stress in the boundary layer is approximately constant, [math]\tau = \tau_c \; [/math] (independent of depth - otherwise, the flow would accelerate or decelerate). The turbulent momentum flux is modeled using a diffusion law, [math]\tau_c =\rho \, N \, du/dz[/math]. Very close to the bed (typically within a viscous sublayer less than about 1 mm thick), molecular viscosity dominates and the effective viscosity is approximately uniform. The velocity therefore increases linearly with height in this layer.

Above the viscous sublayer lies the logarithmic boundary layer, where momentum transfer is mainly due to turbulence. Here, the eddy viscosity increases approximately linearly with the size of turbulent eddies, [math]N= \kappa u_{c*} z[/math], where [math]\kappa \approx 0.4[/math] is the so-called Karman constant and [math]u_*[/math] the so-called friction velocity. The friction velocity is defined by [math]u_{c*} = \sqrt{\tau_c / \rho}[/math]. The ratio of friction velocity and depth-averaged flow velocity [math]U_c[/math] is usually assumed constant, represented by the square root of the drag coefficient [math]c_D[/math], i.e. [math]\; u_{c*} / U_c = \sqrt{c_D}[/math]. Because the stress [math]\tau_c[/math] is constant, the velocity gradient is inversely proportional to [math]z[/math], meaning that the velocity has a logarithmic profile, [math]u(z)=\dfrac{u_{c*}}{\kappa}\ln \dfrac{z}{z_0}[/math]. Here, [math]z_0[/math] is the hydrodynamic roughness length, related to the average height [math]k_s[/math] of roughness elements on the seabed (the spacing and steepness of the roughness elements are also relevant). For a flat sandy seabed, [math]z_0[/math] is commonly assumed to be about 30 times the median grainsize [math]d_{50}[/math]. The linear increase of the eddy diffusion coefficient with [math]z[/math] holds only in the so-called logarithmic boundary layer, which is usually a few meters up to about 5 meters deep in energetic coastal flows, depending on water depth, stratification, and turbulence intensity. Above this region, turbulence still transfers momentum, but the velocity profile generally deviates from a simple logarithmic form.

Wave boundary layer

The above discussion applies to steady currents. In contrast, wave orbital motion is oscillatory, reversing direction every few seconds. Because of this rapid reversal, large turbulent eddies do not have sufficient time to develop fully. As a result, eddy diffusivity is confined to a relatively thin region near the bed, called the wave boundary layer with thickness [math]h_w[/math]. Within this layer, a logarithmic velocity profile often exists instantaneously near the bed. However, outside the thin wave boundary layer, the orbital velocity amplitude [math]U_w[/math] is largely unaffected by bed friction (see Shallow-water wave theory). This produces large velocity gradients and correspondingly high bed shear stresses. The friction velocity associated with waves is [math]u_{w*} = \sqrt{\tau_w / \rho}[/math] and the wave friction factor is defined as [math]f_w = 2 u_{w*}^2/U_w^2[/math]. Because shear is concentrated in a thinner layer, the wave friction factor [math]f_w[/math] is typically larger than the steady-current drag coefficient [math]c_D[/math].

Turbulence closure and empirical formulas

There are no analytical process-based expressions for the turbulent momentum fluxes in either steady currents or oscillatory wave motion, because turbulence is inherently chaotic. Instead, eddy viscosity models and friction formulas are based on semi-empirical theory and calibrated using laboratory experiments, field measurements, and numerical simulations. Widely used formulations are provided in the Appendix.

Bed roughness

Nikuradse introduced the concept of an equivalent sand roughness height, [math]k_s[/math], to represent the hydraulic resistance of arbitrary rough surfaces in turbulent flow. This parameter allows complex natural bed roughness to be modeled using an equivalent uniform sand grain roughness. For movable sediment beds, the effective roughness height [math]k_s[/math] consists of two main components:

• Grain roughness ([math]k'_s[/math]), associated with skin friction acting directly on sediment grains;
• Form roughness ([math]k''_s[/math]) associated with pressure drag caused by flow separation over bedforms such as ripples and dunes.

Correspondingly, the total bed shear stress ([math]\tau[/math]) can be partitioned into:

• Skin-friction shear stress ([math]\tau'[/math]), acting on the grains and responsible for sediment transport;
• Form-drag shear stress, ([math]\tau''[/math]), caused by pressure forces on bedforms.

The effective roughness height is not constant for a given sediment size but depends strongly on flow conditions, because bedforms evolve with flow strength. Field data from the Mississippi River, for example, show that [math]k_s[/math] may decrease from values on the order of 0.5 m at low flow velocities (≈ 0.5 m/s), when large dunes are present, to about 0.001 m at higher velocities (≈ 2 m/s), when bedforms become flattened or are washed out and grain roughness dominates.

The distinction between skin-friction shear stress and form-drag shear stress is important because they affect sediment transport in different ways. Skin-friction shear stress determines how much sediment is lifted from the seabed and transported by the flow, either as bedload or suspended load (see Sediment transport formulas for the coastal environment). Form-drag shear stress influences sediment transport indirectly by affecting the current velocity and, consequently, the skin-friction shear stress.

A fundamental challenge in predicting bed roughness is the mutual dependence between flow and bed morphology. Bedform dimensions—and thus hydraulic roughness—depend on flow depth, velocity, and sediment transport rate. At the same time, these flow variables depend on bed roughness through flow resistance. This feedback makes roughness prediction inherently coupled and nonlinear.

A second complication is the unsteady nature of natural flows. During rising and falling discharge, bedforms continuously adjust to changing hydraulic conditions. Because bedform dimensions respond with a finite time lag, bed roughness and friction coefficients are often in a transient, nonequilibrium state.

A third factor affecting bed roughness is biological activity. Microorganisms can stabilize the bed by binding sediment particles and forming biofilms or extracellular polymeric substances (EPS), which reduce sediment mobility and bed friction. Conversely, bioturbating organisms can destabilize the bed and increase roughness. Aquatic vegetation such as seagrass and macroalgae may either increase total flow resistance through vegetation drag or reduce sediment mobility by stabilizing the bed. These biotic influences are discussed further in Biogeomorphology of coastal systems.

Bedforms in steady and oscillating flow

Many of the processes that generate bedforms in steady flow also generate bedforms in oscillatory flows. This holds for dunes and bars which have similar characteristics in rivers and estuaries. Bed ripples are an ubiquitous feature in rivers as well as in coastal environments. However, wave-generated ripples have specific characteristics and are therefore discussed in more detail in two separate articles, Wave ripples and Wave ripple formation. Empirical formulas of bedform characteristics, bed roughness and friction are provided in the Appendix. Formulas typical for estuaries are given in the article Bed roughness and friction factors in estuaries.

Current-generated ripples

Fig. 2. Bedform stability diagram for unidirectional currents. Redrawn after Southard and Boguchwal (1990)

Small-scale ribbon and ridge type bed forms parallel to the main flow direction have been observed in laboratory flumes and small natural channels, especially in case of fine sediments (grainsize [math]d_{50}[/math] typically smaller than 0.1 mm). They are probably generated by secondary flow phenomena and near-bed turbulence effects (burst-sweep cycle) in the lower and transitional flow regime. These bed forms are also known as parting lineations because of the streamwise ridges and hollows with a vertical scale equal to about 10 grain diameters. These bed forms are mostly found in fine sediments ([math]0.05 \lt d_{50} \lt 0.25 \; mm[/math]).

When the velocities are somewhat larger (10%-20%) than the critical velocity for initiation of motion and the median particle size is smaller than about 0.5 mm, small (mini) ripples are generated at the bed surface. Ripples that are developed during this stage remain small with crest perpendicular (transverse) to the main flow direction and a ripple length much smaller than the water depth (Fig. 1A). The characteristics of mini ripples are commonly assumed to be related to the turbulence characteristics near the bed (burst-sweep cycle).

Fig. 3. Current-generated linguoid ripples, Kennetcook River, Nova Scotia, Canada. Photo credit J. Waldron https://sites.ualberta.ca/~jwaldron/

Current ripples have an asymmetric profile with a relatively steep downstream face (lee-side) and a relatively gentle upstream face (stoss-side). As the velocities near the bed become larger, the ripples become more irregular in shape, height and spacing yielding strongly three-dimensional ripples. In this case the variance of the ripple length and height becomes rather large. These ripples are known as lunate ripples when the ripple front has a concave shape in the current direction (crest is moving slower than wing tips) and are called linguoid ripples when the ripple front has a convex shape (crest is moving faster than wing tips, Fig. 3). The largest ripples may have a length up to the water depth and are commonly called mega-ripples.

Dunes

Another typical bed form type of the lower regime is the dune-type bed form (Figs. 1B, 1C). Dunes have an asymmetrical (triangular) profile with a rather steep lee-side and a gentle stoss-side. A general feature of dune type bed forms is lee-side flow separation resulting in strong eddy motions downstream of the dune crest. The length of the dunes is strongly related to the water depth ([math]h[/math]) with values in the range of [math](3 - 15) \, h[/math], with [math](6 - 7) \, h[/math] as most usual value. Extremely large dunes with heights ([math]\Delta[/math]) of the order of 7 m and lengths ([math]\lambda[/math]) of the order of 500 m have been observed in the Rio Parana River (Argentina) at water depths of about 25 m, velocities of about 2 m/s and bed material sizes of about 0.3 mm. In shallow flows, high-angle dunes develop that are asymmetric with an upstream (stoss) slope averaging 2–6 degrees and a maximum leeside slip face slope > 24 degrees. The lee slopes are controlled by granular avalanches (sediment flows dominated by grain-grain collisions). In deeper rivers, low-angle dunes develop that are more symmetrical and have slip face slope < 24 degrees, i.e. less than the theoretical limit for granular avalanches dominated by grain-to-grain contacts.

Sand bars

The largest bed forms in the lower regime are sand bars (such as alternate bars, side bars, point bars, braid bars and transverse bars), which usually are generated in areas with relatively large transverse flow components (bends, confluences, expansions). Alternate bars are features with their crests near alternate river bends. Braid bars actually are alluvial "islands" which separate the anabranches of braided streams. Numerous bars can be observed distributed over the cross-sections. These bars have a marked streamwise elongation.

Transitional regime

It is a well-known phenomenon that the bed forms generated at low velocities are washed out at high velocities (Figs. 1D, 1E). It is not clear, however, whether the disappearance of the bed forms is accomplished by a decrease of the bed form height, by an increase of the bed form length or both. Flume experiments with sediment material of about 0.45 mm show that the transition from the lower to the upper regime is effectuated by an increase of the bed form length and a simultaneous decrease of the bed form height. Ultimately, relatively long and smooth sand waves with a roughness equal to the grain roughness are generated .

In the transition regime the sediment particles will be transported mainly in suspension. This will have a strong effect on the bed form shape. The bed forms will become more symmetrical with relatively gentle lee-side slopes. Flow separation will occur less frequently and the effective bed roughness will approach to that of a plane bed. Large-scale bed forms with a relative height ([math]\Delta / h[/math]) of 0.1 to 0.2 and a relative length ([math]\lambda / h[/math]) of 5 to 15 were present in the Mississippi river at high velocities in the upper regime.

Antidunes

Fig. 4. Antidunes in the Willamette River (USA). Photo credit Marli Miller https://geologypics.com/

In the supercritical upper regime the bed form types will be plane bed and/or anti-dunes. The latter type of bed forms are sand waves with a nearly symmetrical shape in phase with the water surface waves (Fig. 1F, Fig .4). Due to the supercritical flow regime the water surface elevation mimics the bed elevation. Antidunes are bed forms with a length scale of less than 10 times the water depth. They move upstream due to strong lee-side erosion and stoss-side deposition. Antidune bedforms evolve rapidly, growing in amplitude as they migrate upstream and collapse when the resultant wave at the water's surface breaks (Fig. 1G). Trains of anti-dunes waves are highly unstable, following a quasi-stochastic process of formation and destruction. When the flow velocity further increases, finally a stage with chute and pools may be generated (Fig. 1H).

Wave-generated bedforms

Fig. 5. Symmetrical ripples in biogenic, aragonitic sand (shallow subtidal seafloor just offshore from Sand Dollar Beach, new San Salvador Island, eastern Bahamas). Photo credit James St. John Creative Commons Licence.

Bedforms generated by waves are generally smaller than those produced by steady currents, because oscillatory flow limits their growth. Bagnold and Taylor (1946) distinguished two main types of wave-generated ripples: rolling-grain ripples and vortex ripples. Rolling-grain ripples form when the wave-induced bed shear stress is only slightly above the critical threshold for sediment motion. Their height is typically only a few grain diameters, and their steepness is small. Sediment transport occurs mainly as rolling and sliding of grains, with little flow separation. As the wave orbital velocity amplitude or wave period increases, ripples grow in height and wavelength. Once the ripple steepness becomes sufficiently large, flow separation occurs on the lee side and coherent vortices develop. These bedforms are called vortex ripples. Vortex ripples are commonly classified into three regimes—orbital, suborbital, and anorbital—depending on the ratio between wave orbital excursion and ripple dimensions (see Wave ripples).

Orbital bedforms typically form when the wave period [math]T[/math] is small. Their wavelength scales with the near-bed orbital excursion, [math]\lambda_r = (1.3-1.4) \, a [/math], where [math]a[/math] is the horizontal orbital excursion amplitude.

Suborbital ripples form when the orbital excursion becomes large relative to ripple dimensions. In this regime, ripple wavelength becomes less dependent on orbital excursion and may decrease with further increases in orbital diameter, reflecting a transition toward grain-size-controlled bedforms.

Anorbital bedforms typically occur for large wave orbital excursions [math]a \gt 10^3 \, d_{50}[/math]. Their wavelength is proportional to the mean grain size [math]d_{50}[/math], [math]\quad \lambda_r \approx (400-600) \; d_{50} [/math] and the ripple height [math]\eta_r[/math] is small, on the order of [math]\eta_r \approx (0.1-0.12) \; \lambda_r[/math].

Flow separation and vortex formation occur when ripple steepness, [math]\eta_r / \lambda_r[/math] is sufficiently large (greater than about 0.1). Vortex dynamics play a key role in sediment transport and energy dissipation over vortex ripples. During each half-wave cycle, a vortex forms on the lee side of the ripple and grows in strength as the free-stream velocity increases. During flow deceleration, the vortex lifts away from the bed and moves toward the crest. At flow reversal, the vortex is ejected and transported over the crest toward the opposite flank, where it dissipates. This process enhances turbulent mixing and suspends sediment into the water column. Laboratory experiments by van der Werf et al. (2007) showed that ripple geometry, vortex formation, and ripple migration depend strongly on the skewness and asymmetry of the oscillatory flow. Velocity skewness refers to unequal peak velocities in opposite flow directions, while acceleration asymmetry refers to differences in acceleration during flow reversal. These properties influence boundary layer structure, sediment transport rates, ripple geometry, and migration direction, and therefore play an important role in shaping the shoreface profile of sandy coasts. See also Wave ripple formation.

Formation of bedforms

Fig. 6. Schematic representation of bedform formation. Top: Steady flow from left to right. The bed-load sediment flux is maximum on the upstream side of the bedform before reaching the crest. Two successive stages of bed perturbation development are brown and yellow, respectively. The dark-blue dotted line is a near-bed streamline. The dark-blue arrows are flow vectors. Middle: Steady flow from right to left. Under: Bedform formation in oscillating flow as linear superposition of the two steady flow situations.

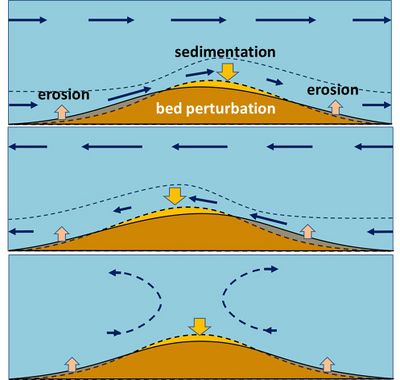
The formation of bedforms is related to the inherent instability of an initially flat sediment bed. This instability can be understood qualitatively as follows. A small perturbation of the bed modifies the flow pattern, creating zones of sediment transport convergence and divergence. The perturbation grows if sediment transport converges at the crest, causing net deposition.

This mechanism results from two interacting effects. First, streamlines are compressed on the upstream side of the perturbation, causing flow acceleration (an inertial effect). Second, the perturbation increases turbulent shear stress and momentum dissipation near the bed. Because turbulence and friction act over a limited vertical distance, the flow response differs between regions close to and far from the bed.

As flow approaches the perturbation, velocity initially increases along the upstream slope. Near the bed, however, the increasing shear stress and turbulence reduce the flow velocity near the crest. This local deceleration decreases the sediment transport capacity near the bed, promoting deposition at or near the crest. If most sediment transport occurs as bedload close to the bed, this deposition reinforces and amplifies the initial perturbation. This positive feedback mechanism explains the spontaneous growth of bedforms. The process is illustrated schematically in Fig. 6 for both unidirectional and oscillatory flow. A more detailed explanation is given in the article Principles of spontaneous bedform generation.

Different types of bedforms can develop through this instability, depending on how perturbations interact with turbulent flow structure and sediment transport under steady currents, tidal flow, or wave-driven oscillatory flow. The perturbations with the highest growth rates become dominant. Small-scale perturbations tend to generate stronger turbulence and therefore grow faster initially. However, small bedforms are also steeper and more prone to avalanching, which limits their growth. As a result, the fastest-growing and most stable bedforms typically have intermediate length scales.

These preferred length scales can be predicted using linear stability analysis, which determines the perturbation wavelength with the highest growth rate. Such analyses successfully explain the formation of most bedforms observed in sandy coastal and fluvial environments, including ripples, dunes, and larger-scale features. See also Stability models, Wave ripple formation, Rhythmic shoreline features, and Sand ridges in shelf seas.

Field observations show that dunes often develop from an initial ripple field through a nonlinear process of pattern coarsening, involving successive merging and growth of ripples. Stable bedforms with wavelengths intermediate between ripples and dunes are generally not observed. This is because smoother intermediate-scale bedforms generate weaker turbulence, which shifts the location of maximum sediment transport from upstream of the crest to downstream. This shift causes erosion of the crest and decay of the bedform. However, if such bedforms become covered with smaller ripples, the increased roughness enhances turbulence and restores upstream transport convergence, allowing further growth into fully developed dunes.

Related articles

Bed roughness and friction factors in estuaries

Wave ripples

Stability models

Wave ripple formation

Rhythmic shoreline features

Sand ridges in shelf seas

Biogeomorphology of coastal systems

Appendix Empirical estimates of bedform characteristics and associated bed roughness

Several formulas have been derived from laboratory and field experiments for estimating bedform characteristics (especially height and wavelength). Bedforms influence currents and waves by enhancing shear stresses and associated frictional momentum dissipation in the turbulent boundary layer. Conversely, currents and waves are themselves the primary agents responsible for the emergence and development of these bedforms by inducing sediment transport. Spatial patterns in sediment transport are both cause of and caused by the development of bedforms due to the inherent instability of the flat sediment bed. Bedform characteristics depend on flow properties and flow properties depend on bedform characteristics. The empirical formulas presented in this appendix establish relationships between flow properties and bedform characteristics.

The case of currents only

Roughness and friction

Steady or low-periodic water motions in shallow coastal waters are turbulent over the whole water column. The seabed is subjected to a shear stress [math]\tau_c[/math] which is related to the depth-averaged current velocity [math]U_c[/math] through the friction coefficient [math]c_D[/math]:

[math]c_D = \Large\frac{\tau_c}{\rho U_c^2}\normalsize ,[/math]

where [math]\rho[/math] is the density of water. Sometimes other friction factors are used, such as the Chezy coefficient, the Darcy-Weisbach friction factor or the Manning coefficient, see Bed roughness and friction factors in estuaries. The friction coefficient [math]c_D[/math] is related to the thickness [math]k_s[/math] of the near-bed roughness layer (the Nikuradse length) ,

[math]k_s = 12 h \exp(\large\frac{0.4}{\sqrt{c_D}}\normalsize) , [/math] or [math]c_D=0.16 \, \Big[ \ln\Big(\dfrac{12 h}{k_s}\Big) \Big]^{-2} \approx \Big[\dfrac{0.4}{\ln(h/z_0)-1} \Big]^2[/math] ,

where [math]h[/math] is the total water depth in shallow water.

For a flat sediment bed [math]k_s \approx (2-3) \, d_{50} ,[/math] where [math]d_{50}[/math] is the median sediment grainsize.

The roughness height [math]k_s[/math] according to van Rijn (2007) can be estimated from

[math]k_s = d_{50} \, \big[85 – 65 \, \tanh(0.015(\Psi-150)) \big] ,[/math]

where [math]\Psi = \Large\frac{U_c^2}{g (s-1)d_{50}}\normalsize[/math] is the mobility parameter.

Ripple height and wavelength

Several empirical formulas have been established for the mean ripple height and ripple wavelength from field and laboratory experiments. These formulas involve the following variables:

• [math]d_* = d_{50} \, \big( \large\frac{g (s-1)}{\nu^2}\normalsize \big)^{1/3} \approx 25,000 \, d_{50}[/math] is the dimensionless mean grainsize ([math]d_{50}[/math] in meters)
• [math]s = \rho_{sediment}/\rho \approx 2.65[/math] is the effective sediment density
• [math]\nu \approx 10^{-6} m^2/s[/math] is the kinematic viscosity of water
• [math]\Theta = \Large\frac{\tau_{b}}{g \rho (s-1) d_{50}}\normalsize[/math] is the Shields parameter
• [math]\Theta_{cr} \approx 0.05 [/math] is the critical value of the Shields parameter for the onset of particle motion
• [math]\tau_c = \rho u_{c*}^2[/math] is the bed shear stress
• [math]u_{c*} = \sqrt{c_D} U_c[/math] is the friction velocity

A few popular empirical formulas for the mean ripple height and wavelength are indicated in the table below.

Reference	Data	Ripple height	Ripple wavelength
Soulsby et al. (2012)	Fully developed field of bottom ripples with flow-perpendicular straight crestlines the ripple height	[math]\eta_r = 202 \, d_{50} \, d_*^{-0.554}[/math]	[math]\lambda_r = d_{50} \, (500 + 1881 \, d_*^{-1.5}) [/math]
Flemming (1988)	Field observations in rivers and estuaries	[math]\eta_r = 0.677 \; \lambda_r^{0.809} [/math]
Lapotre et al. (2017)	Field data and dimensional analysis		[math] \lambda_r = 2504 \, d_{50}^{1/3} \Theta^{1/6} (\nu/u_*)^{2/3} [/math]
Venditti and Bradley (2022)	Field observations of river dunes	[math]\log_{10}(\Large\frac{\eta_r}{h}\normalsize) = - 0.397\, \big[ \log_{10}(\Large\frac{\Theta}{\Theta_{cr}}\normalsize) -1.14 \big]^2 - 0.503 [/math]	[math] \log_{10}(\Large\frac{\lambda_r}{h}\normalsize) = 0.098\, \big[ \log_{10}(\Large\frac{\Theta}{\Theta_{cr}}\normalsize) - 1.09 \big]^2 + 0.791[/math]

The case of waves only

A more detailed discussion of wave ripples is given in the article Wave ripples and Wave ripple formation.

Roughness and friction

The frequent reversal of the wave orbital motion along the seabed hampers the development of the turbulent boundary layer. The height of the wave boundary layer [math]h_w[/math] is generally small, of the order of one to ten centimeters. It depends on the wave phase and is largest shortly before reversal of the orbital motion. For a rough sediment bed, the height of the wave boundary layer depends primarily on the height [math]k_s[/math] of the roughness elements, the median sediment grainsize [math]d_{50}[/math] and the horizontal wave orbital excursion [math]2a[/math]. The wave orbital excursion is related to the maximum wave orbital velocity [math]U_w[/math] at the top of the wave boundary layer, [math]a= U_w / \omega [/math], where [math]\omega=2 \pi / T[/math] is the wave angular frequency and [math]T[/math] the wave period. For a rippled seabed, the wave boundary layer also depends on the ripple characteristics (height [math]\eta_r[/math] and wavelength [math]\lambda_r[/math]).

The following empirical order-of-magnitude estimates have been derived based on laboratory and field experiments:

• For viscous flow over a smooth flat sediment bed, the height of the wave boundary layer [math]h_w \approx \sqrt {\nu T /\pi }[/math]
• For turbulent flow over a smooth flat bed [math]k_s \approx (2-3) \, d_{50}[/math] and [math]\; h_w \approx 0.09 \, a^{0.82} \, k_s^{0.18}[/math] or [math]\; h_w \approx 0.28 \, a^{0.74} \, k_s^{0.26}[/math] or [math]\; h_w \approx 0.09 \, a^{0.5} \, k_s^{0.5}[/math]
• For flow over a rough bed with roughness elements of height [math]k_s[/math], [math]\quad h_w \approx 0.19 \, a^{0.81} \, k_s^{0.19}[/math]
• For a stone-covered bed [math]\; h_w \approx 0.08 \, k_s \big[ 1 + (\large\frac{a}{k_s}\normalsize)^{0.82} \big] [/math]
• For a rippled bed [math]\; k_s \approx 8 \Large\frac{\eta_r^2}{\lambda_r}\normalsize + 170 \, d_{50} \sqrt{\Theta - \Theta_{cr}}[/math]

The symbols are defined as follows:

• [math]\Theta = \Large\frac{\tau_w}{g \rho (s-1) d_{50}}\normalsize[/math] is the Shields parameter
• [math]\Theta_{cr} \approx 0.165\, (R_f+0.6)^{-0.8} + 0.045 \, \exp[-40 R_f^{-1.3}] [/math] is the critical value of the Shields parameter for the onset of particle motion
• [math]\tau_w = \rho \, u_{w*}^2[/math] is the maximum wave-induced shear stress
• [math]Re_w = \dfrac{a U_c}{\nu}[/math] is the wave Reynolds number
• [math]R_f= \dfrac{d_{50} u_{*w}}{\nu} = \sqrt{\large\frac{f_w}{2}}\large\frac{d_{50} U_w}{\nu}\normalsize[/math] is the grain Reynolds number

Order-of-magnitude estimates are [math]\Theta_{cr} \approx 0.05 , \; k_s \approx 25 \Large\frac{\eta_r^2}{\lambda_r}\normalsize [/math].

The wave friction coefficient is defined as [math]f_w = \Large\frac{2 \, \tau_w}{\rho U_w^2}\normalsize = \dfrac{2 u_{w*}^2}{U_w^2} \, .[/math]

Several empirical formulas have been established for the wave friction coefficient. Most of the formulas, valid for [math]a\gt 1.6 k_s[/math], are of the form [math]f_w = c_1 \, \exp\big[c_2 \, (\large\frac{a}{k_s}\normalsize)^{c_3} \big] [/math] with the following values: ([math]c_1 = 0.00251, c_2 = 4.57, c_3 = -0.19[/math]) , ([math]c_1=0.00123, c_2 = 5.5, c_3 = -0.16[/math]) , ([math]c_1 = 0.00184, c_2 = 5.5, c_3 = -0.2[/math]), ([math]c_1 = 0.00058, c_2 = 5.7, c_3 = -0.1[/math]).

For smooth sediment beds the friction coefficient is related to the Reynolds number [math]Re=\Large\frac{a U_w}{\nu}\normalsize[/math] : [math]f_w \approx 2 \; Re^{- 0.5} [/math] in case of laminar flow and for turbulent flow [math]f_w \approx 0.035 \, Re^{-0.16}[/math]. Soulsby and Clarke (2005) recommend [math]\; f_w \approx 0.052 \, Re^{-0.19}[/math] for smooth turbulent beds and [math]\; f_w \approx 0.24 \, (a/k_s)^{-0.52}[/math] for rough beds.

For beds covered with very large roughness elements, Dixen et al. (2008) propose [math]\; f_w \approx 0.32 \, (a/k_s)^{-0.8}[/math] if [math]a/k_s \sim O[1][/math]. For the case [math]a \gt \gt k_s[/math], Fredsoe and Deigaard (1992) propose [math]\; f_w \approx 0.04 \, (a/k_s)^{- 0.25}[/math].

Ripple height and wavelength

A large number of field and laboratory studies have been dedicated to determining the height and wavelength of seabed ripples generated by wave action. Empirical formulas for the ripple height and wavelength (orbital ripples) of a fully developed field are indicated in the table below. More empirical formulas are presented in the review article by Nelson et al. (2013). Key variables appearing in these formulas are the wave orbital excursion amplitude [math]a[/math] and the sediment mobility parameter [math]\Psi = \Large\frac{U_w^2}{g (s-1) d_{50}}\normalsize[/math].

Reference	Ripple height	Ripple wavelength
Nielsen (1981), O'Donoghue et al. (2006)	[math]\eta_r = a \, \Big(0.275 - 0.022 \, \Psi^{0.5}\Big)[/math]	[math] \lambda_r = a\, \Big(1.97 - 0.44 \, \Psi^{0.21}\Big)[/math]
Soulsby and Whitehouse (2005)	[math] \eta_r = 0.15 \, \lambda_r \Big(1-\exp(-(5000 \large\frac{d_{50}}{a}\normalsize)^{3.5}) \Big) [/math]	[math] \lambda_r = a \, \Big(1+0.00187 \large\frac{a}{d_{50}}\normalsize \big[1-\exp(-(5000 \large\frac{d_{50}}{a}\normalsize\Big)^{-1.5}) \big] \Big)^{-1} [/math]
Goldstein et al. (2013)	[math] \eta_r = 313 \, d_{50} \, \lambda_r [/math]	[math] \lambda_r = 2a \, \Big(1.12 + 2180 \, d_{50}\Big)^{-1} [/math]
Ruessink et al. (2015) for [math]d_{50}\gt 0.3 mm[/math]	[math] \eta_r = 0.164 \, \lambda_r \Big(1-\tanh(0.63 \Theta)\Big) [/math]	[math] \lambda_r = 0.676 \, a \, \Theta^{-0.163} \quad[/math]
Grasmeijer and Kleinhans (2004)	[math]\eta_r = 2 a \Psi^{-1}[/math]	[math]\lambda_r = \eta_r \, \Big(-0.078 + 0.355 \Psi^{-0.221} \Big)^{-1}[/math]
van Rijn (2007)	[math]\eta_r = a \Big( 2.8 \; 10^{-13} \, (250 - \Psi)^5 \Big)[/math]	[math]\lambda_r = 5 \; 10^6 \eta_r \, (250 - \Psi)^{-2.5}[/math]
Chen et al. (2023)	[math]\eta_r = a \, \Big(-0.2 + 0.6 \, \Psi^{-0.2} \Big)[/math]	[math]\lambda_r = \eta_r \, \Big(0.1 - 3.9 \; 10^{-4} \, \Psi \Big)^{-1}[/math]
thumb rule orbital ripples	[math]\eta_r \approx 0.1 \, \lambda_r[/math]	[math]\lambda_r \approx 1.35 \, a[/math]

Fig. 7. Empirical formulas for the prediction of ripple dimensions as a function of the mean grainsize [math]d_{50}[/math]. The wave orbital excursion [math]2a = 0.6 \, m[/math] and the near-bed wave orbital velocity [math]U_c = 0.4 \, m/s[/math]. Left: Predictions of the ripple height. Right: Predictions of the ripple wavelength.

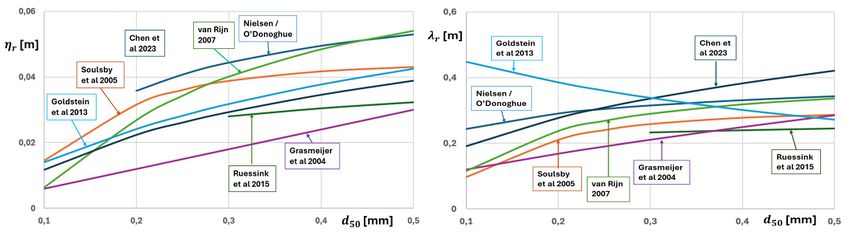
The predictions of the empirical formulas span a wide range (Fig. 7). This wide range partly reflects the strong scatter in the experimental data on which the formulas are based. However, it also suggests that ripple dimensions do not only depend on the wave orbital excursion [math]2a[/math], the sediment mobility parameter [math]\Psi[/math] and the mean grainsize [math]d_{50}[/math]. Other possibly relevant variables proposed in the literature include the wave period [math]T[/math], the Shields parameter [math]\Theta[/math], the grain Reynolds number [math]R_f[/math] and the sediment fall velocity [math]w_s[/math].

Waves and current

Results from theoretical models and laboratory and field experiments show that the presence of waves increases significantly the bottom roughness parameter for the current boundary layer, i.e., the roughness parameter depends strongly on the sea state. In contrast, it has been found that the current has little effect on the wave boundary layer..

Soulsby et al. (1993) proposed a simple empirical formula for the bed shear stress [math]\tau_{cw}[/math] of the combined effect of waves superimposed in a current, dependent on the bed shear stresses for current alone, [math]\tau_c[/math], and waves alone, [math]\tau_w[/math]. The bed shear stress averaged over the wave period, [math]\langle \tau_{cw} \rangle[/math], and the maximum bed shear stress, [math]\tau_{cw}^{max}[/math] are given by, respectively,

[math]\langle \tau_{cw} \rangle = \tau_c \, \Big[1 + 1.2 \, \Big(\dfrac{\tau_w}{\tau_c+\tau_w} \Big)^{3.2} \Big] \, , \quad \tau_{cw}^{max} = \Big[ \Big( \langle \tau_{cw} \rangle + \tau_w |\cos \phi | \Big)^2 + \tau_w^2 \sin^2 \phi \Big]^{1/2} \, . [/math]

More elaborate semi-empirical formulas were developed later by Soulsby and Clarke (2005):

[math]\langle \tau_{cw} \rangle = \dfrac{\big(\tau_c^2+\tau_w^2 \big)^{1/2}}{2 \ln (h_w/z_0)} \Bigg[ \Bigg(\dfrac{\big(\ln(h/h_w)-1 \big)^2}{2 \ln(h_w/z_0)} + 0.8 \sqrt{\rho} U_c \big(\tau_c^2+\tau_w^2 \big)^{-1/4} \Bigg)^{1/2} - \dfrac{\ln(h/h_w)-1}{\sqrt{2 \ln(h_w/z_0)}}\Bigg]^2 \, . [/math]

[math]\tau_{cw}^{max} = \Big[\Big(\langle \tau_{cw} \rangle + |\cos \phi| \tau_w^{1/2} \big(\tau_c^2+\tau_w^2 \big)^{1/4} \Big)^2 + \sin^2 \phi \, \tau_w \big(\tau_c^2+\tau_w^2 \big)^{1/2} \Big]^{1/2} \, , [/math]

where [math]\phi [/math] is the angle between the current and the wave propagation direction.

References

The main authors of this article are Leo van Rijn and Job Dronkers Please note that others may also have edited the contents of this article. Citation: Leo van Rijn; Job Dronkers; (2026): Bedforms and roughness. Available from http://www.coastalwiki.org/wiki/Bedforms_and_roughness [accessed on 5-03-2026] For other articles by this author see Category:Articles by Leo van Rijn For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Leo van Rijn For an overview of contributions by this author see Special:Contributions/Dronkers J