Embayed beaches

Fig. 1. The rocky shore of western Galicia (Spain) with numerous embayed beaches. Google Earth image.

Introduction

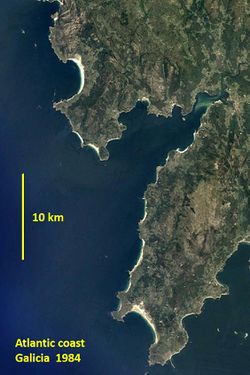
Many rocky coasts host beaches that are semi-enclosed between headlands (natural capes or promontories), see Fig. 1. They are called 'embayed beaches' or 'headland-bay beaches'. Small embayed beaches are often called 'pocket beaches'. Pockets beaches sheltered by headlands or breakwaters that restrict the opening to the sea, are called coves. If access from the land side is possible, natural embayed beaches are highly valued by tourists because of the spectacular scenery. This is less the case when they are created artificially by isolating part of a linear beach between long groynes.

Embayed beaches in general do not receive much sediment from the hinterland. Beach sediment is mainly derived from local sources (cliff erosion, for instance); therefore no strong correlation exists between grainsize and wave intensity. Headlands that protrude far into the sea (at least about 150 m) block the littoral drift and thus sediment exchange with adjacent coastal stretches. Only under severe storm conditions can sediment pass the headlands. The beach exchanges sand with the shoreface, depending on fluctuations in the wave climate (high-energy storm waves or low-energy swell). The presence of a beach implies that net offshore loss of sediment is limited (otherwise no beach would be present). Hence, the budget of the sand body comprised between the headlands is virtually closed.

Shoreline fluctuation and beach rotation

Fig. 2. Schematic representation of the typical equilibrium planform of an embayed beach with oblique wave incidence.

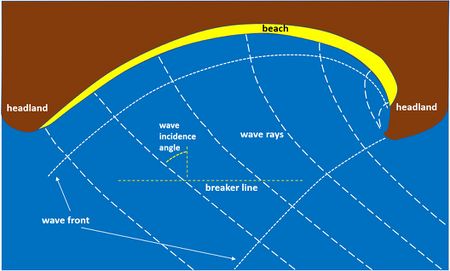
The shoreline orientation and planshape of embedded beaches depend primarily (more than for non-embedded beaches) on the offshore wave incidence direction, on wave refraction over depth contours and on wave diffraction at the headlands. Temporary shifts in the mean wave incidence angle create littoral drift that redistributes sediment along the beach and thus changes the shoreline orientation. The mean wave incidence angle that most determines littoral drift is the direction of the refracted and diffracted waves just landward from the breakerline, where longshore transport is greatest (Fig. 2). This wave incidence angle, together with the dissipation of wave energy caused by wave breaking, determines the sediment transport gradients along the beach (see Shallow-water wave theory and Littoral drift and shoreline modelling for more detailed explanations).

Fig. 3. Example of beach rotation, Palm Beach, Australian east coast. In 2013 the beach width was greatest in the southern part; in 2014 the width was greatest in the northern part. Images Google Earth.

Because the longshore drift vanishes at the headlands, a strong gradient in sand transport along the beach arises when the average direction of the incident waves shifts from a perpendicular to an oblique angle with the shoreline. Sand transport is greatest at the location where the angle is most oblique; the gradient is positive (transport divergence) on the updrift side of this location and negative (transport convergence) on the downdrift side. The resulting sand redistribution induces shoreline rotation; the updrift side retreats and the downdrift side progrades (Fig. 3). Accretion and erosion can be significant in response to seasonal changes in the mean wave direction. Significant accretion and erosion can also occur over shorter periods with high wave energy. A directionally fluctuating wave climate can lead to substantial beach rotation events from the timescale of storm duration to the decadal timescale.

The mean shoreline orientation near the downdrift headland (the headland in the wave direction) is approximately perpendicular to the mean wave direction, because of the zero drift condition. The shoreline is curved toward the updrift headland, as a result of wave diffraction at this headland. When the directional spread of incident waves is small, strong wave diffraction leads to a strongly curved shoreline (Fig. 2). For greater directional spread the shoreline curvature is less since refraction dominates over diffraction.

Rotation is not the only mode of shoreline change. Shoreline advance and retreat can also be due to seasonal or storm-induced fluctuations in wave energy and wave period that redistribute sand between beach and shoreface, similar as for non-embayed beaches, see Shoreface profile. Cross-shore processes may also induce the formation of longshore bars and rip cells. Strong rip currents can occur near the headlands; rips associated with gaps between nearshore sandbars often occur on wide embayed beaches, see Rhythmic shoreline features. Fluctuations in the shoreline position are generally more strongly related to cross-shore sand redistribution processes than to longshore sand redistribution and associated shoreline rotation.

Another phenomenon observed on some embayed beaches is the reflection of edge waves off the headlands. This may occur in particular on steep coarse-grained, reflective-type beaches under close to shore-normal wave incidence. The resulting standing wave pattern stimulates the development of beach cusps.

Beach rotation modelling

Simulation of the morphological adaptation of embayed beaches to changes in the wave climate requires a two-dimensional morphodynamic process model, if not only beach rotation but also other cross-shore and longshore sediment exchange processes play a role. These models can deal with complex topography and wave spectrum but are costly for the simulation of long-term processes such as the evolution towards equilibrium. If beach rotation is the main subject of interest, simpler models can be used, provided data is available for calibration of the model parameters. Such simpler models require additional assumptions, for example

• the wave climate can be characterized during successive short time intervals by a significant wave height [math]H_s[/math], peak wave period [math]T_p[/math] and mean wave incidence angle [math]\theta[/math];
• for each wave incidence angle [math]\theta[/math] the corresponding equilibrium shoreline angle [math]\phi_{eq}[/math] is given by the linear relationship, [math]\phi_{eq} = a \theta + b[/math], where [math]a, b[/math] are independent of [math]\theta, H_s, T_p[/math];
• the relaxation time [math]T[/math] is inversely proportional to the wave power, [math]T=c / P, \; P= T_p \, H_s^2 [/math].

The shoreline orientation [math]\phi[/math] at time [math]t[/math] can then be computed from the equation

[math]\Large\frac{d \phi}{dt}\normalsize = \Large\frac{1}{T}\normalsize (\phi_{eq}-\phi) . \qquad (1)[/math]

The values of the parameters [math]a, b, c[/math] can be obtained through fitting Eq. (1) to data for a sufficiently long period in which shoreline orientation observations are available.

Equilibrium planform

The shoreline will adopt an equilibrium shape if the wave climate remains stable over a sufficient long period. This period depends on the mean wave power and bay length. The offshore wave climate generally fluctuates on timescales which are shorter than required for equilibrium. Variation in the mean incidence direction of refracted waves may also occur over longer periods because depth contours on the less active coastal zone adapt slowly to wave climate fluctuations. Hence, the shoreline is usually in a transitional state, continuously adapting to changes in wave direction and intensity.

Even if the equilibrium conditions are not fully met, the planform of embayed beaches has a characteristic shape under oblique wave incidence. Several models have been developed to describe this planform. The equilibrium planform depends primarily on the mean wave incidence direction. Wave period and wave energy play only a secondary role. Equilibrium models are based on the assumption that the total sediment balance is closed, i.e. the embayed beach neither receives nor loses sediment across the longitudinal or transverse boundaries. The models have parameters that have to be adjusted for each specific site. Distinctive site characteristics are the presence and geography of hard bathymetric structures that modify the incident wave field by reflection, diffraction and refraction. The predictive power of the models relates to the response of the beach planform (essentially beach rotation) to variations in the mean wave incidence direction.

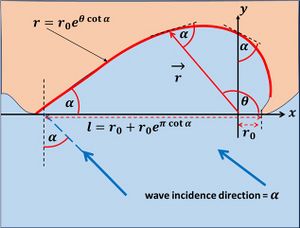
Logspiral planform

Fig. 4. Sketch and symbols for the logspiral plan shape formula, assuming equilibrium and ignoring wave refraction outside the embayment.

The logspiral shape is sketched in Fig. 2 and visible in the example shown in Fig. 3. Embayed beaches under influence of wave diffraction can be parameterized with the empirical formula

[math]r = r_0 \exp(\theta \cot \alpha) , \qquad (2)[/math]

where [math]r[/math] is the length of a vector [math]\vec{r}[/math] with components [math](x(\theta)=r \cos \theta, y(\theta)=r \sin \theta)[/math], see Fig. 4 for definitions. The theoretical diffraction point is situated at [math]x=0, y=0[/math] and the tip of the headland at [math]x=r_0, y=0[/math]. The parameter [math]\alpha[/math] is the angle between the vector [math]\vec{r}[/math] and the tangent to the curve defined by Eq. (2), because [math]dy/dx=\tan(\theta + \alpha)[/math]. In the case of morphologic equilibrium, the parameter [math]\alpha[/math] equals the wave incidence direction relative to the bay orientation if refraction outside the embayment can be ignored. The parameter [math]r_0[/math] can be derived from the embayment length [math]l[/math] as shown in Fig. 4. Embayments that are not too wide, with headlands that are not too far protruding, can be described by the logspiral shape. The logspiral shape can be justified theoretically for simple topographies and has been applied with reasonable success to many headland bay beaches shaped under influence of wave diffraction, i.e., for wave incidence angles larger than 40^o . However, the application to more complex topographies is questionable, for example if headlands protrude far offshore or if wave rays are refracted by offshore rock outcrops.

Parabolic planform

Fig. 5. Sketch and symbols for the parabolic headland bay.

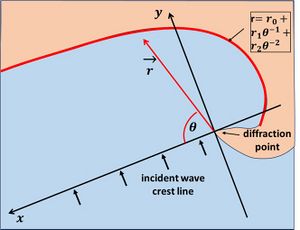
The equilibrium plan shape of embayed beaches can also be represented by a parabolic formula,

[math]r = r_0 + r_1 \theta^{-1} + r_2 \theta^{-2} . \qquad (3)[/math]

The angle [math]\theta[/math] is the angle between the wave crest line from the diffraction point (taken as the [math]x[/math]-axis) and the vector [math]\vec{r}[/math] with components [math](x(\theta)=r\cos\theta, y(\theta)=r \sin\theta)[/math], see Fig. 5. The form (3) applies to the curved updrift part of the headland-bay beach under influence of wave diffraction. It has three parameters instead of two; it is therefore more flexible than the form (2) and can accommodate more symmetrical plan forms. More symmetrical plan forms are typical for bays with far protruding headlands. The parameters [math]r_0, r_1, r_2[/math] can be derived from characteristics of the headland configuration and the wave incidence direction. However, there is no general prescription with which these parameters can be determined unambiguously; accurate determination requires least square fitting to the long-term average plan shape.

Hyperbolic tangent planform

Fig. 6. Sketch and symbols of the hyperbolic tangent representation of a headland bay.

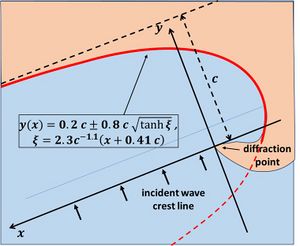
Kemp et al. (2018) have shown that the shoreline curve [math]y(x)[/math] of many wide embayed beaches can be well representaed by a formula with a single parameter [math]c[/math]. This parameter has a simple geometric interpretation: [math]c[/math] measures the cross-shore distance from the diffraction point to the shoreline where [math]dy/dx=0[/math] (headland influence vanished), see Fig. 6. It can be easily estimated from observed planforms.The formula is

[math]y(x) = 0.2 \, c + 0.8 \, c \sqrt{\tanh \xi} \; , \quad \xi = 2.3\, c^{-1.1} (x +0.41 \, c) .[/math]

This empirical formula can be applied for beaches that extend downdrift beyond the influence of the updrift headland.

Numerical modelling

The predictive power of empirical equilibrium models is limited by the many underlying assumptions and the need to adjust parameters for each specific site. Numerical models that include descriptions of all relevant hydrodynamic and geomorphological processes do not have such limitations, but require large computational resources and extensive data on boundary conditions and bathymetry. If cross-shore transport processes can be ignored, much simpler one-line or two-line models can be used, as described in the article Littoral drift and shoreline modelling. The models for sediment transport and beach development need to be dynamically coupled to hydrodynamic models of wave breaking, diffraction and reflection. Process-based models do not yield direct equilibrium morphologies, but compute the morphological evolution towards equilibrium. The most suitable model depends on the requirements of the practical problem to be addressed.

Related articles

Cove

Littoral drift and shoreline modelling

Diffraction

References

The main author of this article is Job Dronkers Please note that others may also have edited the contents of this article. Citation: Job Dronkers (2025): Embayed beaches. Available from http://www.coastalwiki.org/wiki/Embayed_beaches [accessed on 21-06-2025] For other articles by this author see Category:Articles by Job Dronkers For an overview of contributions by this author see Special:Contributions/Dronkers J