Difference between revisions of "Definitions of coastal terms"

From Coastal Wiki
Jump to: navigation, search
Line 1: Line 1:
  
  
−
Sediment transport formulas for the coastal environment
+
{{Review
 +
|name=Job Dronkers
 +
|AuthorID=120
 +
}}
  
  
  
−
==Introduction==
+
This article gives an overview of terminology frequently used in the Coastal Wiki. Many definitions are derived from Mangor et al. 2017 <ref> Mangor, K., Drønen, N. K., Kaergaard, K.H. and Kristensen, N.E. 2017. Shoreline management guidelines. DHI https://www.dhigroup.com/marine-water/ebook-shoreline-management-guidelines
 +
</ref>. Terms related to the coastal profile are illustrated in the figure below.
  
−
Calculating nearshore sediment transport is a challenge due to the complexity of the hydrodynamics and the variety of the governing phenomena. Indeed, it is very difficult to estimate sediment fluxes on beaches due to the combination of steady flows (currents) and oscillatory flows (waves). Moreover, many other effects should be integrated such as the variations in mean water level (tide,
+
__NOTOC__
−
set-up, set-down), breaking wave effects (turbulence, undertow), and topographic influence (mean slope and bed forms). Furthermore, these parameters induce different types of transport (bed load, suspended load and sheet flow), with very different physical implications for the movement of sand <ref name="Bag"> Bagnold, R.A., 1963. An approach of marine sedimentation. In: The Sea.  Vol. 3. M. N. Hill, Interscience, New York, pp. 507--528.</ref> and a probabilistic approach introduced by Einstein <ref name="Ein">Einstein, H.A., 1972. A basic description of sediment transport on beaches. In: Meyer, R.E. (Ed.), Waves on Beaches and Resulting Sediment Transport. Academic Press, pp. 53--93.</ref>. Most of the sediment transport formulas are functions of the bed shear stress and have been developed and calibrated on specific data sets. For example, Bijker <ref name="Bijk">Bijker, E.W., 1971. Longshore transport computation. J. Waterways Harbors Division 97, WW4, 687--701.</ref> and Bailard <ref name="Bail">Bailard, J.A., 1981. An energetic total load sediment transport model for a plane sloping beach. J. Geophysical Res. 86 (C11), 10938-10954.</ref> <ref name="BI">Bailard, J.A., Inman, D.L., 1981. An energetic bedload model for a plane sloping beach : local transport. J. Geophysical Res. 86(C11), 10938--10954.</ref> mainly validated their formula to field data for littoral drift; Van Rijn <ref name="Rijn84a">van Rijn, L.C., 1984. Sediment transport, part I: bed load transport. J. Hydraulic Division 110(10), 1431--1456.</ref><ref name="Rijn84b">van Rijn, L.C., 1984. Sediment transport, part II: suspended load transport. J. Hydraulic Division 110(11), 1613--1641.</ref><ref name="Rijn89">van Rijn, L.C., 1989. Handbook sediment transport by currents and waves. Tech. Rep. H461, Delft Hydraulics Lab., The Hague.</ref> or Camenen <ref name="CL05a"> Camenen, B., Larson, M., 2005. Bed-load transport under steady and oscillatory flow. In: Proc. Coastal Dynamics'05. ASCE, Barcelona, Spain, pp. 1--8, (CD ROM).</ref><ref name="CL08">Camenen, B., Larson, M., 2008. A general formula for noncohesive suspended sediment transport. J. Coastal Res. 24(3), 615--627.</ref> compared their formulas to a large variety of laboratory and field data; Dibajana <ref name="DW">Dibajnia, M., Watanabe, A., 1992. Sheet flow under nonlinear waves and currents. In: Proc. 23rd Int. Conf. Coastal Eng. ASCE, Venice, Italy, pp. 2015--2029.</ref><ref name="Dib"> Dibajnia, M., 1995. Sheet flow transport formula extended and applied to  horizontal plane problems. Coastal Eng. J. 38(2), 178--194.</ref> and Ribberink <ref name="RS">Ribberink, J.S., Al Salem, A.A., 1994. Sediment transport in oscillatory boundary layers in cases of rippled beds and sheet flow. J. Geophysical Res. 99(C6), 707--727.</ref><ref name="Rib">Ribberink, J.S., 1998. Bed-load transport for steady flows and unsteady oscillatory flows. Coastal Eng. 34, 52--82.</ref> compared and fitted their formula to experimental flume data, simulating cross-shore dynamics (current opposite to incoming waves) for sheet-flow conditions especially.
 
  
−
A selection of several sediment transport formulas are presented here to model [[Definitions of coastal terms#Bedload|bedload]], suspended load and typical phenomena observed on the nearshore such as phase-lag effects in [[Definitions of coastal terms#Sheet flow|sheet-flow]] transport.
 
  
  
−
==[[Definitions of coastal terms#Bedload|Bedload transport]] under waves and currents==
+
[[Image:DefinitionsCoastalTerms.jpg|thumb|center|700px|Fig. 1. Definition of coastal terms, adapted from Shore Protection Manual, 1984.<ref>Coastal engineering Research Center, Department of the Army, Waterways Experiment Station, 1984. "Shore protection manual".</ref>]]
  
  
−
===Bijker (1971) formula===
+
===Accretion or Aggradation===
 +
Growth (vertical and/or horizontal) of morphological features ([[#Beach|beach]], [[#Bar|bar]], [[#Dune|dune]], [[#Sand bank|sand bank]], [[#Tidal flat|tidal flat]], [[#Salt marsh|salt marsh]], [[#Tidal channel|tidal channel]], etc.) by sedimentation.
 +
===Active coastal zone===
 +
The [[active coastal zone]] (also called '''active coastal profile''') is the cross-shore coastal zone that is highly dynamic by the action of tides, [[#Wave|waves]] and wind. It extends from the [[#Closure depth|closure depth]] up to a fixed land boundary (rock, cliff, seawall, sea dike). In the case of a dune coast the front [[#Dunes|dune]] is part of the active coastal zone. See: [[Active coastal zone]]. 
 +
===Angle of incidence===
 +
The angle between the wave propagation direction and the normal to the coastline or the angle between the wave front and the coastline (often denoted <math>\alpha</math>). When [[#Wave|waves]]  enter shallow water, the wave propagation direction tends to become perpendicular to the depth contours, by [[#Refraction|refraction]].  See: [[Shallow-water wave theory]], [[Wave transformation]]. The [[#Deep water|deep water]] angle of incidence is often denoted <math>\alpha_0</math>.
 +
===Armouring===
 +
# Manmade structures such as seawalls, revetments, bulkheads, geotubes, etc. intended to prevent damage of properties situated on the coast;
 +
# The natural process of removing fine sediment from the beach or seabed top layer, leaving coarse material behind, thus leading to a more erosion-resistant residual top layer. This process may occur at places where beach or seabed material is a mixture of fine and coarse sediments (so-called '''graded sediment''').
 +
===Astronomical tide===
 +
See [[#Tide|Tide]]
 +
===Avulsion===
 +
The sudden abandonment of an existing [[#Tidal channel|tidal channel]] in favour of a newly formed channel. Channel avulsion is a common process in tidal [[#Delta|deltas]].
 +
===Backshore===
 +
The part of the beach lying between the [[#Foreshore or Beach face|foreshore]] and coastline. The backshore is dry under normal conditions; it is generally without vegetation and often characterised by berms. The backshore is only exposed to [[#Wave|waves]]  under extreme events with high tide and [[#Storm surge|storm surge]]. 
 +
===Bar===
 +
Elongated sand body created by (tidal) currents or by [[#Wave|waves]] . Bars in [[#Estuary|estuaries]] and [[#Lagoon|tidal lagoons]] develop naturally in flow convergence zones, often in relation with channel [[#Meandering|meandering]]. Estuarine bars also occur where ebb- and flood-dominated [[#Tidal channel|channels]] meet. Bars that partially block the openings to minor streams and lagoons are mainly due to [[#Littoral drift|littoral drift]]; these bars are generally referred to as [[#Spit|spits]]. Wave action is responsible for the development of [[#Breaker bar|breaker bars]], [[#Beach berm|beach berms and swash bars]]. Bars can raise above the high water level, but they are often intratidal or subtidal.
 +
===Bathymetry===
 +
Mapping of the seafloor depth with respect to the mean water level. The term is also used for the description of seafloor topography or [[#Coastal morphology|coastal morphology]]. 
 +
===Beach===
 +
The beach (or '''shore''') zone of unconsolidated material that extends from the mean low water line to the place where there is a marked change in material or physiographic form (e.g. dunefoot), or to the line of permanent vegetation (the effective limit of storm [[#Wave|waves]]  and storm surge), i.e. to the [[#Coastline|coastline]]. The beach or shore can be divided in the [[#Foreshore or Beach face|foreshore]] and the [[#Backshore|backshore]]. Often a distinction is made between [[#Dissipative and reflective beaches|dissipative and reflective beaches]].
 +
===Beach berm===
 +
A beach berm (or '''beach ridge''' or '''swash bar''') is a nearly horizontal shore parallel ridge formed on the beach due to the landward transport of the coarsest fraction of the beach material by the [[#Swash|wave uprush]]. There may be several beach berms and in some cases no berms. Under normal conditions a beach berm is formed on the upper part of the [[#Foreshore or Beach face|foreshore]], and over the [[#Backshore|backshore]] during severe events.
  
−
One of the first sediment transport formulations that is still often used in engineering applications was proposed by Bijker <ref name="Bijk"></ref>. It is derived from Frijlink's formula <ref> Frijlink, H.C., 1952. Discussion des formules de d\'ebit solide de Kalinske, Einstein, et MeyerPeter et M\"uller compte tenue des mesures r\'ecentes de transport dans les rivi\`eres n\'eerlandaises [discussion of bedload movement formulas of Kalinske, Einstein and Meyer-Peter and M\"uller and their application to recent measurements of bedload movement in the rivers of Holland]. In: Comptes rendus 2i\`eme Journée Hydraulique. Grenoble, France, pp. 98--103, (in French). </ref> for a current only with a modification of the bottom shear stress using a wave-current model. The direction of sediment fluxes is always that of the current since this formula was proposed to estimate longshore transport rate. Bedload transport <math>q_{sb}</math> is expressed such as:
+
Berms can also form on the higher intertidal zone of a beach or a [[#Tidal flat|tidal flat]]; these berms are generally called "swash bars". They may be related to onshore moving [[#Breaker bar|breaker bars]].
 +
===Beach cusps===
 +
Regularly spaced shoreline structures (spacing typically between a few meters and a few tens of meters) consisting of small embayments between protruding horns. They are a common feature of [[#Dissipative and reflective beaches|reflective beaches]]. See: [[Beach Cusps]].
 +
===Beach face===
 +
See [[#Foreshore|Foreshore]]
 +
===Beach fill===
 +
The supply of beach sand for the construction of an artificial beach.
 +
===Beach park===
 +
A beach park is a scheme which consists of new artificial beaches, stabilising coastal structures and filling/reclamation, which in combination provides new recreational facilities. Artificial beaches will be exposed to wave action and will evolve to a stable plan and profile shape.
 +
===Bed forms===
 +
The seafloor is seldom flat, but generally undulated by the interaction with currents and [[#Wave|waves]] . Undulated bedforms exist over a large range of spatial scales, from centimeters up to kilometers, see: [[Wave ripples]], [[Wave ripple formation]], [[Sand ridges in shelf seas]], [[Stability models]]. The smallest bedforms play an important role in the friction exerted by the seabed on water motion, see [[#Boundary layer|Boundary layer]], [[Bedforms and roughness]], [[Bed roughness and friction factors in estuaries]], [[Wave ripples]], [[Wave ripple formation]].
 +
===Bedload===
 +
Bedload transport refers to sediment transport by rolling and saltating sediment grains over the seabed. Bedload transport is the dominant sediment transport mode when the flow velocities (currents and wave-orbital velocities) are above the critical velocity for setting bed particles in motion (in the order of 0.2-0.4 m/s for sandy sediments), but insufficient for bringing sediment particles in suspension. Bedload transport occurs for non-cohesive medium-coarse sediments and is associated with the formation of bed ripples and dunes. The migration of these bedforms yields an estimate for the bedload  transport. See: [[Sand transport]].
 +
===Benthos===
 +
Organisms living on or in the seabed, including vegetation.
 +
===Boundary layer (turbulent)===
 +
The fluid layer where momentum and energy are dissipated as a result of friction exerted by the seafloor or a nearby hard boundary. In the boundary layer, fluid momentum is dissipated through transfer from the large-scale flow pattern in a cascade process to increasingly smaller [[#Turbulence|turbulent]] flow structures. The large-scale flow profile in the turbulent boundary layer has a logarithmic profile. The thickness of the turbulent boundary layer corresponds to the size of the largest turbulent eddies generated by friction at the seafloor. Because the development of the turbulent boundary layer takes time, the boundary layer thickness for slowly varying currents is much greater than for rapidly varying currents. The boundary layer thickness for steady flow and tidal flow is typically of the order of 10-50% of the water depth, whereas the boundary layer thickness for wind-driven [[#Wave|waves]]  is only a few centimeters. Hence, steady flow and tidal flow experience much stronger friction than propagating wind-driven waves. See: [[#Bed forms|Bed forms]], [[Wave ripples]].
 +
===Breaker zone===
 +
The breaker zone (or '''surf zone''') is the part of the shoreface exposed to depth-limited [[#Wave breaking|breaking waves]], see Fig. 1. The outer limit of the breaker zone (or surf zone) is called the '''breaker line'''. However, the instantaneous width of the breaker zone varies with the instantaneous wave conditions and water level. In the general context, the surf zone width is defined in relation to the yearly wave climate defined by the significant wave height <math>H_{s,12h/y}</math>, which is the [[#Wave height|wave height]] exceeded 12 hours per year. The surf zone thus corresponds to the zone where waves of height <math>H_{s,12h/y}</math> break. The surf zone is somewhat narrower than the [[#Shoreface|littoral zone]]. It is estimated that 80 to 90% of the yearly littoral transport takes place within the breaker or surf zone.
 +
===Breaker bar===
 +
A submerged shore parallel embankment of sand or gravel built in the [[#Breaker zone|breaker zone]] due to the action of [[#Wave breaking|breaking waves]] and cross-currents. There can be several rows of bars. Breaker bars are very mobile formations, which tend to be in unstable equilibrium with actual wave and tide conditions, which means that they are constantly changing. The overall tendency is that the bars are moving seawards during storm wave conditions and landwards during conditions dominated by smaller [[#Wave|waves and swell]]. At intervals there are gaps in the breaker bars formed by [[#Rip currents|rip currents]]. 
 +
===Breakwater===
 +
A structure built for reducing wave activity in the waters at the leeside. It can be linked to the shore or it can be positioned offshore. A common type is the '''detached breakwater'''. This is a structure approximately parallel to the coast, built inside or outside the surf zone. The main purpose of detached breakwaters is either to protect a harbor entrance or a ship wharf from wave action or to reduce wave activity at the beach. See: [[Application of breakwaters]], [[Detached breakwaters]], [[Detached shore parallel breakwaters]], [[Floating breakwaters]].
 +
===Buoyancy===
 +
Upward force experienced by a body of lower density (water body of lower salinity, higher temperature, for example) than the surrounding fluid.
 +
===Chenier===
 +
An accretionary feature consisting of a long, low lying, narrow strip of gravelly sand (typically up to 3 m high and 40 to 400 m wide), often shelly, deposited in the form of wave-built beach ridge on a swampy, deltaic, or alluvial coastal plain of fine sediment.
 +
===Closure depth===
 +
The depth beyond which no significant longshore or cross-shore transports take place due to littoral transport processes. The closure depth can thus be defined as the depth at the seaward boundary of the [[#Shoreface|littoral zone]], see: [[Closure depth]].
 +
===Coast===
 +
The strip of land that extends from the coastline inland to the first major change in the terrain features, which are not influenced by the coastal processes. The main types of coastal features are dunes, cliffs and low-lying areas, possibly protected by dikes or seawalls.
 +
===Coastal area===
 +
The land and sea areas bordering the shoreline.
 +
===Coastal cell===
 +
See [[#Sediment cell|Sediment cell]]
 +
===Coastal development===
 +
Any activity likely to alter the physical nature of the [[#Coastal zone|coastal zone]] in any way, including construction of buildings and works, the deposit of waste or other material from outfalls, vessels or by other means, the removal of sand, sea shells, natural vegetation, sea grass and other substances, dredging and filling, land reclamation and mining or drilling for minerals, but excluding fishing activities.
 +
===Coastal erosion===
 +
Distinction must be made between incidental coastal erosion and ongoing coastal erosion.  
 +
*'''Incidental coastal erosion''' (also called '''temporal coastal erosion''') takes place mainly by cross-shore processes during extreme events (high water levels, high waves), which produce beach lowering or scouring in the foot of the cliffs or in the foot of the dunes (see [[#Wave run-up|wave run-up]] and [[dune erosion]]). For stable coasts, incidental erosion is a reversible process; under average conditions the coastal profile is restored - see: [[Dealing with coastal erosion]], [[Natural causes of coastal erosion]] and [[Active coastal zone]].
 +
*'''Ongoing coastal erosion''' (also called '''structural coastal erosion''' or '''long-term coastal erosion''') is mainly due to a structural imbalance in the supply and export of material from a certain coastal section. Erosion takes place on the [[#Shoreface|shoreface]] and on the beach if the export is greater than the supply of material. The deficit can be due to both cross-shore processes and [[#Littoral drift|longshore processes]]. The main reason for a long-term erosional trend is often a deficit in the littoral drift budget, caused by a down-drift increase of [[#Littoral drift|longshore sediment transport]], see: [[Littoral drift and shoreline modelling]]. The rate of erosion is expressed in volume/length/time, e.g. in m<sup>3</sup>/m/year, but erosion rate is often used synonymously with coastline retreat, and thus expressed in m/year. See:  [[Natural causes of coastal erosion]], [[Human causes of coastal erosion]], [[Types and background of coastal erosion]], [[Accretion and erosion for different coastal types]], [[Typical examples of structural erosion]], [[Dune erosion]].
 +
===Coastal hinterland===
 +
The land that extends landward of the coast and which is not influenced by coastal processes.
 +
===Coastal morphology===
 +
Coastal morphology (or '''coastal geomorphology''' or '''morphology''') is the science of natural morphodynamic processes, which are responsible for shaping the [[#Coastal zone|coastal zone]]. The meaning of the Greek word "morphè" is form or shape. These natural processes, which involve wind, tides, currents, waves, biota, [[#Sea-level rise|soil and sea-level changes]], interact with the materials from which the coastal zone is built; this interaction is called '''coastal morphodynamics'''. Coastal zones around the world are shaped in highly diverse ways. The term coastal morphology is also used for the description of these very diverse coastal forms. See also: [[Characteristics of sedimentary shores]], [[Classification of coastlines]].
 +
===Coastal profile===
 +
The cross-shore profile of the [[#Active coastal zone|active coastal zone]]. See also: [[Shoreface profile]].
 +
===Coastal protection===
 +
Three different protection/defence definitions are used as follows:
 +
*'''Coastal protection''': Measures aimed at protecting the coast against coastline retreat, thus protecting settlements, infrastructure, the [[#Coast|coast]] and the [[#Coastal hinterland|hinterland]] from erosion often at the expense of losing the beach and the dynamic coastal landscape. Coastal protection often consists of hard structures such as revetments, [[#Breakwater|breakwaters]] or [[#Groyne|groynes]], see also:  [[Hard coastal protection structures]], [[Seawalls and revetments]].
 +
*'''Sea defence''': Measures aiming at protecting low-lying coast and coastal hinterland against flooding caused by the combined effect of storm surge and high astronomical tides. Sea defence often consists of dikes or seawalls of some kind, or artificial [[Dunes|dunes]], see: [[Overtopping resistant dikes]].
 +
*'''Shore protection''': Measures aiming at protecting, preserving or restoring the shore and the dynamic coastal landscape as well as protecting against coastline retreat to the extent possible. See: [[Soft shoreline protection solutions]], [[Artificial reefs]], [[Natural barriers]], [[Dynamics, threats and management of biogenic reefs]], [[Sand-filled geosystems in coastal engineering]], [[Beach nourishment]], [[Artificial nourishment]], [[Shore nourishment]], [[Beach drainage]], [[Dynamics, threats and management of dunes]].
 +
===Coastal zone===
 +
General, wide planning-oriented characterisation: The interface between land and sea, defined as the part of the land affected by its proximity to the sea (influence of marine processes), and the part of the sea affected by its proximity to the land (influence of terrestrial processes).
 +
===Coastal zone management (CZM)===
 +
The aim of coastal zone management is to balance the different interests of coastal areas, which are related to: safety, environment, economy, human activities and esthetic and cultural values, see also: [[Integrated Coastal Zone Management (ICZM)]] and [[Some definitions of Integrated Coastal Zone Management (ICZM)]]. Because of this comprehensive scope the term '''Integrated coastal zone management (ICZM)''' is more widely used than CZM. The dynamic nature of the coastal zone is a highly challenging aspect of coastal zone management. Coastal engineering (hard or soft measures) and coastal area planning are major instruments for coastal zone management. See: [[The Integrated approach to Coastal Zone Management (ICZM)]], [[Spatial Planning and Integrated Coastal Zone Management]], [[Policy instruments for integrated coastal zone management]], [[Shoreline management]].
 +
===Coastline===
 +
Technically the line that forms the boundary between the [[#Coast|coast]] and the [[#Beach|shore]], i.e. the foot of the cliff or the foot of the dunes. Commonly, the line that forms the boundary between the land and the water. See also: [[Classification of coastlines]].
 +
===Coastline retreat===
 +
Landward shift of the coastline caused by a long-term erosional trend or by sea-level rise.
 +
===Continental shelf===
 +
The continental shelf (or '''shelf sea''') is the continental border which is submerged in relatively shallow sea (water depths typically less than 200 m). The continental shelf extends from the coastline of a continent to a drop-off point called the shelf break. From the break, the shelf descends toward the deep ocean floor in what is called the continental slope. Water motion, water quality and ecosystem of shelf seas are strongly influenced by the adjacent ocean, see [[Shelf sea exchange with the ocean]].
  
−
<math>    q_{sb} =  C_b \ d_{50} \ \sqrt{\Large \frac{\mu_c \tau_c}{\rho}} \normalsize \exp\left( -0.27 \ \Large \frac{(\rho_s-\rho)gd}{\mu_c \tau_{cw}} \normalsize \right)  \qquad (1) </math>
+
The legal definition of a continental shelf is different than the geographic one. According to the UN Convention on the Law of the Sea, every nation has a continental shelf extending no more than 200 nautical miles from the nation's coastline. See: [[Legislation for the sea]].  
−
 
+
===Coriolis===
−
where <math>d_{50}</math> is the median grain size diameter, <math>h</math> the water depth, <math>C_b</math> a breaking wave parameter, <math>\mu_c</math> a ripple parameter, <math>\tau_c</math> the skin shear stress due to current only, <math>\tau_{cw}</math> the shear stress due to wave-current interaction, and <math>\rho_s</math>, <math>\rho</math> the sediment and water densities, respectively.
+
The acceleration experienced by a current due to earth rotation, see: [[Coriolis acceleration]].
−
 
+
===Creek===
−
The shear stress due to the wave-current interaction is computed following the method proposed by Bijker <ref name="Bijk"></ref> introducing waves as a stirring factor:
+
A [[#Tidal channel|tidal channel]] that drains a [[#Salt marsh|salt marsh]].
−
 
+
===Deep water===
−
<math> \tau_{cw} = \left[ 1+0.5 (\xi_B \ \Large \frac{U_w}{U_c} \normalsize )^2 \right] \ \tau_{cf} \qquad (2) </math>
+
Water too deep for [[#Wave|waves]]  to be affected by the seafloor; typically taken as half the wavelength, or greater.
−
 
+
===Delta===
−
with <math>\xi_B = \sqrt{f_{wt}/f_{ct}}</math> a parameter due to the wave-current interaction, <math>f_{wt}</math> the total friction coefficient due to waves (including bedform effects), <math>U_w</math> the peak value of the wave orbital velocity at the bottom, <math>U_c</math> the depth-averaged current velocity and <math>\tau_{cf} </math> the bed shear stress (including form drag).
+
The fan-shaped mouth of a river or a tidal basin, formed by several distributary channels. They are the result of depositional and erosional processes under the influence of currents, waves and tides. Because of their different morphologies, often a distinction is made between river-dominated deltas, wave-dominated deltas and tide-dominated deltas. See: [[Morphology of estuaries]], [[Wave-dominated river deltas]].  
−
 
 
−
The ripple parameter introduced by Bijker <ref name="Bijk"></ref> is defined by the following equation:
 
−
 
 
−
<math>  \mu_c = \left(f_{ct}/f_c \right)^{3/2}  \qquad (3)</math>
 
−
 
 
−
where <math>f_{ct}</math> is the total friction coefficient due to current (including bedform effects) and <math>f_c</math> is the skin friction coefficient due to current.
 
−
 
 
−
The breaking wave coefficient is defined by:
 
−
 
 
−
<math> C_b = 2 , \; H_w/h < 0.05 ; \quad C_b = 2 + 3 \ (H_w/h-0.05) , \; 0.05<H_w/h<0.4 ; \quad C_b = 5 , \; 0.4<H_w/h .
 
−
\qquad (4) </math>
 
−
 
 
−
where <math>H_w</math> is the wave height, and <math>h</math> the water depth.
 
−
 
 
−
 
 
−
 
 
−
===Bailard and Inman (1981) formula===
 
−
 
 
−
Bagnold <ref name="Bag"></ref> introduced the energetics model in which the main idea is that the sediment flux is proportional to the energy flux <math>\Omega</math> (local rate of energy dissipation):
 
−
 
 
−
<math>  \Omega = 0.5 \ \rho \ f_{cw} \ | \overrightarrow{u(t)} |^3 \qquad (5)</math>
 
−
 
 
−
with <math>f_{cw}</math> the friction coefficient due to the wave-current interaction, <math>\vec{u(t)}</math> the  instantaneous velocity vector, <math>\vec{u(t)} = \vec{U_c} +  \vec{u_w(t)}</math>, <math>U_c</math> the depth-averaged current velocity, and <math>u_w(t)</math> instantaneous wave velocity over the bed.
 
−
 
 
−
The Bailard and Inman formula <ref name="BI"></ref> is derived directly from  the Bagnold model. For a horizontal bed, it can ultimately be written as a vector of sediment volume transport:
 
−
 
 
−
<math>  \overrightarrow{q_{sb}} =  \Large \frac{0.5 \ f_{cw}}{g \ (s-1)} \normalsize \left( \Large \frac{\epsilon_b}{\tan\phi} \normalsize <\mid\vec{u}\mid^2\vec{u}> \right) \qquad (6)</math> 
 
−
 
 
−
where <math>\epsilon_b</math> is the bed load efficiency, <math>\phi</math> the  friction angle of the sediment, <math>s</math> the ratio of sediment and water densities, and <math>< \ ></math> yields an average over several periods of the wave.
 
−
 
 
−
The bed load efficiency was found slightly different from the one given by Bagnold <ref name="Bag66">Bagnold, R.A., 1966. An approach of sediment transport model from general physics. Tech. Rep. 422-I, US Geol. Survey Prof. Paper. </ref>. Bailard suggested from a calibration with field data that <math>\epsilon_b = 0.1</math>.
 
−
One difficulty for this formulation is the estimation of the friction coefficient due to the wave-current interaction as Bailard <ref name="BI"></ref> did not specify any expression for this friction factor.
 
−
 
 
−
 
 
−
===Van Rijn (1989) formula===
 
−
 
 
−
The Van Rijn formula <ref name="Rijn84a"></ref><ref name="Rijn89"></ref> is expressed in the same way as the Bijker formula, as a bed load formula taking into account the influence of waves as a stirring effect.  The direction of sediment fluxes is also that of the current. Bedload transport can be written as follows:
 
−
 
 
−
 
 
−
<math>  q_{sb} = 0.25 \ d_{50} \ d_*^{-0.3} \ (\tau_{cw}/ \rho)^{0.5} \ \left( \tau_{cw} / \tau_{cr} \ - 1 \right) \qquad (7)</math>
 
−
 
 
−
 
 
−
where <math>d_* = [(s-1)g/\nu^2]^{1/3}d_{50}</math> the dimensionless sediment diameter, <math>\tau_{cw} = 0.5 f_{cw} U_{cw}</math> the skin bed shear stress due to current and waves with <math>f_{cw}=\alpha \beta u_c + (1-\alpha) U_w</math> , <math>\alpha = u_c/(u_c+U_w)</math>, <math>u_c</math> is the current close to the bottom as defined by Van Rijn <ref name="Rijn89"></ref>, <math>\beta</math> an offset coefficient for bedload, and <math>\tau_{cr}</math> the critical bed shear stress for inception of movement.
 
−
 
 
−
Van Rijn <ref name="Rijn07a"> van Rijn, L.C., 2007. Unified view of sediment transport by currents and waves. I: Initiation of motion, bed roughness, and bed-load transport. J. Hydraulic Eng. 133(6), 649—667.</ref> updated his bedload formula. He proposed a new simplified bedload transport formula for steady flow (with or without waves):
 
−
 
 
−
 
 
−
<math>  q_{sb} = 0.015 \ U_c \ h \; (\large \frac{d_{50}}{h})^{1.2} \normalsize \ \Psi^{1.5} \qquad (8) </math>
 
−
 
 
−
 
 
−
where <math>\Psi=(U_e-U_{cr})/\sqrt{(s-1)gd_{50}}</math> is the mobility parameter, <math>U_e=U_c+\gamma U_w</math> the effective velocity with <math>\gamma=0.4</math> for irregular waves and <math>\gamma=0.8</math> for regular waves, <math>U_{cr}</math> the critical effective velocity for inception of movement.
 
−
 
 
−
 
 
−
===Ribberink (1998) formula===
 
−
 
 
−
Ribberink <ref name="Rib"></ref> proposed a quasi-steady model of bed load transport where the instantaneous solid flux is assumed to be proportional to a function of the difference between the actual time-dependent bed shear stress and the critical bed shear stress (see Fig. 1). This formulation has been calibrated towards several flume data sets including wave-current interaction in a plane regime (suspended load negligible) and field data (unidirectional flows in rivers).
 
−
 
−
[[Image:CamFig1.jpg|thumb|700px|center|Figure 1:  Profile of the time-dependent velocity (a) and bed shear stress (b) in the wave direction (an angle <math>\varphi</math> exists between the current and wave directions).]]
 
−
 
 
−
The following expression for the sand transport rate was obtained:
 
−
 
 
−
<math>  \vec{q_{sb}} = m_{Rib} \ \sqrt{(s-1) \ g \ d_{50}^3} \  <( |\vec{\theta(t)}|- \theta_{cr})^{n_{Rib}}  \Large \frac{\overrightarrow{\theta(t)}}{|\theta(t)|} \normalsize > \qquad (9) </math>
 
−
 
 
−
where <math>\overrightarrow{\theta(t)} = 0.5 \ f_{cw} \ |u(t)|\overrightarrow{u(t)} \ / \  [(s-1) \ g \ d_{50}]</math> is the  time-dependent Shields parameter ({\it cf.} figure 1)  with the instantaneous velocity <math>\overrightarrow{u(t)} = \vec{U_c} + \overrightarrow{u_w(t)}</math> and the wave-current friction factor <math>f_{cw}</math>, <math>\theta_{cr}</math> the critical Shields parameter, <math>< \ ></math> yields a time-averaging over several wave periods, and <math>m_{Rib}=11</math>, <math>n_{Rib}=1.65</math> the adjusted coefficients.
 
−
 
 
−
In the same way as the Bailard formula, an equivalent wave-current friction coefficient has to be computed. Ribberink used the Madson and Grant model <ref> Madsen, O.S., Grant, W.D., 1976. Sediment transport in the coastal environment. Tech. Rep. 209, M. I. T., Cambridge, Massassuchetts, USA.</ref> model for which the friction coefficient <math>f_{cw}</math> due to the wave and current interaction is defined such as:
 
−
 
 
−
<math>  f_{cw}=X_v \ f_c +(1-X_v) \ f_w  \qquad(10) </math>
 
−
 
 
−
with <math>X_v=|U_c|/(|U_c|+U_w)</math>.
 
−
 
 
−
Ribberink also proposed to compute total roughness values as follows:
 
−
 
 
−
<math>  k_{st} = {\rm max} \left( k_s;d_{50} \ [1+6 \ (<|\theta(t)|> / \theta_{cr}-1)] \right)  \qquad (11)</math>
 
−
 
 
−
where <math>k_s</math> is skin roughness height.
 
−
 
 
−
Formulas with a similar approach have been suggested by Soulsby and Damgaard <ref>Soulsby, R.L., Damgaard, J.S., 2005. Bedload sediment transport in coastal waters. Coastal Eng. 52, 673—689</ref> and Gonzalez and Madsen <ref>Gonzalez-Rodriguez, D., Madsen, O.S., 2007. Seabed shear stress and bedload transport due to asymmetric and skewed waves. Coastal Eng. 54, 914—929.</ref>.
 
−
 
 
−
 
 
−
===Camenen and Larson (2005) formula===
 
−
 
 
−
Camenen and Larson <ref name="CL05a"></ref>  developed a formula for bed load transport in a similar approach as Ribberink. They introduce an exponential function for the effect of inception of motion following the probabilistic approach introduced by Einstein <ref name="Ein"></ref>. The bed load transport <math>q_{sb}</math> may be expressed as follows:
 
−
 
 
−
<math>  q_{sbw} =  a_w \ \sqrt{(s-1)g \ {d_{50}}^3} \ \sqrt{\theta_{cw,net}} \ \theta_{cw,m} \ \exp\left( -b \Large \frac{\theta_{cr}}{\theta_{cw}} \normalsize \right) , </math>
 
−
 
 
−
<math>  q_{sbn} =  a_n \ \sqrt{(s-1)g \ {d_{50}}^3} \ \sqrt{\theta_{cn}} \ \theta_{cw,m} \  \exp\left( -b \Large \frac{\theta_{cr}}{\theta_{cw}} \normalsize \right) .  \qquad (12) </math>
 
−
 
 
−
where the subscripts <math>w</math> and <math>n</math> correspond, respectively, to the wave direction and the direction normal to the wave direction and <math>a_w</math> <math>a_n</math> and <math>b</math> are empirical coefficients. <math>\theta_{cw,m}</math> is the mean Shields parameter and <math>\theta_{cw}</math> the maximum Shields parameter due to wave-current interaction, and  <math>\theta_{cn}= \frac{1}{2} f_c (U_c \sin\varphi)^2 / ((s-1)g d_{50})</math>. In order to simplify the calculations, the mean and maximum Shields parameter due to wave-current interaction is obtained by straightforward addition:
 
−
 
 
−
<math>\theta_{cw,m} = ( {\theta_c}^2 + {\theta_{w,m}}^2 + 2 \theta_{w,m} \theta_c \cos\varphi)^{1/2}</math>
 
−
 
 
−
<math>\theta_{cw} = ( {\theta_c}^2 + {\theta_w}^2 + 2 \theta_w \theta_c \cos\varphi)^{1/2}</math>,
 
−
 
 
−
respectively, where <math>\theta_c</math>, <math>\theta_{wm}</math>, and <math>\theta_w</math> are the current, mean wave, and maximum wave Shields number, and <math>\theta_{w,m}=0.5 \theta_w</math> for a sinusoidal wave profile.
 
−
 
 
−
The net sediment transporting velocity <math>\theta_{cw,net}</math> in Eq. 12 is given by,
 
−
 
 
−
<math>  \theta_{cw,net} = \theta_{cw,on}+\theta_{cw,off} \qquad (13) </math>
 
−
 
 
−
where <math>\theta_{cw,on}</math> and <math>\theta_{cw,off}</math> are the mean values of the instantaneous shear stress over the two half periods <math>T_{wc}</math> and <math>T_{wt}</math> (<math>T_w=T_{wc}+T_{wt}</math>, in which <math>T_w</math> is the wave period) defined as follows (see Fig. 1),
 
−
 
 
−
<math> \theta_{w,onshore} =    \Large \frac{1}{2T_{wc}} \int_0^{T_{wc}} \frac{f_{cw} (u_w(t)+U_c\cos\varphi)^2}{(s-1)g d_{50}} \normalsize dt ,  </math>
 
−
 
 
−
<math>  \theta_{w,offshore}  =    \Large \frac{1}{2T_{wt}} \int_{T_{wc}}^{T_w} \frac{f_{cw} (u_w(t)+U_c\cos\varphi)^2}{(s-1)g d_{50}} \normalsize dt \qquad (14) </math>
 
−
 
 
−
where <math>u_w(t)</math> is the instantaneous wave orbital velocity.
 
−
 
 
−
Based on comparison with an extensive data set, the following relationship is proposed for the transport coefficient <math>a_w</math>  <ref name="CL05a"></ref><ref name="CL05b">Camenen, B., Larson, M., 2005. A bedload sediment transport formula for the nearshore. Estuarine, Coastal \& Shelf Science 63, 249--260.</ref>
 
−
 
 
−
<math>  a_w = 6 + 6 \ X_t  \qquad (15) </math>
 
−
 
 
−
in which <math>X_t = \theta_c/(\theta_c + \theta_w)</math> , where <math>\theta_c</math> and <math>\theta_w</math> are the Shields parameter for current and waves, respectively. The coefficient perpendicular to the waves, where only the current transports sediment, is set to <math>a_n = 12</math>, and the coefficient in the term describing initiation of motion is <math>b = 4.5</math>.
 
−
 
 
−
 
 
−
==Phase-lag effects in [[Definitions of coastal terms#Sheet flow|sheet-flow]] transport==
 
−
 
 
−
Since the experiments of Dibajnia and Watanabe <ref name="DW"></ref> and Ribberink and Salam <ref name="RS"></ref>, one realized that for intense sheet-flow transport, net bedload in the wave direction could be reduced or even be switched to the opposite direction of waves due to the phase-lag between sediment concentrations and fluid velocities <ref> Dohmen-Janssen, M., 1999. Grain size influence on sediment transport in oscillatory sheet flow, phase-lags and mobile-bed effects. Ph.D. thesis, Delft Univ. of Technology, The Netherlands, ISBN 90-9012929-4.</ref>. Several authors attempt to model these effects.
 
−
 
 
−
===Dibajnia and Watanabe (1992) formula===
 
−
 
 
−
The sediment transport formulation of Dibajnia and Watanabe <ref name="DW"></ref> is the first one to include phase-lag effects. Similar to the Bailard  and Ribberink models, it breaks down the sediment transport into two half-cycles due to the presence of waves (see Fig. 2). During the first half-cycle, sediment moves in the direction of the wave, just as it moves in the opposite direction during the second half-cycle. An interesting aspect of the formula is that it takes into account a possible quantity of sand still in suspension after each half-cycle, and hence moving in the other direction. This formula enables transport under a non-linear wave to be described.
 
−
 
 
−
 
 
−
[[Image:CamFig2.jpg|thumb|700px|center|Figure 2:  Bottom velocity profile in the direction of the wave propagation <ref name="DW"></ref>.]]
 
−
 
 
−
The solid volume flux is given by the following equation:
 
−
 
 
−
<math>  \vec{q_s} = A_{dw} \ W_s \ d \ \Large \frac{\vec{\Gamma}}{\Gamma} \normalsize \  \Gamma^{B_{dw}}
 
−
  \qquad (16) </math>
 
−
 
 
−
with <math>A_{dw} = 0.001</math> and <math>B_{dw} = 0.55</math> the calibration coefficients, and
 
−
 
 
−
<math>  \vec{\Gamma} = \Large \frac{ T_{wc} \ \vec{u_{wc}} \ ( \Omega_c^{\ 3} + \Omega_t^{'3} ) + T_{wt} \ \vec{u_{wt}} \ ( \Omega_t^{\ 3} + \Omega_c^{'3} )} {(u_{wc}  + u_{wt}) \ T_w}  \normalsize , \qquad (17) </math>
 
−
 
 
−
where <math>T_w</math>, <math>T_{wc}</math>, <math>T_{wt}</math> are the period and half-periods of wave taking into account the effect of a current (cf. figure 2); <math>\Omega_c</math>, <math>\Omega_t</math> are the amount of sand entrained and settled during the half-period <math>T_{wc}</math> and <math>T_{wt}</math>, respectively; <math>\Omega'_c</math>, <math>\Omega'_t</math> arecthe amount of suspended sand remaining from the positive and the negative half-cycle respectively. <math>u_{wc}^2</math> and <math>u_{wt}^2</math> the average quadratic velocities (wave + current) over each half-period expressed as:
 
−
 
 
−
 
 
−
<math>  {u_{wj}}^2 = \Large \frac{2}{T_{wj}}\int_t^{t+T_{wj}} \normalsize u^2(t) \ dt + 2 \ {U_c}^2 \ sin^2\varphi  \qquad (18) </math>
 
−
 
 
−
where <math>j</math> can be <math>c</math> or <math>t</math>, <math>u(t) = U_c \ \cos\varphi + u_w(t)</math>. <math>u_w(t)</math> is the instantaneous wave orbital velocity, and <math>\varphi</math> the angle between wave direction and current direction.
 
−
 
 
−
If <math>  \omega_j \leq \omega_{cr}</math>  then <math>\Omega_j = \omega_j \ \Large \frac{2 \ W_s \ T_{wj}}{d} \normalsize </math> and <math>\Omega'_j=0,  </math>
 
−
 
 
−
If <math> \omega_j \geq \omega_{cr}</math> then <math> \Omega_j = \Large \frac{2 \ W_s \ T_{wj}}{d} \normalsize </math> and <math>  \Omega'_j= (\omega_j-1) \ \Large \frac{2 \ W_s \ T_{wj}}{d} \normalsize , \qquad (19) </math>
 
−
 
 
−
with:
 
−
 
 
−
<math>  \omega_j = \Large \frac{{u_{wj}}^2}{2 \ (s-1) \ g \ W_s \ T_{wj}} , \normalsize  \qquad (20) </math>
 
−
 
 
−
where <math>j</math> can be <math>c</math> or <math>t</math>.
 
−
 
 
−
<math>\omega_{cr}</math> is a ripple parameter defined as:
 
−
 
 
−
<math> \omega_{cr} =   0.03 \; </math>  if  <math> \; \theta_{cw(max)} \leq 0.2  ; </math> 
 
−
 
 
−
 
 
−
<math> \omega_{cr} =   1-0.97 \ [1- 6.25 \ (\theta_{cw(max)}-0.2)^2 ]^{0.5} \; </math> If  <math> \; 0.2 < \theta_{cw(max)} < 0.6 ; </math>
 
−
 
 
−
<math> \omega_{cr} = 1  \; </math> if <math> \; 0.6 < \theta_{cw(max)}  \qquad (21) </math> 
 
−
 
 
−
where <math>\theta_{cw(max)}</math> is the maximum Shields parameter due the wave-current interaction (computed following <ref name="Soul"> Soulsby, R.L., 1997. Dynamics of marine sands, a manual for practical applications. Thomas Telford, London, UK, ISBN 0-7277-2584 X.</ref>, pp.87-95).
 
−
 
 
−
Several authors developed a model based on the work of Dibajnia and Watanabe by introducing the effects of acceleration <ref name="WS">Watanabe, A., Sato, S., 2004. A sheet-flow transport rate formula for asymmetric, forward-leaning waves and currents. In: Proc. 29th Int. Conf. Coastal Eng. Lisbon, Portugal, pp. 1703—1714.</ref> and by introducing the Shields parameter in Eq.17. <ref>da Silva, P.A., Temperville, A., Seabra Santos, F., 2006. Sand transport under combined current and wave conditions: A semi-unsteady, practical model. Coastal Eng. 53, 897—913.</ref><ref>van der A, D.A., Ribberink, J.S., van der Werf, J.J., O'Donoghue, T., Buijsrogge, R.H., Kranenburg, W.M., 2013. Practical sand transport formula for non-breaking waves and currents. Coastal Eng. 76, 26--42.</ref>
 
−
 
 
−
 
 
−
===Camenen and Larson (2006) formula===
 
−
 
 
−
[[Image:CamFig3.jpg|thumb|400px|right|Figure 3:  Schematic view of the instantaneous velocity and acceleration variation for a bore over a wave period and in the direction of the waves.]]
 
−
 
 
−
Following the approach proposed by Dibajnia and Watanabe, Camenen and Larson <ref name="CL06"> Camenen, B., Larson, M., 2006. Phase-lag effects in sheet flow transport. Coastal Eng. 53, 531—542,</ref>  introduced a parameter in Eq. 13 of the bedload formula to take into account phase-lag effects in bedload transport. This modification was eventually extended to acceleration effects  <ref name="CL07">Camenen, B., Larson, M., 2007. A total load formula for the nearshore. In: Proc. Coastal Sediments'07. ASCE, New Orleans, Louisiana, USA, pp. 56--67. </ref><ref>Camenen, B., Larson, M., 2010. Discussion of "measurements of sheet flow transport in acceleration-skewed oscillatory flow and comparison with practical formulations" by D.A. van der A, T.O'Donoghue and J.S. Ribberink. Coastal Eng. 58(1), 131--134.</ref>. The net sediment transporting velocity <math>\theta_{cw,net}</math> in Eq. 12 is then given by,
 
−
 
 
−
 
 
−
<math>  \theta_{cw,net} = (1-\alpha_{pl,b})(1+\alpha_a)\theta_{cw,on}+(1+\alpha_{pl,b})(1-\alpha_a)\theta_{cw,off} \qquad (22) </math>
 
−
 
 
−
in which <math>\alpha_{pl,b} = \alpha_{onshore} - \alpha_{offshore}</math> and,
 
−
 
 
−
 
 
−
<math>  \alpha_j = \Large \frac{\nu^{0.25} \ {U_{wj}}^{0.5}}{{W_s} \ {T_j}^{0.75}} \normalsize \exp\left[ - \left(\Large \frac{U_{w,crsf}}{U_{wj}} \right)^2 \normalsize \right] \qquad (23) </math>
 
−
 
 
−
where <math>U_{w,crsf}</math> is the critical velocity for inception of [[Definitions of coastal terms#Sheet flow|sheet-flow]] transport <ref name=”CL06”> </ref>}:
 
−
 
 
−
 
 
−
<math>  U_{w,crsf} = 8.35 \ [(s-1) g \ (d_{50} \ \delta_w)^{1/2}]^{1/2} \ (1 + r_w)  \qquad (24) </math>
 
−
 
 
−
where <math>\delta_w = \sqrt{\nu T_w / \pi}</math> is the Stokes boundary layer thickness <ref>Chan, K.W., Baird, M. H.I., Round, G.F., 1972. Behaviour of beds of dense particles in a horizontally oscillating liquid. Proc. Royal Society of London A(330), 537—559.</ref>, and <math>r_w</math> the wave asymmetry coefficient, <math>r_w = u_{w,max}/U_w-1 ,</math> with <math>u_{w,max}</math> being the maximum wave velocity.
 
−
 
 
−
Based on the work by Watanabe and Sato <ref name="WS"></ref>, the coefficient <math>\alpha_a</math> is given by <ref name="CL07"></ref> (see Fig. 3):
 
−
 
 
−
<math>  \alpha_a = \Large \frac{1-R_{ac}}{1+R_{ac}} \normalsize </math> with <math>R_{ac} = T_{ac}/T_{dc}  \qquad (25)</math>
 
−
 
 
−
 
 
−
 
 
−
==Suspended-load==
 
−
 
 
−
===Bijker (1971) formula===
 
−
 
 
−
Bijker <ref name="Bijk"></ref> related suspended load to bedload as the bed concentration reference value. Suspended load is then estimated using the Einstein integrals:
 
−
 
 
−
<math>  q_{ss} = 1.83 \ q_{sb} \ \left( I_1\ln \left[ \Large \frac{33 h}{\delta_c} \normalsize \right] +I_2 \right) , \qquad (26)  </math>
 
−
 
 
−
where <math>\delta_c=100d/h</math> is dimensionless thickness of the bed load layer.
 
−
 
 
−
The Einstein integrals  <math>I_1</math> and <math>I_2</math> for the suspended load are given:
 
−
 
 
−
<math>  I_1 = \Large \int_{\delta}^{1} (\frac{1-y}{y} )^A \normalsize dy , </math>
 
−
 
 
−
<math>  I_2 = \Large \int_{\delta}^{1} (\frac{1-y}{y} )^A \normalsize \ln y \ dy , \qquad (27) </math>
 
−
 
 
−
where <math>A=\Large \frac{W_s}{\kappa} \normalsize (\tau_{cw}/\rho)^{-1/2} </math> is a function determining the rate of the suspension, <math>\kappa=0.41</math> is the Von Karman constant, and  <math>W_s</math> the settling velocity.
 
−
 
 
−
 
 
−
===Bailard (1981) formula===
 
−
 
 
−
Following the work of Bailard and Inman <ref name="BI"></ref>, Bailard developed a total load formula, including a specific term for suspended load <ref name="Bail"></ref>:
 
−
 
 
−
<math>  \vec{q_{sb}} =  \Large \frac{0.5 \ f_{cw}}{g \ (s-1)} \normalsize \left( \Large \frac{\epsilon_s}{W_s} \normalsize <\mid\vec{u}\mid^3\vec{u}> \right)  \qquad (28) </math> 
 
−
 
−
where <math>\epsilon_s</math> is the suspended load efficiency, and <math>< \ ></math> yields an average over several periods of the wave.
 
−
 
 
−
The suspended load efficiency coefficient is also slightly different from the one given by Bagnold <ref name="Bag66"></ref>. Bailard suggested from a calibration with field data that <math>\epsilon_s = 0.02</math>.
 
−
 
 
−
 
 
−
 
 
−
===Van Rijn (1989) formula===
 
−
 
 
−
The Van Rijn formula <ref name="Rijn84b"></ref><ref name="Rijn89"></ref> for suspended load corresponds to a resolution of the equation of concentration over depth:
 
−
 
 
−
<math>  \Large \frac{dc}{dz} \normalsize = - \Large \frac{(1-c)^5 \ c \ W_s}{\epsilon_{scw}} \normalsize , \qquad (29)</math>
 
−
 
 
−
where <math>c(z)</math> is the mean volume concentration (time averaged) at height <math>z</math>, <math>(1-c)^5</math> corresponds to the decrease of the settling velocity due to high concentrations, and <math>\epsilon_{scw}</math> is the mixing coefficient in case of a wave-current interaction.
 
−
Then, integrating sediment fluxes over depth:
 
−
 
 
−
<math>  q_{ss} = \int^h_{z_a} \overline{u(z)} \ c(z) \ dz  \qquad (30)</math>
 
−
 
 
−
where <math>h</math> is the water depth, <math>z_a={\rm max}(k_{sct},k_{swt})</math> the reference level, <math>k_{sct},k_{swt}</math> total roughness values due to current and waves, respectively, and <math>\overline{u(z)}</math> is the mean velocity (time averaged) at height <math>z</math>.
 
−
 
 
−
The reference concentration is estimated at the level <math>z_a</math> based on the Van Rijn bedload formula <ref name="Rijn89"></ref>:
 
−
 
 
−
<math> c_a = 0.015 \ \Large \frac{d_{50}}{z_a} \normalsize \ d_{*}^{-0.3} \ (\tau_{cw} / \tau_{cr} \ -1 )^{1.5}  . \qquad (31) </math>
 
−
 
 
−
The sediment diffusion coefficient for a wave and current interaction is given by <ref name="Rijn84b"></ref><ref name="Rijn89"></ref> :
 
−
 
 
−
<math> \epsilon_{scw}(z) = [\epsilon_{sc}(z)^2+\epsilon_{sw}(z)^2]^{1/2} \qquad (32) </math>
 
−
 
 
−
with:
 
−
 
 
−
<math>  \epsilon_{sc}(z) =  \epsilon_{sc,max} = 0.25 \kappa \beta_s u_* h \;</math> if  <math> \; z > h/2</math> ,
 
−
 
 
−
<math> \epsilon_{sc}(z) =  \epsilon_{sc,max} \ \left[1-\left(1-2 \Large \frac{z}{h} \right)^2 \normalsize \right] \; </math> if  <math> \; z \leq h/2  \qquad (33)  </math>
 
−
 
 
−
where <math>\beta_s={\rm min}(1.5,1+2(W_s/u_*)^2)</math>, and <math>u_*=\sqrt{\tau_{cw}/\rho}</math> is the shear velocity, and
 
−
 
 
−
<math>  \epsilon_{sw}(z) =  \epsilon_{sw,b} = 0.004 \ a_{br} \ d_* \ \delta_s \ U_w \; </math> if <math> \; z \leq \delta_s  , </math>
 
−
 
 
−
<math> \epsilon_{sw}(z) =  \epsilon_{sw,max} = 0.035 \ a_{br} \ h \Large \frac{H_w}{T_w} \normalsize \; </math> if <math> \; z > h/2 , </math>
 
−
 
 
−
<math> \epsilon_{sw}(z) =    \epsilon_{sw,b}+(\epsilon_{sw,max}-\epsilon_{sw,b}) \ \Large \frac{z-\delta_s}{h/2-\delta_s} \normalsize \; </math> if <math> \; \delta_s < z \leq h/2 \qquad (34) </math>
 
−
 
 
−
with <math>\delta_s=0.3 h (H_w/h)^{0.5}</math> is the thickness of the boundary layer, and <math>a_{br}={\rm max}(3 H_w/h-0.8,1)</math>, a coefficient.
 
−
The estimation of the time-averaged velocity is based on the logarithmic velocity profile:
 
−
 
 
−
<math>  \overline{u(z)} = U_c \ \Large \frac{\log (30 \delta_w/k_a)}{\log(30 h/k_a)-1} \ \frac{\log(30z/k_{sc})}{\log(30\delta_w/k_{sc})-1} \; \normalsize </math> if <math> \; z \leq \delta_w , </math>
 
−
 
 
−
<math> \overline{u(z)} = U_c \ \Large \frac{\log(30z/k_a)}{\log(30h/k_a)-1} \normalsize \; </math> if <math> \;  z > \delta_w  \qquad (35) </math>
 
−
 
 
−
with <math>\delta_w = 0.072 A_w (A_w/k_{sw})^{-0.25}</math> the thickness of the wave boundary layer, <math>A_w=U_w T_w/(2\pi)</math> the wave half-excursion.
 
−
 
 
−
Van Rijn updated his suspended-load formula. He proposed a new simplified suspended-load transport formula for steady flow (with or without waves) <ref name="Rijn07b"> van Rijn, L.C., 2007. Unified view of sediment transport by currents and waves. II: Suspended transport. J. Hydraulic Eng. 133(6), 668—689.</ref>:
 
−
 
 
−
<math>  q_{sb} = 0.015 \ U_c \ \Large \frac{d_{50}}{d_*^{0.6}} \normalsize \ \Psi^{2.0} \qquad (36) </math>.
 
−
 
 
−
 
 
−
===Camenen and Larson (2008) formula===
 
−
 
 
−
In determining the suspended load <math>q_{ss}</math>, following the simplified approach by Madsen <ref>Madsen, O.S., 1993. Sediment transport outside the surf zone. unpublished technical report, Waterways Experiment Station, U. S. Army Corps of Engineer, Vicksburg, Mississippi, USA.</ref> and Madsen et al. <ref>Madsen, O.S., Tajima, Y., Ebersole, B.A., 2003. Longshore sediment transport: a realistic order-of-magnitude estimate. In: Proc. Coastal Sediments'03. ASCE, Clearwater Beach, Florida, USA, pp. 1--8, cDROM.</ref>, the vertical variation in the horizontal velocity was neglected and an exponential-law profile assumed for the sediment concentration. The suspended sediment load is written (components along the wave direction and perpendicular) <ref name="CL08"></ref>:
 
−
 
 
−
<math>  q_{ssw} = U_{cw,net} \ c_R \Large \frac{\epsilon}{W_s} \normalsize \left[ 1 - \exp \left( -\Large \frac{W_s h}{\epsilon} \normalsize \right)\right] , </math>
 
−
 
 
−
<math>  q_{ssn} = U_c \sin\varphi \ c_R \Large \frac{\epsilon}{W_s} \normalsize \left[ 1 - \exp \left( -\Large \frac{W_s h}{\epsilon} \normalsize \right)\right]  \qquad (37) </math>
 
−
 
 
−
where <math>h</math> is the water depth, <math>U_{cw,net}</math> is the net mean current after a wave period, <math>c_R</math> the reference concentration at the bottom, <math>W_s</math> the sediment fall speed, and <math>\epsilon</math> the sediment diffusivity. In solving the integral, the ratio <math>W_s h / \epsilon</math> may often be assumed large, implying that the exponential term is close to zero. However, the assumption that integrating to infinity or to <math>h</math> produces about the same result, may not be valid when strong mixing due to wave breaking is present.
 
−
 
 
−
The bed reference concentration is obtained from
 
−
 
 
−
<math>  c_R =  A_{cR} \ \theta_{cw,m} \ \exp \left( -4.5 \ \Large \frac{\theta_{cr}}{\theta_{cw}} \normalsize \right)
 
−
  \qquad (38) </math>
 
−
 
 
−
in which the coefficient <math>A_{cR}</math> is given by
 
−
 
 
−
<math>  A_{cR} = 1.5 \ 10^{-3} \exp (-0.2 d_*)  \qquad (39) </math>
 
−
 
 
−
where <math>d_*=\sqrt[3]{(s-1)g/\nu^2} \ d_{50}</math> is the dimensionless grain size.
 
−
 
 
−
The sediment diffusivity is related to the energy dissipation <ref> Battjes, J.A., Janssen, J. P. F.M., 1978. Energy loss and set-up due to breaking of random waves. In: Proc. 16th Int. Conf. Coastal Eng. ASCE, pp.569--587.</ref>,
 
−
 
 
−
<math>  \epsilon = h (D /\rho)^{1/3} \qquad (40) </math>
 
−
 
 
−
in which <math>D</math> is the total effective dissipation expressed as
 
−
 
 
−
<math>  D =  {k_b}^3 \ D_b + {k_c}^3 \ D_c + {k_w}^3 \ D_w  \qquad (41) </math>
 
−
 
 
−
where the energy dissipation from wave breaking (<math>D_b</math>) and from bottom friction due to current (<math>D_c</math>) and waves (<math>D_w</math>) were simply added, and <math>k_b</math>, <math>k_c</math> and <math>k_w</math> are coefficients. The coefficient <math>k_b</math> corresponds to an efficiency coefficient (<math>k_b=0.010</math>), whereas <math>k_c</math> and <math>k_w</math> are related to the Schmidt number. Assuming a parabolic profile for the vertical sediment diffusivity, its mean value over the depth (for a steady current or waves, respectively) may be written as follows:
 
−
 
 
−
<math> \epsilon_j = h (D_j / \rho)^{1/3} = k_j \ \kappa \ u_{*j} \ h
 
−
  \qquad (42) </math>
 
−
 
 
−
where <math>k_j</math> is a function of the Schmidt number <math>\sigma_j</math> or the ratio between the vertical eddy diffusivity of particles and the vertical eddy viscosity of water. <math>u_{*j}</math> is the shear velocity due to current or waves only, with subscript <math>j</math> taking on the values <math>c</math> (current) or <math>w</math> (waves), respectively. In case of a steady current, <math>k_c =\sigma_c/6 \kappa</math>  whereas for waves <math>k_w =\pi \sigma_w /3 \kappa</math>. The following expression was developed for the Schmidt number:
 
−
 
 
−
<math>  \sigma_j = A_1 + A_2 \ \sin^{2} \left( \Large \frac{\pi}{2} \frac{W_s}{u_{*j}} \right) \; \normalsize  </math> if <math> \;  W_s/u_{*j} \leq 1 ,  </math>
 
−
 
 
−
<math>  \sigma_j = 1 + (A_1+A_2-1) \ \sin^{2} \left( \Large \frac{\pi}{2} \frac{u_{*j}}{W_s} \right) \normalsize \; </math> if <math> \;  W_s/u_{*j} > 1  \qquad (43) </math>
 
−
 
 
−
 
 
−
where <math>j</math> is a subscript equal to <math>c</math> or <math>w</math>. <math>A_{c1}=0.4</math>,  <math>A_{c2}=3.5</math>,  <math>A_{w1}=0.15</math> and <math>A_{w2}=1.5</math>. Recent measurements in large rivers showed however that <math>\sigma_c</math> may be overestimated using Eq. 43 for large water depth <ref>Camenen, B., Le Coz, J., Dramais, G., Peteuil, C., Fretaud, T., Falgon, A., Dussouillez, P., Moore, S.A., 2014. A simple physically-based model for predicting sand transport dynamics in the Lower Mekong River. In: Schleiss, A.J., de Cesare, G., Franca, M.J., Pfister, M. (Eds.), River Flow, Proc. 7th Int. Conf. on Fluvial Hydraulics. Lausanne, Switzerland, pp. 2189--2197.</ref>. For wave-current interaction, a weighted value is employed for the Schmidt number:
 
−
 
 
−
<math>  \sigma_{cw}=X_t \ \sigma_c +(1-X_t) \ \sigma_w  \qquad (44) . </math>
 
−
 
 
−
The net mean current is defined in a similar way to the net Shields parameter for the bed load in order to take into account a possible sediment transport due to wave asymmetry, as well as a possible phase-lag effects on the suspended concentration,
 
−
 
 
−
<math>  U_{cw,net} = (1-\alpha_{pl,s})U_{cw,on}+(1+\alpha_{pl,s})U_{cw,off}  \qquad (45) </math>
 
−
 
 
−
where <math>\alpha_{pl,s}</math> is the coefficient describing phase-lag effects on the suspended load, and <math>U_{cw,j}</math> is the root-mean-square value of the velocity (wave+current) over the half period <math>T_{wj}</math>, where the subscript <math>j</math> should be replaced either by <math>on</math> (onshore) or <math>off</math> (offshore) (see also Fig. 1) according to:
 
−
 
 
−
 
 
−
<math>  U_{cw,on} =  [\Large \frac{1}{T_{wc}} \int_0^{T_{wc}} \normalsize (u_w(t)+U_c \cos\varphi)^2 dt  ]^{1/2},</math>
 
−
 
 
−
 
 
−
<math>  U_{cw,off} = [\Large \frac{1}{T_{wt}} \int_{T_{wc}}^{T_w} \normalsize (u_w(t)+U_c\cos\varphi)^2 dt]^{1/2}. \qquad (46) </math>
 
−
 
 
−
In case of a steady current <math>U_{cw,net}=U_c</math>.
 
  
 +
'''Flood deltas''' are sedimentary bodies deposited by flood currents. '''Ebb-tidal deltas''' are sedimentary bodies deposited by ebb currents. Flood deltas and ebb-tidal deltas are generally present at the inshore and offshore sides (respectively) of [[#Tidal inlet|tidal inlets]] of [[#Estuary|estuaries]] and [[#Lagoon|tidal lagoons]].   
 +
===Dispersion===
 +
#The passive dispersal of dissolved substances in the marine or estuarine environment. Dispersion is the overall mixing effect of all hydrodynamic processes including turbulence, flow circulations and gradients in current velocity. See: [[Seawater intrusion and mixing in estuaries]], [[Transport and dispersion of pollutants, nutrients, tracers in mixed nearshore water]], [[Shelf sea exchange with the ocean]].
 +
# Wave field transformation due to the dependence of propagation speed on wave frequency.
 +
===Dissipative and reflective beaches===
 +
Dissipative beaches have typically gentle coastal profiles; they are subjected to energetic short-crested [[#Wave|waves]], which are strongly damped in the nearshore zone. Dissipative beaches have medium to large [[#Intertidal zone|intertidal zones]] which consist of fine (sandy or muddy) sediment. Reflective beaches have typically steep slopes and are subjected to low-energy [[#Wave|swell waves]]. An intertidal zone is almost absent and the beach consists mainly of coarse (sandy or gravelly) sediment. Beach types can be characterised by the so-called ' Dean parameter ' <math>\Omega=H_0/(w_s T_p)</math>, where <math>H_0</math> is the deep-water [[#Wave height|wave height]], <math>w_s</math> the mean fall velocity of beach sediment and <math>T_p</math> the peak spectral wave period. Reflective beaches correspond to  <math>\Omega < 1</math> and dissipative beaches to <math>\Omega > 6</math>. See [[Characteristics of sedimentary shores]].
 +
===Dunes===
 +
#The term 'dunes' generally indicates subaerial dunes. These dunes are ridges or moulds of loose, wind-blown sand (fine to medium) forming on the [[#Backshore|backshore]] and forming the coastal features at certain locations. Dunes are more or less vegetated. Dunes are active coastal form elements acting as a flexible sand reservoir. At coasts subject to [[#Coastal erosion|structural coastal erosion]] they are moving backwards in parallel with shoreline retreat. Dunes act as a kind of flexible natural protection against erosion and flooding, see [[Dune erosion]]. If the vegetation is damaged by too much traffic or grazing etc. the integrity of the dunes may be endangered.
 +
#The term 'dunes' is also used for subaqueous dunes, which are frequently called '''sandwaves'''. Subaqueous dunes are [[#Bed forms|bed forms]] induced by the interaction of the seabed with currents. Sandy seabeds are often covered with dune fields in regions where the maximum (tidal) current velocity is in the range 0.5-1.5 m/s. Dune spacing (generally more than 10 m and less than 1000 m) depends mainly on water depth. Dunes can reach a height of 10-50% of the water depth; high dunes present a risk for navigation.
 +
===Environmental impact assessment (EIA)===
 +
A written analysis of the predicted environmental consequences of a proposed development activity, including
 +
*a description of the avoidable and unavoidable adverse environmental effects (in conjunction with the cumulative effect of other human interventions);
 +
*a description of alternatives to the activity which might be less harmful to the environment, together with the reasons why such alternatives were rejected;
 +
*a description of any required irreversible or irretrievable commitments of resources required by the proposed development activity.
 +
===Estuary===
 +
The transition zone between the riverine and the marine environment. A usual definition is: a semi-enclosed coastal body of water, which has a free connection with the open sea, and within which sea water is measurably diluted with freshwater derived from land drainage. Strong tides intrude in general much further upstream than seawater. From a morphological and sedimentary point of view it is therefore more logical to consider as upstream estuarine boundary the location where tidal discharges become much smaller than river discharges, instead of the seawater intrusion limit. See: [[Seawater intrusion and mixing in estuaries]], [[Morphology of estuaries]].
 +
===Estuarine circulation===
 +
Residual flow pattern in an estuary driven by density differences between fluvial water and seawater.
 +
See: [[Estuarine circulation]], [[Salt wedge estuaries]].
 +
===Excavation===
 +
See [[#Mining|Mining]] 
 +
===Fetch===
 +
Length in the wind direction of the marine area where water waves are generated by wind.
 +
===Friction===
 +
Shear stresses generated by the seabed and by flow obstacles, causing loss of fluid momentum. The shear stresses are transmitted to the flow via the turbulent [[#Boundary layer|boundary layer]]. See: [[#Bed forms|Bed forms]], [[Bed roughness and friction factors in estuaries]], [[Bedforms and roughness]]
 +
===Foreshore===
 +
Foreshore or ('''beach face''') is the zone between mean low water (MLW) and the seaward [[#Beach berm|beach berm]], which is equivalent to the upper limit of [[#Wave run-up|wave run-up]] at high tide, see Fig. 1. The foreshore is the part of the [[#Beach|shore/beach]] which is wet due to the varying tide and wave run-up under normal conditions, i.e., excluding the impact of extreme storm waves and [[#Storm surge|storm surge]]. This means that the foreshore in morphological terms extends further up on the beach than the intersection between the mean high water (MHW) and the coastal profile (MHW line). However, for practical reasons the administrative upper delineation of the foreshore is often defined as the intersection between the MHW line and the coastal profile, which is identical to the definition of the [[#Shoreline|shoreline]].
 +
===Graded sediment===
 +
A sediment bed composed of a mixture of fine and coarse grained sediment particles. 
 +
===Gravel beach===
 +
Beach built of granular material with a size larger than 1 mm:  very coarse sand (>1 mm), gravel (2-4 mm), pebbles (4-64 mm) and cobbles (>64 mm), see [[Coastal and marine sediments]]. Beach material often originates from erosion of nearby cliffs or is supplied by gravel rivers draining nearby mountains. Gravel beaches have steep slopes and occur on coasts exposed to strong wave action. [[#Beach cusps|Cusp patterns]] are a common beach feature. See: [[Gravel Beaches]].
 +
===Groyne or groin===
 +
A straight structure perpendicular to the shoreline. Groynes work by blocking (part of) the [[#Littoral drift|littoral drift]]. They trap/maintain sand on their updrift side and cause erosion on the downdrift side. Groynes can have special shapes and they can be emerged, sloping or submerged, they can be single or in groups, the so-called groyne fields. Groynes are normally built as rubble mound structures, but they can also be constructed in other materials, such as concrete units, timber, etc. See: [[Groynes]], [[Groynes as shore protection]], [[Deteriorated groynes]].
 +
===Headland===
 +
Land mass with a considerable elevation that borders beaches. Headlands form the boundaries to [[#Sediment cell|sediment cells]], compartmentalising sand transport along the shore, and reducing sand exchange between adjacent beaches.
  
 +
Artificial headlands are smooth structures built from the coastline over the beach and some distance out on the shoreface. They work by blocking (part of) the littoral transport. A headland combines the effects of groynes and detached breakwaters and at the same time, minimises some of the disadvantages of groynes and breakwaters – see [[Detached breakwaters#Modified breakwaters and headlands| Modified breakwaters and headlands]].
 +
===Infragravity waves===
 +
Ocean surface waves with a period of typicallly 25-250 s. They arise in particular through non-linear interactions within [[#Wave group|wave groups]]. They play an important role in beach dynamics of [[#Dissipative and reflective beaches|dissipative coasts]] because their amplitude increases shoreward, relative to the breaking short waves. See: [[Infragravity waves]].
 +
===Internal waves===
 +
Waves on the [[#Stratification|interface]] of fluid layers with different densities. Internal waves can be very large when the density difference between the fluid layers is small. Breaking of internal waves contributes to mixing of the layers and destruction of the layer structure.
 +
===Intertidal zone===
 +
Area which is dry at low water (LW) and submerged at high water (HW), where LW and HW refer to mean [[#Tidal range|spring tide]]. The [[#Foreshore|foreshore]], [[#Tidal flat|tidal flats]] and (parts of) [[#Salt marsh|salt marshes]] are intertidal zones. 
 +
===Jetty===
 +
#Breakwater protecting a harbour entrance channel from wave action (also called '''harbour mole''');
 +
#Structure (often a bridge) connecting an offshore ship mooring to the coast. 
 +
===Lagoon===
 +
Area of relatively shallow water situated in a coastal environment, separated from the open marine conditions by a natural barrier (a [[#sand spit|sand spit]], a barrier island or a coral reef), but with an access to the sea. One may distinguish between microtidal and macrotidal lagoons. Examples of microtidal lagoons are Great South Bay and Pamlico Sound at the US Atlantic coast. Examples of macrotidal lagoons (also called '''tidal lagoons''') are the Wadden Sea at the Dutch-German-Danish North Sea coast and the Bassin d'Arcachon at the French Atlantic coast. Tidal lagoons are distinct from microtidal lagoons by the existence of deep [[#Tidal inlet|tidal inlets]] and large [[#Tidal flat|tidal flats]]. See also: [[Morphology of estuaries]].
 +
===Littoral cell===
 +
See [[#Sediment cell|Sediment cell]]
 +
===Littoral drift===
 +
Littoral drift or '''longshore sediment transport''' is the term used for the longshore transport of non-cohesive sediments, i.e. mainly sand, along the [[#Foreshore or Beach face|foreshore]] and the [[#Shoreface|shoreface]] due to the action of breaking [[#Wave|waves]]  and [[#Longshore current|longshore current]]. The littoral dift is also called longshore sediment transport. Formulas for the longshore sediment transport are given in: [[Littoral drift and shoreline modelling]]; see also [[Coastal Hydrodynamics And Transport Processes]].
 +
===Littoral zone===
 +
See [[#Shoreface|Shoreface]]
 +
===Longshore current===
 +
The longshore current or nearshore current is the dominating current in the [[#Nearshore zone|nearshore zone]] and is running parallel to the shore. The longshore current is generated by the shore-parallel component of the stresses associated with the breaking process for obliquely incoming [[#Wave|waves]] , the so-called radiation stresses, and by the surplus water which is carried across the [[#Breaker zone|breaker zone]] towards the coastline. See: [[Shallow-water wave theory]].
 +
===Longshore sediment transport===
 +
See [[#Littoral drift|Littoral drift]]
 +
===Management unit (MU)===
 +
A management unit is a coastal stretch with coherent characteristics in terms of both natural coastal processes and land use. The MU is used as boundary for Shoreline Master Plans.
 +
===Marine regression===
 +
Coastal extension due to a falling relative sea level.
 +
===Meandering===
 +
Natural propensity of a flow to scour the outer bend of a channel. When a channel meander becomes very large a cutoff channel (a so-called '''channel chute''') is often formed, leading to [[#Avulsion|avulsion]] of the meander.
 +
===Mining===
 +
Mining (or '''excavation''') is the mechanical removal of consolidated soil or unconsolidated material (aggregates like sand, gravel, shells) from seabed, beach or dunes. 
 +
===Mitigation===
 +
Action (or series of actions) aimed at (partly) neutralising the adverse impacts of past or planned human interventions.
 +
===Model===
 +
Physical or mathematical representation of nature, for studying or predicting coastal behaviour; see [[Modelling coastal hydrodynamics]].
 +
* Physical models. These models copy salient features of nature at a reduced scale in a laboratory setting. Scale effects are an important issue for the translation of observed model results to the natural scale. Major scale effects generally arise for the representation of phenomena influenced by [[#Friction|friction]], by [[#Sediment transport|sediment transport]] (including sediment erosion and deposition) and by biota.
 +
* Mathematical models. These models solve in one way or another the governing hydrodynamic (and/or morphodynamic) equations . They exist in many different types, see for example [[Estuarine morphological modelling]].  Most common types are: Analytical models, Numerical process-based models, Behaviour-based models, Stochastic models, Data-driven models, Particle-based models and Cellular models. '''Analytical models''' are based on explicit solutions of the governing equations, which are strongly simplified to retain only those features which are most pertinent to the studied phenomena. '''Numerical process-based''' models describe nature on a discretised grid, retaining all physical features relevant for a reliable and accurate representation of the studied phenomena; the governing equations are solved numerically for successive discrete time steps, see [[Process-based modelling]], [[Process-based morphological models]]. '''Behaviour-based models''' (also called Aggregate-scale models) consider the coastal system as an assembly of interacting subsystems and solve the governing equations numerically for the interactions at system level, whereas empirical relationships are used for representing the dynamics at subscale levels; see: [[Behaviour-based models]]. '''Stochastic models''' are process-based models which use probability distributions for certain input data for taking into account natural fluctuations (wave climate, river discharge, for example) or uncertainty (sea-level projections, model parameters, for example); see [[Stochastic and fractal methods in coastal morphodynamics]]. '''Data-driven models''' are used to make moving forecasts by integrating observed data of the recent history to calibrate uncertain model parameters or uncertain model input data, see: [[Reduction of uncertainties through Data Model Integration (DMI)]]. '''Particle-based models''' describe numerically the motion of discrete fluid parcels taking into account their mutual interaction according to the laws of physics; in the most popular method (called '''Smoothed-particle Hydrodynamics (SPH)''') the fluid is divided into a set of discrete moving parcels with properties which are smoothed over the parcel size according to a prescribed smoothing function. '''Cellular models''' divide the coastal system in fixed discrete cells which behave in a prescribed way according to the evolution of neighbouring cells, taking into account physical conservation laws.
 +
*Hybrid models combine physical and numerical models.
 +
===Morphology===
 +
Morphology is the study of the form of things. In the coastal context, morphology or geomorphology is generally used for designating the coastal [[#bathymetry|bathymetry]], including its sedimentary composition and structure. See also [[#Coastal morphology|Coastal morphology]].
 +
===Morphodynamics===
 +
See [[#Coastal morphology|Coastal morphology]]. 
 +
===Mud===
 +
Fine cohesive [[#Sediment|sediment]] deposit containing a high fraction (≥20%) of clay minerals. Fine  sedimentary particles, consisting of clay minerals, but also other particles (silt, fine sand, organic matter), can be glued together by large organic molecules (extracellular polymeric substances, EPS) into large mud flocs. These flocs, with a diameter of  0.1-1 mm, settle much faster than the individual particles and can form a colloidal suspension on the seabed. This so-called '''fluid mud layer''' can move along the seabed (driven by pressure gradients at the interface, by flow entrainment or by bed slope effect) and be a major cause of harbor [[#Siltation|siltation]]. After consolidation, which is often a lengthy process, a mud bed can become highly resistant to erosion by currents. See: [[Dynamics of mud transport ]], [[Sediment deposition and erosion processes]], [[Characteristics of muddy coasts]]. 
 +
===Nearshore zone===
 +
The zone extending seaward from the low water line well beyond the [[#Breaker zone|breaker zone]]; it defines the area influenced by the nearshore currents. The nearshore zone extends somewhat further seaward than the [[#Shoreface|littoral zone]].
 +
===Nourishment===
 +
Nourishment (or '''sand nourishment''') is a method to neutralize the effect of coastal erosion by maintaining the sand volume of the [[#Active coastal zone|active coastal zone]]. Sand is extracted (generally by dredging) from nearby sources and applied to the beach, the [[#Shoreface|shoreface]] or the dunes. The costs highly depend on the location of available sand sources, which should be situated outside (seaward of) the [[#Active coastal zone|active coastal zone]]. Dune nourishment is usually meant for safety against flooding, beach nourishment for restoration of the beach and shoreface nourishment for stabilizing the shoreline. See:  [[Shore nourishment]], [[Artificial nourishment]].
 +
===Overwash===
 +
Wave uprush over a natural or artificial coastal barrier. The term overwash is also used for the resulting sand deposit at the leeside of the barrier. 
 +
===Offshore zone===
 +
The offshore zone is not clearly delimited. In relation to beach terminology, the offshore zone is often defined as the zone off the [[#Nearshore zone|nearshore zone]].
 +
===Progradation===
 +
Coastal extension into the sea due to natural [[#Accretion or Aggradation|aggradation]]. Coastal progradation occurs specifically where rivers supply large amounts of sediment.
 +
===Propagation speed===
 +
The speed at which a [[#Wave|wave]] propagates. The speed <math>c</math> of a wave propagating without frictional losses in shallow water is proportional to the square root of the water depth <math>h</math>  (formula: <math>c=\sqrt{gh}</math>). A [[#Wave group|wave group]] propagates at a smaller speed <math>c_g</math> than the constituent short waves. [[#Wave energy|Wave energy]] propagates at the speed of the wave group. See: [[Shallow-water wave theory]].
 +
===Reclamation===
 +
The transformation of areas which were formerly part of the marine or estuarine domain into non-floodable land.
 +
===Reef===
 +
A ridge of material at or near the surface of the ocean. Natural reefs are made of rocks or the skeletons of small animals called corals. Reefs can also be created artificially for several reasons:
 +
* Protect coastlines from erosion;
 +
* Promote sea life for recreation and aquaculture;
 +
* Create a wave pattern that promotes the sport of surfing.
 +
See: [[Natural barriers]], [[Artificial reefs]].
 +
===Reflective beaches===
 +
See [[#Dissipative and reflective beaches|Dissipative and reflective beaches]]
 +
===Refraction===
 +
The propensity of [[#Wave|waves]]  to align the wave front in shallow water with the depth contour, according to Snell's law. Also: Change of wave propagation direction due to the interaction with currents.
 +
===Rip current===
 +
A local current directed away from the shore, bringing the surplus water carried over [[#Breaker bar|breaker bars]] back into deeper water. Rip currents may occur at certain intervals along the shoreline as a result of the interaction between breaking [[#Wave|waves]]  and the nearshore bathymetry, see: [[Rhythmic shoreline features]], [[Stability models]]. The rip opening in the [[#Breaker bar|breaker bars]] will often form the lowest section of the coastal profile; a local setback in the shoreline is often seen opposite the rip opening. The rip opening travels slowly downstream. Rip currents are dangerous for swimmers.
 +
===Revetment===
 +
A revetment is a facing of stone, concrete units or slabs, etc., built to protect a scarp, the foot of a cliff or a dune, a dike or a seawall against erosion by wave action, storm surge and currents. This definition is very similar to the definition of a seawall, however a revetment does not protect against flooding. Furthermore, a revetment is often a supplement to other types of protection such as seawalls and dikes. See [[Revetments]], [[Seawalls and revetments]].
 +
===Runnel===
 +
Small beach channel draining a tidal pool left on the beach after high water.
 +
===Salt marsh===
 +
A densely vegetated coastal ecosystem situated in the upper coastal [[#Intertidal zone|intertidal zone]] between land and [[#Tidal flat|intertidal mudflats]], or bordering directly open saltwater or brackish water if mudflats are absent. Salt marshes are sometimes referred to as '''schorre''' or '''kwelder'''. The soil may be composed of deep mud and peat. Salt marshes usually form in areas that are well sheltered, such as [[#Lagoon|lagoons]] and [[#Estuary|estuaries]] where fine sediments can be deposited. They also form behind spits and artificial sea defences where tidal waters can flow gently and deposit fine sediments. See also: [[Salt marshes]].
 +
===Sand bank===
 +
Popular term for large [[#Bar|bars]] and [[#Tidal ridge|ridges]] in tidal waters, especially in relation to navigation hindrance.
 +
===Sand nourishment===
 +
See [[#Nourishment|Nourishment]]
 +
===Sand spit===
 +
See [[#Spit|Spit]]
 +
===Sand wave===
 +
# A subaqueous [[#Dunes|dune]];
 +
# A shoreline undulation with a wavelength in the range of a few hundred meters to a few kilometers, see: [[Rhythmic shoreline features]].
 +
===Sea-level rise===
 +
The so-called greenhouse effect or global warming causes a rise of the mean sea level, which will have a great impact on long-term coastal morphology, see [[Sea level rise]]. The long-term gradual sea-level rise will cause a general [[#Coastline retreat|coastline retreat]] and an increased flooding risk depending on local conditions. Instead of the absolute rise of the mean sea level it is more relevant to consider the '''relative sea-level rise''': the rise relative to vertical land motions that can be positive ('''uplift''') or negative ('''subsidence'''). An estimate of coastline retreat due to relative sea-level rise can be derived from the so-called '''Bruun rule''', which is valid under certain rather restrictive conditions, see: [[Bruun rule]].
 +
===Sediment===
 +
Fine-grained loose particles such as gravel, sand, mud. These sediments are produced by chemical or physical weathering of rocks, by seabed erosion and by soil erosion in river basins. They are called clastic sediments and consist of quartz, feldspar, mica and clay minerals. Other particles have a biotic origin, for example shell debris, peat, detritus, fecal pellets and plankton. Sediment particles have widely different grainsizes:  clay (< 0.002 mm), silt  (0.01-0.02 mm), sand (0.1-2 mm), gravel (2-5 mm). The density is of the order of 2.65 times the density of water. Sand or gravel beds occur in zones with strong (tidal) currents and strong wave activity, whereas fine sand, silt and mud cover the seabed in sheltered zones where currents and wave activity are weak. See: [[Coastal and marine sediments]], [[Sediment deposition and erosion processes]], [[Gravel Beaches]].
 +
===Sediment cell===
 +
A sediment cell (or '''littoral cell''' or '''coastal cell''') is a coastal compartment that contains a closed cycle of sedimentation including sources, transport paths, and sinks. The cell boundaries (often corresponding to headlands or jetties) delineate the geographical area within which the budget of sediment is balanced, providing the framework for the quantitative analysis of coastal erosion and accretion.
 +
===Sediment transport===
 +
The capacity of currents and [[#Wave|waves]]  to move [[#Sediment|sediments]]. Sediment transport is a crucial link in the interaction between coastal morphological evolution and waves, currents and tides. Sedimentation is related to convergence of sediment transport and erosion to divergence of sediment transport. Sediment transport takes place in several ways: Suspended-load transport, Bedload transport and Fluid mud motion. '''Suspended-load transport''' is the transport of sedimentary particles that are suspended in the fluid. '''Bedload transport''' is the transport of sedimentary particles that are rolling or leaping along the seabed. '''Fluid mud transport''' is the motion of a [[#Mud|fluid mud layer]] along the seabed. Formulas for bedload transport are based on empirical relationships involving characteristics of sediment, currents and waves. See: [[Sediment transport formulas for the coastal environment]], [[Sand transport]]. 
 +
===Seiche===
 +
Oscillation of a semi-enclosed water body caused by incoming long-period waves (periods typically in the range 200-2000 s). Seiches can be strongly amplified in harbour basins if the period is close to the harbour resonance period, causing damage to ships and moorings.
 +
===Setback area===
 +
A strip along the coastal zone where certain development activities are prohibited or significantly restricted. See: [[Setback area]].
 +
===Sheet-flow===
 +
Sheet-flow sediment transport refers to transport of sandy sediments as a fluidized thin surface layer (thickness of ten to several tens grain diameters). This type of sediment transport occurs under strong wave action (wave orbital velocity greater than 1 m/s), where bed ripples are flattened out. In the sheet-flow layer, continuous contacts between sand grains create an intergranular stress. This stress decreases the velocity in the sheet-flow layer to about one half the velocity in the top layer. The sediment concentration in the sheet-flow layer is in the order of 100 to 1000 kg/m3. See: [[Sediment transport formulas for the coastal environment]].
 +
===Shelf sea===
 +
See [[#Continental shelf|Continental shelf]].
 +
===Shoaling===
 +
Amplification of incident [[#Wave|waves]]  in the [[#Nearshore zone|nearshore zone]] before breaking. Amplification is due to (approximate) continuity of the '''wave energy flux''' <math>F=c_g E</math> seaward of the [[#Breaker zone|breaker zone]], where <math>E</math> is the [[#Wave energy|wave energy]]  and <math>c_g</math> the [[#Wave group|wave group]] [[#Propagation speed|propagation speed]]. The landward decrease of <math>c_g</math> results in a landward increase of <math>E</math>, thus in a landward increase of [[#Wave height|wave height]] <math>H</math>. See: [[Shallow-water wave theory]].
 +
===Shore protection===
 +
See [[#Coastal protection|Coastal protection]].
 +
===Shoreface===
 +
The shoreface (or '''littoral zone''') is part of the [[#Active coastal zone|active coastal zone]], situated seaward of the low water line. This zone extends seaward from the [[#Foreshore or Beach face|foreshore]] to some distance beyond the [[#Breaker zone|breaker zone]]. The littoral zone is the zone in which littoral morphodynamic processes take place, related mainly to [[#Littoral drift|longshore sediment transport]] and cross-shore sediment transport. The width of the instantaneous littoral zone varies dependent of the wave conditions. In the general context, the littoral zone is defined as the zone corresponding to the yearly wave climate. The width of the littoral zone can thus be defined as the width of the sediment transport zone for the significant [[#Wave height|wave height]], which is exceeded 12 hours per year, <math>H_{s,12h/y}</math>.
 +
===Shoreline===
 +
The intersection between the mean high water line and the shore. The line delineating the shoreline on Nautical Charts (Sea Maps) approximates this Mean High Water Line. The shoreline is not easy to identify in the nature in contrast to the coastline, which is based on a clear morphological shift between the shore and the coast.
 +
===Shoreline management===
 +
The act of dealing – in a planned way – with actual and potential coastal erosion and its relation to planned or existing development activities on the coast, see [[Shoreline management]]. The objectives of Shoreline Management are:
 +
*To ensure the development activities in the coastal area follow an overall land use plan and a general environmental policy;
 +
*To ensure the development activities in the coastal area do not cause to or aggravate erosion;
 +
*To ensure that development activities do not occur in sensitive areas;
 +
*To ensure that erosion control techniques are cost-effective and socially and environmentally acceptable.
 +
Shoreline management is typically based on [[#Sediment cell|coastal sediment cells]].
 +
===Siltation===
 +
Accumulation of fine sediments (sand, silt, mud) in channels, harbors and fairways. See: [[Siltation in harbors and fairways]], [[Dynamics of mud transport ]], [[Sediment deposition and erosion processes]], [[Sediment transport formulas for the coastal environment]].
 +
===Slack tide===
 +
Tidal phase at which the current turns from flood to ebb (high-water slack tide) or from ebb to flood (low-water slack tide).
 +
===Shore===
 +
See [[#Beach|Beach]]
 +
===Spit===
 +
A spit (or '''sand spit''') is an accretionary feature formed by [[#Littoral drift|littoral drift]], consisting of a long narrow accumulation of sand or gravel, lying generally in line with the coast, with one end attached to the land and the other projecting into the sea or across the mouth of an [[#Estuary|estuary]] or [[#Lagoon|lagoon]]. During dry periods, a spit can develop into a '''barrier''' that temporarily blocks the mouth of a lagoon or a small river.
 +
===Storm surge===
 +
The rise in water-level on an open coast as a result of the combined impact of the wind stress on the water surface, the atmospheric pressure reduction and local topographic features. The storm surge does not include the effect of the astronomical tide. The storm at a location is in first approximation inversely proportional with the water depth in the [[#Offshore zone|offshore zone]]. This implies that shores out to deep oceans will only be exposed to relatively small surges whereas shores out to shallow seas can be exposed to high surges. See: [[Extreme storms]].
 +
===Stratification===
 +
Less dense water layer overlying a water layer of higher density (related to higher salinity, lower temperature or higher suspended sediment concentration).  Density differences in the vertical inhibit turbulent mixing, which causes the interface of the layer to be sharpened. See: [[Salt wedge estuaries]].
 +
===Subsidence===
 +
Downward motion of the land surface. It is most often related to soil compaction (underground material movement) caused by the removal of water, oil, natural gas, or mineral resources out of the ground by drainage, pumping, fracking, or mining activities. Subsidence can also be caused by natural events such as earthquakes, glacial isostatic adjustment, erosion, sinkhole formation, sediment loading by river deposites, and adding water to fine soils deposited by wind (a natural process known as loess deposits).
 +
===Surf beat===
 +
Oscillation of the [[#Wave set-up|wave set-up]] on the foreshore. The oscillation is related to the breaking of [[#Wave group|wave groups]] in the [[#Breaker zone|surf zone]]. See: [[Shallow-water wave theory]].
 +
===Surf zone===
 +
See [[#Breaker zone|Breaker zone]].
 +
===Swash===
 +
Wave propagation on the beach, consisting of a decelerating onshore phase (swash or '''uprush''') and an accelerating offshore phase (backwash or '''downrush'''). On [[#Dissipative and reflective beaches|dissipative coasts]] swash processes are dominated by [[#Infragravity waves|infragravity waves]]. See: [[Swash zone dynamics]].
 +
===Swash bar===
 +
See [[#Beach berm|Beach berm]]
 +
===Tidal bore===
 +
Breaking [[#Tidal wave|tidal flood wave]]. Tidal bores occur in shallow funnel-shaped [[#Estuary|estuaries]] with a large tidal range (generally more than 6 m). 
 +
===Tidal channel===
 +
Seabed incision concentrating the main tidal flow. Tidal channels form naturally in sedimentary environments where tide-induced water motion is stronger than wave-induced water motion. 
 +
===Tidal creek===
 +
Drainage channel of a [[#Salt marsh|salt marsh]].
 +
===Tidal flat===
 +
Shallow, sandy or muddy part of the [[#Foreshore or Beach face|foreshore]], which is covered and uncovered by the rise and fall of the tide. Muddy tidal flats are also called '''mud flats''' or '''slikke'''. As a rule of thumb, a tidal flat normally develops when the relative tidal range RTR, defined as the ratio between the mean spring tidal range and the annual average [[#Wave|significant wave height]] <math>H_s</math>, is higher than 15.
 +
===Tidal inlet===
 +
The entrance to estuaries on sandy shores that have formed where sand barriers or spits enclose bays. They comprise a [[#Delta|flood and ebb tidal delta]], and a deep narrow throat through which strong currents flow.
 +
===Tidal prism===
 +
Volume of water flowing during flood through a [[#Tidal inlet|tidal inlet]], or through a certain section of an [[#Estuary|estuary]] or a [[#Lagoon|tidal lagoon]].
 +
===Tidal range===
 +
Water level difference between high water and low water, i.e. twice the '''tidal amplitude'''. The tidal range changes from tide to tide depending on the positions of moon and sun relative to the earth; the most important change is the fortnightly variation from '''spring tide''' to '''neap tide'''.
 +
===Tidal ridge===
 +
Sand ridge with a length of several tens of kilometers and height of a few tens of meters, produced by tidal currents on a [[#Continental shelf|shelf sea]]. Sand ridge fields consist of a number of tidal ridges with a spacing of the order of 5 km. See: [[Sand ridges in shelf seas]].
 +
===Tidal wave===
 +
The wave associated with tidal motion. The term "tidal wave" is also frequently used as a popular expression for an unusually high and destructive water level along a shore, thus including the combined effect of astronomical and meteorological surges.
 +
===Tide===
 +
The tide (more precisely, the '''astronomical tide''') is generated by the rotation of the earth in combination with the varying gravitational impact on the ocean of the sun, the moon and the planets. These phenomena cause predictable and regular oscillations in the water level, which is referred to as the tide. The astronomical tide at a specific location can be predicted and is published in Tidal Tables. See: [[Ocean and shelf tides]], [[Tidal motion in shelf seas]]. The term 'tide' is sometimes used for the combined effect of astronomical tide and wind-driven set-up or set-down of the sea level (including [[#Storm surge|storm surges]]). 
 +
===Transgression===
 +
Flooding of land by the sea related to relative [[#Sea-level rise|sea-level rise]]. Transgression implies [[#Coastline retreat|coastline retreat]].
 +
===Tsunami===
 +
Wave (or group of waves) generated by a subsea earthquake. Tsunamis propagate very fast over the ocean with very few energy loss due to the great ocean depth (see: [[#Propagation speed|propagation speed]]). In nearshore waters the amplitude increases dramatically (up to a factor 10) due to [[#Shoaling|shoaling]]. 
 +
===Turbidity maximum===
 +
Convergence zone of suspended sediment transport in an [[#Estuary|estuary]], where turbidity levels are high due to high suspended sediment concentrations. Upstream (landward) transport of fine suspended sediment in an estuary is possible due to [[#Estuarine circulation|estuarine circulation]] and tidal asymmetry (maximum flood current stronger than maximum ebb current). This produces a maximum in the suspended sediment concentration just downstream of the zone where the influence of river discharge on sediment transport becomes dominant. Fine sediments in the turbidity maximum zone settle to the bed in periods where currents are small (slack tide, neap tide), which may result in the formation of [[#Mud|fluid mud layers]]. High turbidity often causes oxygen depletion and mortality of estuarine organisms. It also enhances sedimentation of [[Tidal flat|tidal flats]] and harbours. See: [[Dynamics of mud transport]].
 +
===Turbulence===
 +
Irregular flow pattern of individual fluid parcels related to small-scale flow instability, see [[#Boundary layer|Turbulent boundary layer]]. Turbulence plays a major role in mixing processes and in energy dissipation. See: [[Transport and dispersion of pollutants, nutrients, tracers in mixed nearshore water]], [[Currents and turbulence by acoustic methods]].
 +
===Wave===
 +
The term "wave" designates in most cases surface water waves generated by wind (other types of waves are explicitly referred to as [[#Tidal wave|tidal wave]], [[#Tsunami|tsunami]] wave, etc.). A wave field is generally a superposition of waves of different height, period and direction that can be described by a '''wave spectrum'''. A unidirectional wave field is often characterised by the '''significant wave height''' <math>H_s</math> (representing approximately the mean [[#Wave height|wave height]] of the highest third of the waves) and the '''spectral peak period''' <math>T_p</math> (wave period with the highest energy).  See: [[Statistical description of wave parameters]]. Coasts situated on the open ocean are mainly subjected to long-period '''swell waves''', which are generated far away at the ocean and propagate to the coast with minor energy losses. Coasts situated on inland seas are mainly subjected to locally generated short-crested waves, also called "sea", see [[Waves]].
 +
===Wave breaking===
 +
Waves start breaking (by spilling or plunging) when entering shallow water, where the depth is smaller than one or two times the [[#Wave height|wave height]]. Waves may reform in the [[#Breaker zone|surf zone]], but remain depth-limited by spilling or by plunging a second time, until final collapse and [[#Swash|uprush]] on the beach. See: [[Shallow-water wave theory]].
 +
===Wave energy===
 +
Energy carried by waves when [[#Propagation speed|propagating]]. The wave energy <math>E</math> is proportional to the square of the [[#Wave height|wave height]] <math>H</math>  (formula: <math>E=g \rho H^2 / 8</math>).
 +
===Wave group===
 +
Incident waves generally arrive in groups, corresponding to the superposition of short-wave trains with slightly differing wave lengths and frequencies. Wave groups generate [[#Infragravity wave|infragravity waves]] with the same group wavelength and period, by non-linear interaction. Wave groups also cause [[#Surf beat|surf beat]]. See: [[Shallow-water wave theory]], [[Infragravity waves]].
 +
===Wave height===
 +
The water level difference between wave trough and wave crest, or twice the wave amplitude.
 +
===Wave run-up===
 +
The sum of [[#Swash|swash]] and [[#Wave set-up|wave set-up]]. Wave run-up is an important factor in the design of coastal protection structures and is a dominant process leading to the erosion of coastal dunes.
 +
===Wave set-up===
 +
Water level elevation at the foreshore related to wave breaking in the surf zone. Wave set-up is proportional to the [[#Wave height|wave height]] at the breaker line. As a rule of thumb, wave set-up is of the order of 20% of the offshore significant wave height. See: [[Shallow-water wave theory]].
 +
  
 
==Related articles==
 
==Related articles==
  
−
[[Definitions, processes and models in morphology]]
+
[[Coastal hydrodynamic and morphodynamic processes and engineering]]
−
 
 
−
[[Manual Sediment Transport Measurements in Rivers, Estuaries and Coastal Seas]]
 
−
 
 
−
[[Coastal Hydrodynamics And Transport Processes]]
 
−
 
 
−
[[Process-based morphological models]]
 
−
 
 
−
[[Littoral drift and shoreline modelling]]
 
−
 
 
−
[[Sand transport]]
 
−
 
 
−
[[Shallow-water wave theory]]
 
−
 
 
−
[[Coastal and marine sediments]]
 
−
 
 
−
 
 
  
 
==References==
 
==References==
−
 
 
<references/>
 
<references/>
  
Line 391: Line 343:
  
 
{{author
 
{{author
−
|AuthorID=33173
+
|AuthorID=13331
−
|AuthorFullName=Benoît Camanen
+
|AuthorFullName=Mangor, Karsten
−
|AuthorName=Benoît Camanen}}
+
|AuthorName=Karsten}}
  
−
[[Category:Physical coastal and marine processes]]
+
[[Category:Definitions]]
−
[[Category:Sediment]]
 

Revision as of 14:45, 24 October 2019




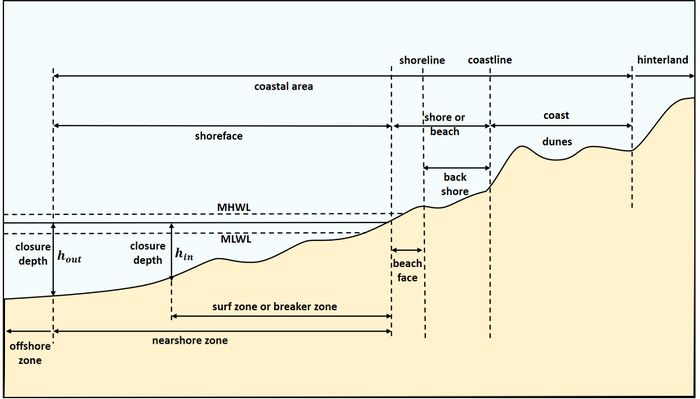
This article gives an overview of terminology frequently used in the Coastal Wiki. Many definitions are derived from Mangor et al. 2017 [1]. Terms related to the coastal profile are illustrated in the figure below.



Fig. 1. Definition of coastal terms, adapted from Shore Protection Manual, 1984.[2]


Accretion or Aggradation

Growth (vertical and/or horizontal) of morphological features (beach, bar, dune, sand bank, tidal flat, salt marsh, tidal channel, etc.) by sedimentation.

Active coastal zone

The active coastal zone (also called active coastal profile) is the cross-shore coastal zone that is highly dynamic by the action of tides, waves and wind. It extends from the closure depth up to a fixed land boundary (rock, cliff, seawall, sea dike). In the case of a dune coast the front dune is part of the active coastal zone. See: Active coastal zone.

Angle of incidence

The angle between the wave propagation direction and the normal to the coastline or the angle between the wave front and the coastline (often denoted [math]\alpha[/math]). When waves enter shallow water, the wave propagation direction tends to become perpendicular to the depth contours, by refraction. See: Shallow-water wave theory, Wave transformation. The deep water angle of incidence is often denoted [math]\alpha_0[/math].

Armouring

  1. Manmade structures such as seawalls, revetments, bulkheads, geotubes, etc. intended to prevent damage of properties situated on the coast;
  2. The natural process of removing fine sediment from the beach or seabed top layer, leaving coarse material behind, thus leading to a more erosion-resistant residual top layer. This process may occur at places where beach or seabed material is a mixture of fine and coarse sediments (so-called graded sediment).

Astronomical tide

See Tide

Avulsion

The sudden abandonment of an existing tidal channel in favour of a newly formed channel. Channel avulsion is a common process in tidal deltas.

Backshore

The part of the beach lying between the foreshore and coastline. The backshore is dry under normal conditions; it is generally without vegetation and often characterised by berms. The backshore is only exposed to waves under extreme events with high tide and storm surge.

Bar

Elongated sand body created by (tidal) currents or by waves . Bars in estuaries and tidal lagoons develop naturally in flow convergence zones, often in relation with channel meandering. Estuarine bars also occur where ebb- and flood-dominated channels meet. Bars that partially block the openings to minor streams and lagoons are mainly due to littoral drift; these bars are generally referred to as spits. Wave action is responsible for the development of breaker bars, beach berms and swash bars. Bars can raise above the high water level, but they are often intratidal or subtidal.

Bathymetry

Mapping of the seafloor depth with respect to the mean water level. The term is also used for the description of seafloor topography or coastal morphology.

Beach

The beach (or shore) zone of unconsolidated material that extends from the mean low water line to the place where there is a marked change in material or physiographic form (e.g. dunefoot), or to the line of permanent vegetation (the effective limit of storm waves and storm surge), i.e. to the coastline. The beach or shore can be divided in the foreshore and the backshore. Often a distinction is made between dissipative and reflective beaches.

Beach berm

A beach berm (or beach ridge or swash bar) is a nearly horizontal shore parallel ridge formed on the beach due to the landward transport of the coarsest fraction of the beach material by the wave uprush. There may be several beach berms and in some cases no berms. Under normal conditions a beach berm is formed on the upper part of the foreshore, and over the backshore during severe events.

Berms can also form on the higher intertidal zone of a beach or a tidal flat; these berms are generally called "swash bars". They may be related to onshore moving breaker bars.

Beach cusps

Regularly spaced shoreline structures (spacing typically between a few meters and a few tens of meters) consisting of small embayments between protruding horns. They are a common feature of reflective beaches. See: Beach Cusps.

Beach face

See Foreshore

Beach fill

The supply of beach sand for the construction of an artificial beach.

Beach park

A beach park is a scheme which consists of new artificial beaches, stabilising coastal structures and filling/reclamation, which in combination provides new recreational facilities. Artificial beaches will be exposed to wave action and will evolve to a stable plan and profile shape.

Bed forms

The seafloor is seldom flat, but generally undulated by the interaction with currents and waves . Undulated bedforms exist over a large range of spatial scales, from centimeters up to kilometers, see: Wave ripples, Wave ripple formation, Sand ridges in shelf seas, Stability models. The smallest bedforms play an important role in the friction exerted by the seabed on water motion, see Boundary layer, Bedforms and roughness, Bed roughness and friction factors in estuaries, Wave ripples, Wave ripple formation.

Bedload

Bedload transport refers to sediment transport by rolling and saltating sediment grains over the seabed. Bedload transport is the dominant sediment transport mode when the flow velocities (currents and wave-orbital velocities) are above the critical velocity for setting bed particles in motion (in the order of 0.2-0.4 m/s for sandy sediments), but insufficient for bringing sediment particles in suspension. Bedload transport occurs for non-cohesive medium-coarse sediments and is associated with the formation of bed ripples and dunes. The migration of these bedforms yields an estimate for the bedload transport. See: Sand transport.

Benthos

Organisms living on or in the seabed, including vegetation.

Boundary layer (turbulent)

The fluid layer where momentum and energy are dissipated as a result of friction exerted by the seafloor or a nearby hard boundary. In the boundary layer, fluid momentum is dissipated through transfer from the large-scale flow pattern in a cascade process to increasingly smaller turbulent flow structures. The large-scale flow profile in the turbulent boundary layer has a logarithmic profile. The thickness of the turbulent boundary layer corresponds to the size of the largest turbulent eddies generated by friction at the seafloor. Because the development of the turbulent boundary layer takes time, the boundary layer thickness for slowly varying currents is much greater than for rapidly varying currents. The boundary layer thickness for steady flow and tidal flow is typically of the order of 10-50% of the water depth, whereas the boundary layer thickness for wind-driven waves is only a few centimeters. Hence, steady flow and tidal flow experience much stronger friction than propagating wind-driven waves. See: Bed forms, Wave ripples.

Breaker zone

The breaker zone (or surf zone) is the part of the shoreface exposed to depth-limited breaking waves, see Fig. 1. The outer limit of the breaker zone (or surf zone) is called the breaker line. However, the instantaneous width of the breaker zone varies with the instantaneous wave conditions and water level. In the general context, the surf zone width is defined in relation to the yearly wave climate defined by the significant wave height [math]H_{s,12h/y}[/math], which is the wave height exceeded 12 hours per year. The surf zone thus corresponds to the zone where waves of height [math]H_{s,12h/y}[/math] break. The surf zone is somewhat narrower than the littoral zone. It is estimated that 80 to 90% of the yearly littoral transport takes place within the breaker or surf zone.

Breaker bar

A submerged shore parallel embankment of sand or gravel built in the breaker zone due to the action of breaking waves and cross-currents. There can be several rows of bars. Breaker bars are very mobile formations, which tend to be in unstable equilibrium with actual wave and tide conditions, which means that they are constantly changing. The overall tendency is that the bars are moving seawards during storm wave conditions and landwards during conditions dominated by smaller waves and swell. At intervals there are gaps in the breaker bars formed by rip currents.

Breakwater

A structure built for reducing wave activity in the waters at the leeside. It can be linked to the shore or it can be positioned offshore. A common type is the detached breakwater. This is a structure approximately parallel to the coast, built inside or outside the surf zone. The main purpose of detached breakwaters is either to protect a harbor entrance or a ship wharf from wave action or to reduce wave activity at the beach. See: Application of breakwaters, Detached breakwaters, Detached shore parallel breakwaters, Floating breakwaters.

Buoyancy

Upward force experienced by a body of lower density (water body of lower salinity, higher temperature, for example) than the surrounding fluid.

Chenier

An accretionary feature consisting of a long, low lying, narrow strip of gravelly sand (typically up to 3 m high and 40 to 400 m wide), often shelly, deposited in the form of wave-built beach ridge on a swampy, deltaic, or alluvial coastal plain of fine sediment.

Closure depth

The depth beyond which no significant longshore or cross-shore transports take place due to littoral transport processes. The closure depth can thus be defined as the depth at the seaward boundary of the littoral zone, see: Closure depth.

Coast

The strip of land that extends from the coastline inland to the first major change in the terrain features, which are not influenced by the coastal processes. The main types of coastal features are dunes, cliffs and low-lying areas, possibly protected by dikes or seawalls.

Coastal area

The land and sea areas bordering the shoreline.

Coastal cell

See Sediment cell

Coastal development

Any activity likely to alter the physical nature of the coastal zone in any way, including construction of buildings and works, the deposit of waste or other material from outfalls, vessels or by other means, the removal of sand, sea shells, natural vegetation, sea grass and other substances, dredging and filling, land reclamation and mining or drilling for minerals, but excluding fishing activities.

Coastal erosion

Distinction must be made between incidental coastal erosion and ongoing coastal erosion.

Coastal hinterland

The land that extends landward of the coast and which is not influenced by coastal processes.

Coastal morphology

Coastal morphology (or coastal geomorphology or morphology) is the science of natural morphodynamic processes, which are responsible for shaping the coastal zone. The meaning of the Greek word "morphè" is form or shape. These natural processes, which involve wind, tides, currents, waves, biota, soil and sea-level changes, interact with the materials from which the coastal zone is built; this interaction is called coastal morphodynamics. Coastal zones around the world are shaped in highly diverse ways. The term coastal morphology is also used for the description of these very diverse coastal forms. See also: Characteristics of sedimentary shores, Classification of coastlines.

Coastal profile

The cross-shore profile of the active coastal zone. See also: Shoreface profile.

Coastal protection

Three different protection/defence definitions are used as follows:

Coastal zone

General, wide planning-oriented characterisation: The interface between land and sea, defined as the part of the land affected by its proximity to the sea (influence of marine processes), and the part of the sea affected by its proximity to the land (influence of terrestrial processes).

Coastal zone management (CZM)

The aim of coastal zone management is to balance the different interests of coastal areas, which are related to: safety, environment, economy, human activities and esthetic and cultural values, see also: Integrated Coastal Zone Management (ICZM) and Some definitions of Integrated Coastal Zone Management (ICZM). Because of this comprehensive scope the term Integrated coastal zone management (ICZM) is more widely used than CZM. The dynamic nature of the coastal zone is a highly challenging aspect of coastal zone management. Coastal engineering (hard or soft measures) and coastal area planning are major instruments for coastal zone management. See: The Integrated approach to Coastal Zone Management (ICZM), Spatial Planning and Integrated Coastal Zone Management, Policy instruments for integrated coastal zone management, Shoreline management.

Coastline

Technically the line that forms the boundary between the coast and the shore, i.e. the foot of the cliff or the foot of the dunes. Commonly, the line that forms the boundary between the land and the water. See also: Classification of coastlines.

Coastline retreat

Landward shift of the coastline caused by a long-term erosional trend or by sea-level rise.

Continental shelf

The continental shelf (or shelf sea) is the continental border which is submerged in relatively shallow sea (water depths typically less than 200 m). The continental shelf extends from the coastline of a continent to a drop-off point called the shelf break. From the break, the shelf descends toward the deep ocean floor in what is called the continental slope. Water motion, water quality and ecosystem of shelf seas are strongly influenced by the adjacent ocean, see Shelf sea exchange with the ocean.

The legal definition of a continental shelf is different than the geographic one. According to the UN Convention on the Law of the Sea, every nation has a continental shelf extending no more than 200 nautical miles from the nation's coastline. See: Legislation for the sea.

Coriolis

The acceleration experienced by a current due to earth rotation, see: Coriolis acceleration.

Creek

A tidal channel that drains a salt marsh.

Deep water

Water too deep for waves to be affected by the seafloor; typically taken as half the wavelength, or greater.

Delta

The fan-shaped mouth of a river or a tidal basin, formed by several distributary channels. They are the result of depositional and erosional processes under the influence of currents, waves and tides. Because of their different morphologies, often a distinction is made between river-dominated deltas, wave-dominated deltas and tide-dominated deltas. See: Morphology of estuaries, Wave-dominated river deltas.

Flood deltas are sedimentary bodies deposited by flood currents. Ebb-tidal deltas are sedimentary bodies deposited by ebb currents. Flood deltas and ebb-tidal deltas are generally present at the inshore and offshore sides (respectively) of tidal inlets of estuaries and tidal lagoons.

Dispersion

  1. The passive dispersal of dissolved substances in the marine or estuarine environment. Dispersion is the overall mixing effect of all hydrodynamic processes including turbulence, flow circulations and gradients in current velocity. See: Seawater intrusion and mixing in estuaries, Transport and dispersion of pollutants, nutrients, tracers in mixed nearshore water, Shelf sea exchange with the ocean.
  2. Wave field transformation due to the dependence of propagation speed on wave frequency.

Dissipative and reflective beaches

Dissipative beaches have typically gentle coastal profiles; they are subjected to energetic short-crested waves, which are strongly damped in the nearshore zone. Dissipative beaches have medium to large intertidal zones which consist of fine (sandy or muddy) sediment. Reflective beaches have typically steep slopes and are subjected to low-energy swell waves. An intertidal zone is almost absent and the beach consists mainly of coarse (sandy or gravelly) sediment. Beach types can be characterised by the so-called ' Dean parameter ' [math]\Omega=H_0/(w_s T_p)[/math], where [math]H_0[/math] is the deep-water wave height, [math]w_s[/math] the mean fall velocity of beach sediment and [math]T_p[/math] the peak spectral wave period. Reflective beaches correspond to [math]\Omega \lt 1[/math] and dissipative beaches to [math]\Omega \gt 6[/math]. See Characteristics of sedimentary shores.

Dunes

  1. The term 'dunes' generally indicates subaerial dunes. These dunes are ridges or moulds of loose, wind-blown sand (fine to medium) forming on the backshore and forming the coastal features at certain locations. Dunes are more or less vegetated. Dunes are active coastal form elements acting as a flexible sand reservoir. At coasts subject to structural coastal erosion they are moving backwards in parallel with shoreline retreat. Dunes act as a kind of flexible natural protection against erosion and flooding, see Dune erosion. If the vegetation is damaged by too much traffic or grazing etc. the integrity of the dunes may be endangered.
  2. The term 'dunes' is also used for subaqueous dunes, which are frequently called sandwaves. Subaqueous dunes are bed forms induced by the interaction of the seabed with currents. Sandy seabeds are often covered with dune fields in regions where the maximum (tidal) current velocity is in the range 0.5-1.5 m/s. Dune spacing (generally more than 10 m and less than 1000 m) depends mainly on water depth. Dunes can reach a height of 10-50% of the water depth; high dunes present a risk for navigation.

Environmental impact assessment (EIA)

A written analysis of the predicted environmental consequences of a proposed development activity, including

  • a description of the avoidable and unavoidable adverse environmental effects (in conjunction with the cumulative effect of other human interventions);
  • a description of alternatives to the activity which might be less harmful to the environment, together with the reasons why such alternatives were rejected;
  • a description of any required irreversible or irretrievable commitments of resources required by the proposed development activity.

Estuary

The transition zone between the riverine and the marine environment. A usual definition is: a semi-enclosed coastal body of water, which has a free connection with the open sea, and within which sea water is measurably diluted with freshwater derived from land drainage. Strong tides intrude in general much further upstream than seawater. From a morphological and sedimentary point of view it is therefore more logical to consider as upstream estuarine boundary the location where tidal discharges become much smaller than river discharges, instead of the seawater intrusion limit. See: Seawater intrusion and mixing in estuaries, Morphology of estuaries.

Estuarine circulation

Residual flow pattern in an estuary driven by density differences between fluvial water and seawater. See: Estuarine circulation, Salt wedge estuaries.

Excavation

See Mining

Fetch

Length in the wind direction of the marine area where water waves are generated by wind.

Friction

Shear stresses generated by the seabed and by flow obstacles, causing loss of fluid momentum. The shear stresses are transmitted to the flow via the turbulent boundary layer. See: Bed forms, Bed roughness and friction factors in estuaries, Bedforms and roughness

Foreshore

Foreshore or (beach face) is the zone between mean low water (MLW) and the seaward beach berm, which is equivalent to the upper limit of wave run-up at high tide, see Fig. 1. The foreshore is the part of the shore/beach which is wet due to the varying tide and wave run-up under normal conditions, i.e., excluding the impact of extreme storm waves and storm surge. This means that the foreshore in morphological terms extends further up on the beach than the intersection between the mean high water (MHW) and the coastal profile (MHW line). However, for practical reasons the administrative upper delineation of the foreshore is often defined as the intersection between the MHW line and the coastal profile, which is identical to the definition of the shoreline.

Graded sediment

A sediment bed composed of a mixture of fine and coarse grained sediment particles.

Gravel beach

Beach built of granular material with a size larger than 1 mm: very coarse sand (>1 mm), gravel (2-4 mm), pebbles (4-64 mm) and cobbles (>64 mm), see Coastal and marine sediments. Beach material often originates from erosion of nearby cliffs or is supplied by gravel rivers draining nearby mountains. Gravel beaches have steep slopes and occur on coasts exposed to strong wave action. Cusp patterns are a common beach feature. See: Gravel Beaches.

Groyne or groin

A straight structure perpendicular to the shoreline. Groynes work by blocking (part of) the littoral drift. They trap/maintain sand on their updrift side and cause erosion on the downdrift side. Groynes can have special shapes and they can be emerged, sloping or submerged, they can be single or in groups, the so-called groyne fields. Groynes are normally built as rubble mound structures, but they can also be constructed in other materials, such as concrete units, timber, etc. See: Groynes, Groynes as shore protection, Deteriorated groynes.

Headland

Land mass with a considerable elevation that borders beaches. Headlands form the boundaries to sediment cells, compartmentalising sand transport along the shore, and reducing sand exchange between adjacent beaches.

Artificial headlands are smooth structures built from the coastline over the beach and some distance out on the shoreface. They work by blocking (part of) the littoral transport. A headland combines the effects of groynes and detached breakwaters and at the same time, minimises some of the disadvantages of groynes and breakwaters – see Modified breakwaters and headlands.

Infragravity waves

Ocean surface waves with a period of typicallly 25-250 s. They arise in particular through non-linear interactions within wave groups. They play an important role in beach dynamics of dissipative coasts because their amplitude increases shoreward, relative to the breaking short waves. See: Infragravity waves.

Internal waves

Waves on the interface of fluid layers with different densities. Internal waves can be very large when the density difference between the fluid layers is small. Breaking of internal waves contributes to mixing of the layers and destruction of the layer structure.

Intertidal zone

Area which is dry at low water (LW) and submerged at high water (HW), where LW and HW refer to mean spring tide. The foreshore, tidal flats and (parts of) salt marshes are intertidal zones.

Jetty

  1. Breakwater protecting a harbour entrance channel from wave action (also called harbour mole);
  2. Structure (often a bridge) connecting an offshore ship mooring to the coast.

Lagoon

Area of relatively shallow water situated in a coastal environment, separated from the open marine conditions by a natural barrier (a sand spit, a barrier island or a coral reef), but with an access to the sea. One may distinguish between microtidal and macrotidal lagoons. Examples of microtidal lagoons are Great South Bay and Pamlico Sound at the US Atlantic coast. Examples of macrotidal lagoons (also called tidal lagoons) are the Wadden Sea at the Dutch-German-Danish North Sea coast and the Bassin d'Arcachon at the French Atlantic coast. Tidal lagoons are distinct from microtidal lagoons by the existence of deep tidal inlets and large tidal flats. See also: Morphology of estuaries.

Littoral cell

See Sediment cell

Littoral drift

Littoral drift or longshore sediment transport is the term used for the longshore transport of non-cohesive sediments, i.e. mainly sand, along the foreshore and the shoreface due to the action of breaking waves and longshore current. The littoral dift is also called longshore sediment transport. Formulas for the longshore sediment transport are given in: Littoral drift and shoreline modelling; see also Coastal Hydrodynamics And Transport Processes.

Littoral zone

See Shoreface

Longshore current

The longshore current or nearshore current is the dominating current in the nearshore zone and is running parallel to the shore. The longshore current is generated by the shore-parallel component of the stresses associated with the breaking process for obliquely incoming waves , the so-called radiation stresses, and by the surplus water which is carried across the breaker zone towards the coastline. See: Shallow-water wave theory.

Longshore sediment transport

See Littoral drift

Management unit (MU)

A management unit is a coastal stretch with coherent characteristics in terms of both natural coastal processes and land use. The MU is used as boundary for Shoreline Master Plans.

Marine regression

Coastal extension due to a falling relative sea level.

Meandering

Natural propensity of a flow to scour the outer bend of a channel. When a channel meander becomes very large a cutoff channel (a so-called channel chute) is often formed, leading to avulsion of the meander.

Mining

Mining (or excavation) is the mechanical removal of consolidated soil or unconsolidated material (aggregates like sand, gravel, shells) from seabed, beach or dunes.

Mitigation

Action (or series of actions) aimed at (partly) neutralising the adverse impacts of past or planned human interventions.

Model

Physical or mathematical representation of nature, for studying or predicting coastal behaviour; see Modelling coastal hydrodynamics.

  • Physical models. These models copy salient features of nature at a reduced scale in a laboratory setting. Scale effects are an important issue for the translation of observed model results to the natural scale. Major scale effects generally arise for the representation of phenomena influenced by friction, by sediment transport (including sediment erosion and deposition) and by biota.
  • Mathematical models. These models solve in one way or another the governing hydrodynamic (and/or morphodynamic) equations . They exist in many different types, see for example Estuarine morphological modelling. Most common types are: Analytical models, Numerical process-based models, Behaviour-based models, Stochastic models, Data-driven models, Particle-based models and Cellular models. Analytical models are based on explicit solutions of the governing equations, which are strongly simplified to retain only those features which are most pertinent to the studied phenomena. Numerical process-based models describe nature on a discretised grid, retaining all physical features relevant for a reliable and accurate representation of the studied phenomena; the governing equations are solved numerically for successive discrete time steps, see Process-based modelling, Process-based morphological models. Behaviour-based models (also called Aggregate-scale models) consider the coastal system as an assembly of interacting subsystems and solve the governing equations numerically for the interactions at system level, whereas empirical relationships are used for representing the dynamics at subscale levels; see: Behaviour-based models. Stochastic models are process-based models which use probability distributions for certain input data for taking into account natural fluctuations (wave climate, river discharge, for example) or uncertainty (sea-level projections, model parameters, for example); see Stochastic and fractal methods in coastal morphodynamics. Data-driven models are used to make moving forecasts by integrating observed data of the recent history to calibrate uncertain model parameters or uncertain model input data, see: Reduction of uncertainties through Data Model Integration (DMI). Particle-based models describe numerically the motion of discrete fluid parcels taking into account their mutual interaction according to the laws of physics; in the most popular method (called Smoothed-particle Hydrodynamics (SPH)) the fluid is divided into a set of discrete moving parcels with properties which are smoothed over the parcel size according to a prescribed smoothing function. Cellular models divide the coastal system in fixed discrete cells which behave in a prescribed way according to the evolution of neighbouring cells, taking into account physical conservation laws.
  • Hybrid models combine physical and numerical models.

Morphology

Morphology is the study of the form of things. In the coastal context, morphology or geomorphology is generally used for designating the coastal bathymetry, including its sedimentary composition and structure. See also Coastal morphology.

Morphodynamics

See Coastal morphology.

Mud

Fine cohesive sediment deposit containing a high fraction (≥20%) of clay minerals. Fine sedimentary particles, consisting of clay minerals, but also other particles (silt, fine sand, organic matter), can be glued together by large organic molecules (extracellular polymeric substances, EPS) into large mud flocs. These flocs, with a diameter of 0.1-1 mm, settle much faster than the individual particles and can form a colloidal suspension on the seabed. This so-called fluid mud layer can move along the seabed (driven by pressure gradients at the interface, by flow entrainment or by bed slope effect) and be a major cause of harbor siltation. After consolidation, which is often a lengthy process, a mud bed can become highly resistant to erosion by currents. See: Dynamics of mud transport , Sediment deposition and erosion processes, Characteristics of muddy coasts.

Nearshore zone

The zone extending seaward from the low water line well beyond the breaker zone; it defines the area influenced by the nearshore currents. The nearshore zone extends somewhat further seaward than the littoral zone.

Nourishment

Nourishment (or sand nourishment) is a method to neutralize the effect of coastal erosion by maintaining the sand volume of the active coastal zone. Sand is extracted (generally by dredging) from nearby sources and applied to the beach, the shoreface or the dunes. The costs highly depend on the location of available sand sources, which should be situated outside (seaward of) the active coastal zone. Dune nourishment is usually meant for safety against flooding, beach nourishment for restoration of the beach and shoreface nourishment for stabilizing the shoreline. See: Shore nourishment, Artificial nourishment.

Overwash

Wave uprush over a natural or artificial coastal barrier. The term overwash is also used for the resulting sand deposit at the leeside of the barrier.

Offshore zone

The offshore zone is not clearly delimited. In relation to beach terminology, the offshore zone is often defined as the zone off the nearshore zone.

Progradation

Coastal extension into the sea due to natural aggradation. Coastal progradation occurs specifically where rivers supply large amounts of sediment.

Propagation speed

The speed at which a wave propagates. The speed [math]c[/math] of a wave propagating without frictional losses in shallow water is proportional to the square root of the water depth [math]h[/math] (formula: [math]c=\sqrt{gh}[/math]). A wave group propagates at a smaller speed [math]c_g[/math] than the constituent short waves. Wave energy propagates at the speed of the wave group. See: Shallow-water wave theory.

Reclamation

The transformation of areas which were formerly part of the marine or estuarine domain into non-floodable land.

Reef

A ridge of material at or near the surface of the ocean. Natural reefs are made of rocks or the skeletons of small animals called corals. Reefs can also be created artificially for several reasons:

  • Protect coastlines from erosion;
  • Promote sea life for recreation and aquaculture;
  • Create a wave pattern that promotes the sport of surfing.

See: Natural barriers, Artificial reefs.

Reflective beaches

See Dissipative and reflective beaches

Refraction

The propensity of waves to align the wave front in shallow water with the depth contour, according to Snell's law. Also: Change of wave propagation direction due to the interaction with currents.

Rip current

A local current directed away from the shore, bringing the surplus water carried over breaker bars back into deeper water. Rip currents may occur at certain intervals along the shoreline as a result of the interaction between breaking waves and the nearshore bathymetry, see: Rhythmic shoreline features, Stability models. The rip opening in the breaker bars will often form the lowest section of the coastal profile; a local setback in the shoreline is often seen opposite the rip opening. The rip opening travels slowly downstream. Rip currents are dangerous for swimmers.

Revetment

A revetment is a facing of stone, concrete units or slabs, etc., built to protect a scarp, the foot of a cliff or a dune, a dike or a seawall against erosion by wave action, storm surge and currents. This definition is very similar to the definition of a seawall, however a revetment does not protect against flooding. Furthermore, a revetment is often a supplement to other types of protection such as seawalls and dikes. See Revetments, Seawalls and revetments.

Runnel

Small beach channel draining a tidal pool left on the beach after high water.

Salt marsh

A densely vegetated coastal ecosystem situated in the upper coastal intertidal zone between land and intertidal mudflats, or bordering directly open saltwater or brackish water if mudflats are absent. Salt marshes are sometimes referred to as schorre or kwelder. The soil may be composed of deep mud and peat. Salt marshes usually form in areas that are well sheltered, such as lagoons and estuaries where fine sediments can be deposited. They also form behind spits and artificial sea defences where tidal waters can flow gently and deposit fine sediments. See also: Salt marshes.

Sand bank

Popular term for large bars and ridges in tidal waters, especially in relation to navigation hindrance.

Sand nourishment

See Nourishment

Sand spit

See Spit

Sand wave

  1. A subaqueous dune;
  2. A shoreline undulation with a wavelength in the range of a few hundred meters to a few kilometers, see: Rhythmic shoreline features.

Sea-level rise

The so-called greenhouse effect or global warming causes a rise of the mean sea level, which will have a great impact on long-term coastal morphology, see Sea level rise. The long-term gradual sea-level rise will cause a general coastline retreat and an increased flooding risk depending on local conditions. Instead of the absolute rise of the mean sea level it is more relevant to consider the relative sea-level rise: the rise relative to vertical land motions that can be positive (uplift) or negative (subsidence). An estimate of coastline retreat due to relative sea-level rise can be derived from the so-called Bruun rule, which is valid under certain rather restrictive conditions, see: Bruun rule.

Sediment

Fine-grained loose particles such as gravel, sand, mud. These sediments are produced by chemical or physical weathering of rocks, by seabed erosion and by soil erosion in river basins. They are called clastic sediments and consist of quartz, feldspar, mica and clay minerals. Other particles have a biotic origin, for example shell debris, peat, detritus, fecal pellets and plankton. Sediment particles have widely different grainsizes: clay (< 0.002 mm), silt (0.01-0.02 mm), sand (0.1-2 mm), gravel (2-5 mm). The density is of the order of 2.65 times the density of water. Sand or gravel beds occur in zones with strong (tidal) currents and strong wave activity, whereas fine sand, silt and mud cover the seabed in sheltered zones where currents and wave activity are weak. See: Coastal and marine sediments, Sediment deposition and erosion processes, Gravel Beaches.

Sediment cell

A sediment cell (or littoral cell or coastal cell) is a coastal compartment that contains a closed cycle of sedimentation including sources, transport paths, and sinks. The cell boundaries (often corresponding to headlands or jetties) delineate the geographical area within which the budget of sediment is balanced, providing the framework for the quantitative analysis of coastal erosion and accretion.

Sediment transport

The capacity of currents and waves to move sediments. Sediment transport is a crucial link in the interaction between coastal morphological evolution and waves, currents and tides. Sedimentation is related to convergence of sediment transport and erosion to divergence of sediment transport. Sediment transport takes place in several ways: Suspended-load transport, Bedload transport and Fluid mud motion. Suspended-load transport is the transport of sedimentary particles that are suspended in the fluid. Bedload transport is the transport of sedimentary particles that are rolling or leaping along the seabed. Fluid mud transport is the motion of a fluid mud layer along the seabed. Formulas for bedload transport are based on empirical relationships involving characteristics of sediment, currents and waves. See: Sediment transport formulas for the coastal environment, Sand transport.

Seiche

Oscillation of a semi-enclosed water body caused by incoming long-period waves (periods typically in the range 200-2000 s). Seiches can be strongly amplified in harbour basins if the period is close to the harbour resonance period, causing damage to ships and moorings.

Setback area

A strip along the coastal zone where certain development activities are prohibited or significantly restricted. See: Setback area.

Sheet-flow

Sheet-flow sediment transport refers to transport of sandy sediments as a fluidized thin surface layer (thickness of ten to several tens grain diameters). This type of sediment transport occurs under strong wave action (wave orbital velocity greater than 1 m/s), where bed ripples are flattened out. In the sheet-flow layer, continuous contacts between sand grains create an intergranular stress. This stress decreases the velocity in the sheet-flow layer to about one half the velocity in the top layer. The sediment concentration in the sheet-flow layer is in the order of 100 to 1000 kg/m3. See: Sediment transport formulas for the coastal environment.

Shelf sea

See Continental shelf.

Shoaling

Amplification of incident waves in the nearshore zone before breaking. Amplification is due to (approximate) continuity of the wave energy flux [math]F=c_g E[/math] seaward of the breaker zone, where [math]E[/math] is the wave energy and [math]c_g[/math] the wave group propagation speed. The landward decrease of [math]c_g[/math] results in a landward increase of [math]E[/math], thus in a landward increase of wave height [math]H[/math]. See: Shallow-water wave theory.

Shore protection

See Coastal protection.

Shoreface

The shoreface (or littoral zone) is part of the active coastal zone, situated seaward of the low water line. This zone extends seaward from the foreshore to some distance beyond the breaker zone. The littoral zone is the zone in which littoral morphodynamic processes take place, related mainly to longshore sediment transport and cross-shore sediment transport. The width of the instantaneous littoral zone varies dependent of the wave conditions. In the general context, the littoral zone is defined as the zone corresponding to the yearly wave climate. The width of the littoral zone can thus be defined as the width of the sediment transport zone for the significant wave height, which is exceeded 12 hours per year, [math]H_{s,12h/y}[/math].

Shoreline

The intersection between the mean high water line and the shore. The line delineating the shoreline on Nautical Charts (Sea Maps) approximates this Mean High Water Line. The shoreline is not easy to identify in the nature in contrast to the coastline, which is based on a clear morphological shift between the shore and the coast.

Shoreline management

The act of dealing – in a planned way – with actual and potential coastal erosion and its relation to planned or existing development activities on the coast, see Shoreline management. The objectives of Shoreline Management are:

  • To ensure the development activities in the coastal area follow an overall land use plan and a general environmental policy;
  • To ensure the development activities in the coastal area do not cause to or aggravate erosion;
  • To ensure that development activities do not occur in sensitive areas;
  • To ensure that erosion control techniques are cost-effective and socially and environmentally acceptable.

Shoreline management is typically based on coastal sediment cells.

Siltation

Accumulation of fine sediments (sand, silt, mud) in channels, harbors and fairways. See: Siltation in harbors and fairways, Dynamics of mud transport , Sediment deposition and erosion processes, Sediment transport formulas for the coastal environment.

Slack tide

Tidal phase at which the current turns from flood to ebb (high-water slack tide) or from ebb to flood (low-water slack tide).

Shore

See Beach

Spit

A spit (or sand spit) is an accretionary feature formed by littoral drift, consisting of a long narrow accumulation of sand or gravel, lying generally in line with the coast, with one end attached to the land and the other projecting into the sea or across the mouth of an estuary or lagoon. During dry periods, a spit can develop into a barrier that temporarily blocks the mouth of a lagoon or a small river.

Storm surge

The rise in water-level on an open coast as a result of the combined impact of the wind stress on the water surface, the atmospheric pressure reduction and local topographic features. The storm surge does not include the effect of the astronomical tide. The storm at a location is in first approximation inversely proportional with the water depth in the offshore zone. This implies that shores out to deep oceans will only be exposed to relatively small surges whereas shores out to shallow seas can be exposed to high surges. See: Extreme storms.

Stratification

Less dense water layer overlying a water layer of higher density (related to higher salinity, lower temperature or higher suspended sediment concentration). Density differences in the vertical inhibit turbulent mixing, which causes the interface of the layer to be sharpened. See: Salt wedge estuaries.

Subsidence

Downward motion of the land surface. It is most often related to soil compaction (underground material movement) caused by the removal of water, oil, natural gas, or mineral resources out of the ground by drainage, pumping, fracking, or mining activities. Subsidence can also be caused by natural events such as earthquakes, glacial isostatic adjustment, erosion, sinkhole formation, sediment loading by river deposites, and adding water to fine soils deposited by wind (a natural process known as loess deposits).

Surf beat

Oscillation of the wave set-up on the foreshore. The oscillation is related to the breaking of wave groups in the surf zone. See: Shallow-water wave theory.

Surf zone

See Breaker zone.

Swash

Wave propagation on the beach, consisting of a decelerating onshore phase (swash or uprush) and an accelerating offshore phase (backwash or downrush). On dissipative coasts swash processes are dominated by infragravity waves. See: Swash zone dynamics.

Swash bar

See Beach berm

Tidal bore

Breaking tidal flood wave. Tidal bores occur in shallow funnel-shaped estuaries with a large tidal range (generally more than 6 m).

Tidal channel

Seabed incision concentrating the main tidal flow. Tidal channels form naturally in sedimentary environments where tide-induced water motion is stronger than wave-induced water motion.

Tidal creek

Drainage channel of a salt marsh.

Tidal flat

Shallow, sandy or muddy part of the foreshore, which is covered and uncovered by the rise and fall of the tide. Muddy tidal flats are also called mud flats or slikke. As a rule of thumb, a tidal flat normally develops when the relative tidal range RTR, defined as the ratio between the mean spring tidal range and the annual average significant wave height [math]H_s[/math], is higher than 15.

Tidal inlet

The entrance to estuaries on sandy shores that have formed where sand barriers or spits enclose bays. They comprise a flood and ebb tidal delta, and a deep narrow throat through which strong currents flow.

Tidal prism

Volume of water flowing during flood through a tidal inlet, or through a certain section of an estuary or a tidal lagoon.

Tidal range

Water level difference between high water and low water, i.e. twice the tidal amplitude. The tidal range changes from tide to tide depending on the positions of moon and sun relative to the earth; the most important change is the fortnightly variation from spring tide to neap tide.

Tidal ridge

Sand ridge with a length of several tens of kilometers and height of a few tens of meters, produced by tidal currents on a shelf sea. Sand ridge fields consist of a number of tidal ridges with a spacing of the order of 5 km. See: Sand ridges in shelf seas.

Tidal wave

The wave associated with tidal motion. The term "tidal wave" is also frequently used as a popular expression for an unusually high and destructive water level along a shore, thus including the combined effect of astronomical and meteorological surges.

Tide

The tide (more precisely, the astronomical tide) is generated by the rotation of the earth in combination with the varying gravitational impact on the ocean of the sun, the moon and the planets. These phenomena cause predictable and regular oscillations in the water level, which is referred to as the tide. The astronomical tide at a specific location can be predicted and is published in Tidal Tables. See: Ocean and shelf tides, Tidal motion in shelf seas. The term 'tide' is sometimes used for the combined effect of astronomical tide and wind-driven set-up or set-down of the sea level (including storm surges).

Transgression

Flooding of land by the sea related to relative sea-level rise. Transgression implies coastline retreat.

Tsunami

Wave (or group of waves) generated by a subsea earthquake. Tsunamis propagate very fast over the ocean with very few energy loss due to the great ocean depth (see: propagation speed). In nearshore waters the amplitude increases dramatically (up to a factor 10) due to shoaling.

Turbidity maximum

Convergence zone of suspended sediment transport in an estuary, where turbidity levels are high due to high suspended sediment concentrations. Upstream (landward) transport of fine suspended sediment in an estuary is possible due to estuarine circulation and tidal asymmetry (maximum flood current stronger than maximum ebb current). This produces a maximum in the suspended sediment concentration just downstream of the zone where the influence of river discharge on sediment transport becomes dominant. Fine sediments in the turbidity maximum zone settle to the bed in periods where currents are small (slack tide, neap tide), which may result in the formation of fluid mud layers. High turbidity often causes oxygen depletion and mortality of estuarine organisms. It also enhances sedimentation of tidal flats and harbours. See: Dynamics of mud transport.

Turbulence

Irregular flow pattern of individual fluid parcels related to small-scale flow instability, see Turbulent boundary layer. Turbulence plays a major role in mixing processes and in energy dissipation. See: Transport and dispersion of pollutants, nutrients, tracers in mixed nearshore water, Currents and turbulence by acoustic methods.

Wave

The term "wave" designates in most cases surface water waves generated by wind (other types of waves are explicitly referred to as tidal wave, tsunami wave, etc.). A wave field is generally a superposition of waves of different height, period and direction that can be described by a wave spectrum. A unidirectional wave field is often characterised by the significant wave height [math]H_s[/math] (representing approximately the mean wave height of the highest third of the waves) and the spectral peak period [math]T_p[/math] (wave period with the highest energy). See: Statistical description of wave parameters. Coasts situated on the open ocean are mainly subjected to long-period swell waves, which are generated far away at the ocean and propagate to the coast with minor energy losses. Coasts situated on inland seas are mainly subjected to locally generated short-crested waves, also called "sea", see Waves.

Wave breaking

Waves start breaking (by spilling or plunging) when entering shallow water, where the depth is smaller than one or two times the wave height. Waves may reform in the surf zone, but remain depth-limited by spilling or by plunging a second time, until final collapse and uprush on the beach. See: Shallow-water wave theory.

Wave energy

Energy carried by waves when propagating. The wave energy [math]E[/math] is proportional to the square of the wave height [math]H[/math] (formula: [math]E=g \rho H^2 / 8[/math]).

Wave group

Incident waves generally arrive in groups, corresponding to the superposition of short-wave trains with slightly differing wave lengths and frequencies. Wave groups generate infragravity waves with the same group wavelength and period, by non-linear interaction. Wave groups also cause surf beat. See: Shallow-water wave theory, Infragravity waves.

Wave height

The water level difference between wave trough and wave crest, or twice the wave amplitude.

Wave run-up

The sum of swash and wave set-up. Wave run-up is an important factor in the design of coastal protection structures and is a dominant process leading to the erosion of coastal dunes.

Wave set-up

Water level elevation at the foreshore related to wave breaking in the surf zone. Wave set-up is proportional to the wave height at the breaker line. As a rule of thumb, wave set-up is of the order of 20% of the offshore significant wave height. See: Shallow-water wave theory.


Related articles

Coastal hydrodynamic and morphodynamic processes and engineering

References

  1. ↑ Mangor, K., Drønen, N. K., Kaergaard, K.H. and Kristensen, N.E. 2017. Shoreline management guidelines. DHI https://www.dhigroup.com/marine-water/ebook-shoreline-management-guidelines
  2. ↑ Coastal engineering Research Center, Department of the Army, Waterways Experiment Station, 1984. "Shore protection manual".



The main author of this article is Mangor, Karsten
Please note that others may also have edited the contents of this article.
Citation: Mangor, Karsten (2019): Definitions of coastal terms. Available from http://www.coastalwiki.org/wiki/Definitions_of_coastal_terms [accessed on 31-10-2024]
Retrieved from "https://www.coastalwiki.org/w/index.php?title=Definitions_of_coastal_terms&oldid=76034"